相関分析とは?
相関分析とは、要素間の関係性を知るための分析手法です。
相関分析を行うと、手元のデータにある変数間の関連性の強さと方向を知ることができます。
相関分析はどんな時に使われているか
小売店や飲食店で気温と売上の関係性を知りたい時など、2つ以上の変数間の関係性を知りたい時によく使われる分析手法の1つです。
その他にも
• マーケティング担当者が広告費と売上の関係、価格と購入意欲の関係性を調べたい
• 商品開発担当者が商品の特徴(価格、デザインなど)と顧客満足度の関係性を見ることで改良点を見つけたい
• 製薬開発者が薬の投与量と治療効果の関係性を知りたい
• 学生の勉強時間と試験成績、教師の経験年数と生徒のパフォーマンスの関係性を知りたい
など、多くの人に様々なシーンで使われています。
相関関係と相関係数を理解する
相関関係とは?
相関関係とは、2つ以上の変数がどのような関係性を持っているかを示す概念です。
具体的には、「一方の変数が変化すると、もう一方の変数がどう変化するか」を表します。
• 正の相関(正の関係)
一方の変数が増加すると、もう一方の変数も増加する関係。
例: 気温が上がるとアイスクリームの売上が増える。
• 負の相関(負の関係)
一方の変数が増加すると、もう一方の変数が減少する関係。
例: 年齢が上がると運動能力が下がる。
• 相関なし(関係がない)
2つの変数間に特定のパターンや関係性が見られない。
例: 髪の長さと試験の得点。
相関係数とは?
相関係数は、2つの変数間の相関関係の強さと方向を数値で表したものです。
相関係数にはいくつか種類がありますが、最も一般的なのはピアソンの相関係数です。
ピアソンの相関係数
• 記号: r
• 値の範囲: -1 ~ +1
• 数式:
相関係数の解釈
• r = +1 : 完全な正の相関(直線的に強い正の関係)
• r = -1 : 完全な負の相関(直線的に強い負の関係)
• r = 0 : 相関がない(2つの変数に直線的な関係が見られない)
• 0 < r < 1 : 正の相関(値が1に近いほど強い正の関係)
• -1 < r < 0 : 負の相関(値が-1に近いほど強い負の関係)
相関係数の目安
• |r| > 0.7 : 強い相関
• 0.3 < |r| < 0.7 : 中程度の相関
• |r| < 0.3 : 弱い相関
相関関係の注意点
1. 相関は因果を示さない
• 相関があっても、一方の変数がもう一方を「引き起こしている」とは限りません。
例: 「アイスクリームの売上」と「水難事故の発生件数」に相関があっても、両者は気温という共通要因が関係しています。
2. 非線形の関係は検出できない
• ピアソンの相関係数は直線的な関係を測るため、非線形(例: 曲線的な関 係)は検出できません。
3. 外れ値の影響
• 外れ値があると相関係数が大きく影響を受ける可能性があります。
相関分析の実践
それでは早速実際にExploratoryを用いて相関分析を実行してみましょう。
必要なデータの形式
相関分析には、1行が1観測対象となっているデータが必要です。また、また、変数の列には数値型の列のみが選択できます。
そこで、今回はサンプルデータとして、小売店舗売上データを使用します。このデータは、1行が1日の売上データを表していて、列には売上金額や来店客数、気温などがあります。
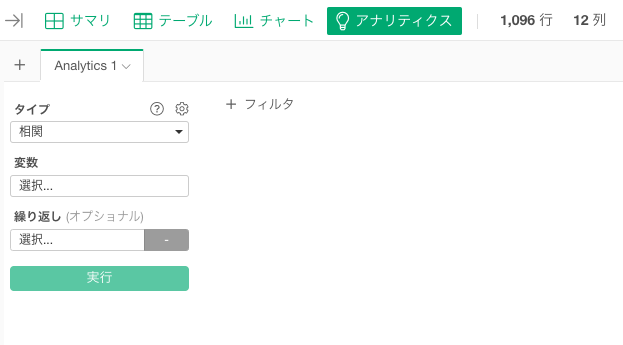
相関分析を実行する
アナリティクスビューを開き、タイプに「相関分析」を選択します。
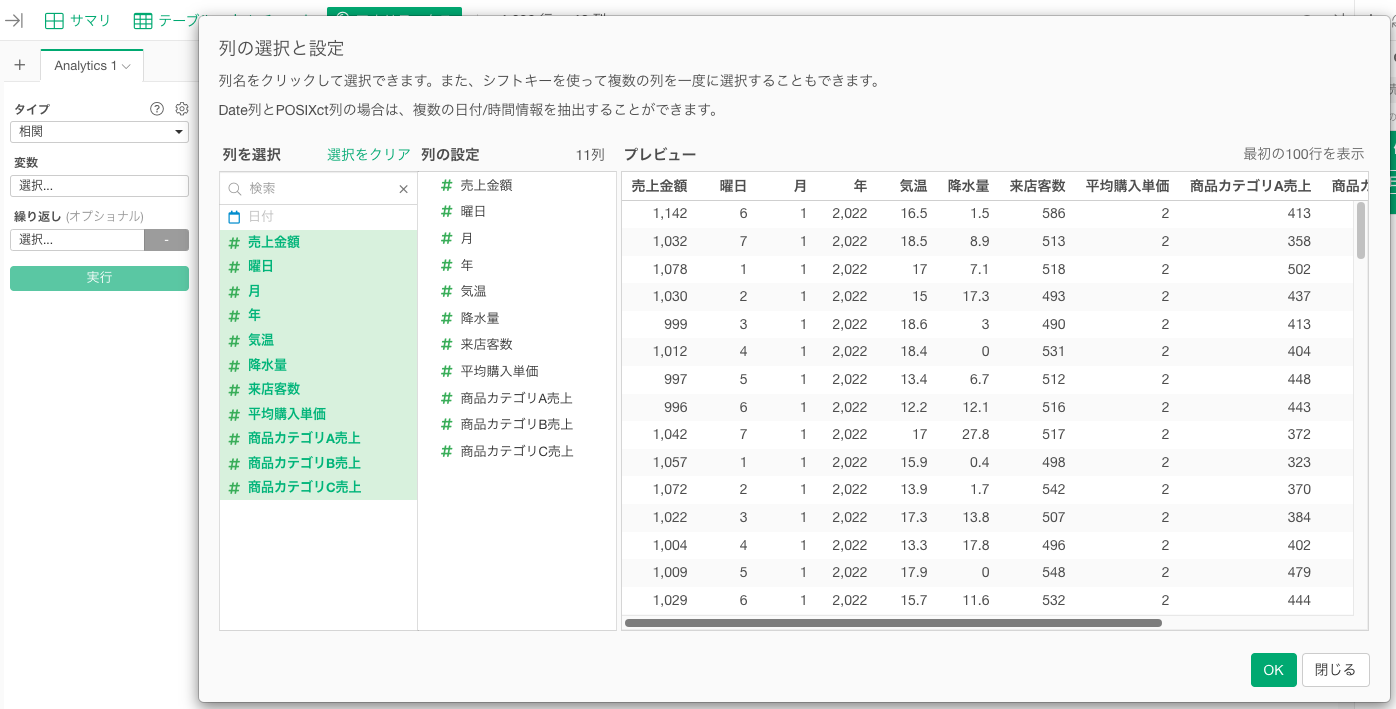
変数の列をクリックして、相関分析に使用する列を選択します。シフトキーを押すことで、複数の列を一気に選択できます。
列の指定が完了したら実行することで、因子分析の結果が表示されます。
結果の解釈
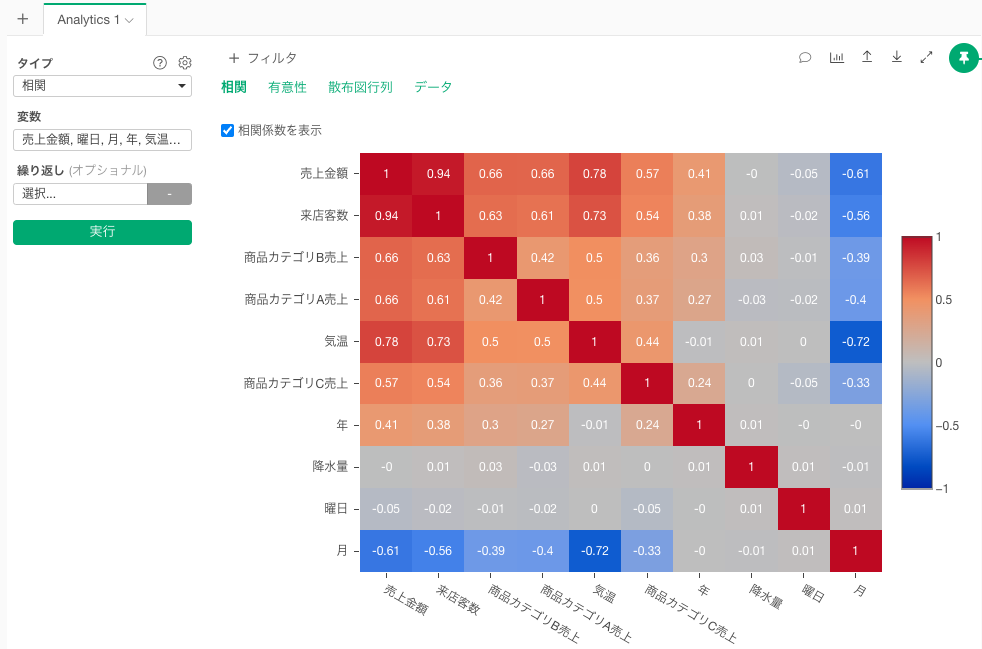
相関
相関のタブでは、それぞれの変数間の相関関係を可視化したチャートが表示されます。
数字はそれぞれの変数間の相関係数を、色は相関の強さを表します。変数間にプラスの相関が強いと数字は1に、色は濃い赤に近づき、マイナスの相関が強いと数字は-1に、色は青に近づいていきます。
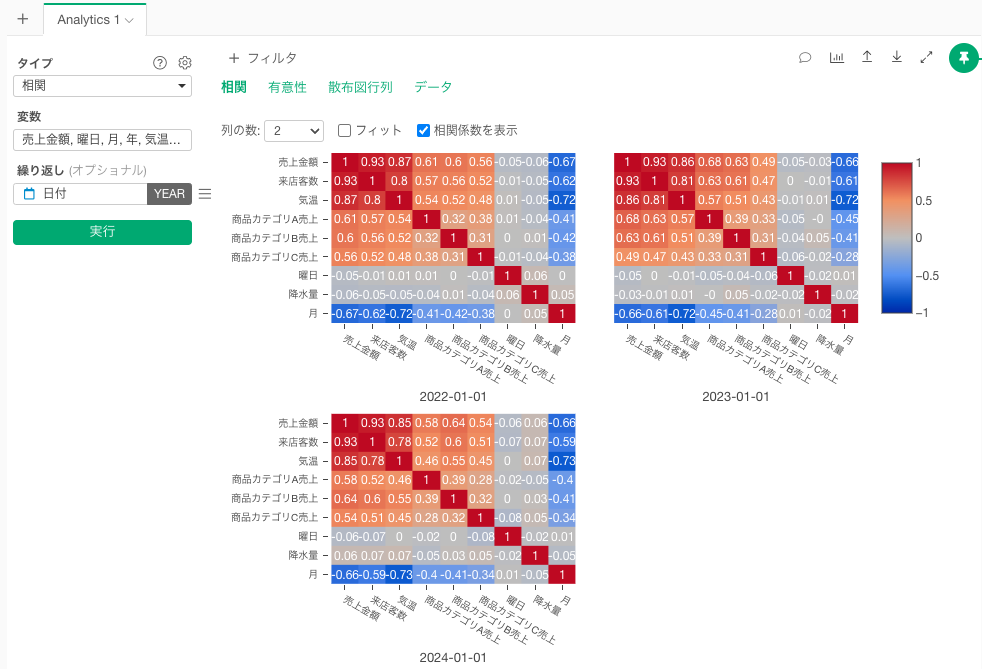
また、「繰り返し」に列を割り当て、「日付」を選択して相関分析を実行すると、時系列で相関の強さの変化を確認することができます。
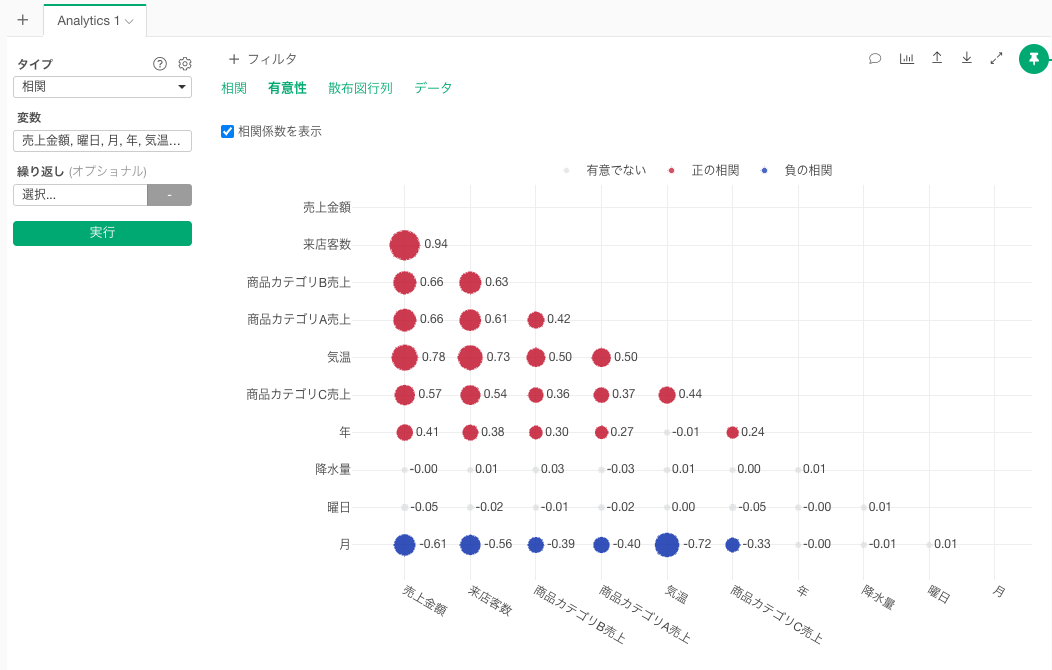
有意性
有意性のタブでは、変数間の相関の強さ数値と円の大きさで、相関の方向を色で表しており、有意でない相関は色(グレー)で確認できます。
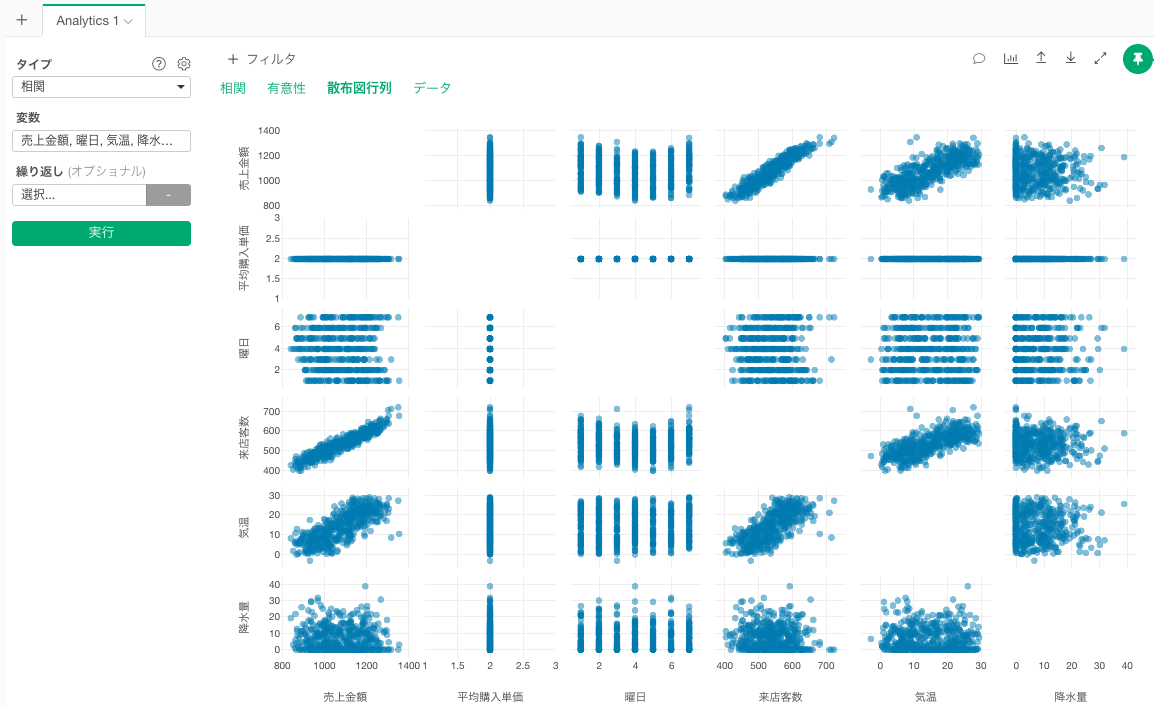
散布図行列
散布図行列のタブでは、変数の組み合わせごとに観測値が散布図の形で表示されます。これにより変数間の相関関係の強さと方向を視覚的に確認することができます。
散布図が左下から右上に連なるほど正の相関が強く、左上から右下に連なるほど負の相関が強いことを意味しています。
来店客数や気温の高さが正の相関が強いことが見出せます。
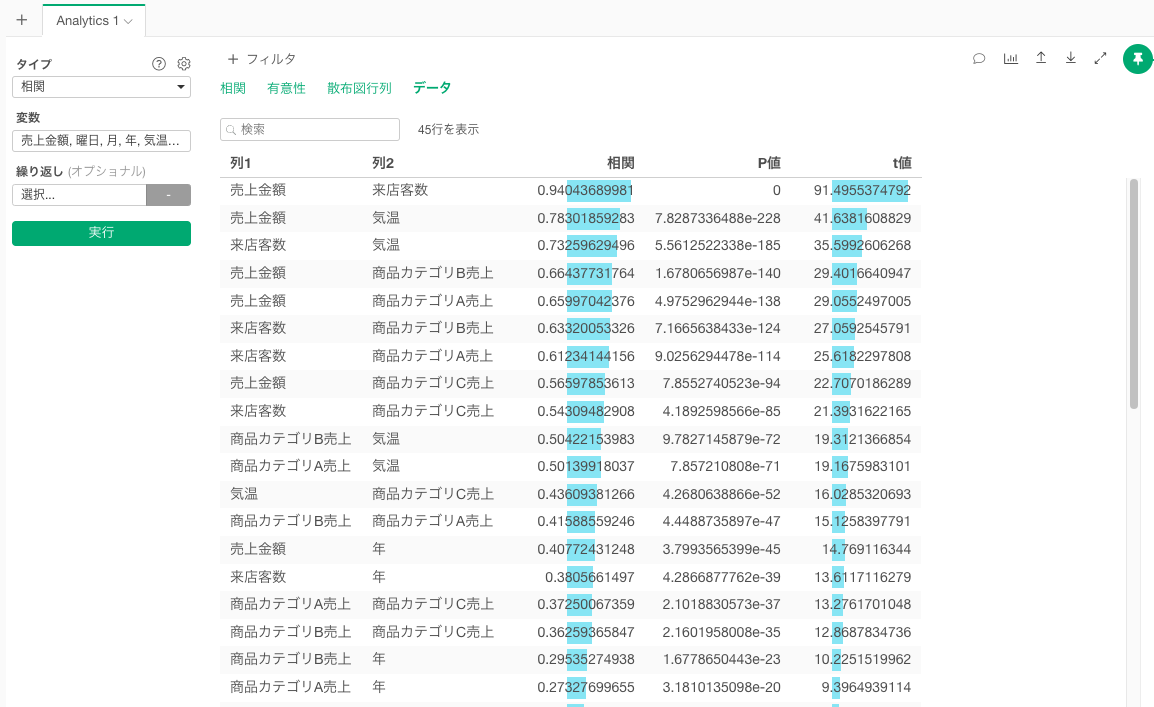
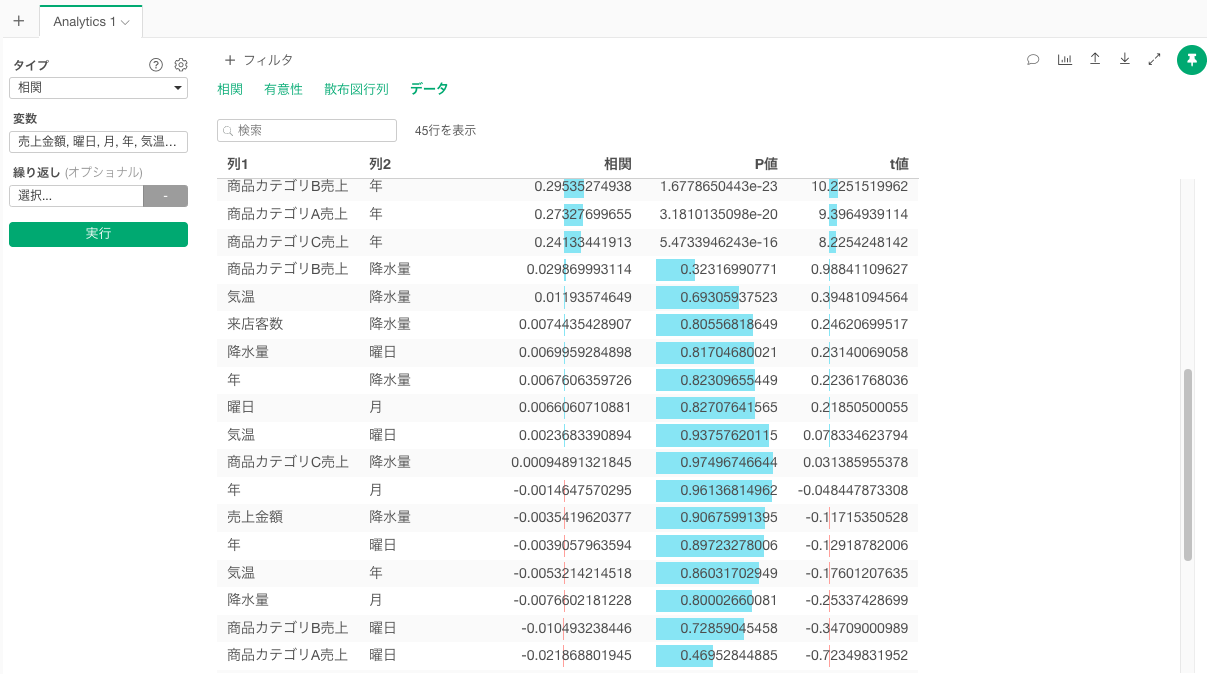
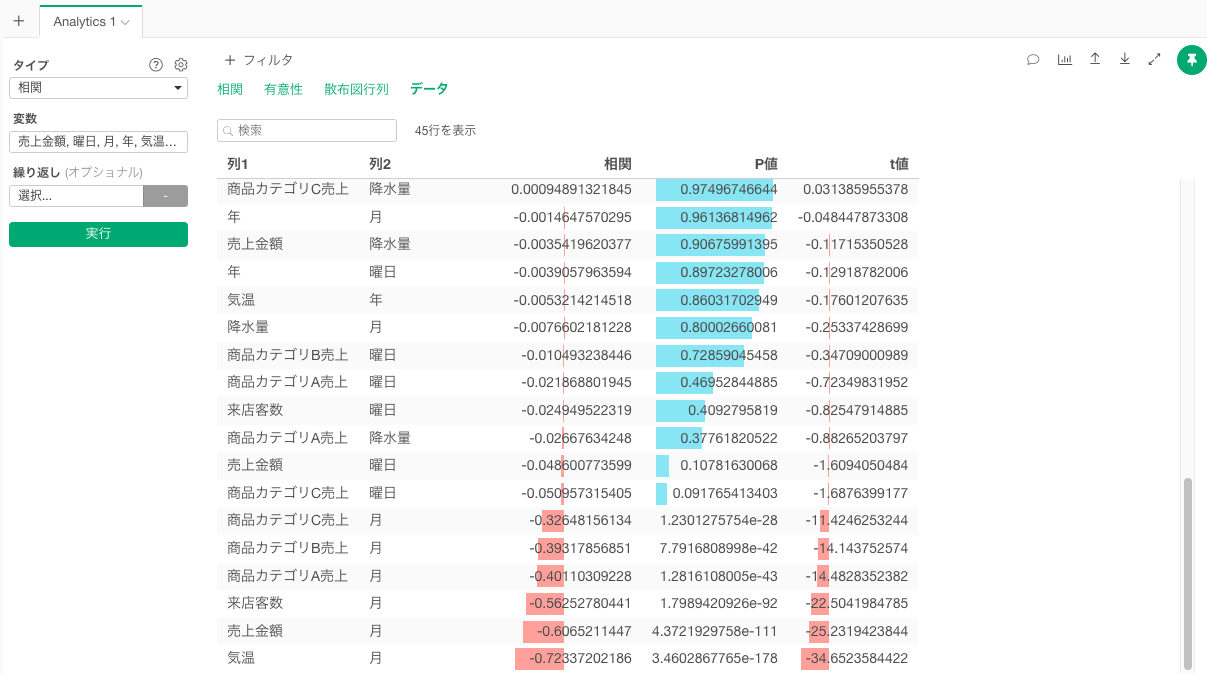
データ
データタブでは、それぞれの変数間の相関関係の強さとP値、t値が確認できます。
eはネイピア数を表しており、P値が0.05を下回っていれば相関係数は有意ではないことを意味します。