線形回帰分析とは?
線形回帰分析はある変数(データ)を別の変数(データ)で説明・予測するための適切なモデルを、観測データから構成するデータ解析法の総称です。
線形回帰分析を行うと、手元のデータから未来のデータを予測したり、説明変数が目的変数に与える影響の大きさを説明することができます。
線形回帰分析はどんな時に使われているか
・マーケティング担当者が広告費が本当に売上アップに影響しているのか、どのくらい影響しいるのか知りたい
・小売店の店長が商品の売上の変化に気温が影響しているのか、どのくらい影響しているのか知りたい
・不動産を購入する企業の担当者が、部屋の広さや築年数、立地条件をもとにどのくらいの価格で売れそうか予測したい
・事業責任者が広告費や商品の価格を元に来月の売上を予測したい
・学生の勉強時間や授業出席率がテストの得点に影響するのか、どのくらい影響するのか知りたい
・年齢や体重、血圧が病気のリスクに影響するのか、どう影響するのか知りたい
など、様々な業界で多くの人に使われています。
線形回帰分析の種類
1. 単回帰分析
• 説明変数が1つの場合の回帰分析。

• 例: 広告費(説明変数)が売上(目的変数)に与える影響を調べる。
2. 重回帰分析
• 説明変数が複数ある場合の回帰分析。

• 例: 広告費、従業員数、プロモーション回数が売上に与える影響を調べる。
例題:線形回帰分析を用いた広告戦略の検証
線形回帰分析を用いた分析をRを用いて具体的にを見ていきます。
今回は売上とメディア別広告費のデータセットを使います。
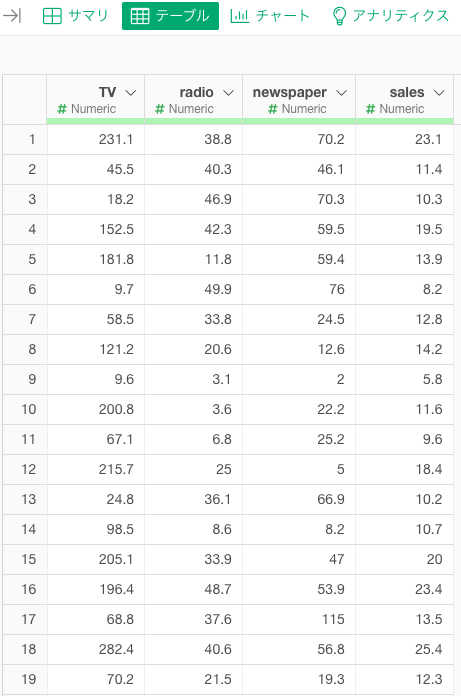
このデータセットは1行が1つの市場におけるsある商品のales(売上)と広告費の内訳を表しています。全部で200行あるので、今回は200の異なる市場における、ある商品のsalesと広告宣伝費(千ドル単位)をまとめたデータということになります。
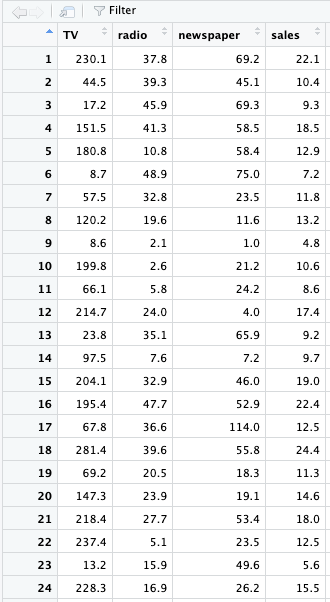
TV:テレビにおける宣伝費
radio:ラジオにおける宣伝費
newspaper:新聞における宣伝費
sales:ある商品の売上
今回知りたいことは、「広告宣伝費(今回は簡単のためTVの宣伝費に限定します)は本当に商品の売上を上昇させているか?」ということです。
線形回帰分析はある変数(データ)を別の変数(データ)で説明・予測するための適切なモデルを、観測データから構成するデータ解析法の総称でした。
例えば、salesをTVによって説明できるモデルを構成すれば、広告宣伝におけるTVの有効性が検証できます。
早速やってみましょう。
線形単回帰分析
今回は線形回帰分析の中でも最もシンプルな方法:単回帰分析を行います。
まず、salesがTVの1次関数で近似的に説明できると仮定します。
sales ≈ β0 + β1 × TV
salesは目的変数、TV(宣伝費)は説明変数です。
β0 、β1は回帰係数と呼ばれます。
もしβ1が十分に大きければ、テレビにおける宣伝費は有効だということが言えます。
ではβ0 、β1の適切な値はどのように求めれば良いのでしょうか?
今、200の異なる市場におけるsales(売上)とTV宣伝費のデータが手元にあります。
ここでは、i番目の市場におけるTVの値をxi、salesの値をyiと書くことにします。
目標:以下の近似が、全ての i = 1,2,…n =200 について、限りなくよくなるように、β0 とβ1の値を決めたい。
yi ≈ β0 + β1 × xi
つまり、点(x1,y1),(x2,y2),…,(xn,yn)の全てに対して、可能な限り近くなるように、
直線yi ≈ β0 + β1 × xi を引きたいと考えています。
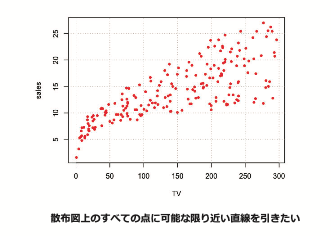
最小二乗法
では yi と β0 + β1 × xi の「近さ」はどのように測れば良いでしょうか?
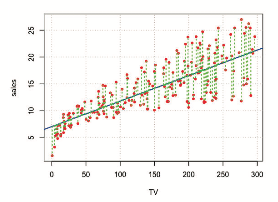
観測値と予測値の距離の近さを測る時、最もよく使われる方法が最小二乗法です。
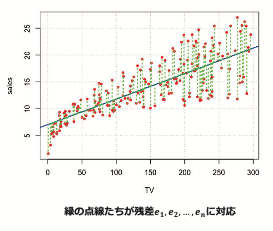
β0 + β1 × xi によって yi を近似した際の残差を ei = yi - ( β0 + β1 × xi ) とした時
全ての残差ができる限り小さくなるには
残差二乗和 E = Σ ei ^2 = e1^2 + e1^2 + … +. en^2 (※1)が最小となれば良いです。
つまり、この残差二乗和Eが最も小さくなるように、β0とβ1を求めることができれば
観測値と予測値が最も近づく直線を描くことができます。
(※1:Σの範囲:i = 1 〜 n まで)
では残差二乗和のEが最小になるβ0とβ1はどうすれば求めることができるのでしょうか?
これは数学の世界で正規方程式と呼ばれる連立方程式(後述)を解くことで、
(残差二乗和Eを最小にする)β0とβ1が求まることが分かっています。
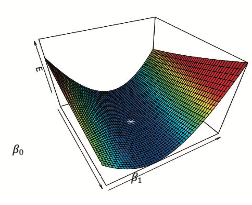
ちなみに上記画像は残差二乗和Eを表す曲面のグラフ E = E ( β0 , β1 )のグラフです。
*が正規方程式の解に対応する点(↔︎曲面が平坦になる点)を表しています。
その正規方程式の解は、次の式で与えられます。
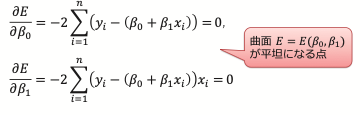
この正規方程式を直接解いて偏回帰係数(実際には観測には必ず誤差が含まれるとされているため、真の回帰係数β0,β1は神のみぞ知る値となり、厳密な値を求めることはできません。そのため、求めたいβ0,β1代わりとして、統計的な知識を使って推定するβ0,β1を、偏回帰係数とよび、これを使って近似線を決定します。この偏回帰係数は、一般的にβ0hat、β1hatと表現されます。)を求めることも可能ですが、
Rを使えば、簡単にβ0hat , β1hatを求めることができます!
下記が実際のRのコードになります。

これを実行した結果は下記になります。

この分析結果から、(β0hat = 7.03259)β1hat = 0.04754 が求まったことから
手元にあるデータについては「テレビの宣伝広告費は売上を上昇させる」ことが分かりました。
しかしここで気をつけたいのは、あくまで手元のデータにおいて、上記の関係が言えるということです。
本当に知りたいのは上の関係が一般的に成立するか否か(新たな市場で商品を売る際に、テレビでの宣伝が売上に繋がるか?)ということです。
これを考えるには、推測統計の枠組み(ランダムネスの導入と活用)を利用する必要があります。
推測統計の枠組み(ランダムネスの導入と活用)を利用するとは、
標準誤差(β1hatの標準偏差)を求めて、β1hatの有意性(求めた偏回帰係数β1hatは統計的に正しいと言っていいか)を検定することを指します。
具体的な手順としては、推定精度の評価→標準誤差の推定→有意性の検定とステップを踏んで行いますが
こちらもRを使えば簡単にβ1hatの「大きさ」「有意性」(すなわち一般的にテレビの宣伝広告費は売上を上昇させると言えるか)を確認することができます。
下記がその実際のコードです。

この結果は下記になります。

以上より、β1hatは有意であることが分かりました。
いかがでしたでしょうか?
統計的な知識やRのプログラミングの話もあり、難しいと感じた人も少なくないのではないでしょうか。
それでは今度はExploratory を用いて、単回帰分析を行ってみたいと思います。
Exploratoryでは手元のデータについての関係だけでなく、上記の推測統計の枠組みも自動で行い、
「一般的にTV広告費はsalesに影響を与えているか、どんな影響を与えているのか(新たな市場でも商品を売る際に、テレビでの宣伝が売上に繋がるか?)」
確認することができます。
Exploratoryのアナリティクス単回帰分析を紹介
早速Exploratoryを用いて単回帰分析を実行してみましょう。
用いるデータ
単回帰分析には、1行が1観測対象となっているデータが必要です。
分析に用いるサンプルデータとして、今回も同じく売上とメディア別広告費を使用します。このデータは、1行がある商品の1つの市場における広告費の内訳を表しています。
このサンプルデータは全部で200行あるので、200の異なる市場におけるある商品の売上と広告費をまとめたデータということになります。
単回帰分析を実行する
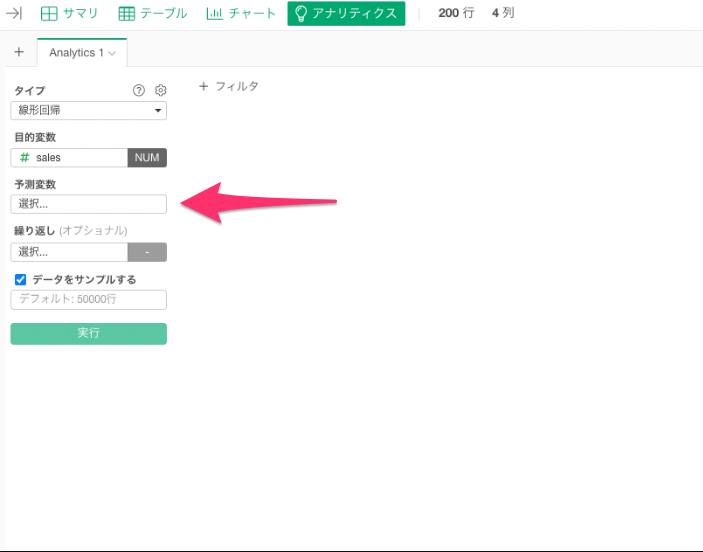
アナリティクスビューを開き、タイプに「線形回帰分析」を選択します。
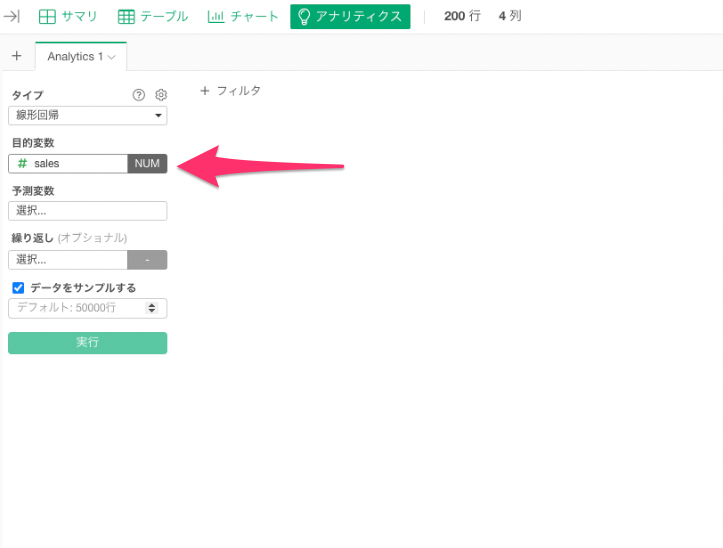
目的変数の列をクリックして、予測したい変数を選択します。
今回は売上金額を予測したいので、目的変数に「sales」を選択します。
次に予測(説明)変数の列をクリックして、予測に使用する列を選択し、右下にあるOKを選択します。
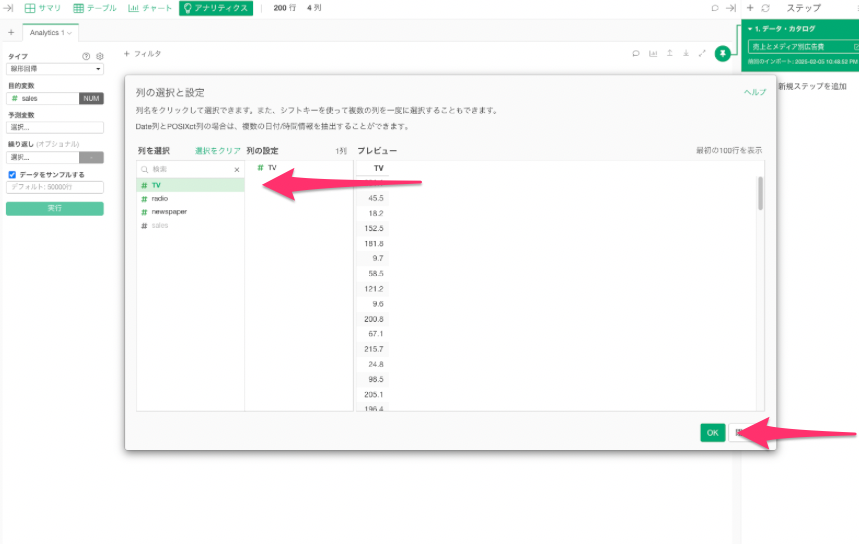 ちなみにシフトキーを押すことで複数の列(「radio」や「newspaper」)を一気に選択することもでき、そのまま重回帰分析も行うことができます。
ちなみにシフトキーを押すことで複数の列(「radio」や「newspaper」)を一気に選択することもでき、そのまま重回帰分析も行うことができます。
列の指定が完了したら、左側の緑の「実行」を選択することで、線形回帰分析の結果が表示されます。
表示される実行結果
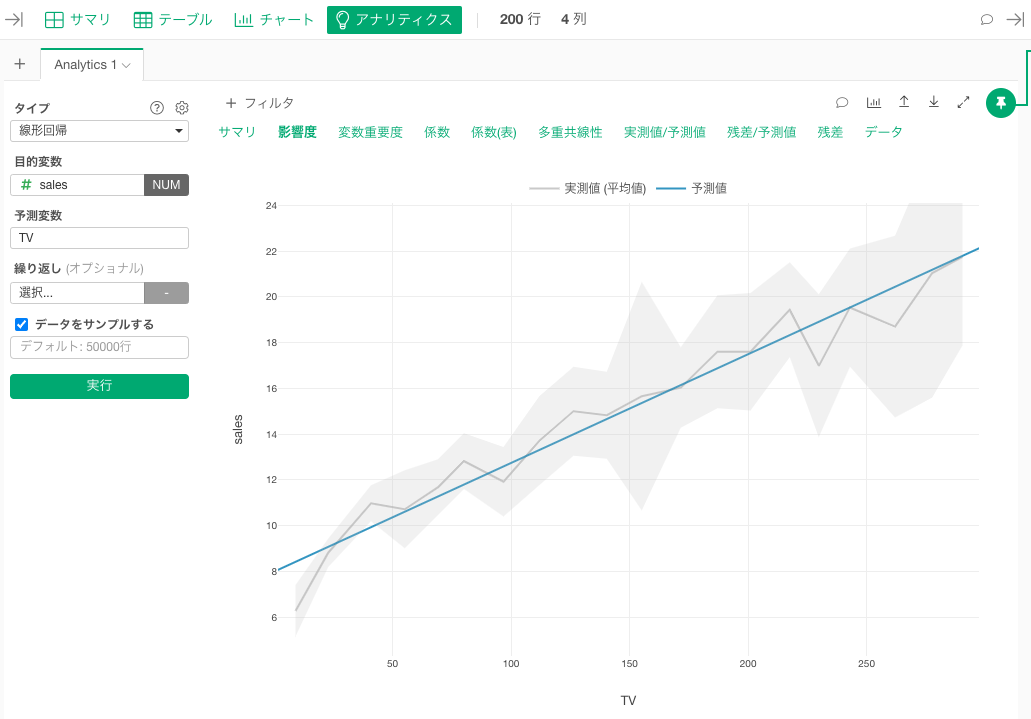
結果の解釈
影響度
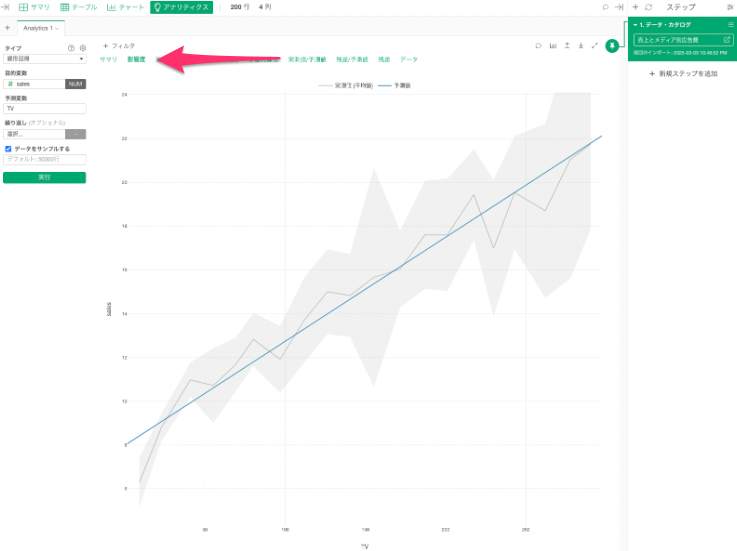
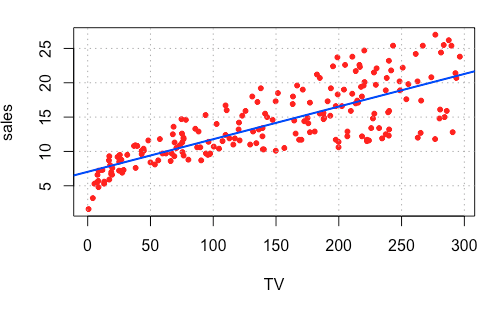
影響度のタブでは、予測(説明)変数と目的変数の関係を視覚的に確認することができます。
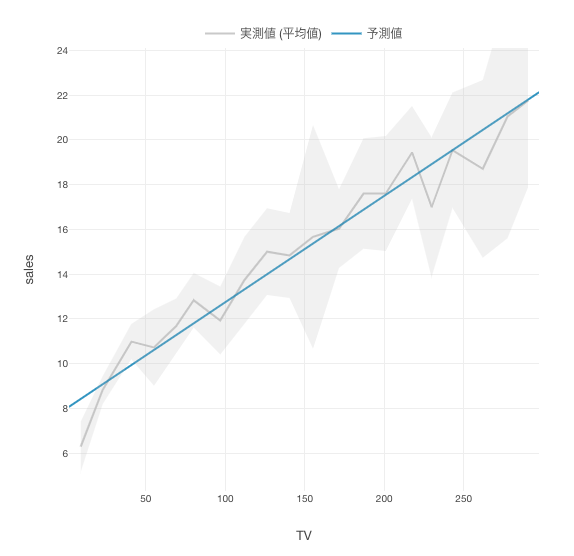
上記のグラフを見ると、この商品においては、テレビ広告費をかければかけるほど、売上金額が上昇していくことが視覚的に確認することができました。
サマリ
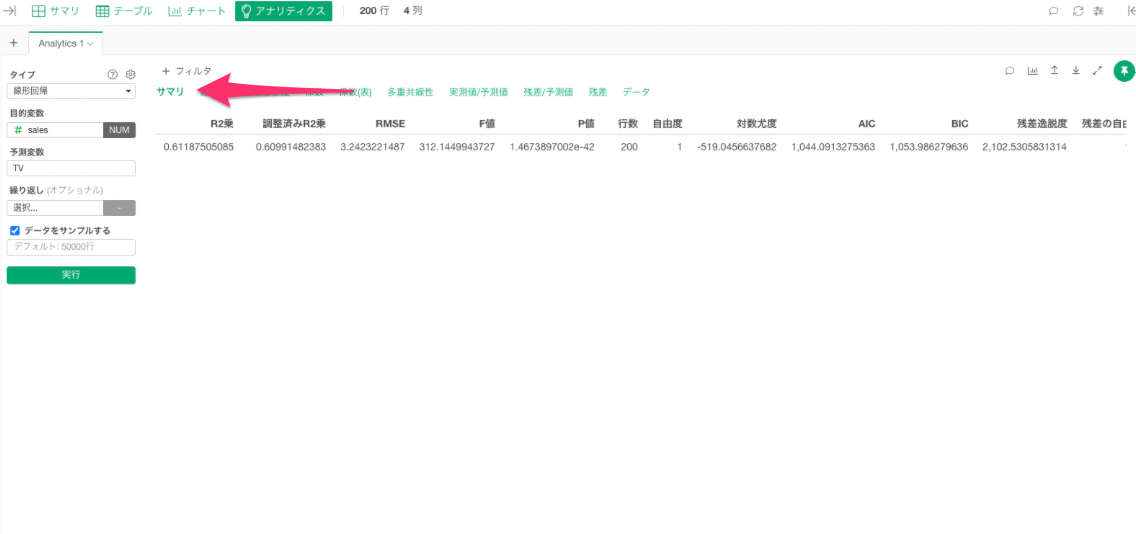
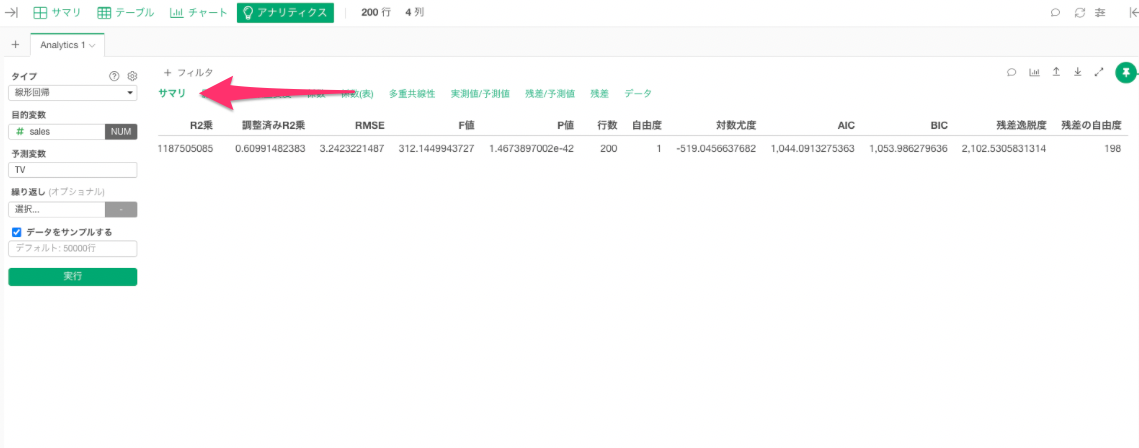
サマリタブでは様々な評価指標における結果の詳細を確認することができます。
係数(表)
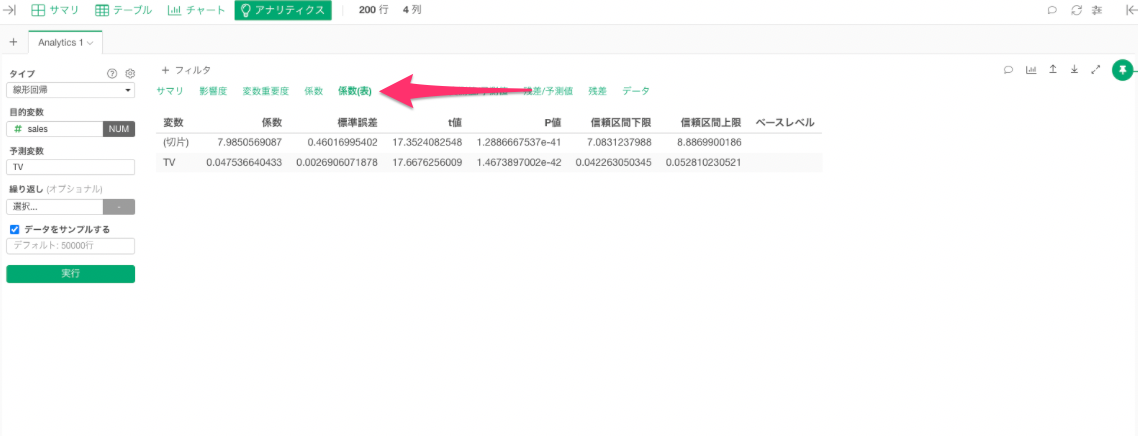
係数(表)タブでは、 y = β0hat + β1hat * x における
β0hat 、 β1hat(偏回帰係数)をはじめとした、統計量の具体的な数値を確認することができます。
実際にTVの偏回帰係数を見てみましょう。
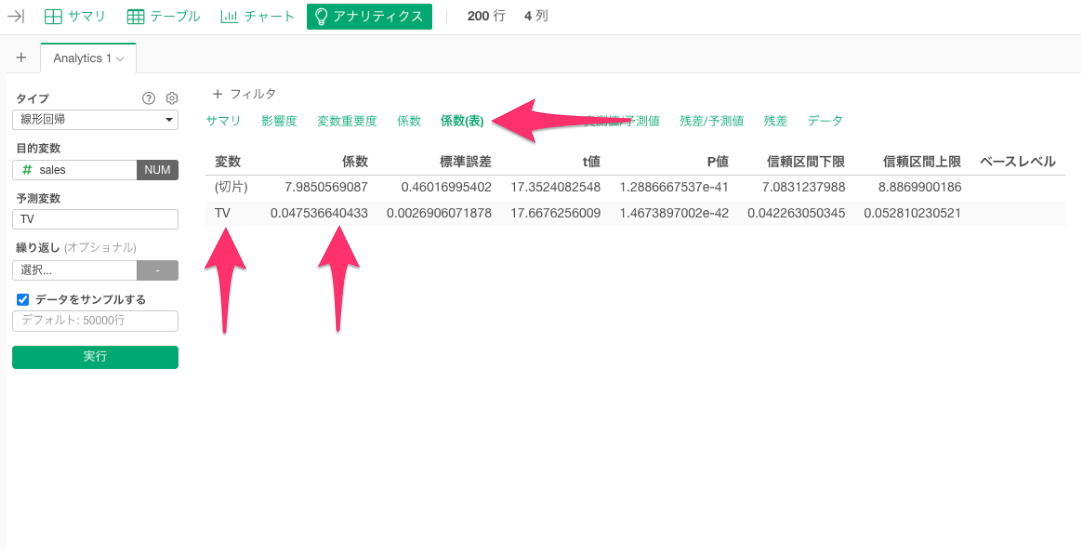
TVの偏回帰係数は「0.047536640433」となっています。これはTVの広告費を1単位(今回は千ドルでした)増やすと、salesがは0.047536640433(単位:千ドル)増えることを意味しています。
この値は統計的に意味がある数値と言ってよいか(有意と言えるか)、P値を確認してみます。
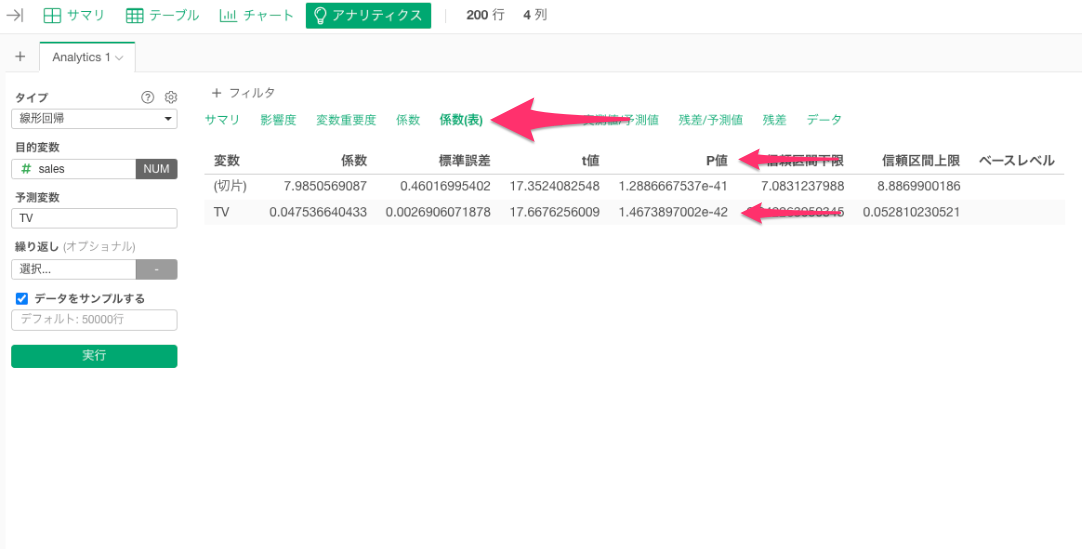
P値を見ると、「1.4673897002e-42」となっています。
e-42はネイピア数e(約2.718)を-42乗した値です。具体的な値を計算すると
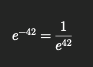
となり、「0.0000000000000000005749 」という極めて小さな数値になります。
P値は帰無仮説が正しいと仮定した時に、観測されたデータ以上に極端な結果が得られる確率を示しました。
つまり今回のケースでは、帰無仮説「TVの広告費はsalesの上昇に影響しない」が正しいと仮定した時、たまたまこういうデータ(ある商品の異なる200の市場におけるTVとsalesの観測データ)が出る確率は、「0.00000000000000005749%」だということになります。
この確率をどのように解釈すればよいでしょうか?
統計の世界では、これだけ稀にしか起きないことが「今回はたまたま起きた」と判断するのではなく、前提に置いた仮説が間違っていたと判断し、帰無仮説を棄却
つまり**「TVの広告費はsalesの上昇に影響する」**ということが分かりました。
(ちなみにデータ分析を実務で行う場面では、一般的に分析を行う前に有意水準を定め、その有意水準と分析結果のP値を比較し、有意かどうかを判断しています。)
P値を基にした有意性の検定とは別の観点からも、TVの偏回帰係数は有意なのか(=TV広告費はsalesの上昇に影響があるのか)見てみましょう。
これは信頼区間を確認することで判断することができました。
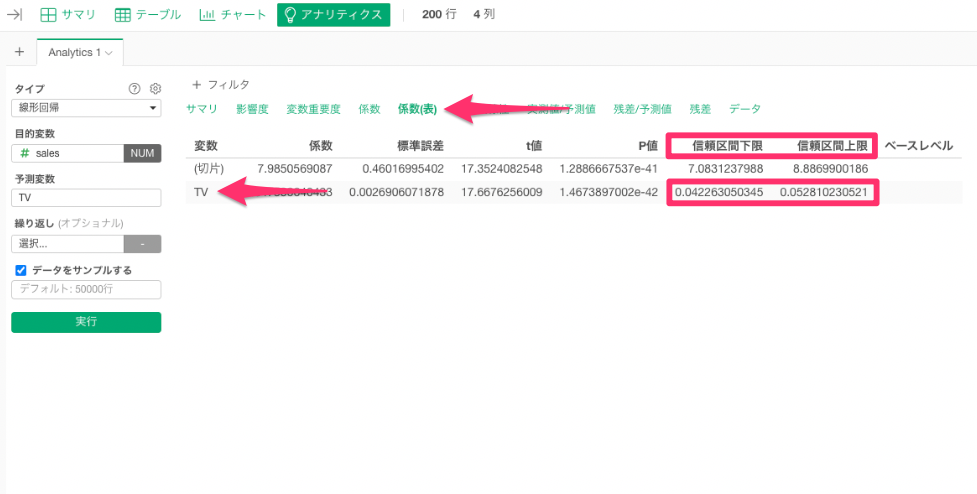
信頼区間は、母集団の真の値(推定値の偏回帰係数ではなく、神のみぞ知る値である回帰係数)が含まれていると考えられる範囲のことを指しました。
今、TVの信頼区間は、下限が0.042263050345、上限が0.052810230521となっています。
つまり真の値(TVの回帰係数)は95%(デフォルトで95%で設定して計算しているため)の確率で、
「0.042263050345」から「0.052810230521」の値の範囲にあることが分かります。
この結果をどのように解釈すればよいでしょうか?
もし仮に、TVの回帰係数が「0」だった場合、TV広告費をいくらかけても係数で0をかけることになるので、TVの広告費にお金をかけることは意味がないことになってしまいます。
しかし今、TVの回帰係数は95%の確率で
0.042263050345 ≦ TVの回帰係数 ≦ 0.052810230521 の範囲にあることが分かっているため
やはり**「TVの広告費はsalesの上昇に影響する」**ということが分かりました。
一般的に信頼区間で有意性を確認する際は、信頼区間の下限と上限が「0」をまたいでいなければ、有意だと判断することができます。
これを視覚的に一瞬で確認することができるのが、係数タブになります。
係数
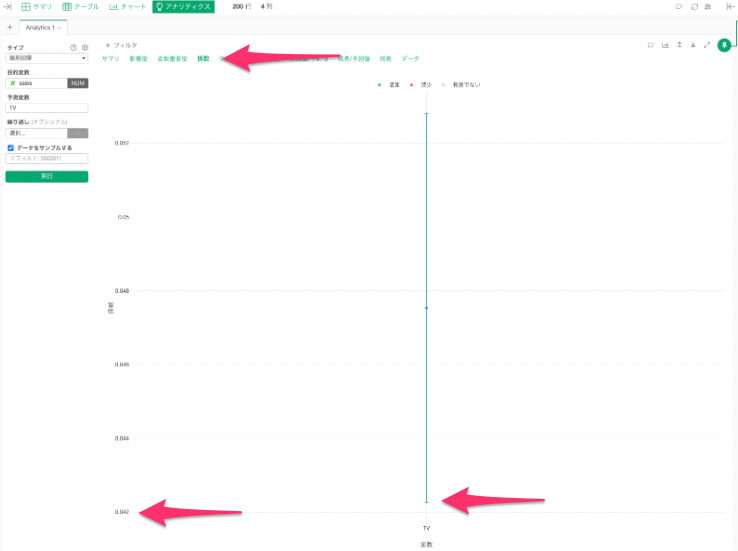
係数タブでは、信頼区間の範囲、0をまたいでいないか、グラフで確認することができます。
また色を使って有意かどうか、増加の影響を与えているか/減少の影響を与えているのか、一目で確認することができます。
有意でなければ、真ん中の線はグレーになります。
有意で減少の影響があれば、線は赤色になります。
今回は有意で増加の影響を与えているので、線は青になっています。
信頼区間の範囲を見ても、下限の値が0を超えており、0をまたいでいないことが確認できました。
実測値/予測値
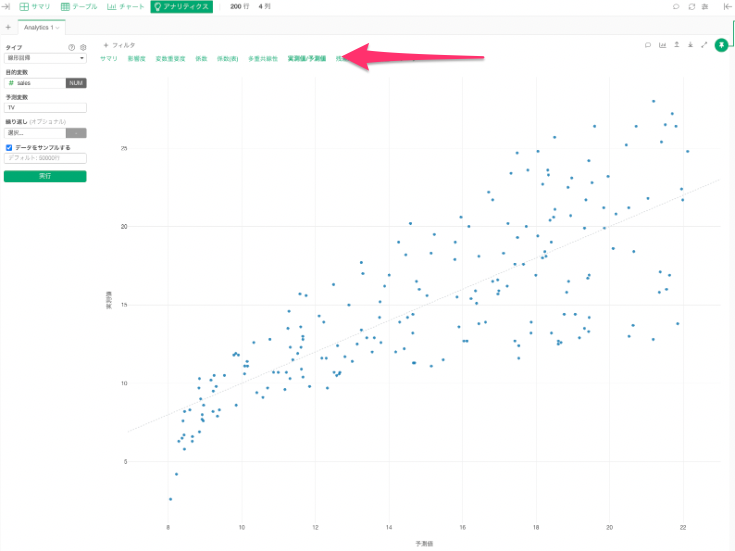
実測値/予測値タブでは、実際の観測値と予測値(全ての観測値にできる限り近くなるように引いた直線上の値)を俯瞰して、視覚的に確認することができます。
残差/予測値
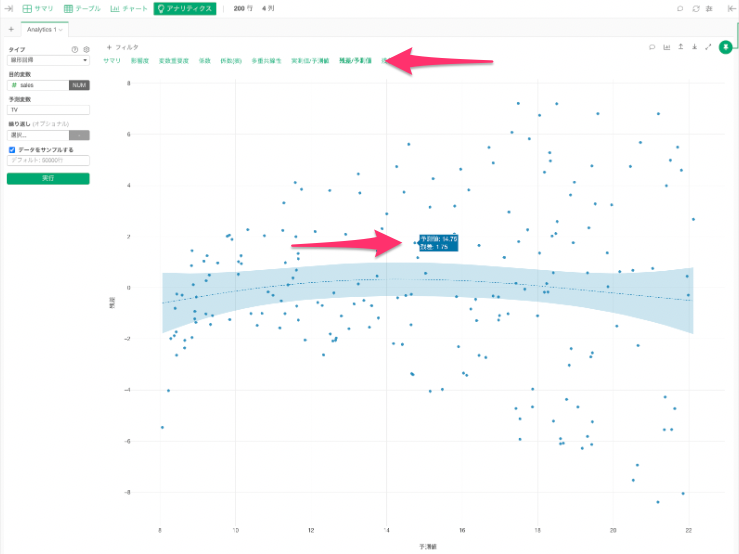
残差/予測値タブでは、残差と予測値の関係性を視覚的に確認することができます。
またマウスのポインタをプロットされている点に合わせることで。予測値と残差の値を具体的に確認することもできます。
残差
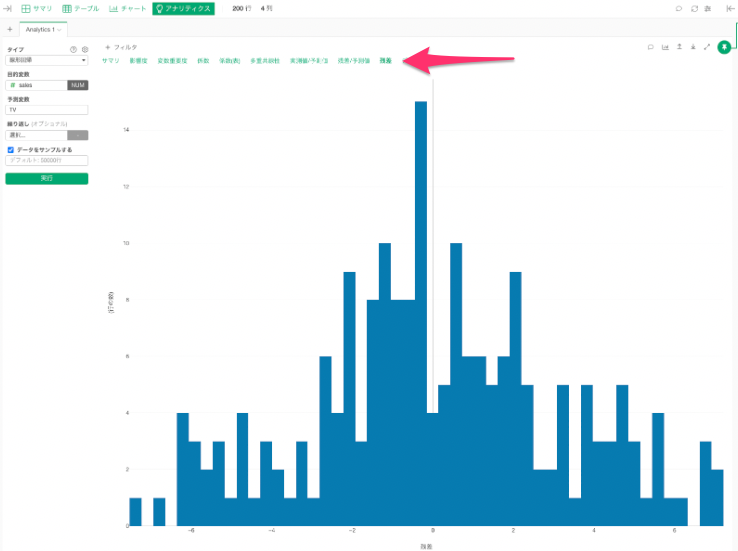
残差タブでは、残差のばらつきをヒストグラムで視覚的に確認することができます。
残差が0の付近に集中していることが確認できました。
データ
データタブでは、200の市場における観測値や予測値、各種統計量も具体的な数値を一覧で確認することもできます。
このようにExploratory デスクトップのシンプルでモダンなUIは、データの加工、可視化、 統計や機械学習のアルゴリズム、ダッシュボードやレポートの作成といったデータサイエンスには欠かせないタスクを簡単に行うことを可能にします。
今回は線形回帰分析とは何なのか、実際にデータを用いながら線形回帰分析の一つである単回帰分析について詳しく解説しました。
ぜひ実際に線形回帰分析を使って業務の改善に活用してみてください。