統計の予測モデルにおける単回帰と重回帰の違い
単回帰と重回帰は、どちらも予測を行うための統計手法ですが、使用する説明変数の数が異なります。
単回帰:1つの説明変数から目的変数を予測する手法
重回帰:複数の説明変数から目的変数を予測する手法
例えば、給料を予測する場合を考えてみましょう。単回帰では「勤続年数」から給料を予測しますが、重回帰では「勤続年数と職位の両方」から給料を予測します。
単回帰と重回帰の基本的な考え方
なぜ重回帰が必要なのか?
実際のデータでは、複数の要因が結果に影響を与えることがほとんどです。アイスクリームの売上を例に考えてみましょう。
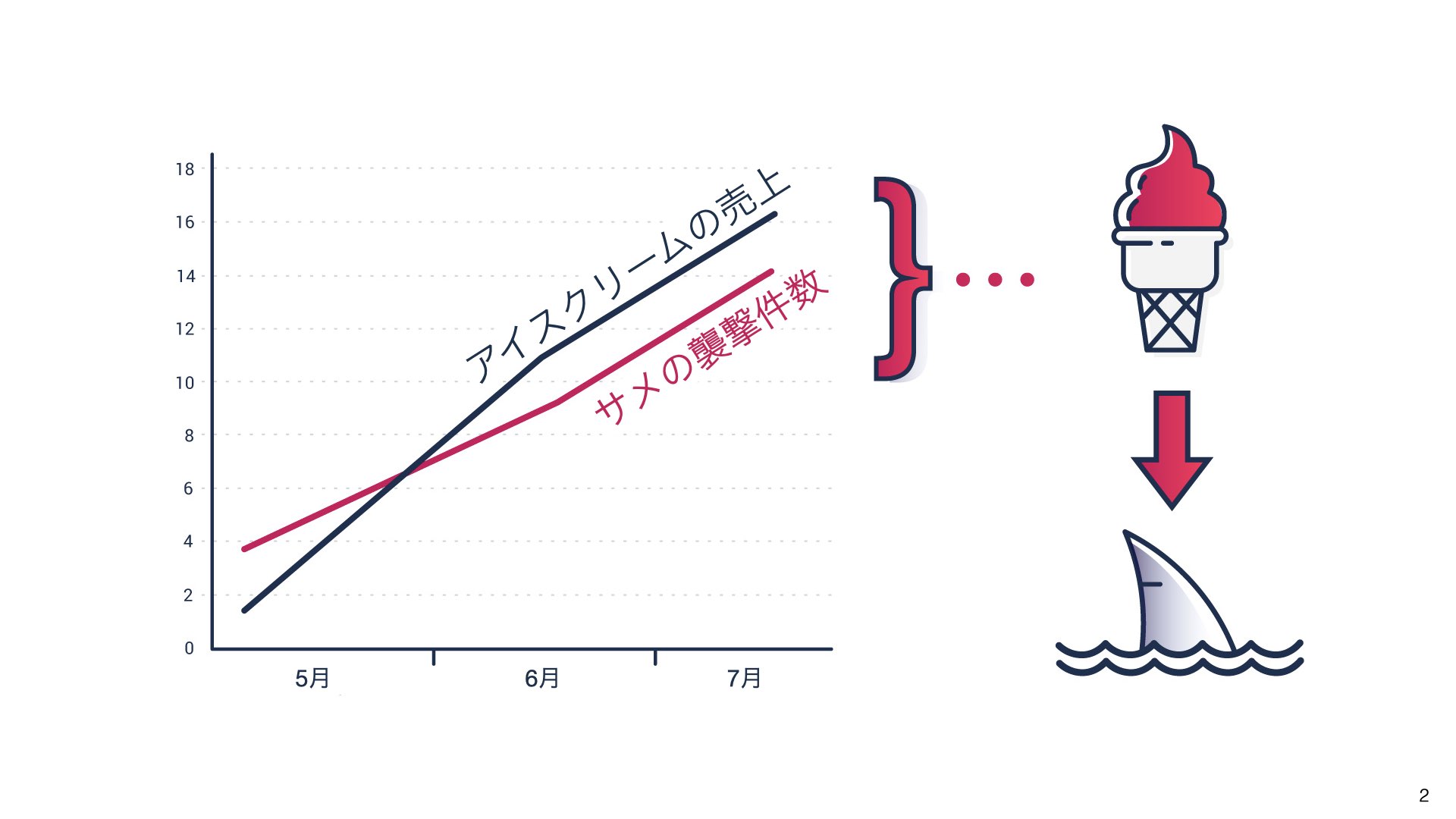
最初は「サメの襲撃回数」と「アイスクリームの売上」に関係があるように見えます。
しかし、実際には「気温」という第三の要因が両方に影響を与えています。
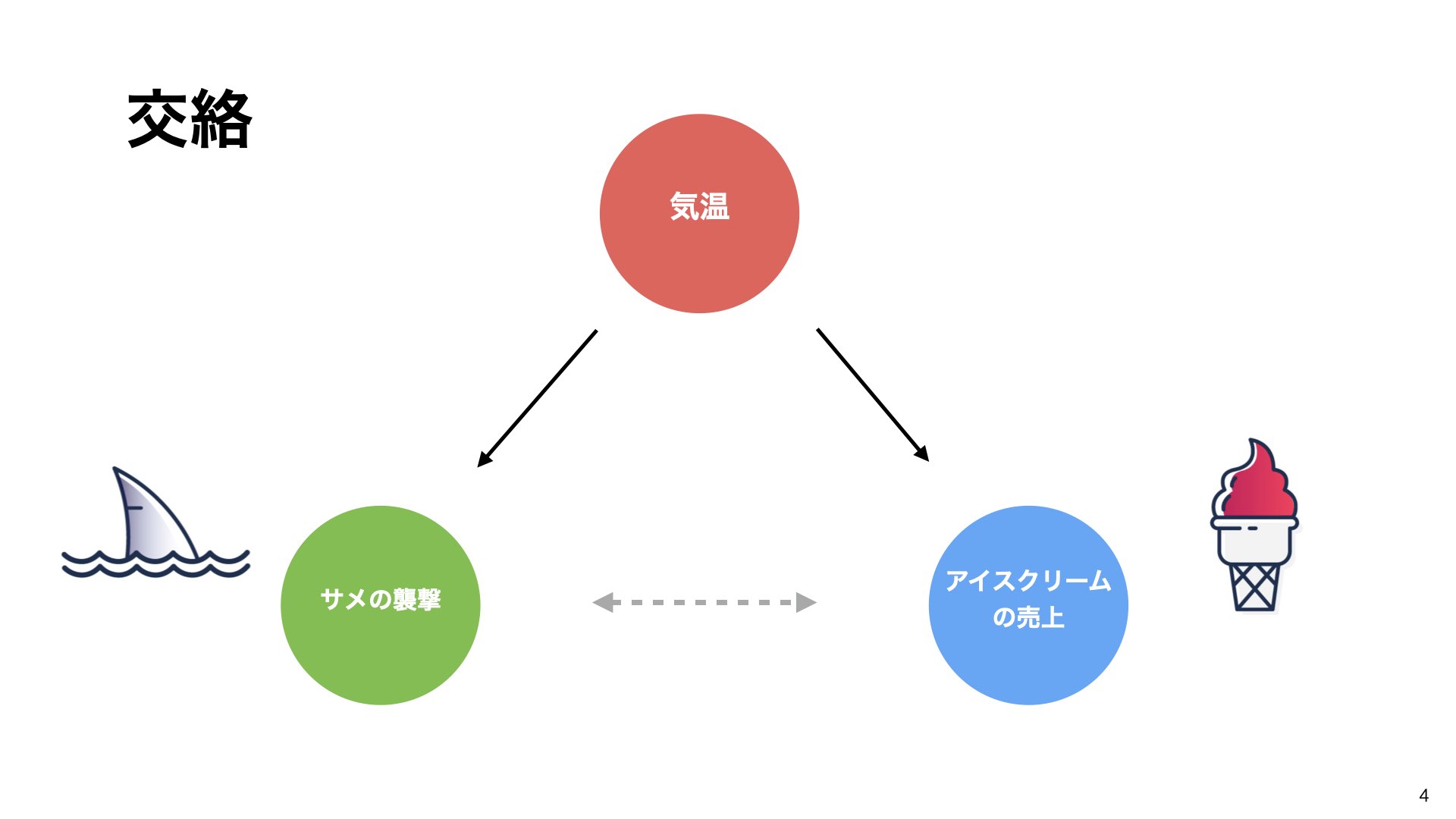
気温が上がると:
サメによる襲撃回数が増える(海水浴客が増えるため)
アイスクリームの売上が増える(暑いため)
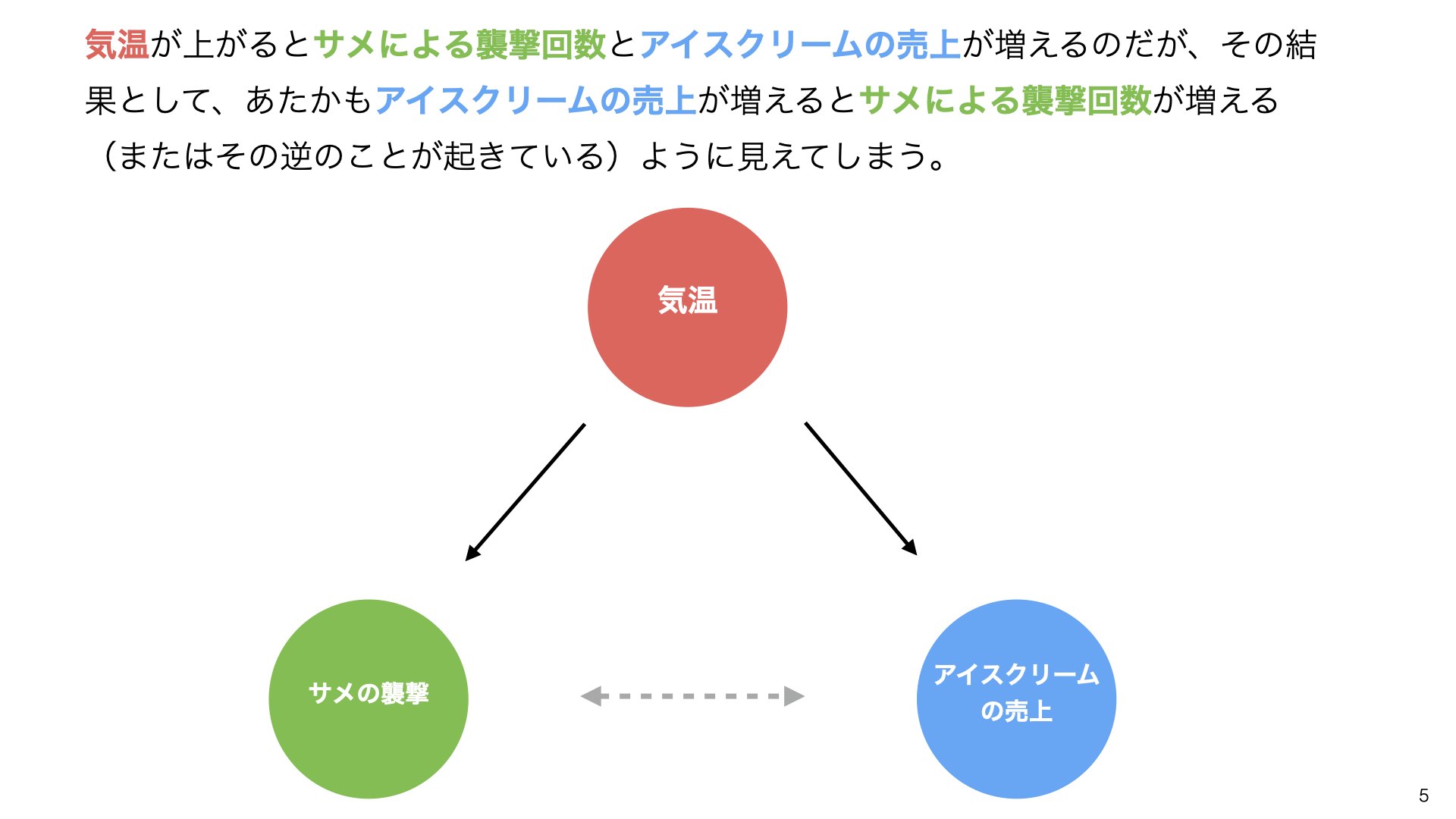
このように、複数の変数が相互に関係している場合、一つの変数が変化すると、もう一つの変数もつられて変化することがあります。
給料予測の例で考える
職位と給料の関係を見てみましょう。
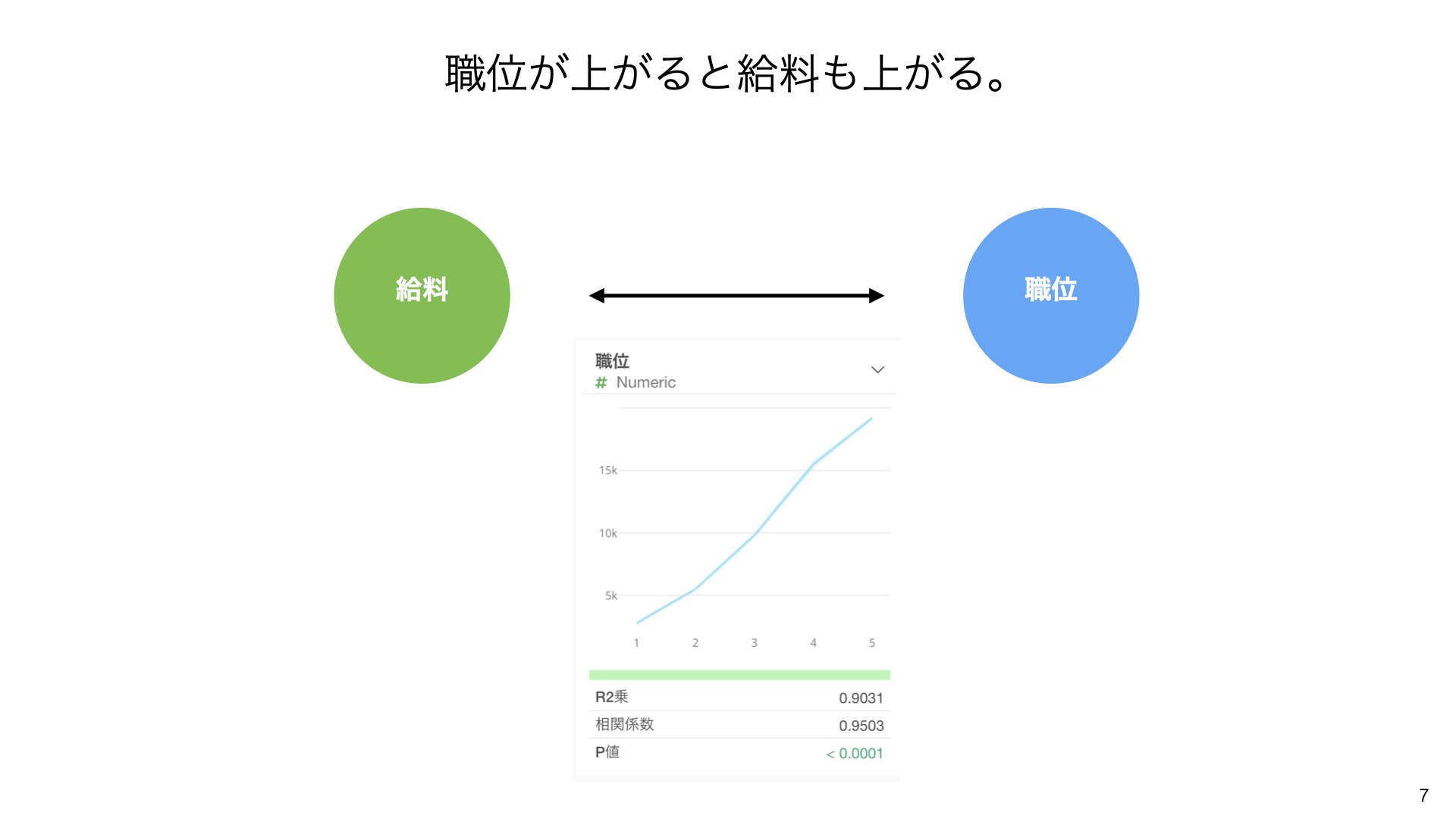
職位が上がると給料も上がる関係があります(R²乗 = 0.9031、相関係数 = 0.9503)。
勤続年数と給料の関係も見てみましょう。
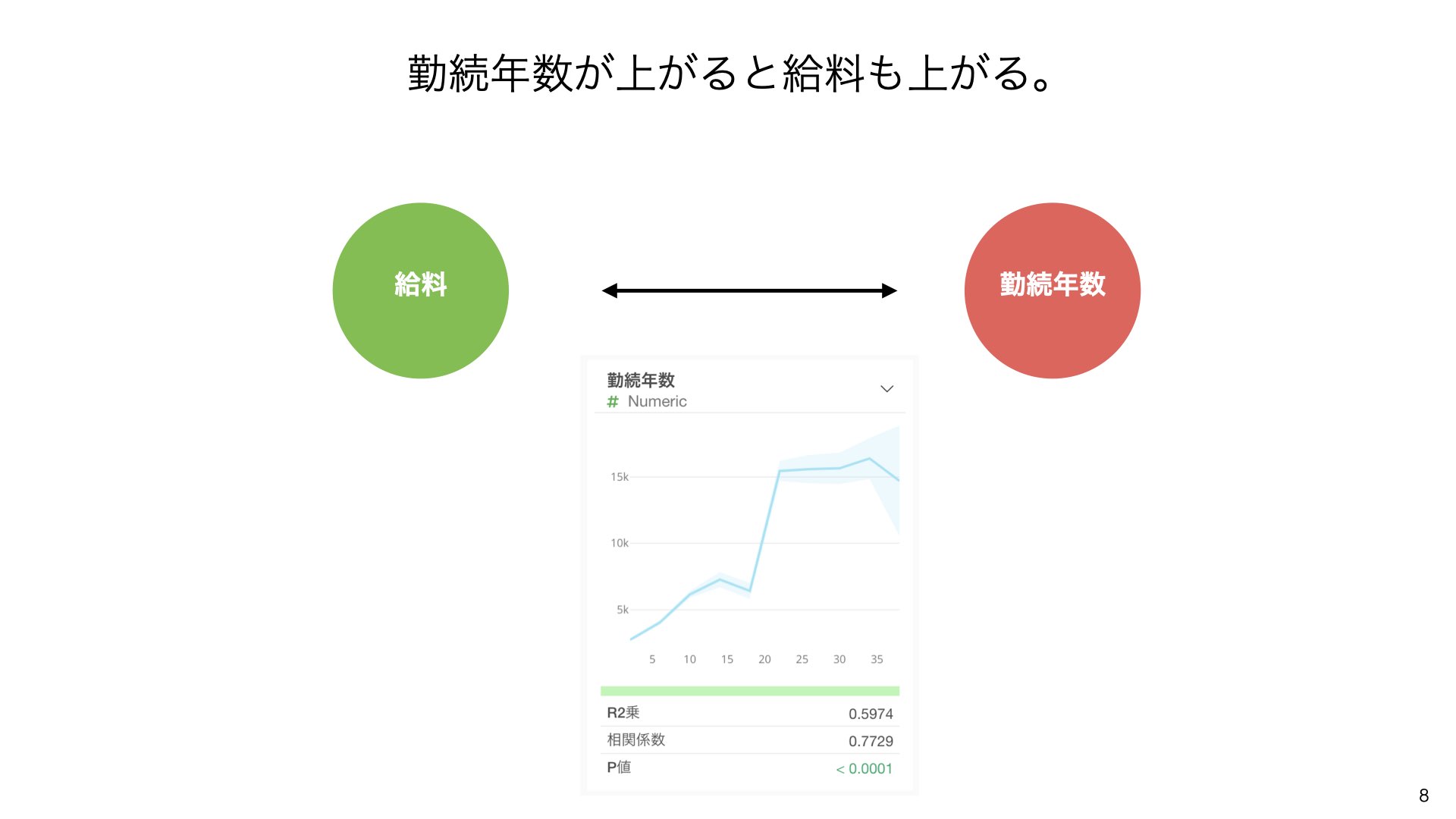
勤続年数が上がると給料も上がる関係があります(R²乗 = 0.5974、相関係数 = 0.7729)。
職位と勤続年数の両方とも給料と相関関係があることがわかりました。
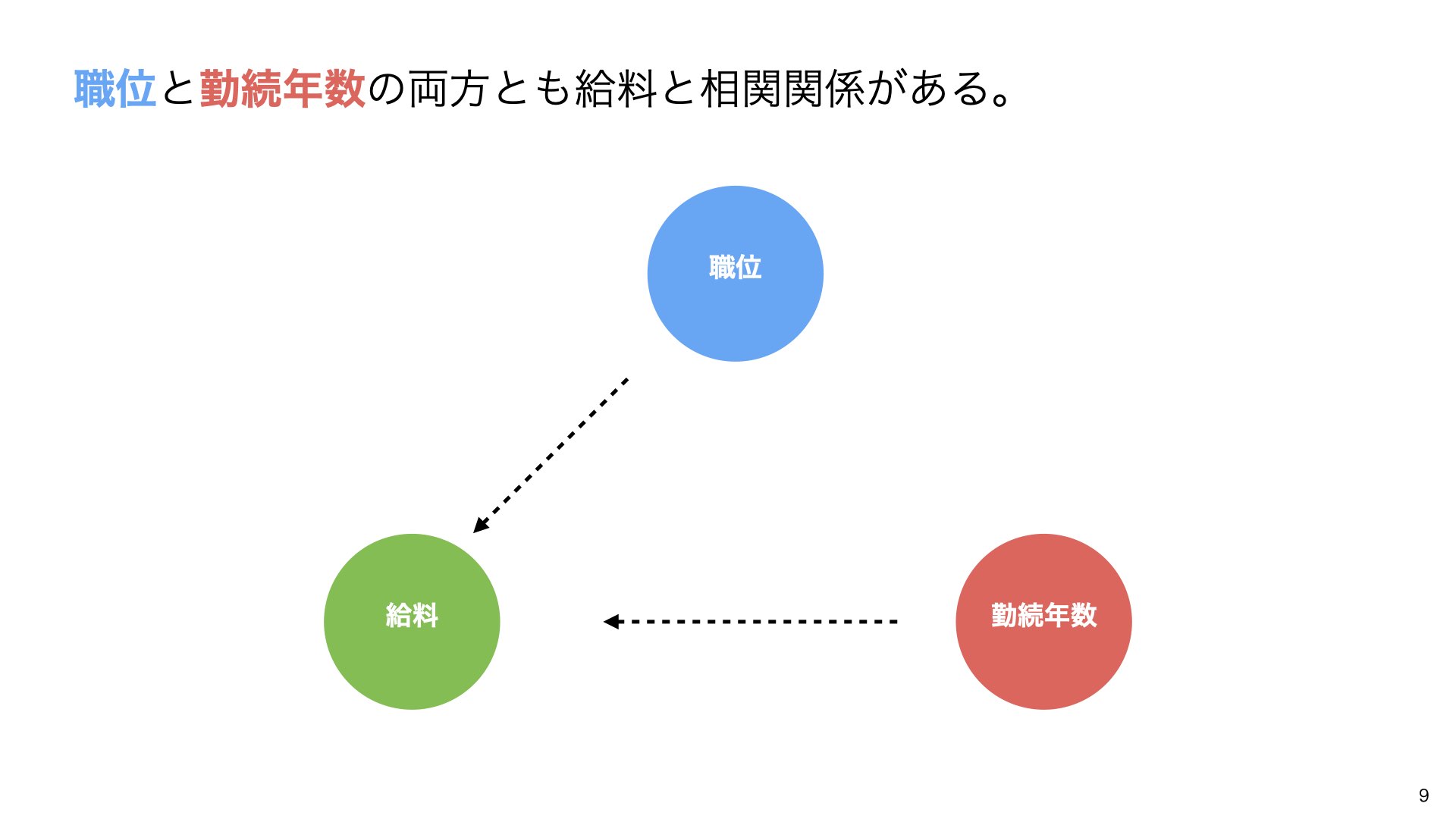
しかし、ここで重要な疑問が生まれます:職位と勤続年数の間には何らかの関係があるのでしょうか?
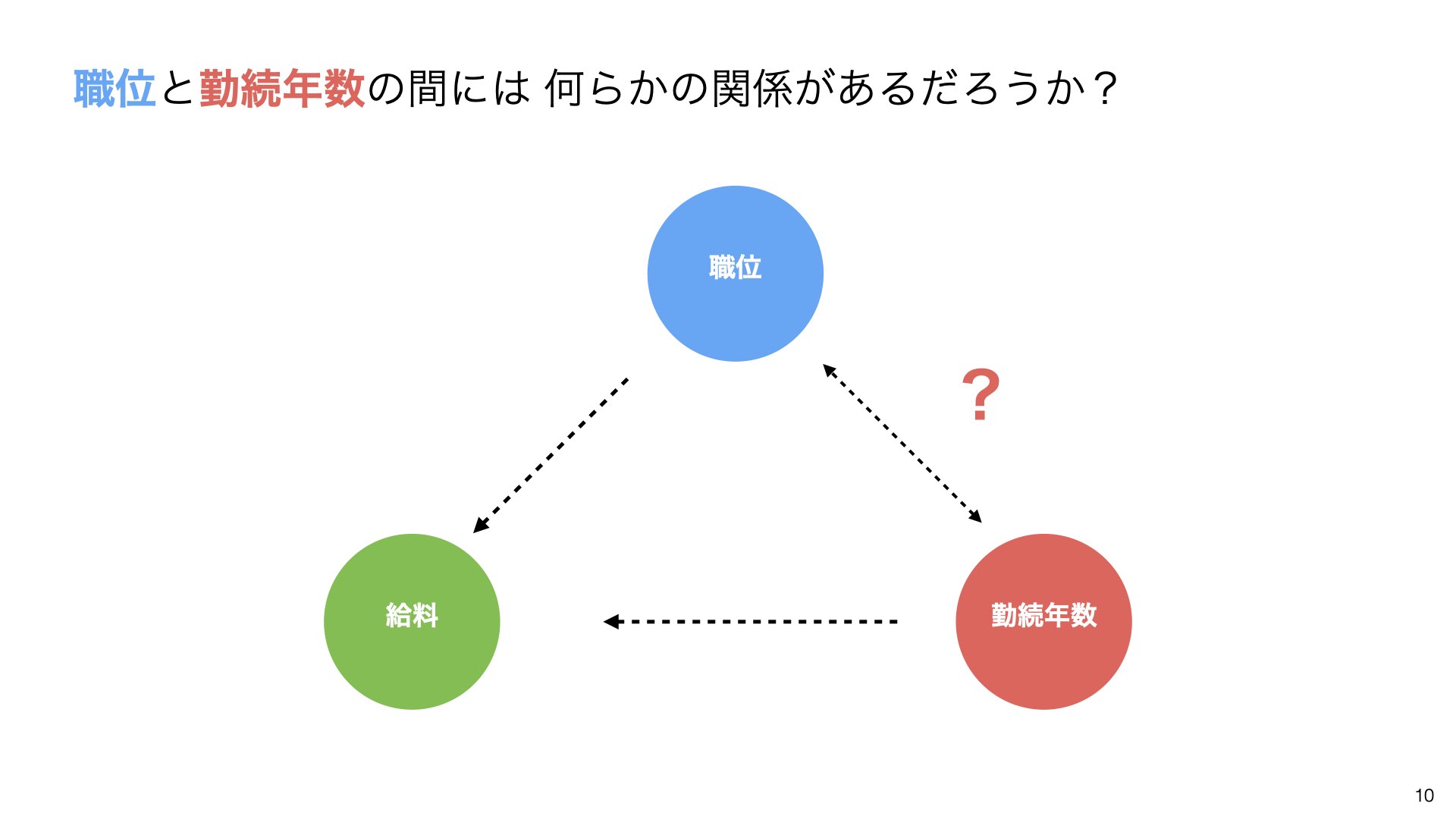
調べてみると、職位と勤続年数の間にも相関関係があることがわかります。
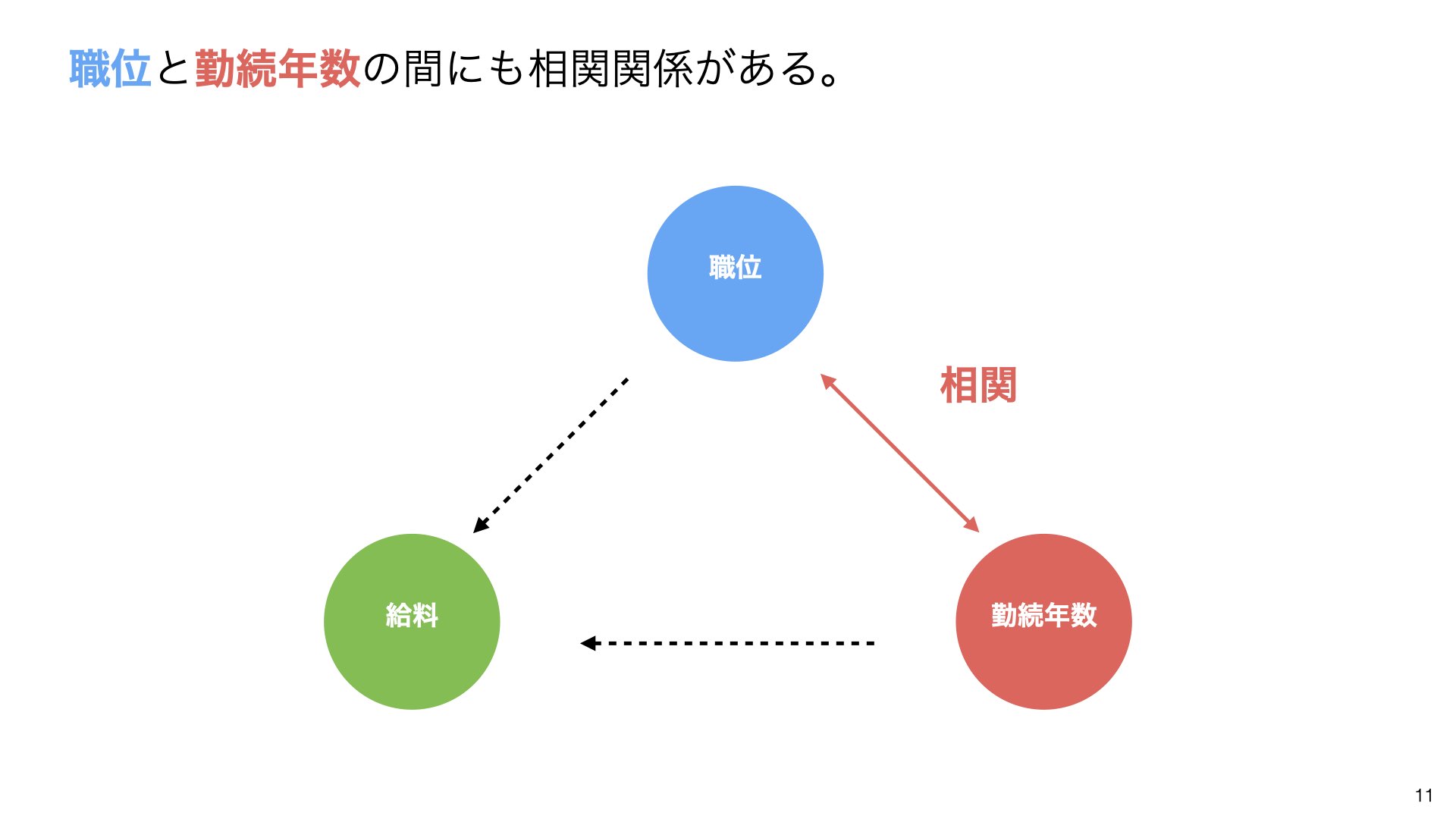
これは理にかなっています:
勤続年数が変わると職位も変わる
勤続年数が変わると給料も変わる
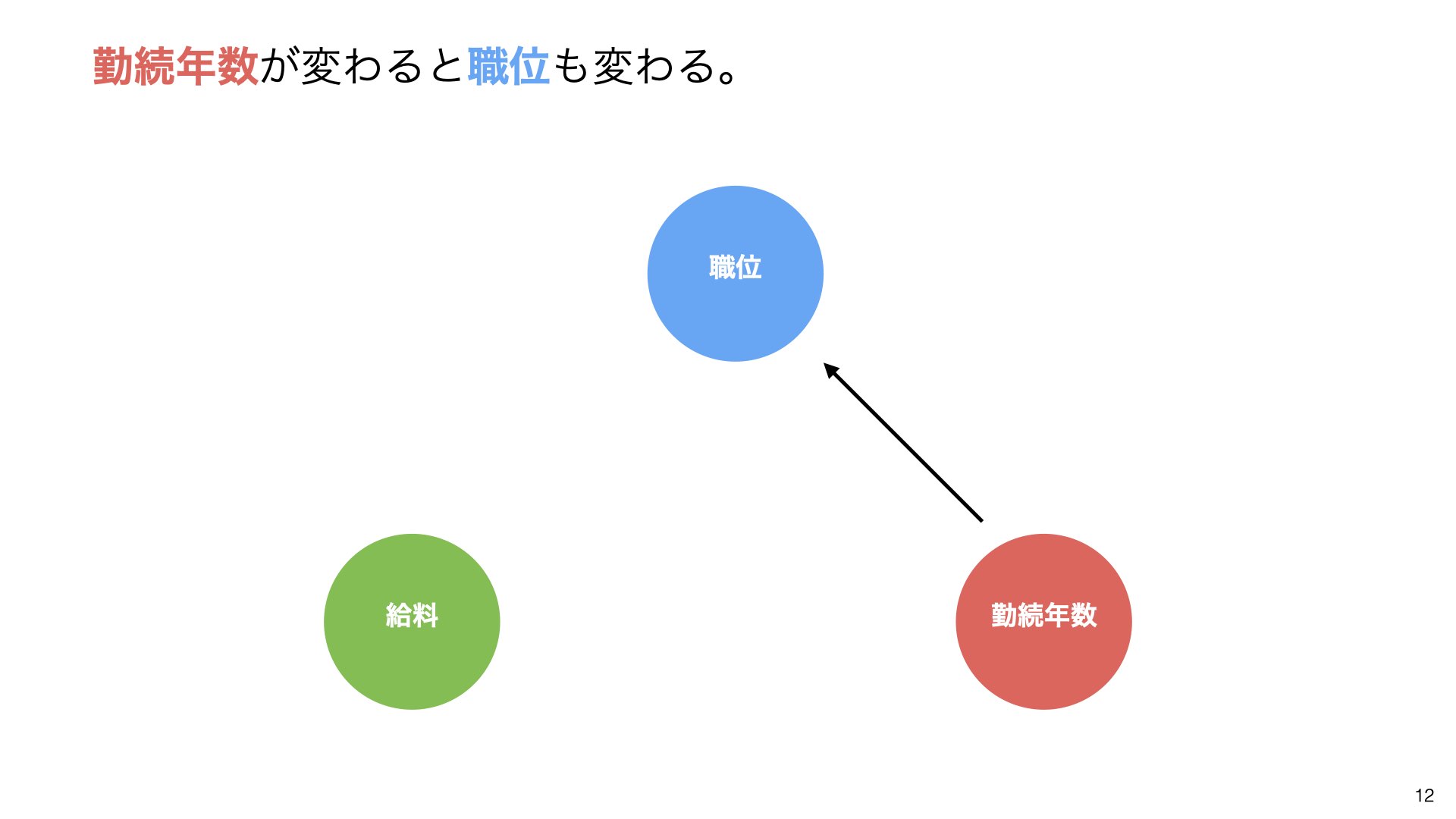
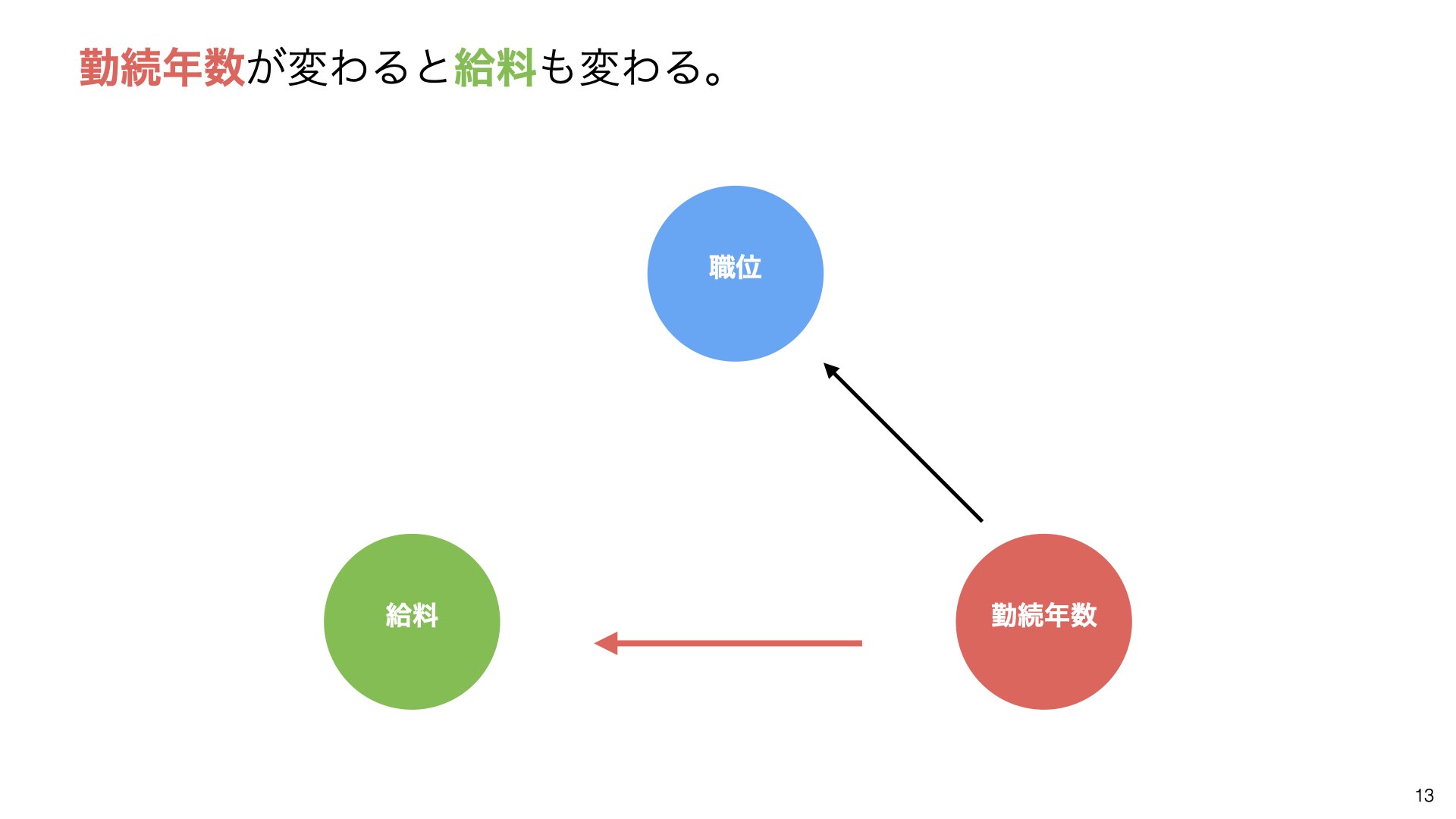
ここで重要な問題が発生します。
勤続年数が変わることで給料も職位も変わるのだが、その結果として、あたかも職位が変わると給料が変わっているように見えているだけではないか?
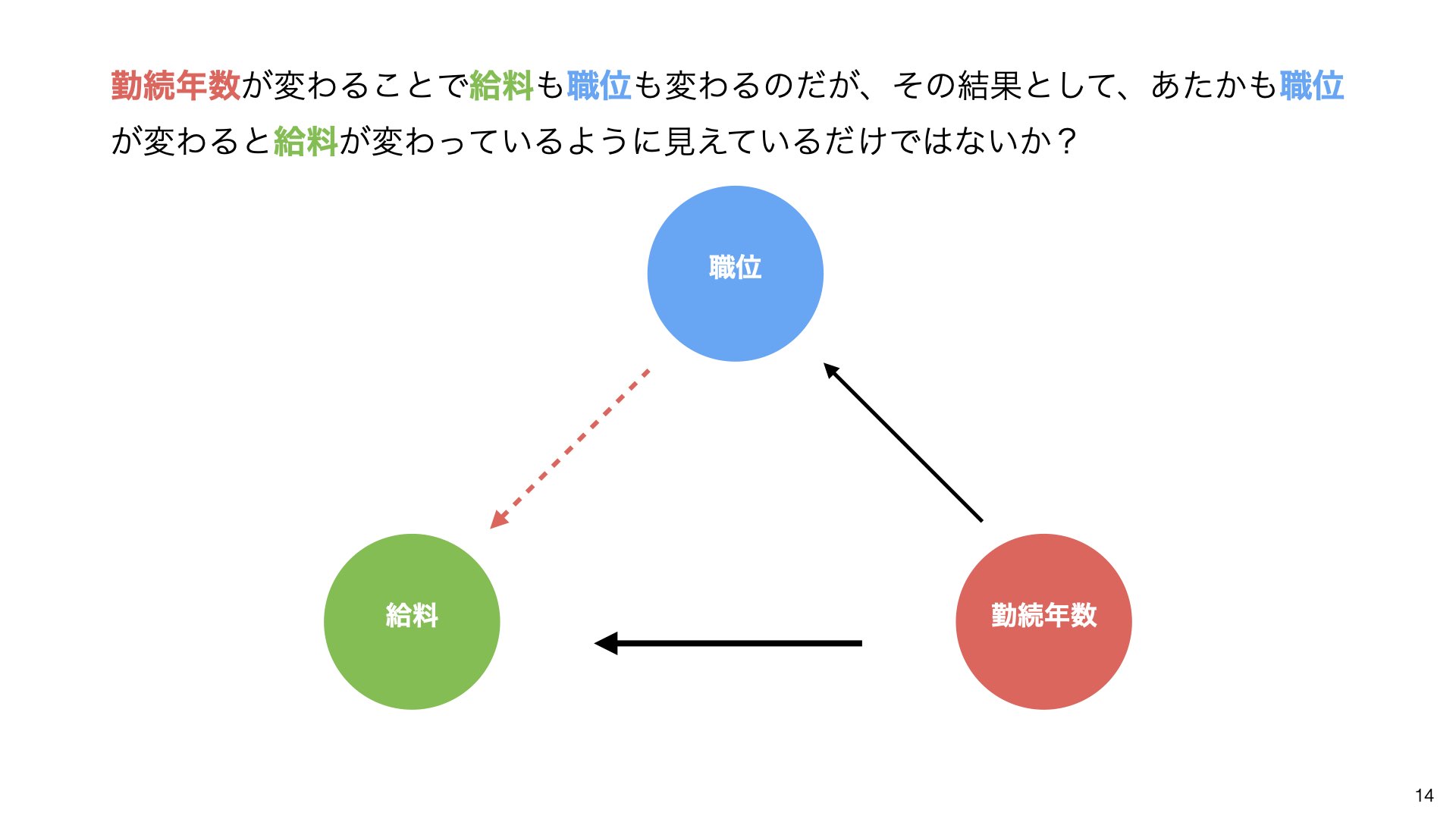
この逆のストーリーも考えられます:職位が高い人は勤続年数も長い
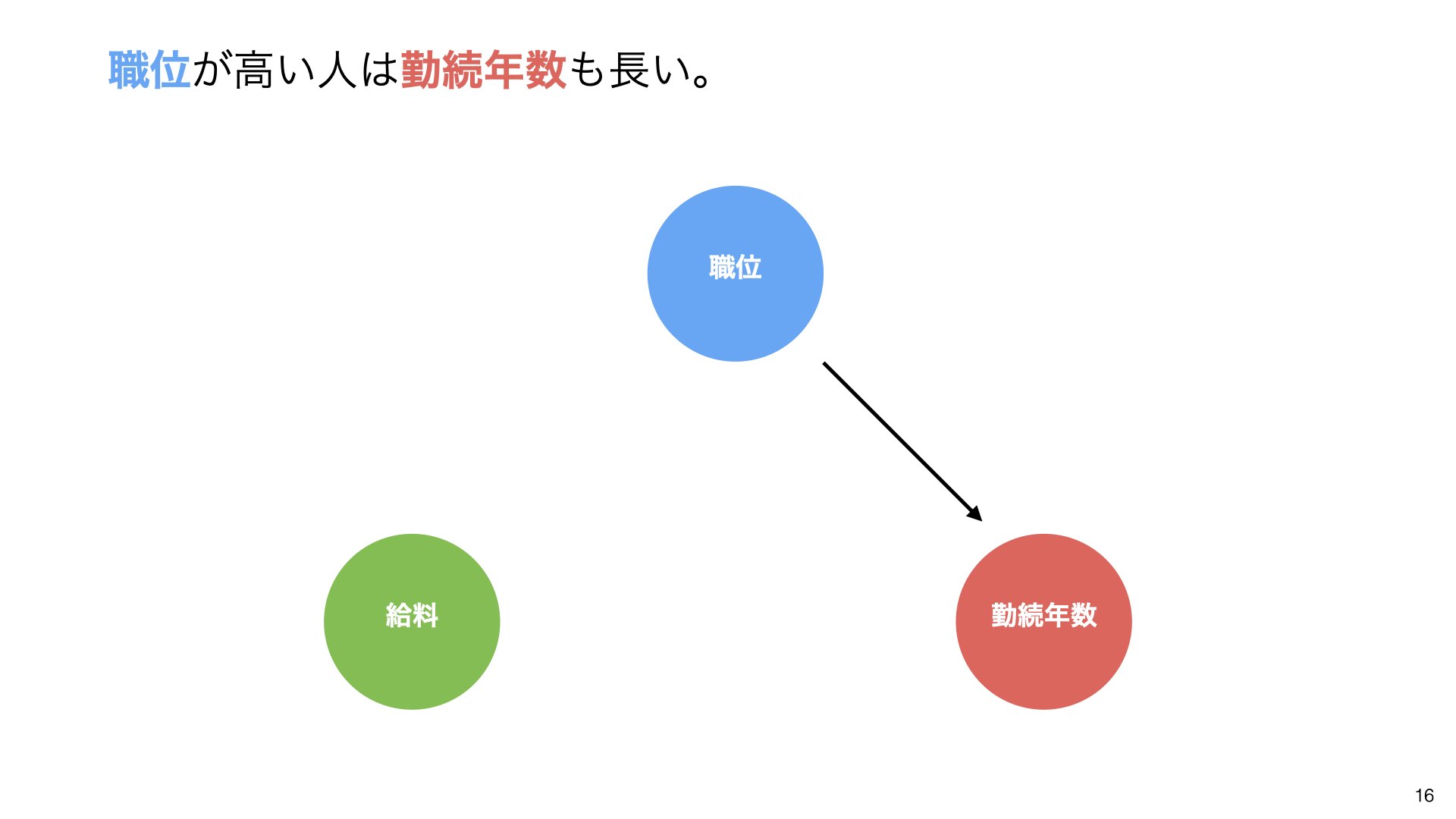
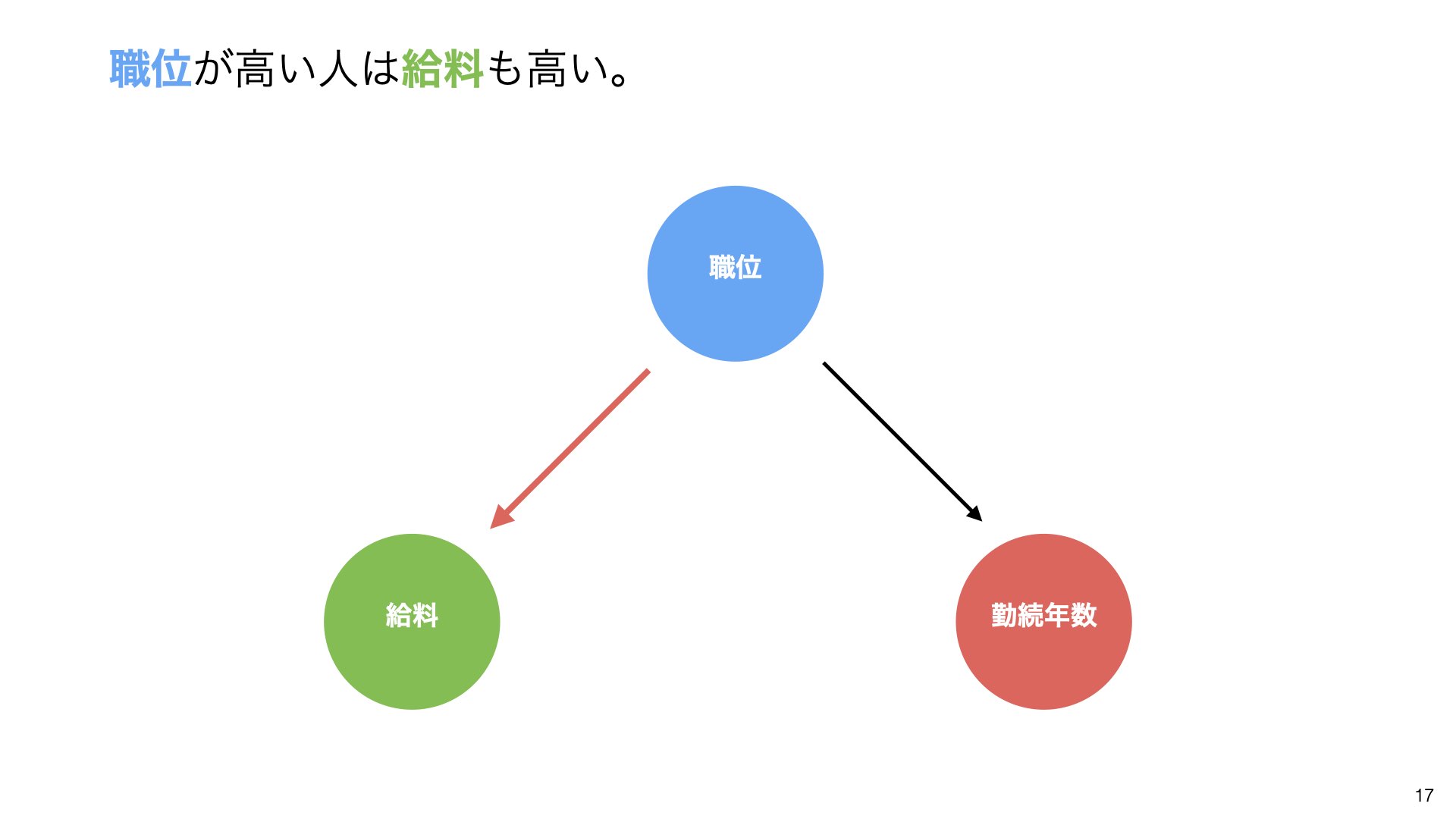
職位と給料、さらに職位と勤続年数の間に直接関係があるだけなのだが、その結果である勤続年数と給料だけ見ていると、あたかも長い期間仕事すれば給料が上がる関係があると見えてしまっているのでは?
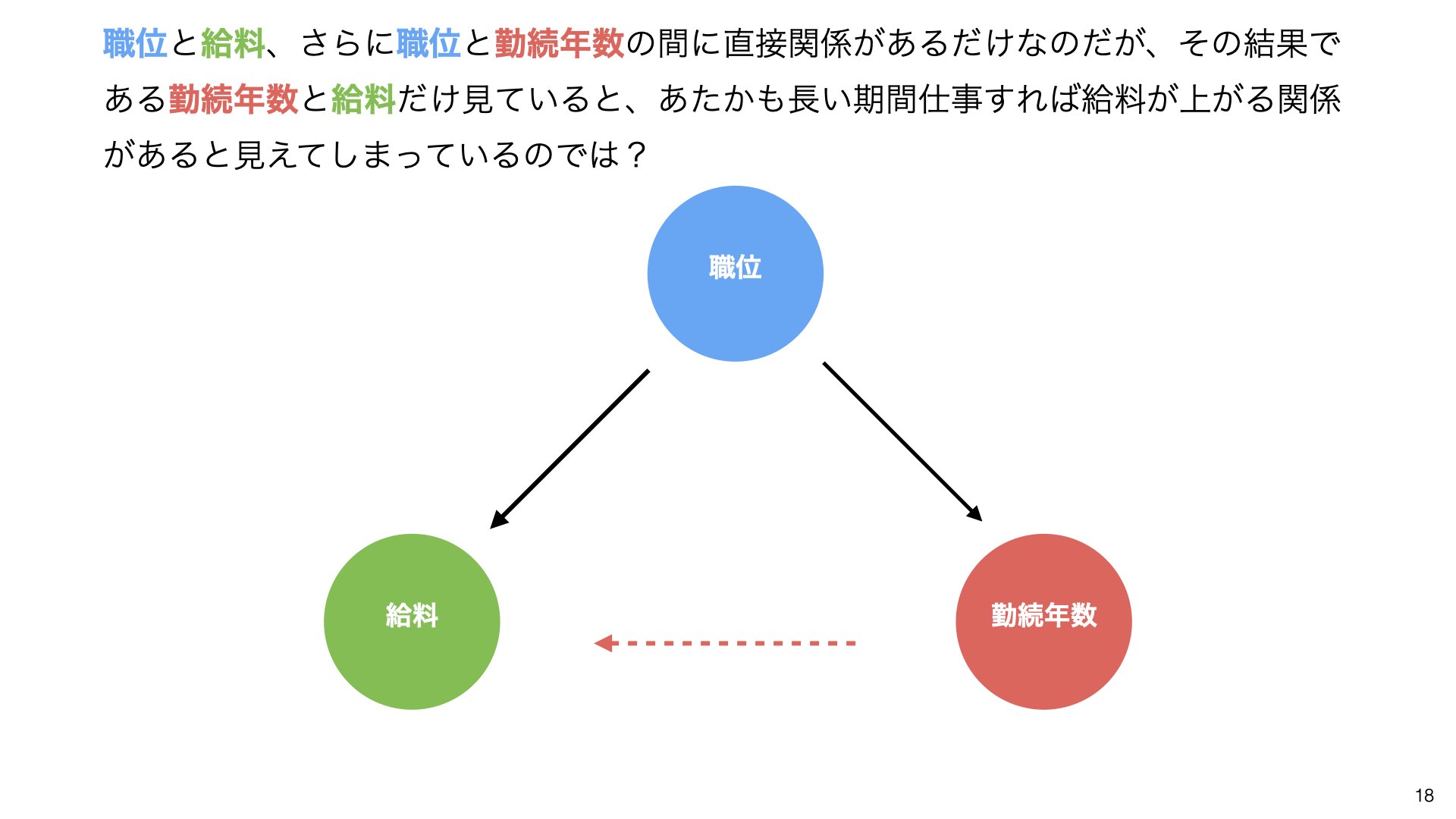
どちらが実際、給料に影響を与えているのでしょうか?
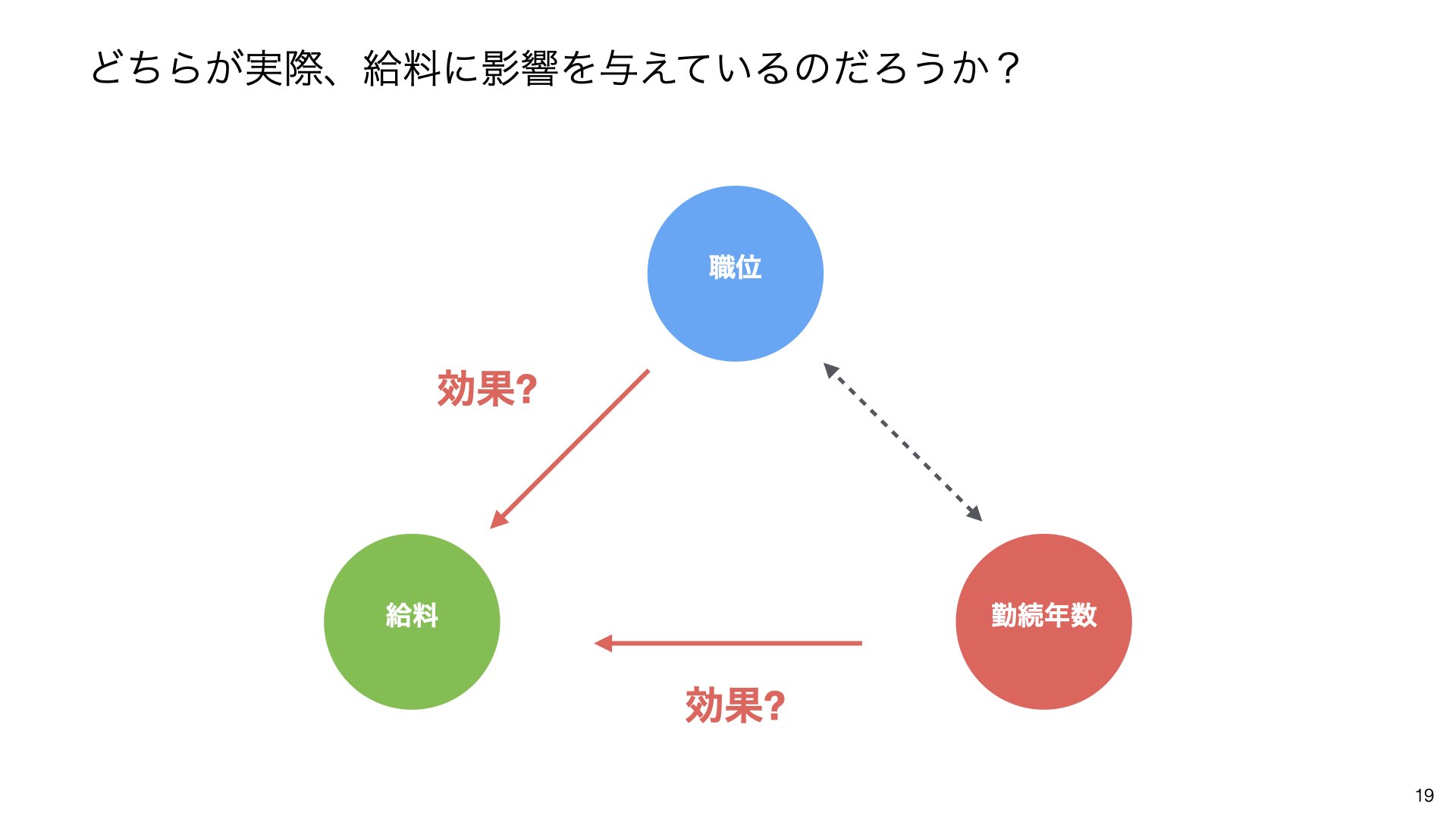
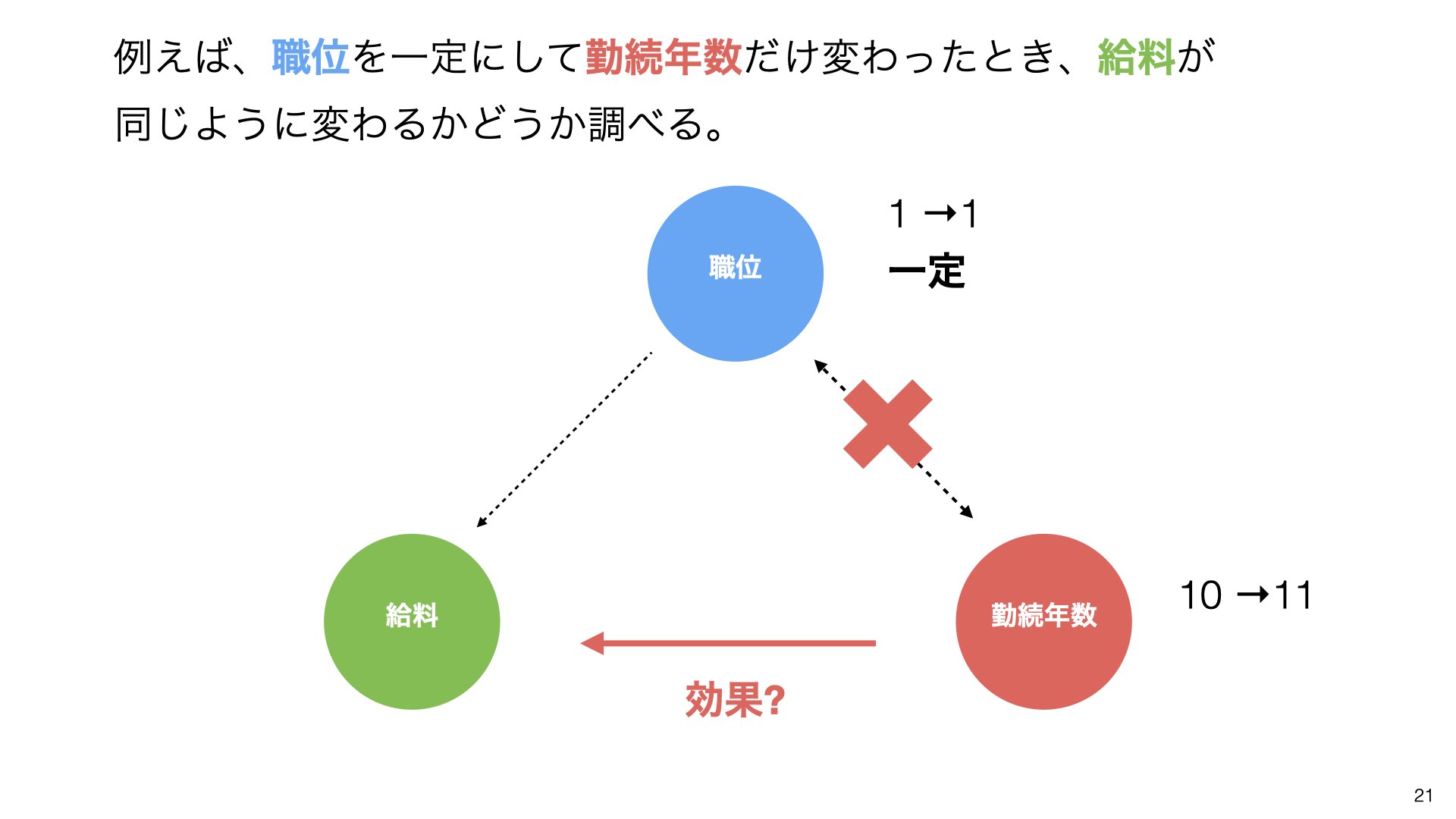
こういうときには、一つの変数のみを変化させて、他の変数を一定に保ったときに、それでも給料は変わるのかを調べればよいのです。
重回帰分析を行うことで、職位を一定にして勤続年数だけ変わったとき、給料が同じように変わるかどうか調べることができます。
逆に、職位の効果を知りたければ、勤続年数を一定にして職位だけ変わったとき、給料が変わるかどうかを調べることができます。
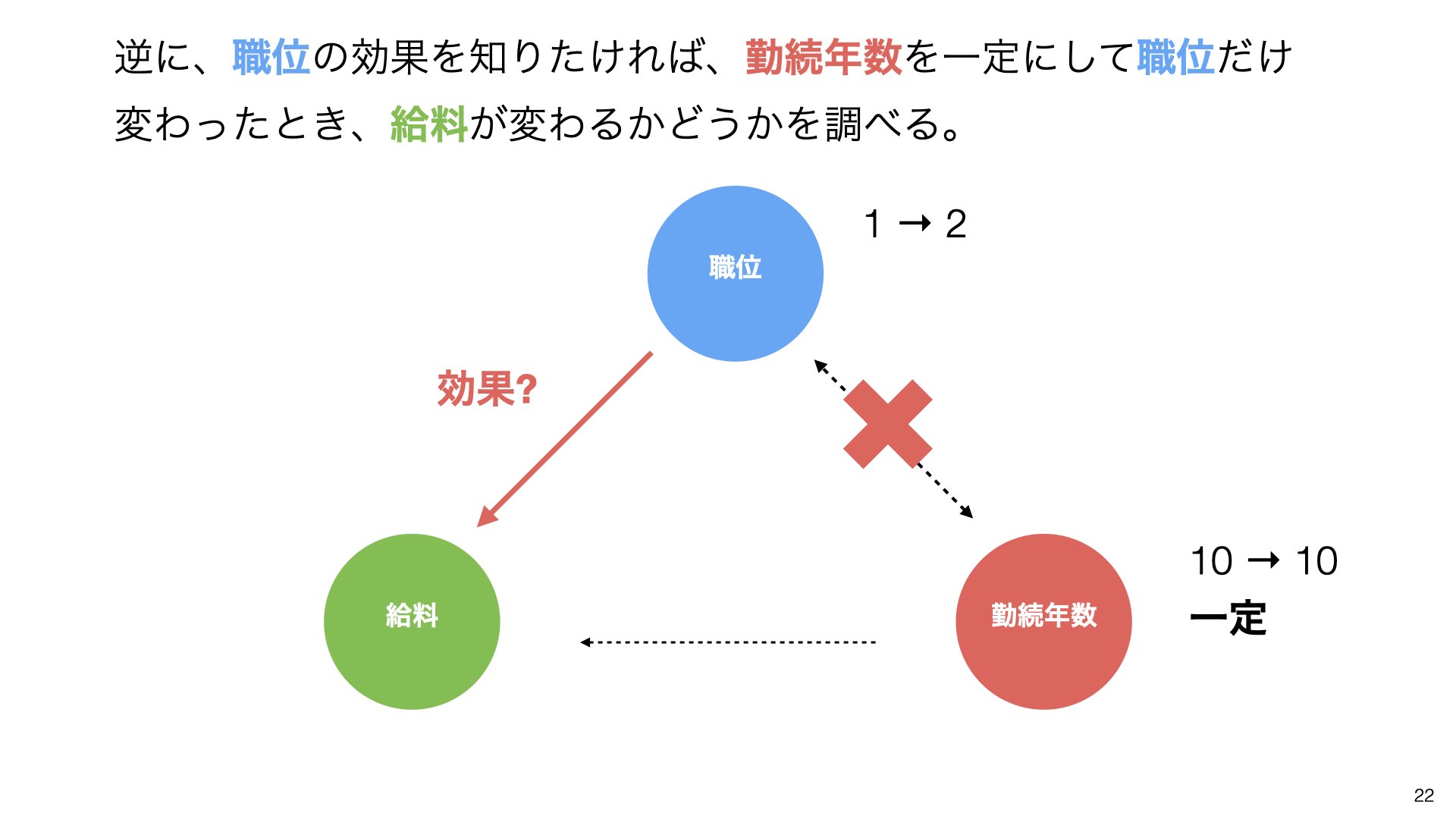
これが重回帰分析を使うメリットとなります。
単回帰と重回帰の計算式
単回帰の式
単回帰では、予測対象値(y)を一つの値(x)から予測する場合:
y = a × x + b給料の例では:
給料 = $500 × 勤続年数 + $5,000重回帰の式
重回帰では、予測対象の値(y)を複数の変数の値(x₁, x₂, …)から予測したい場合:
y = a₁ × x₁ + a₂ × x₂ + b給料の例では:
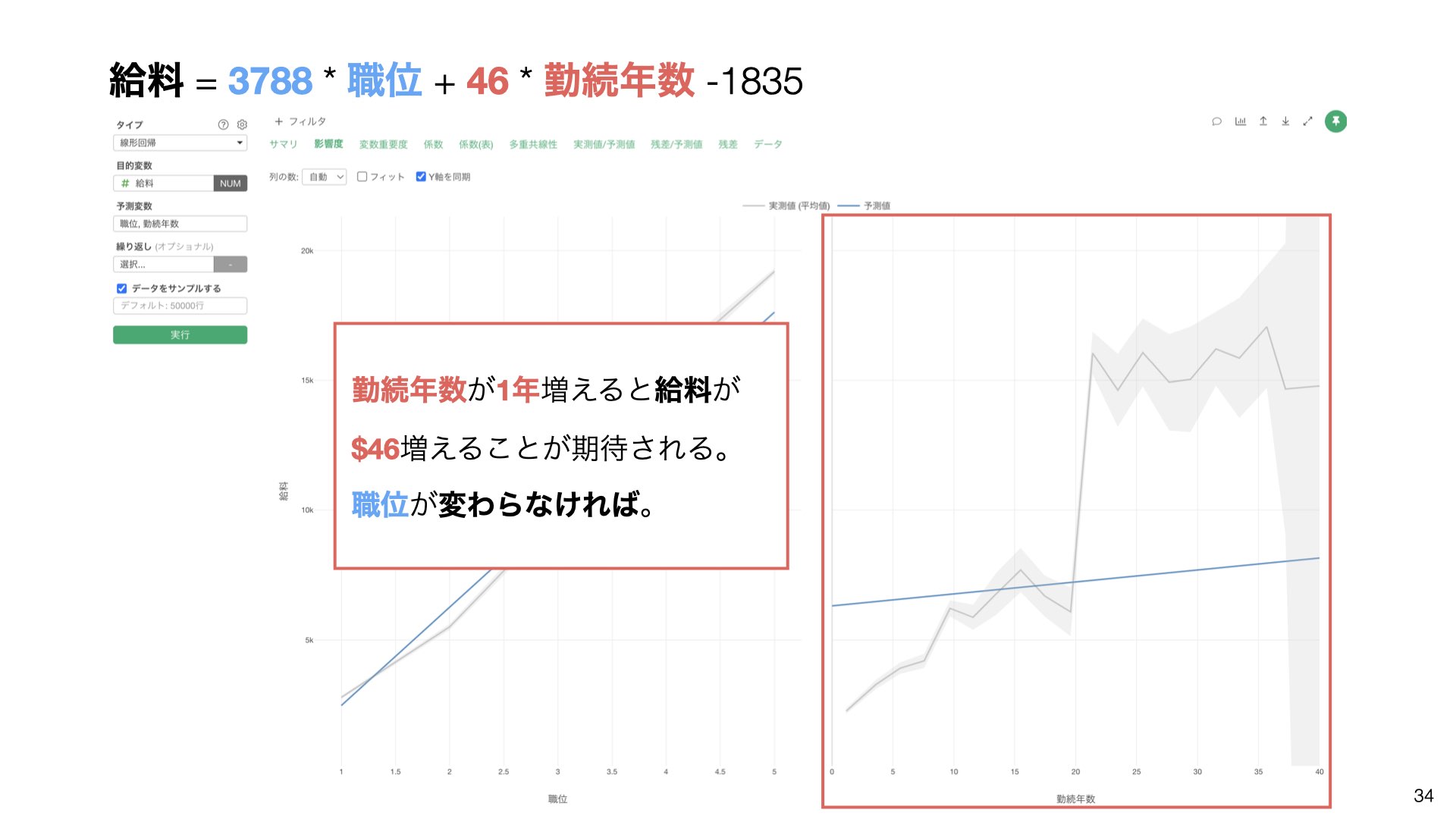
給料 = $500 × 勤続年数 + $600 × 職位 + $5,000重回帰分析の結果の解釈の例
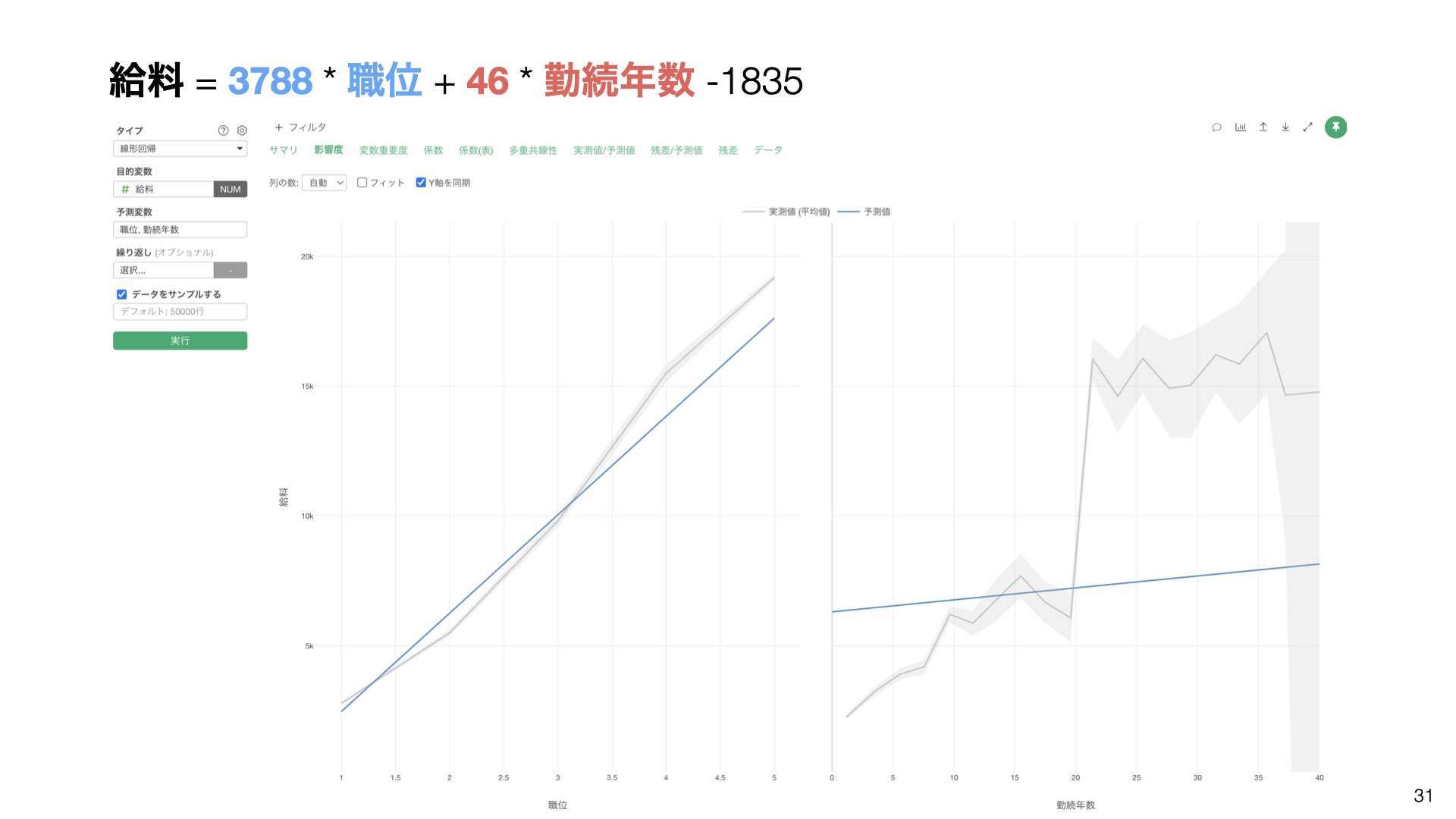
この式から読み取れることは:
職位が1つ上がると給料が$3,788上がることが期待される(勤続年数が変わらなければ)。
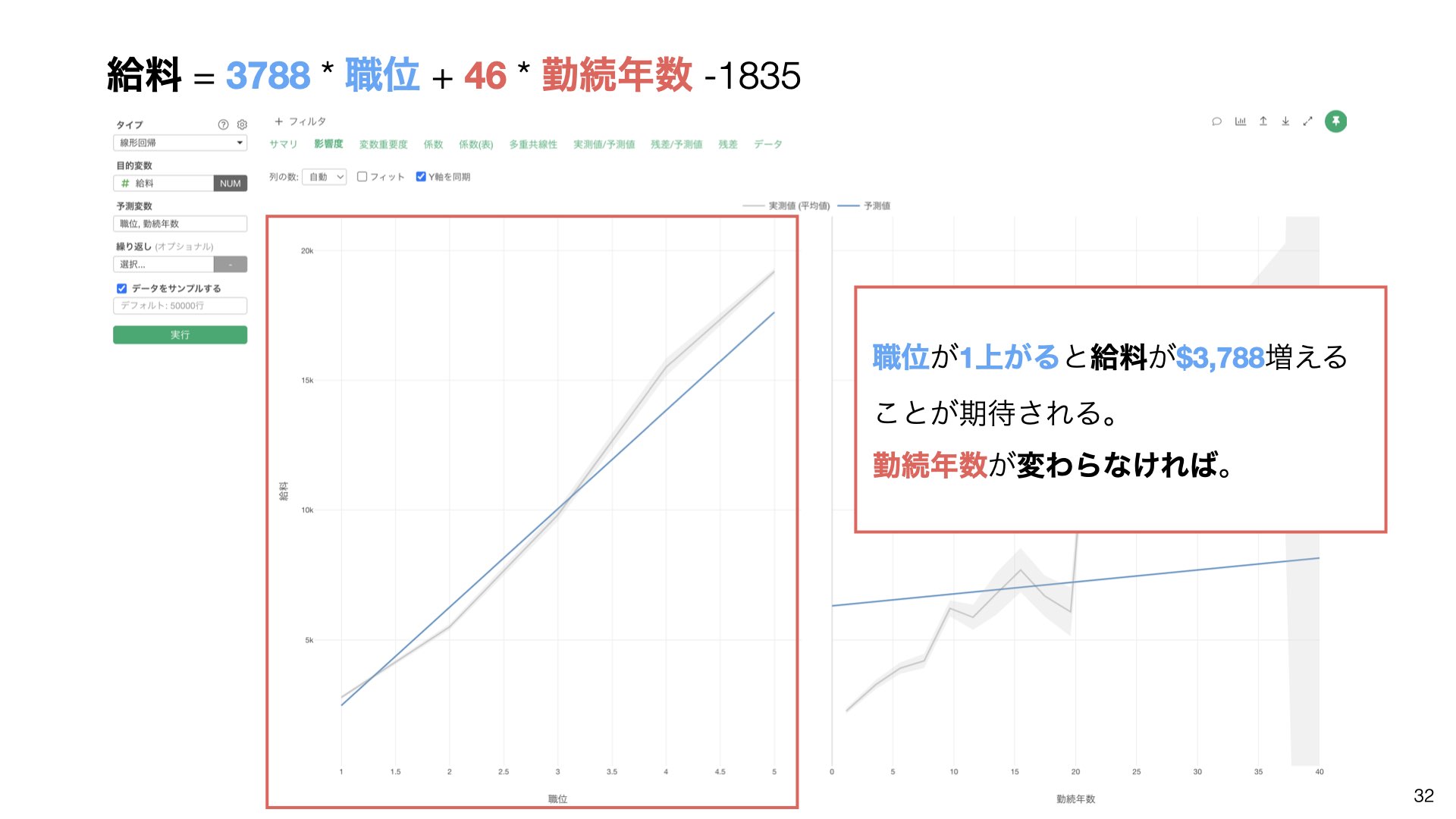
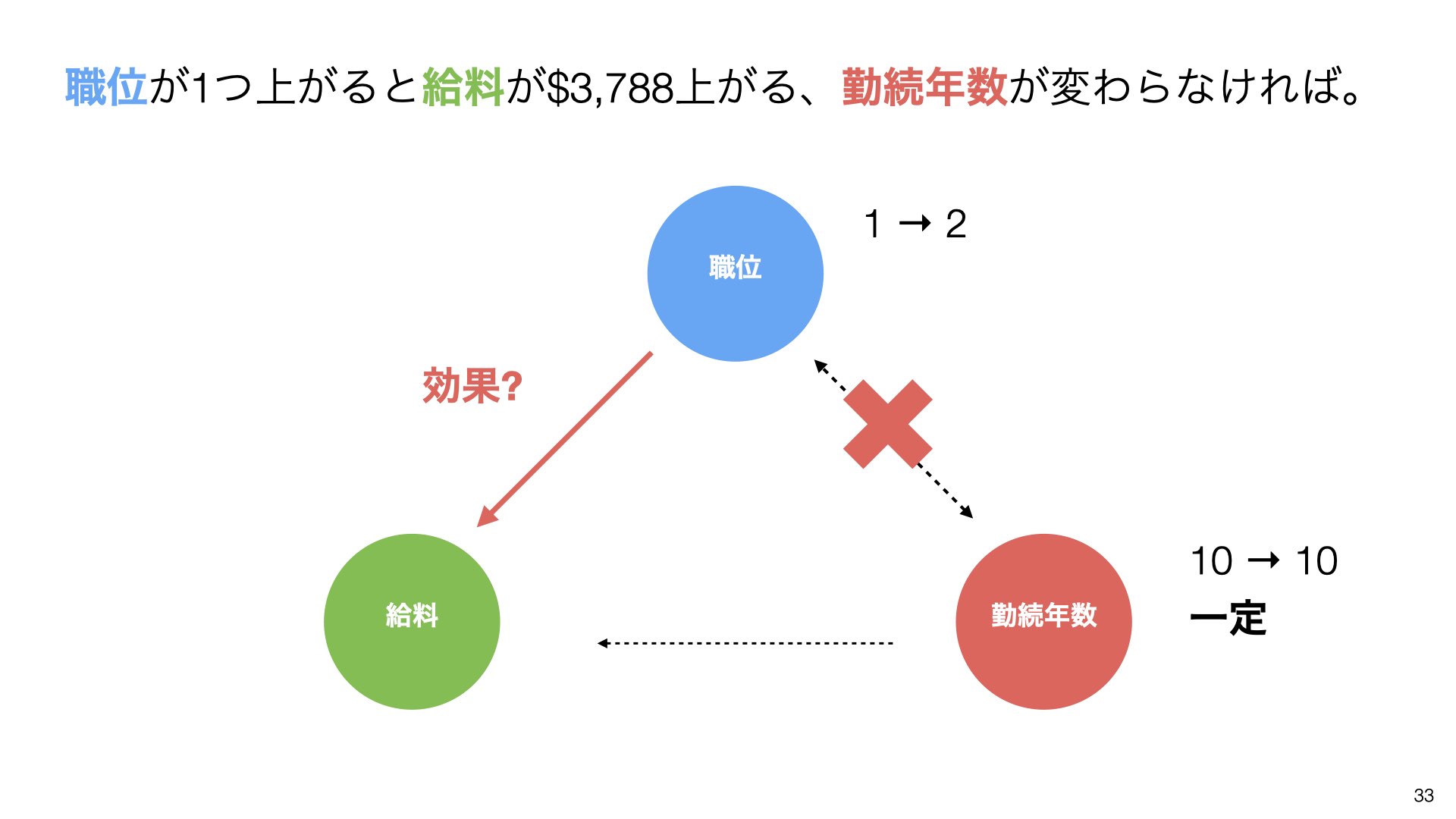
勤続年数が1年増えると給料が$46増えることが期待される(職位が変わらなければ)。
まとめ
単回帰と重回帰の違いは使用する説明変数の数にあり、単回帰は1つの変数から、重回帰は複数の変数から目的変数を予測します。
実際のデータでは複数の要因が結果に影響するため、重回帰が重要となります。例えば給料予測において、勤続年数と職位は両方とも給料と相関がありますが、これらの変数間にも相関があるため、どちらが真の影響要因かが不明確になります。
重回帰分析では他の変数を一定に保ちながら特定の変数の効果を測定できるため、各変数の独立した影響を正確に把握することが可能です。これにより、見かけ上の相関と因果関係を区別できます。