一般化線形モデル - GLM - 負の二項分布の使い方
一般化線形モデル(GLM)の負の二項分布は、0以上の整数(回数)データの分析において、特にばらつきが大きいデータを扱う際に適した統計手法です。世の中には「回数」として数えるデータが数多く存在します。このような回数データを分析する際に、データの特徴によって適切な分析手法を選ぶ必要があります。特に、極端に偏りの大きいデータを分析する時に効果的な手法が、GLM - 負の二項分布です。
少数の高い値と多数の低い値が混在する状況では、一般的な分析手法では正確な予測や要因分析が難しくなります。負の二項分布を使用した分析では、このような極端な偏りのあるデータでも、より正確に分析することができます。具体的には、それらに影響を与える要因を特定したり、将来の予測を行ったりすることが可能です。
このように、負の二項分布は、極端な偏りのあるデータに対して、より実態に即した分析を可能にする手法です。この分析結果を活用することで、より効果的なマーケティング施策の立案や、サービス改善のポイントを見つけることができます。
1. どういった時に使えるのか
GLM - 負の二項分布は、主にばらつきの大きい回数データを分析する際に使用します。
例えば、ECサイトでの商品レビュー数を考えてみましょう。人気商品には数百件ものレビューが付く一方で、大多数の商品にはほとんどレビューが付かないといった状況がよくあります。また、レストランの来店データでは、常連のお客様は月に何度も来店される一方で、たまにしか来ないお客様も多くいます。
商品の価格帯や商品説明の文字数、画像の数などが、実際にレビュー数にどの程度影響を与えているのかを明らかにしたり、新商品が出た際に、どの程度のレビュー数が集まりそうかを予測したりすることができます。また、顧客の来店回数、商品の不具合報告件数、ソーシャルメディアでの投稿数など、0以上の整数で表される回数データで、かつデータのばらつきが大きい現象の分析にも適しています。
参考となるデータ例:
- ECサイトの商品別レビュー数と関連指標(閲覧数、評価点、商品説明文字数など)
- 顧客の購買回数と顧客属性データ
- ウェブサイトの記事別コメント数と記事の特徴データ
- 店舗別の顧客苦情件数と店舗属性データ
2. ユースケース
Eコマース領域での使い方
- Eコマースでは、商品のレビュー数の予測や分析に使用できます。
- 具体的には、商品の特徴(価格帯、カテゴリー、商品説明の充実度)とレビュー数の関係を分析する際に負の二項分布GLMを使うことで、より精度の高い予測モデルを構築できます。
- これにより、レビュー獲得のための施策立案や、商品改善のポイントを特定することができます。
小売業領域での使い方
- 小売業では、店舗別の来客数や購買点数の分析に活用できます。
- 具体的には、店舗の立地条件や施策実施状況と来客数の関係を分析する際に使用することで、来客数の変動要因を特定できます。
- これにより、効果的な販促施策の立案や、店舗運営の改善施策を導き出せます。
マーケティング領域での使い方
- マーケティング領域では、キャンペーンやコンテンツの反応数の分析に使えます。
- 具体的には、コンテンツの特徴(種類、公開時間帯、長さ)と獲得できた反応数の関係を分析する際に使用することで、効果的なコンテンツの特徴を把握できます。
- これにより、より高い反応が得られるコンテンツ戦略の立案が可能となります。
カスタマーサポート領域での使い方
- カスタマーサポート領域では、問い合わせ件数の分析に活用できます。
- 具体的には、商品カテゴリーや時期、顧客属性と問い合わせ件数の関係を分析する際に使用することで、問い合わせ増加の要因を特定できます。
- これにより、サポート体制の最適化や、予防的な対策の立案が可能となります。
3. ExploratoryでGLM - 負の二項分布を実行する
使用するデータ
今回は「ECサイトのレビューデータ」を使用します。データはこちらからダウンロードが可能となっています。
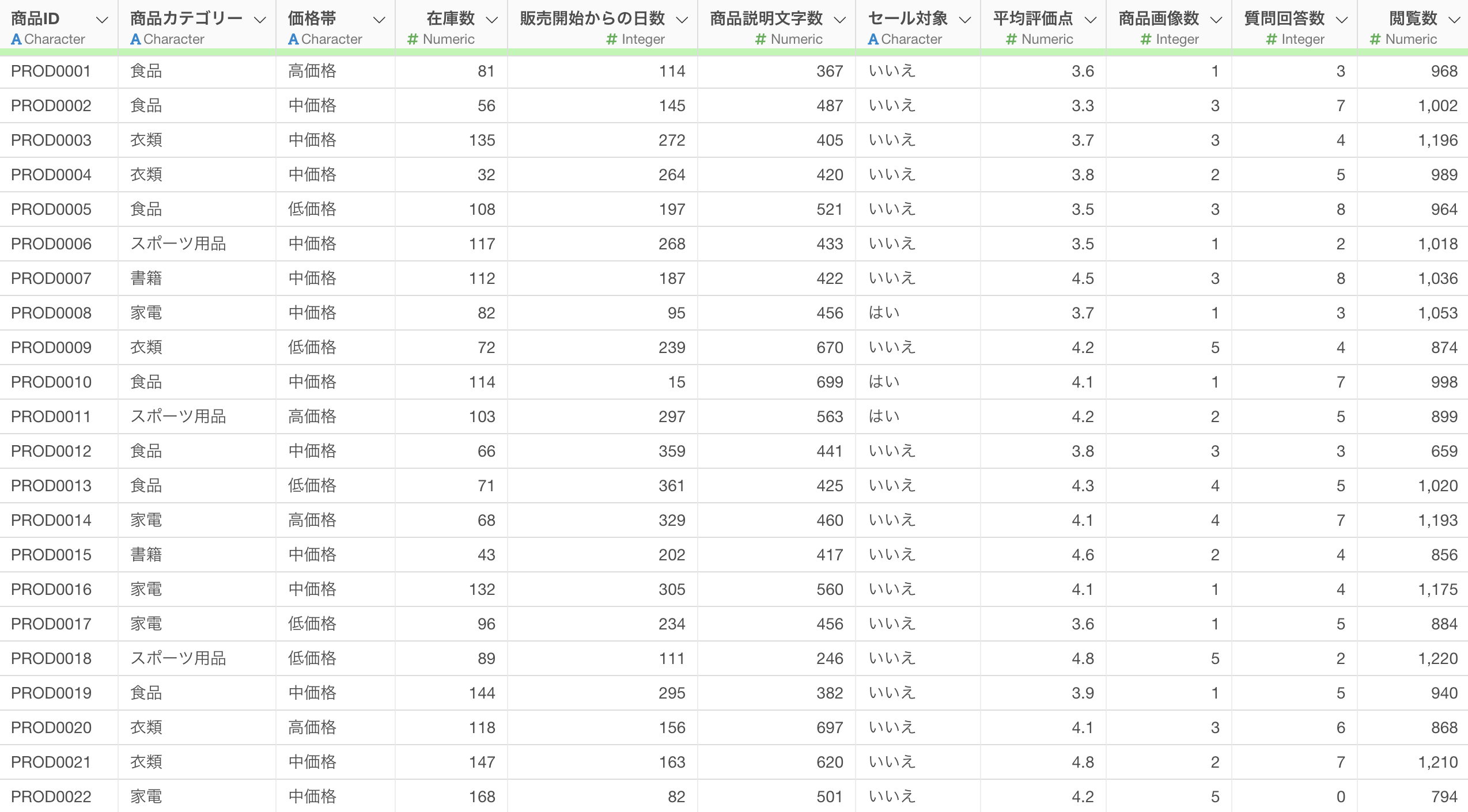
このデータは1行が1商品を表し、ECサイトでの商品別のレビュー数とその関連指標(価格帯、カテゴリー)などの情報が列としてあります。
GLM - 負の二項分布を実行するためには、以下のようなデータの構造が必要となります。
- 目的変数は非負の整数値(カウントデータ)である必要があります
- 目的変数の分散が平均よりも大きい(過分散)特徴を持つ必要があります
- 予測変数は数値型もしくはカテゴリ型である必要があります
- データに欠損値が含まれていないことが望ましいです
アナリティクスを作成する
ECサイトのレビューデータから「アナリティクス・ビュー」を開きます。
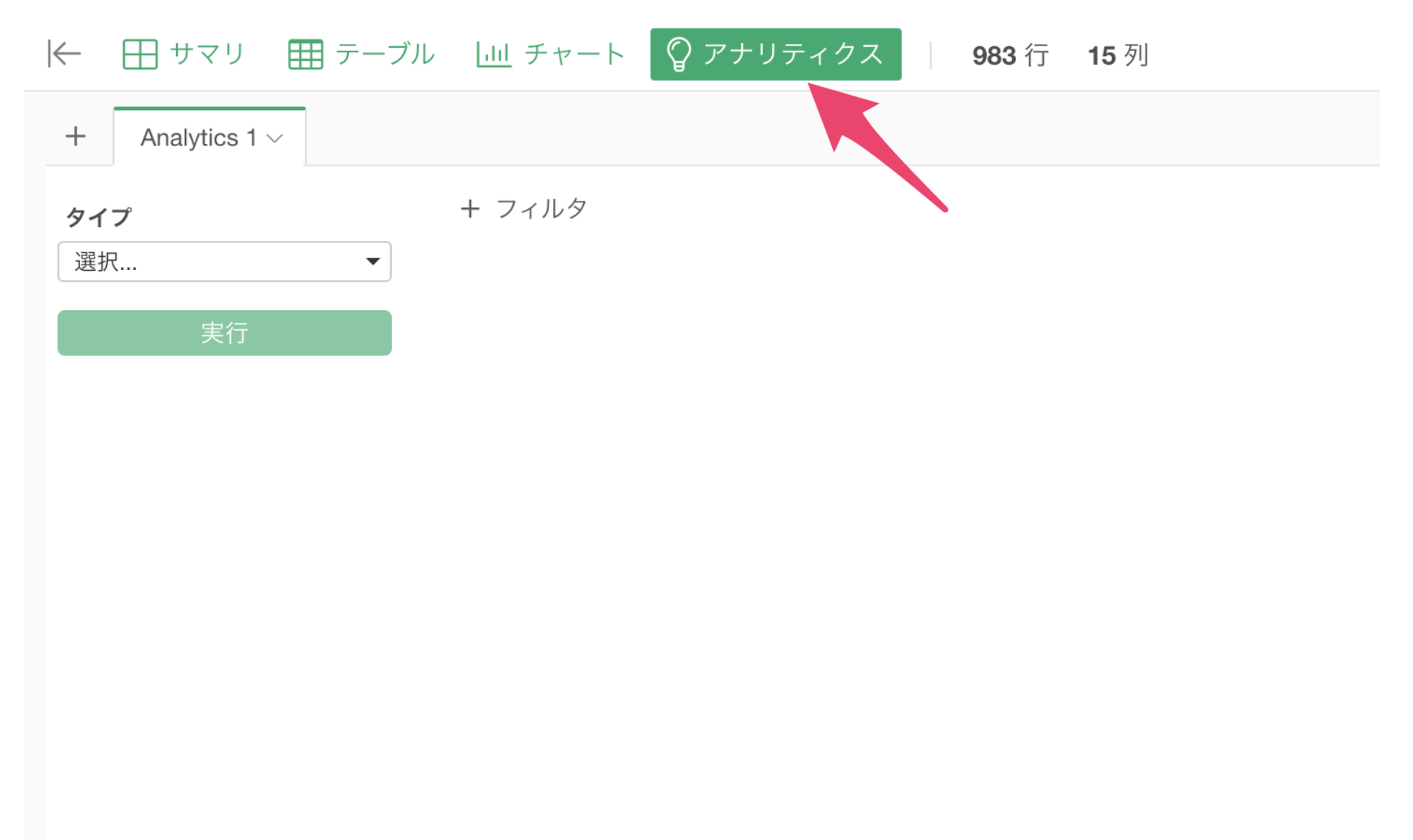
タイプに「一般化線形モデル」を選び、「GLM - 負の二項分布」を選択します。
目的変数には、「レビュー数」の列を割り当てます。
予測変数には、「商品カテゴリー」から「購入数」までの列をシフトキーを押しながら複数選択します。
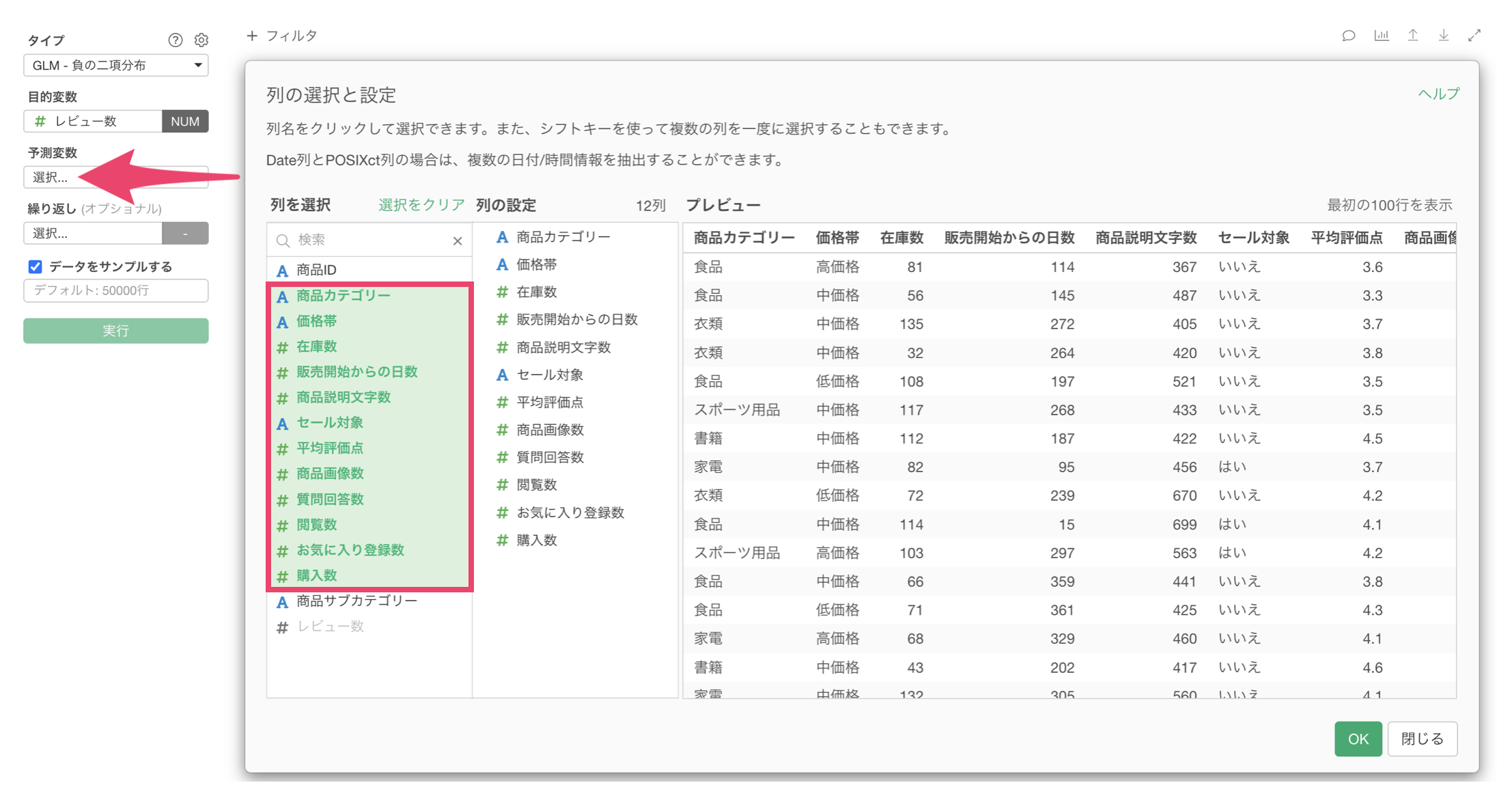
最後に、「実行」ボタンをクリックして実行結果を確認します。
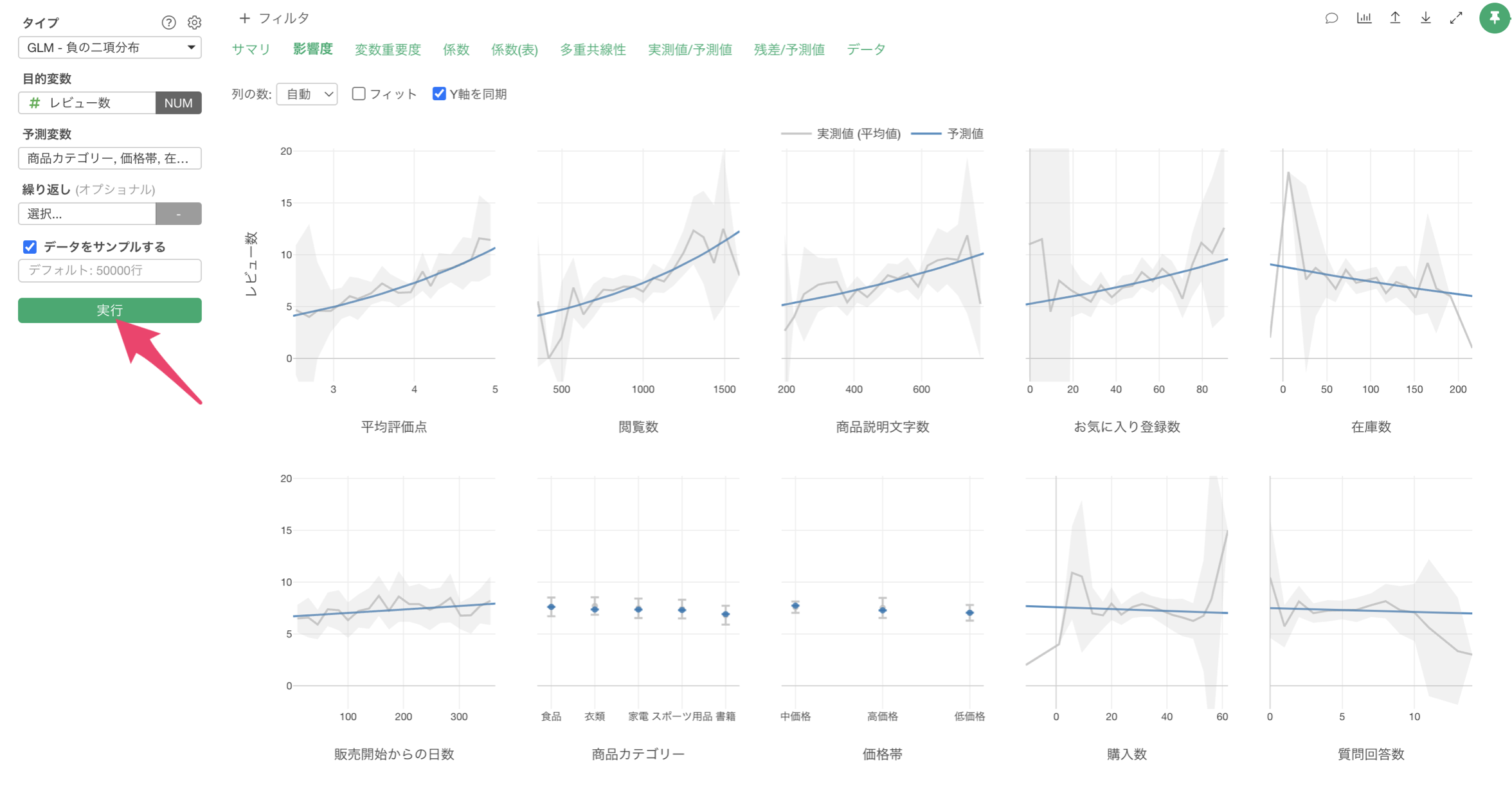
結果の解釈
GLM - 負の二項分布では、レビュー数に影響を与える要因を解釈するために変数重要度や影響度などの情報があります。
多重共線性
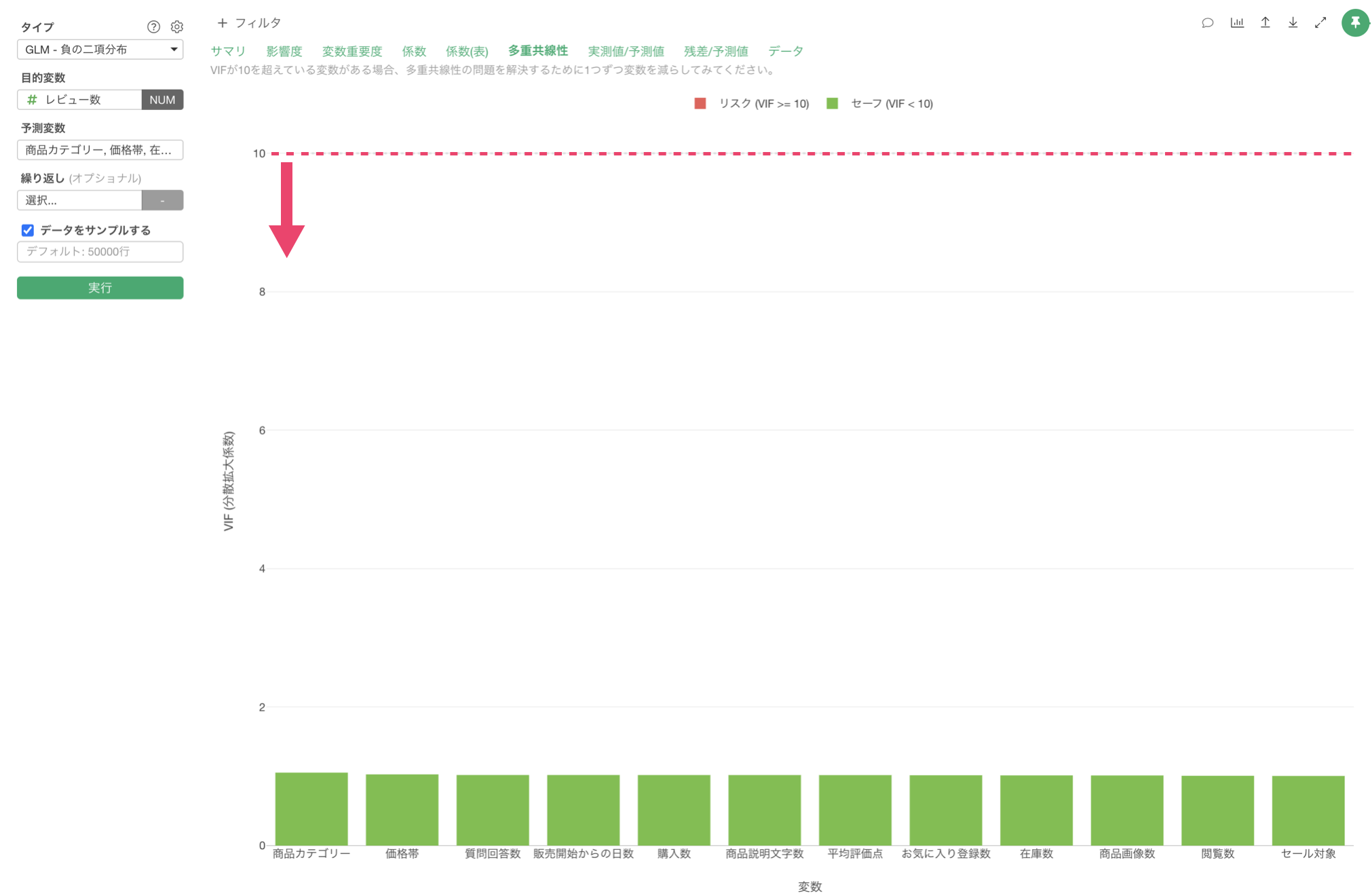
「多重共線性」タブをクリックすると、予測変数間の相関が強すぎる(VIF > 10)組み合わせがないかを確認できます。VIFが10以上の変数がある場合、モデルの信頼性に影響を与える(傾きが不安定になる)可能性があるため、変数の選択を見直す必要があります。
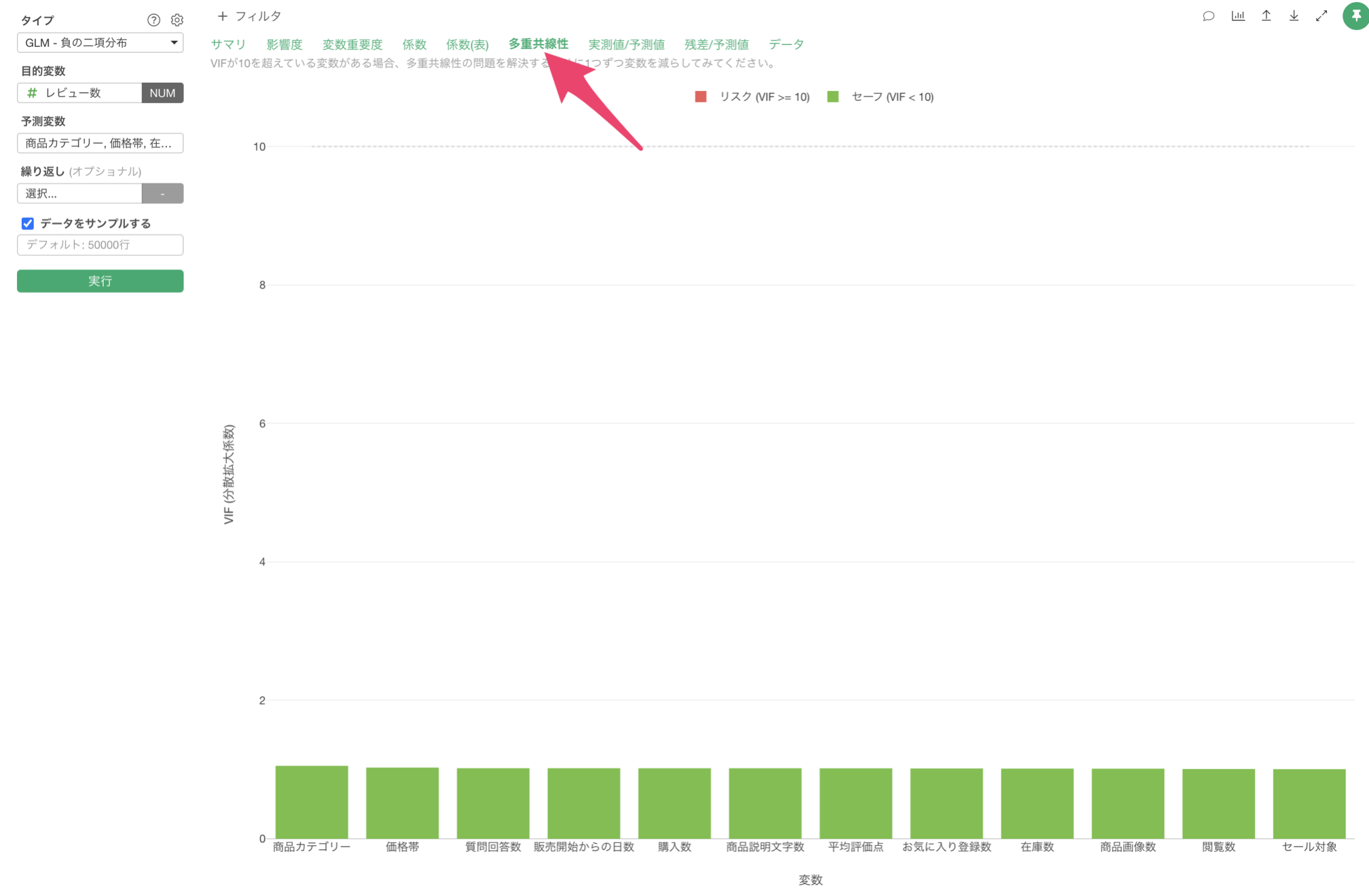
今回の結果は、VIFが10以上のものはないため、予測変数同士に相関が強すぎる変数の組み合わせがないため、モデルが不安定であることはないことがわかります。
変数重要度
「変数重要度」タブをクリックすると、目的変数を予測する上でどの変数が重要なのかを確認することができます。
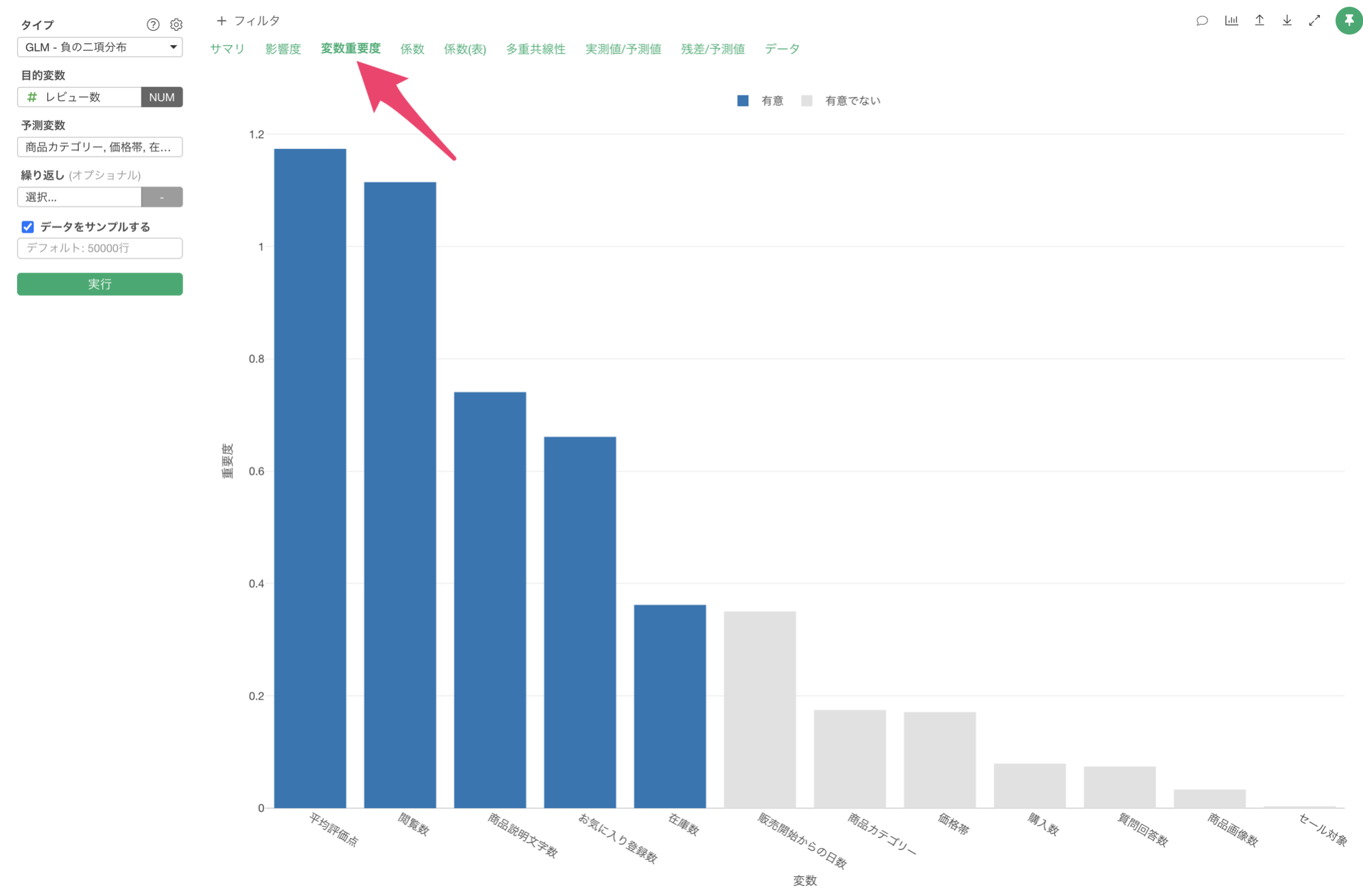
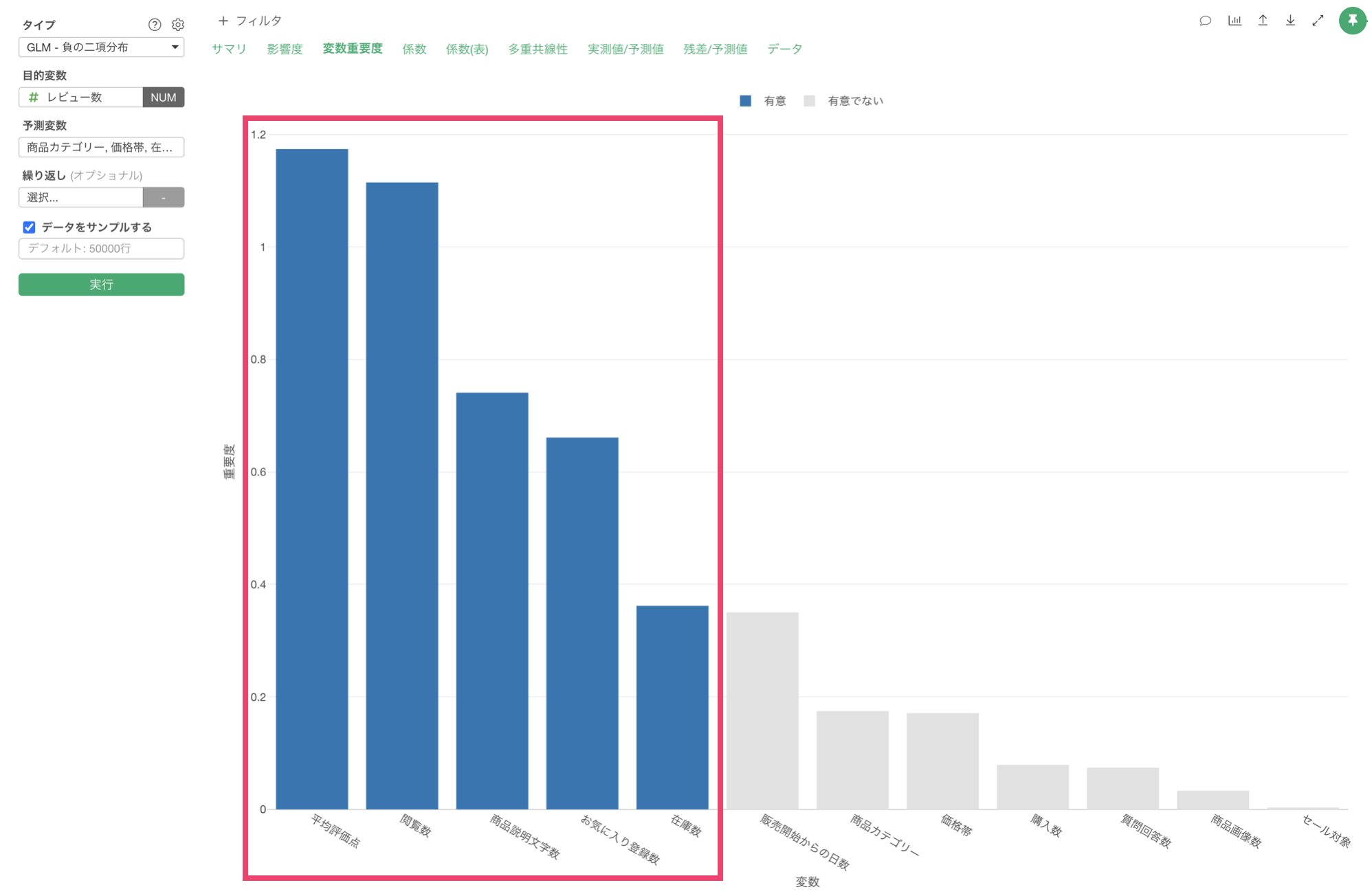
この結果から、レビュー数の予測に最も重要な変数は平均評価点であり、次いで閲覧数、商品説明文字数の順となっていることがわかります。これは、商品の評価の高さや閲覧数がレビュー数に大きく影響していることを示しています。
影響度
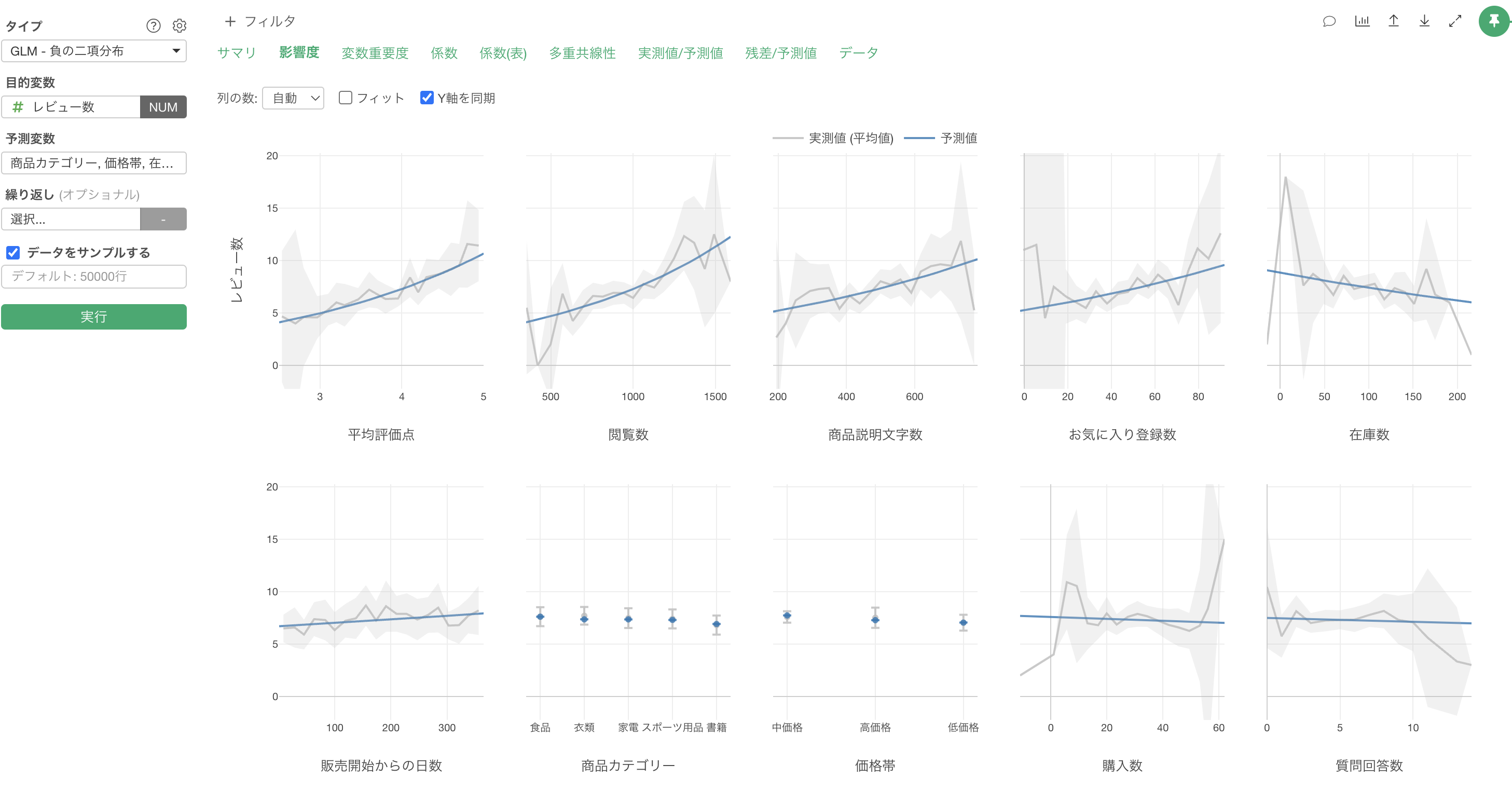
「影響度」タブをクリックすると、各予測変数がレビュー数に与える影響の方向と強さを確認することができます。
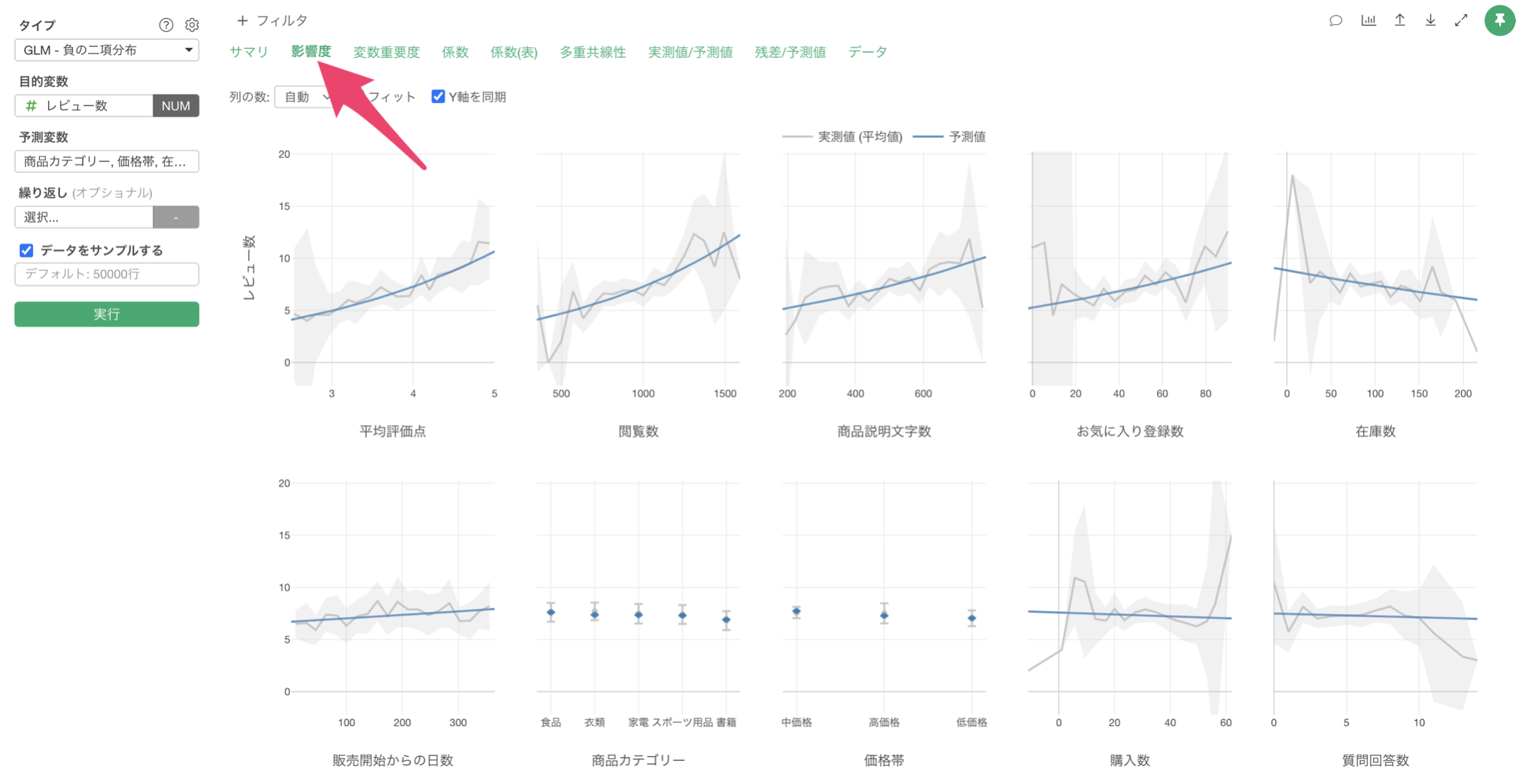
例えば、平均評価点の値が上がると、レビュー数も増えることが確認出来ます。
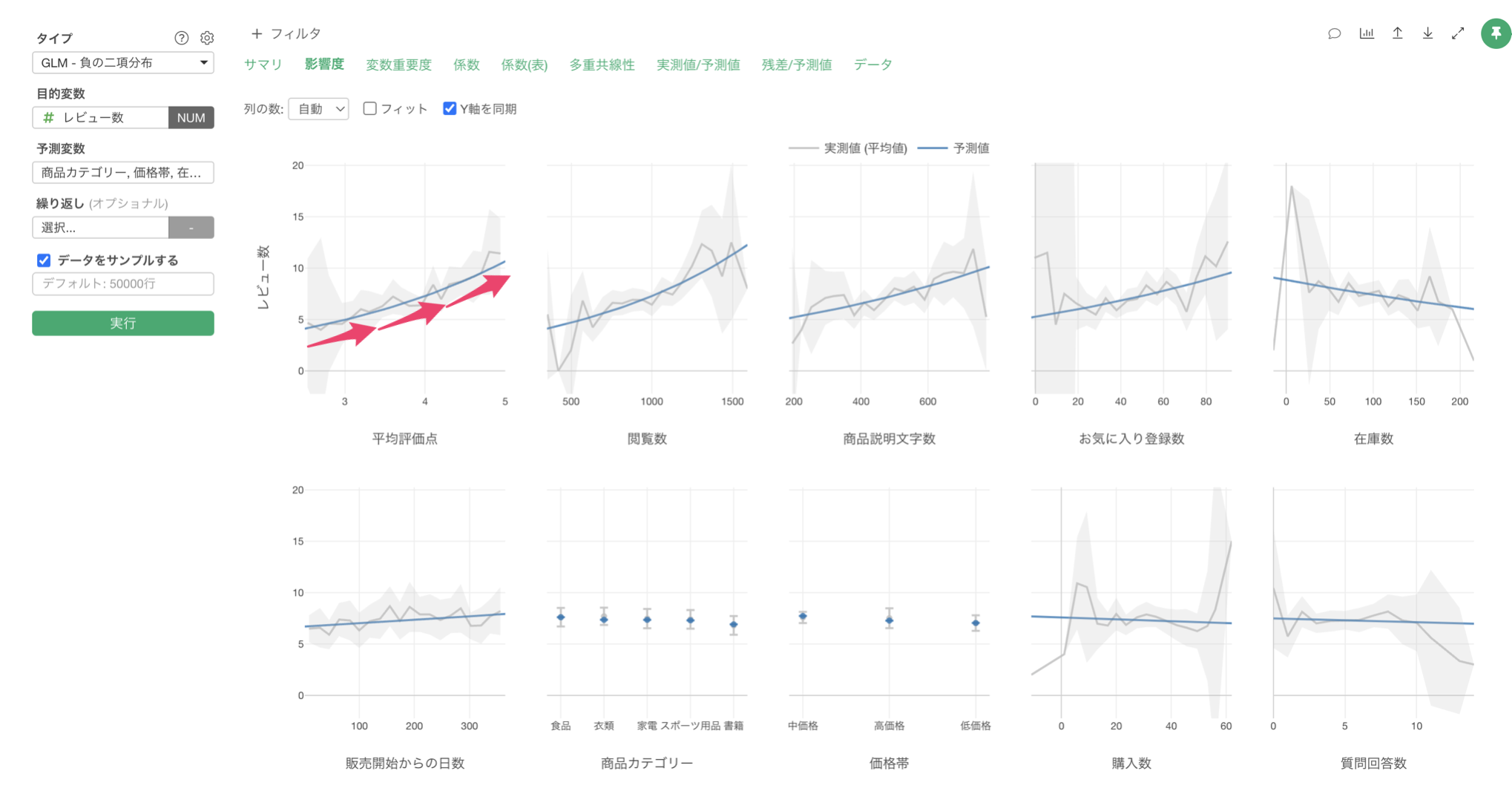
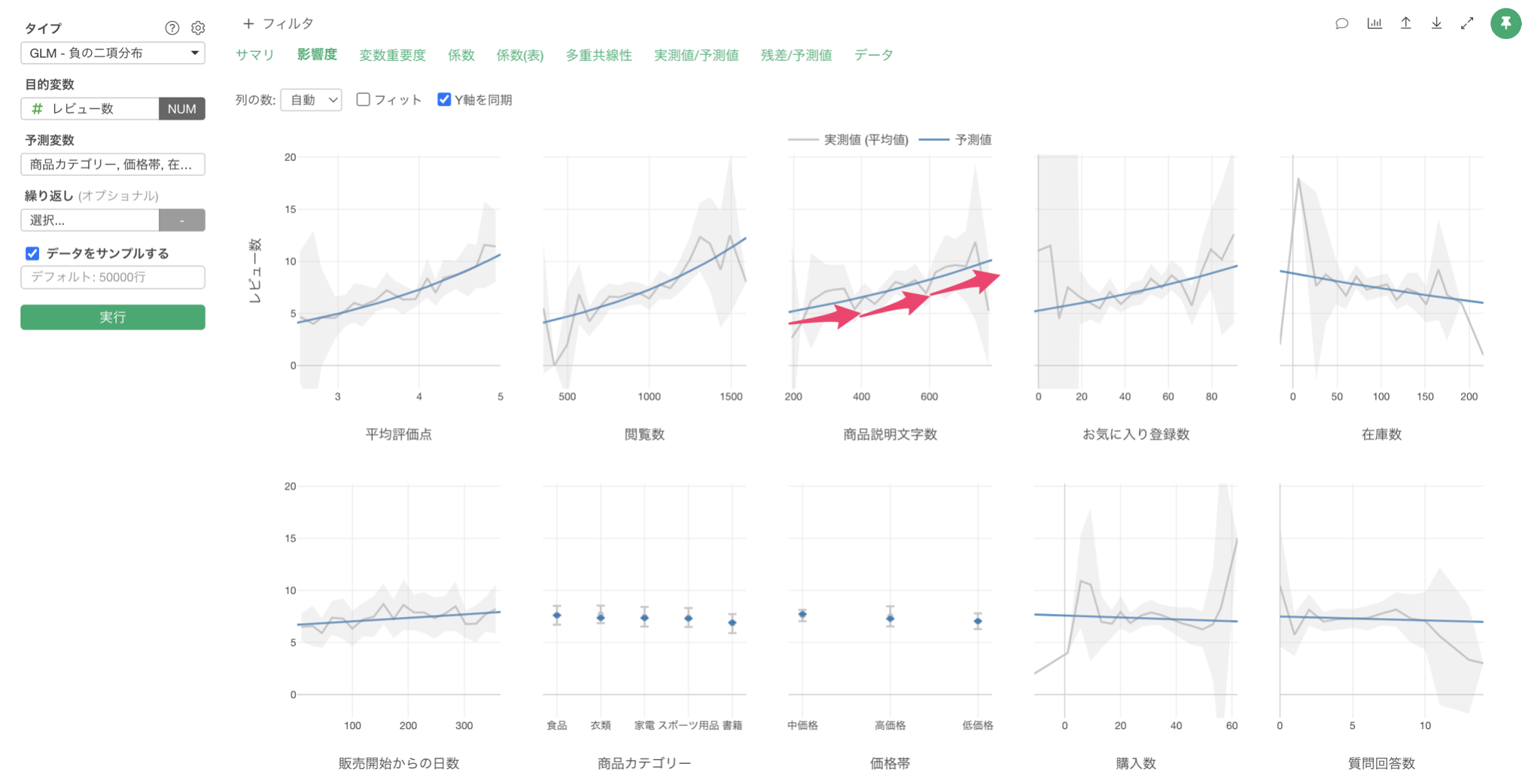
また、商品説明文字数が長くなればなるほど、レビュー数の評価も増える関係があることがわかります。商品説明が充実していることで、顧客の期待値と実際の商品との差異が小さくなり、満足度が高くなり、結果的にレビュー数が増えているのかもしれません。
係数
「係数」タブをクリックすると、各予測変数の係数とその統計的有意性を確認することができます。
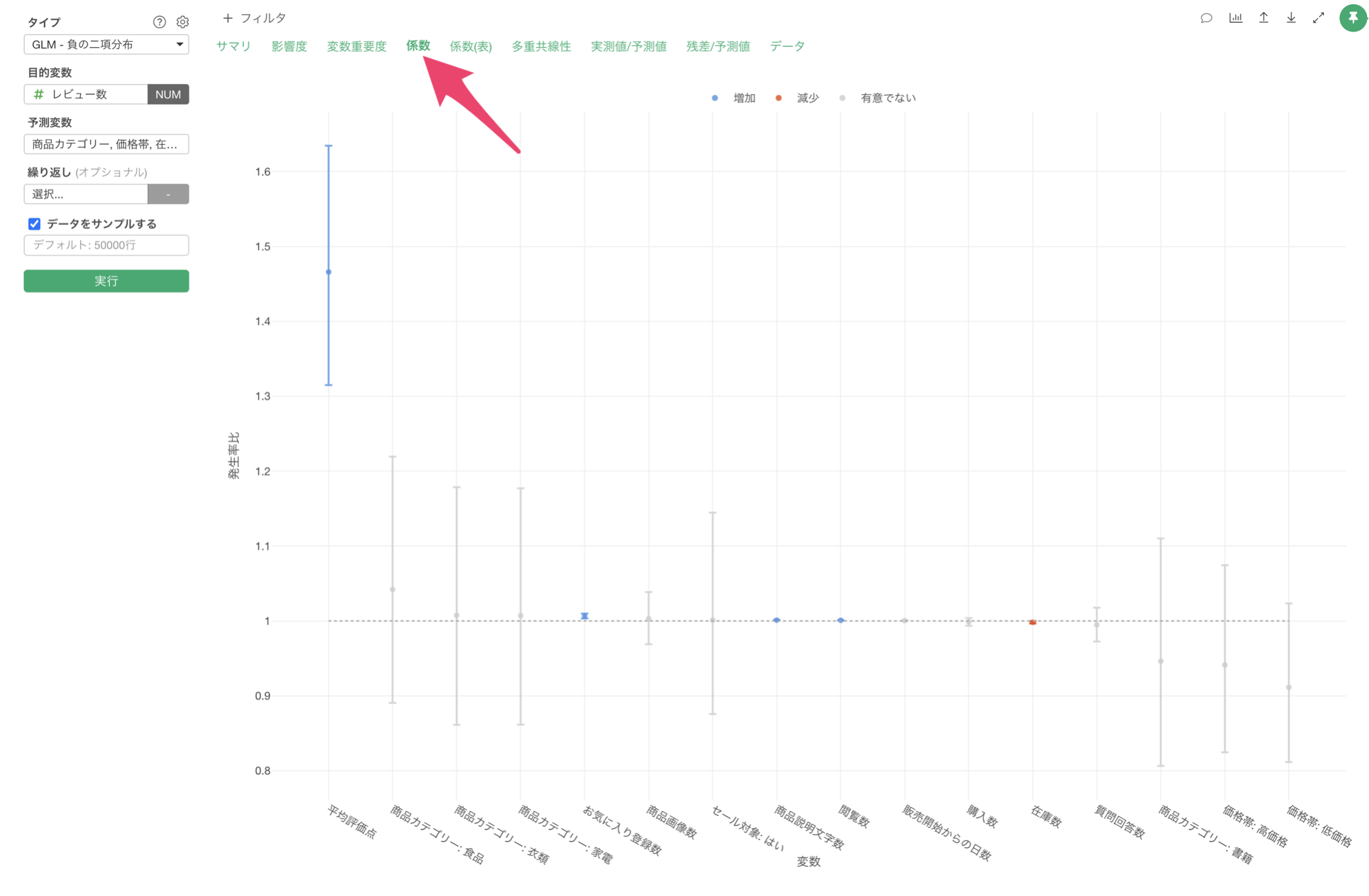
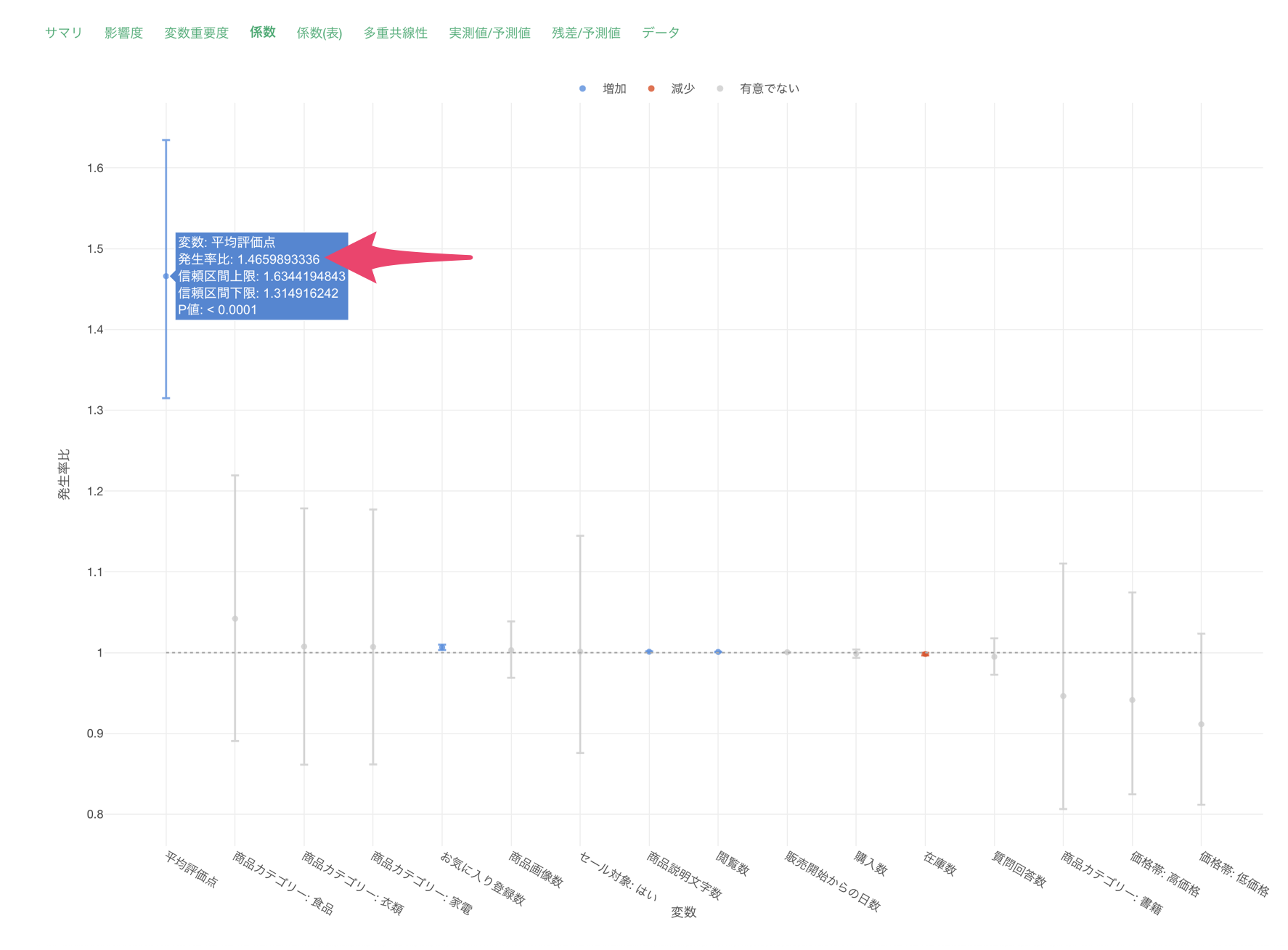
この結果から、各変数の効果の大きさと方向性を具体的な数値で確認できます。係数(発生率比)が正の値は、その変数が増加するとレビュー数も増加することを示し、負の値は減少することを示します。P値が0.05未満の変数は、統計的に有意な影響を持っていると判断できます。
例えば、平均評価点が1点上がると、発生率比が1.465のためレビュー数が1.465倍になる傾向があると解釈が出来ます。P値も0.0001未満のため、統計的に有意な関係があると判断が出来ます。
サマリ
「サマリ」タブをクリックすると、モデル全体の予測精度を確認することができます。
 Thetaの解釈
Thetaの解釈
Theta(θ)は、データのばらつきの大きさを示す指標です。値が大きいほど安定したデータ、小さいほどばらつきが大きいことを示します。
基準値:
- 2以上:安定している
- 1-2:適度なばらつき
- 1未満:ばらつきが大きい(注意が必要)
今回の結果(θ = 2.06)は2を超えており、データが比較的安定していることを示しています。
逸脱度の減少率
モデルがデータをどれだけ上手く説明できているかを示す指標です。値が大きいほど、モデルの説明力が高いことを意味します。
逸脱度減少率=Nullモデルの逸脱度−残差逸脱度Nullモデルの逸脱度×100 = 100逸脱度減少率=Nullモデルの逸脱度Nullモデルの逸脱度−残差逸脱度×100
基準値:
- 20%以上:とても良い
- 10-20%:十分な改善
- 5-10%:ある程度の改善
- 5%未満:改善が小さい
今回の場合は以下のように計算ができ、11.8%の減少は、十分な改善が見られたことを示しています。
(1247.66 - 1099.85) / 1247.66 × 100 = 11.8%4. まとめ
GLM - 負の二項分布は、レビュー数、来店回数、問い合わせ件数といった「回数」を分析する際に、特に極端な偏りがあるデータに対して効果的な分析手法です。
今回のECサイトのレビュー数分析では、レビュー数に影響を与える主な要因として、平均評価点、閲覧数、商品説明文字数が関係があることがわかりました。これらの分析結果から、レビュー数を増やすためには、商品の評価を高める取り組み、商品説明の充実化などが効果的だと考えられます。