外れ値検知の方法
外れ値検知とは、データの標準的な分布から大きく離れた値(外れ値)を見つけ出す手法です。外れ値は、測定ミスや記入ミスなどのエラーが原因であったり、実際に異常な値である場合があります。
下記の図のように、多くのデータ(緑色の人々)は正規分布のように中央付近に集まっていますが、右端にある赤い人のように、他のデータから大きく外れた値が外れ値です。
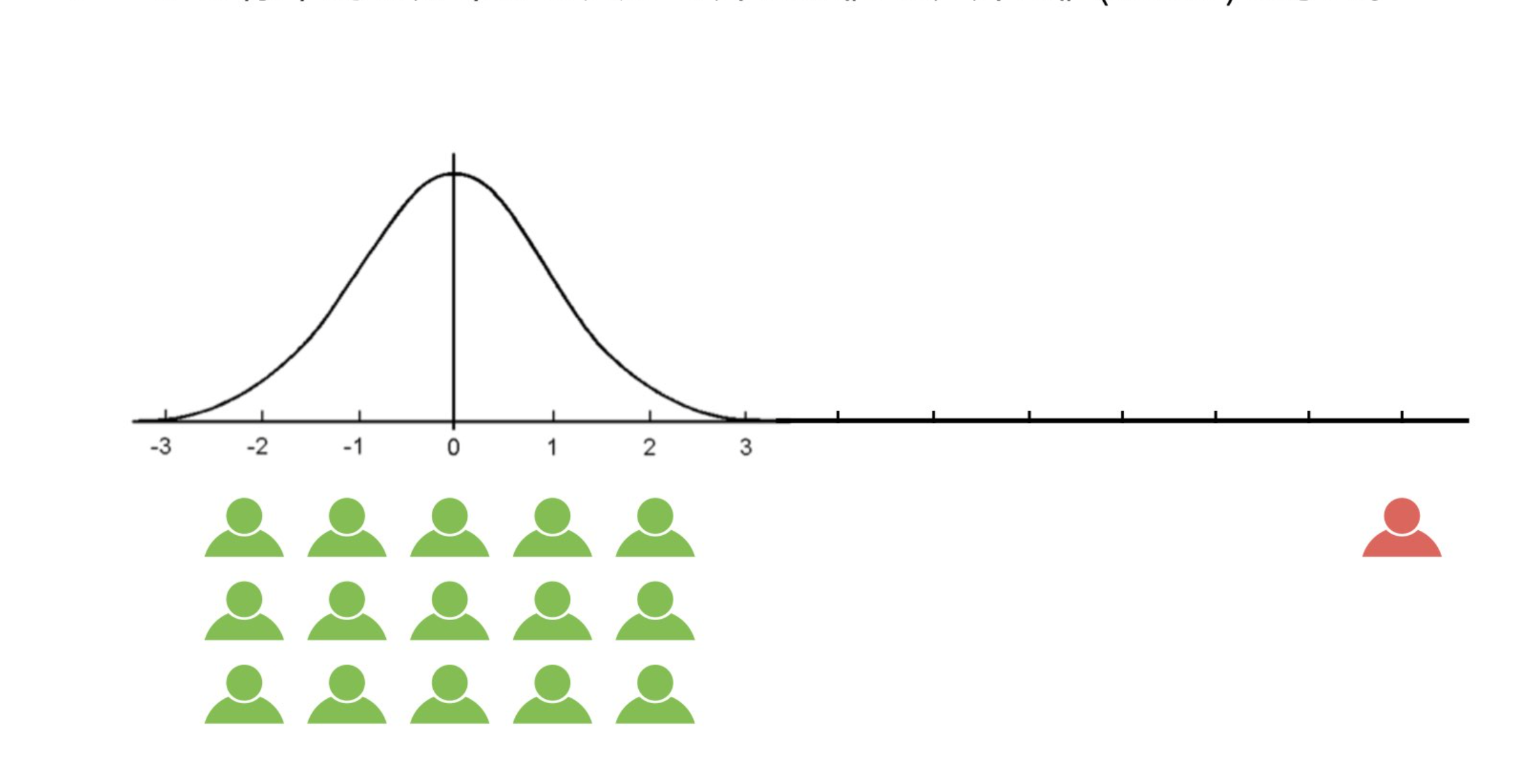
外れ値検知の基本的な考え方
外れ値があると、以下のような問題が発生します。
そもそも間違ったデータかもしれない
データの中にあるパターンが掴めなくなる
外れ値の影響を受けて相関関係の解釈が変わってしまう
例えば、下の図は外れ値がある場合(左)とない場合(右)の散布図を比較したものです。外れ値があると、相関係数が0.188と低くなりますが、外れ値を除くと相関係数が0.598と高くなります。このように、外れ値は分析結果に大きな影響を与えるのです。
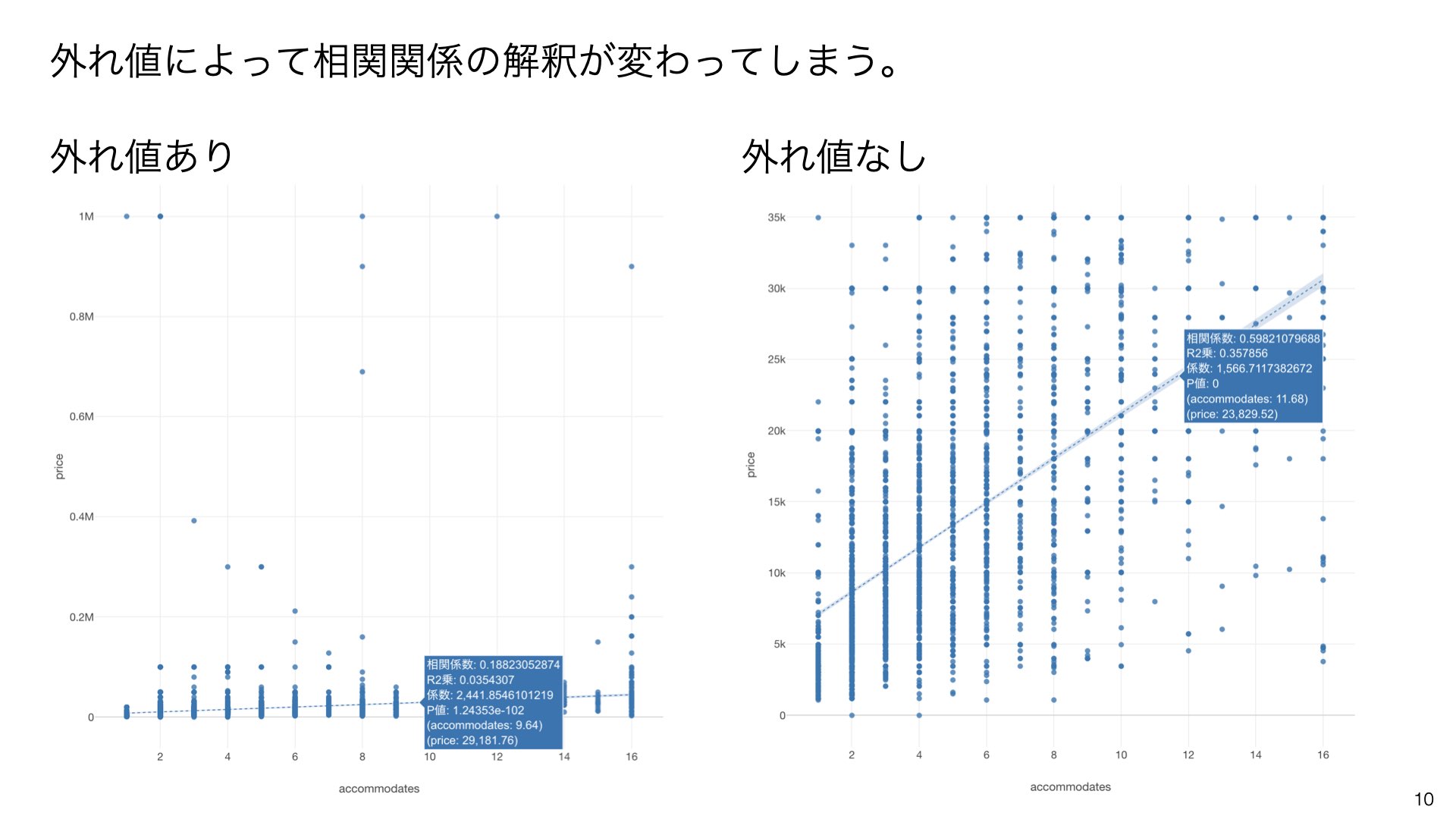
外れ値検知の主要な手法
外れ値検知には主に3つのタイプがあります:
標準偏差を使った方法
パーセンタイルを使った方法
IQR(四分位範囲)を使った方法
実際の外れ値検知の計算例
1. 標準偏差を使った外れ値検知
標準偏差とは、データのばらつきの平均を表す値で、偏差値を計算する際に使用されています。
標準偏差の性質を利用して、指定した標準偏差の外にあるデータを外れ値とすることができます。
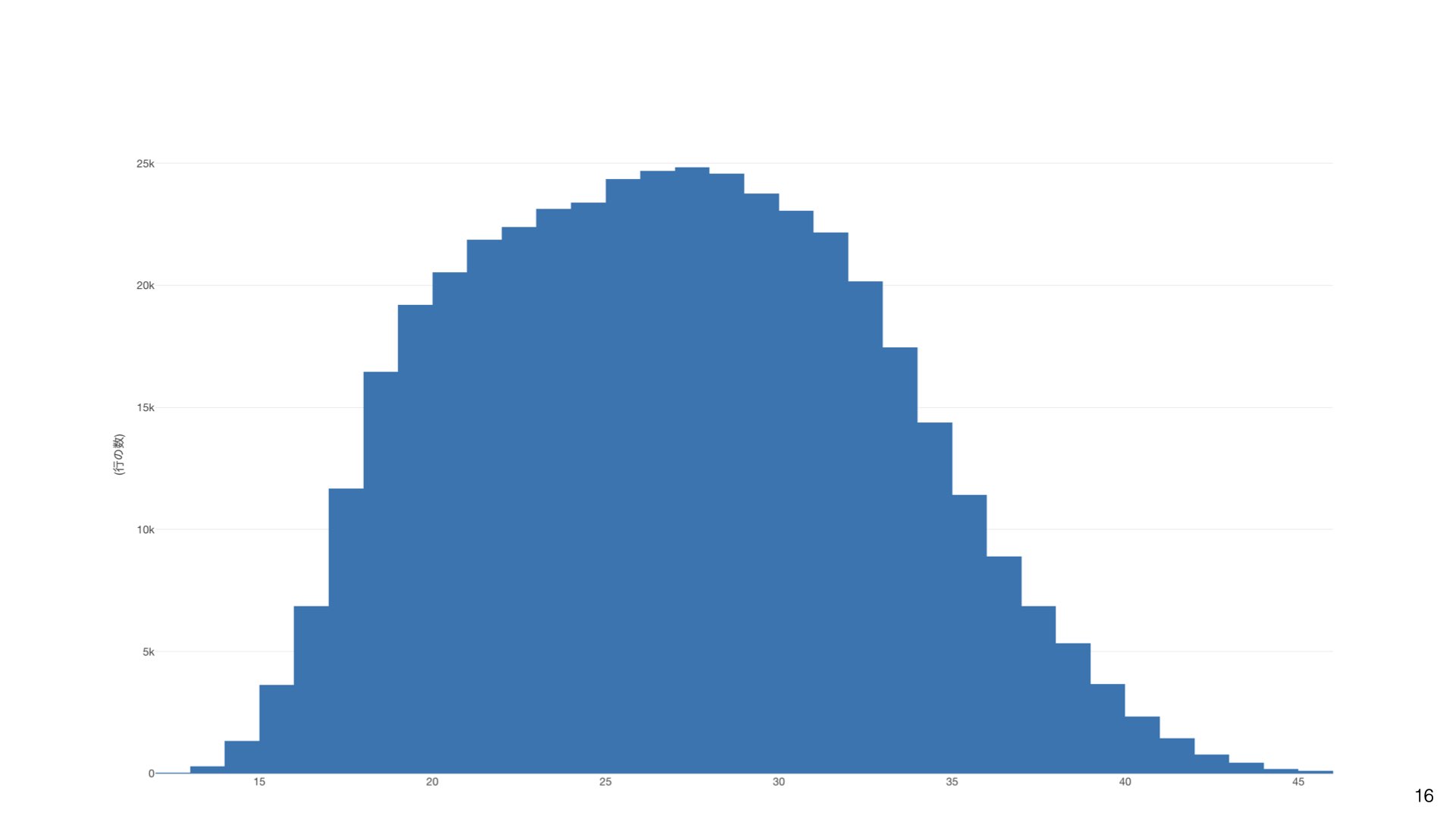
上図は正規分布のヒストグラムです。このような分布では、データが平均値を中心に左右対称に分布しています。
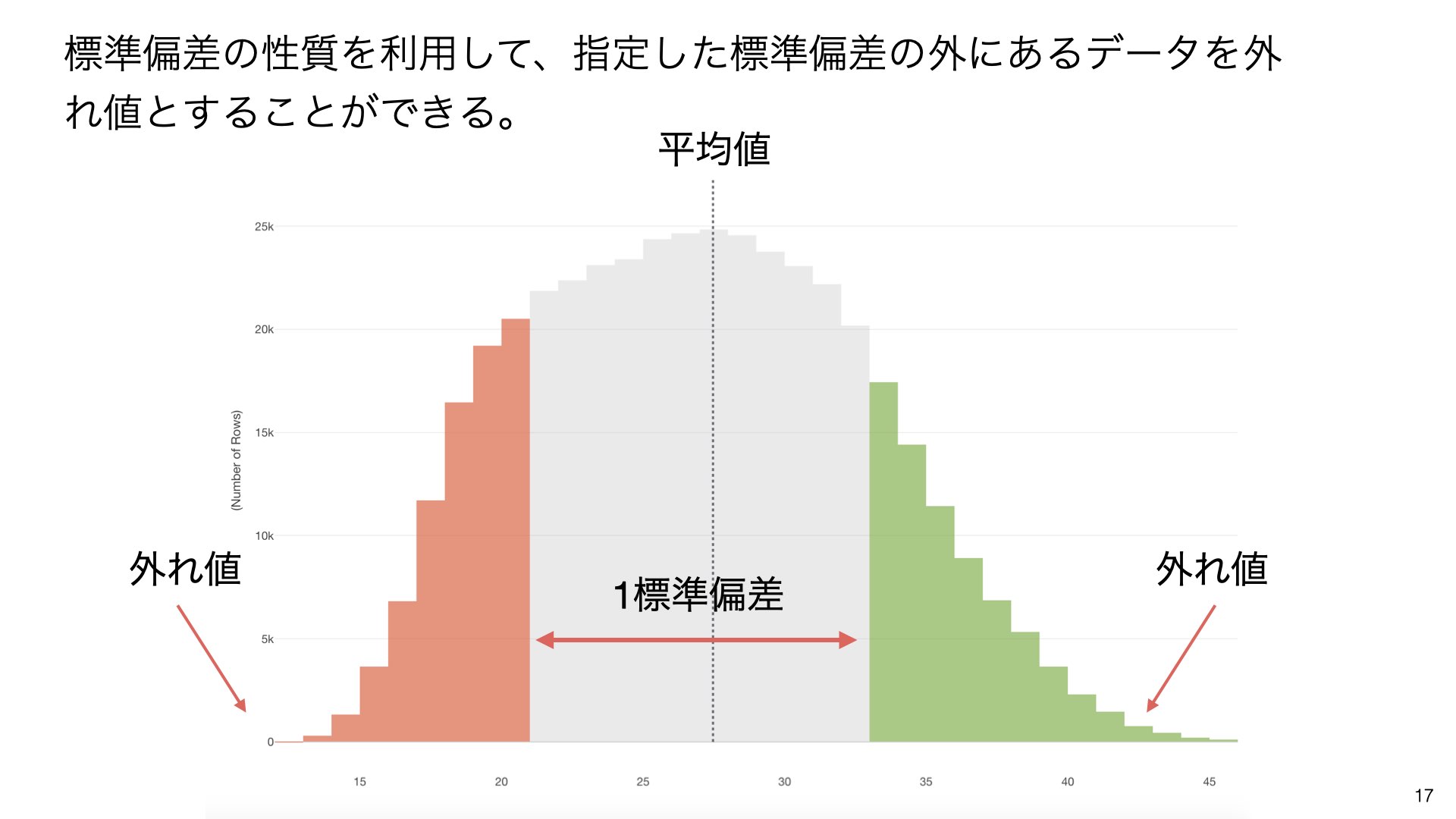
標準偏差の性質を利用して、指定した標準偏差の外にあるデータを外れ値とすることができます。上図では、平均値を中心に1標準偏差の範囲(赤い矢印)が示されています。外れ値として判定する範囲は、一般的に平均値±2標準偏差または平均値±3標準偏差の外側が使われます。
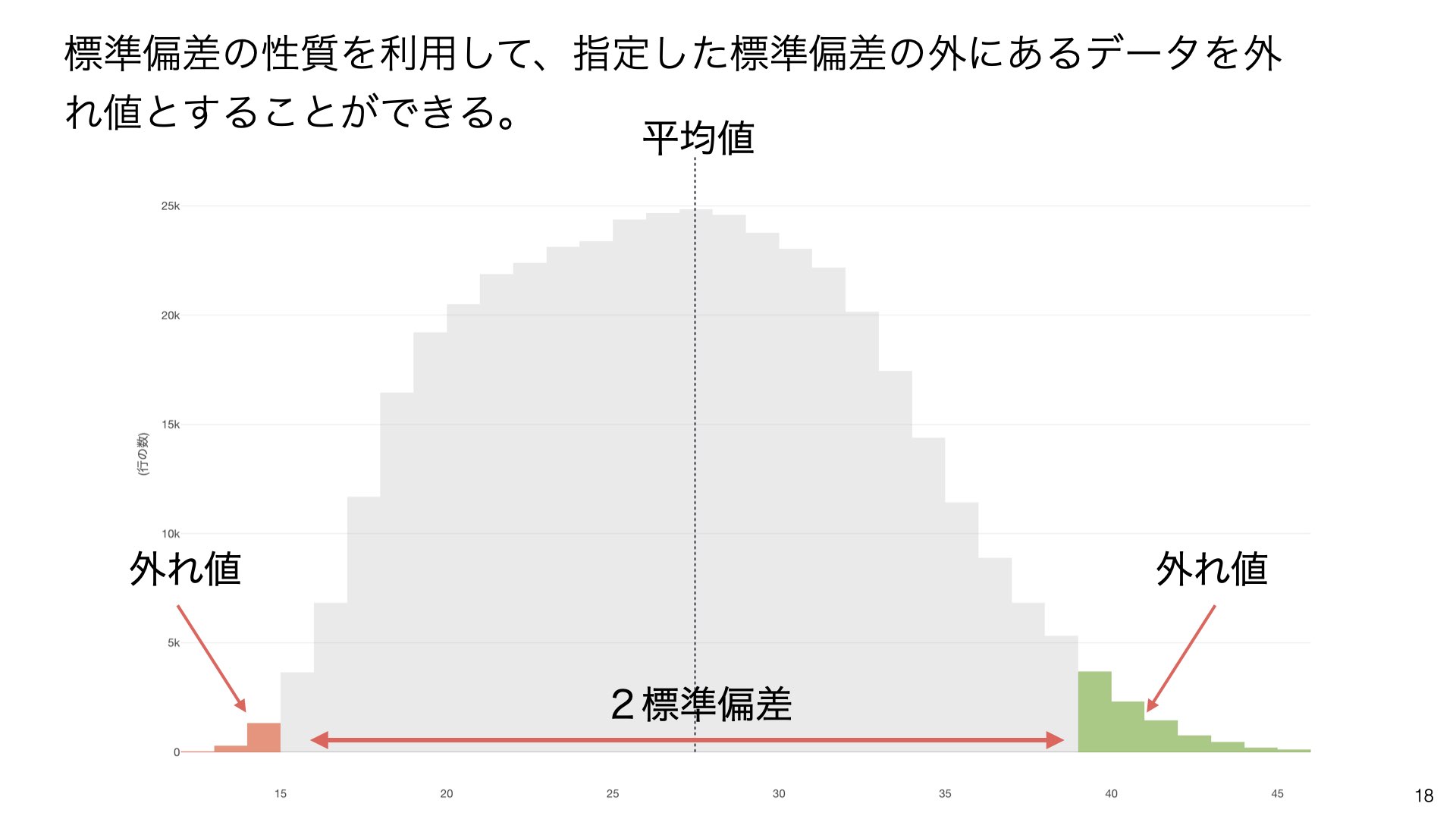
2標準偏差を使った場合、上図のように平均値から2標準偏差離れた範囲の外側(赤とオレンジの部分)にあるデータが外れ値として判定されます。
チェビシェフの不等式による理論的根拠

チェビシェフの不等式により、データのばらつきがどのようなものであれ、平均値-2標準偏差から平均値+2標準偏差の間に必ず75%以上のデータが存在することが証明されています。
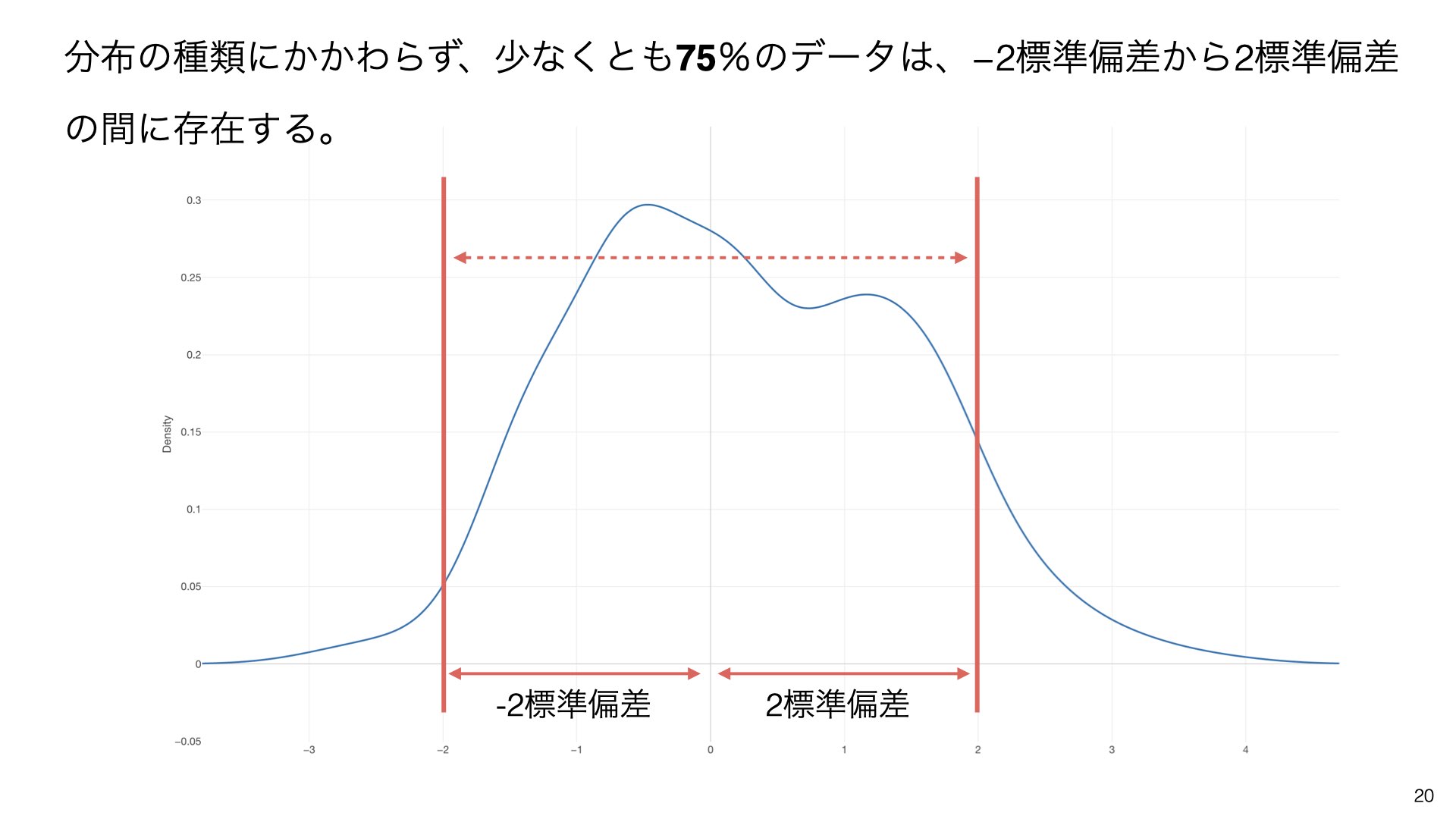
分布の種類にかかわらず、少なくとも75%のデータは、-2標準偏差から2標準偏差の間に存在します。
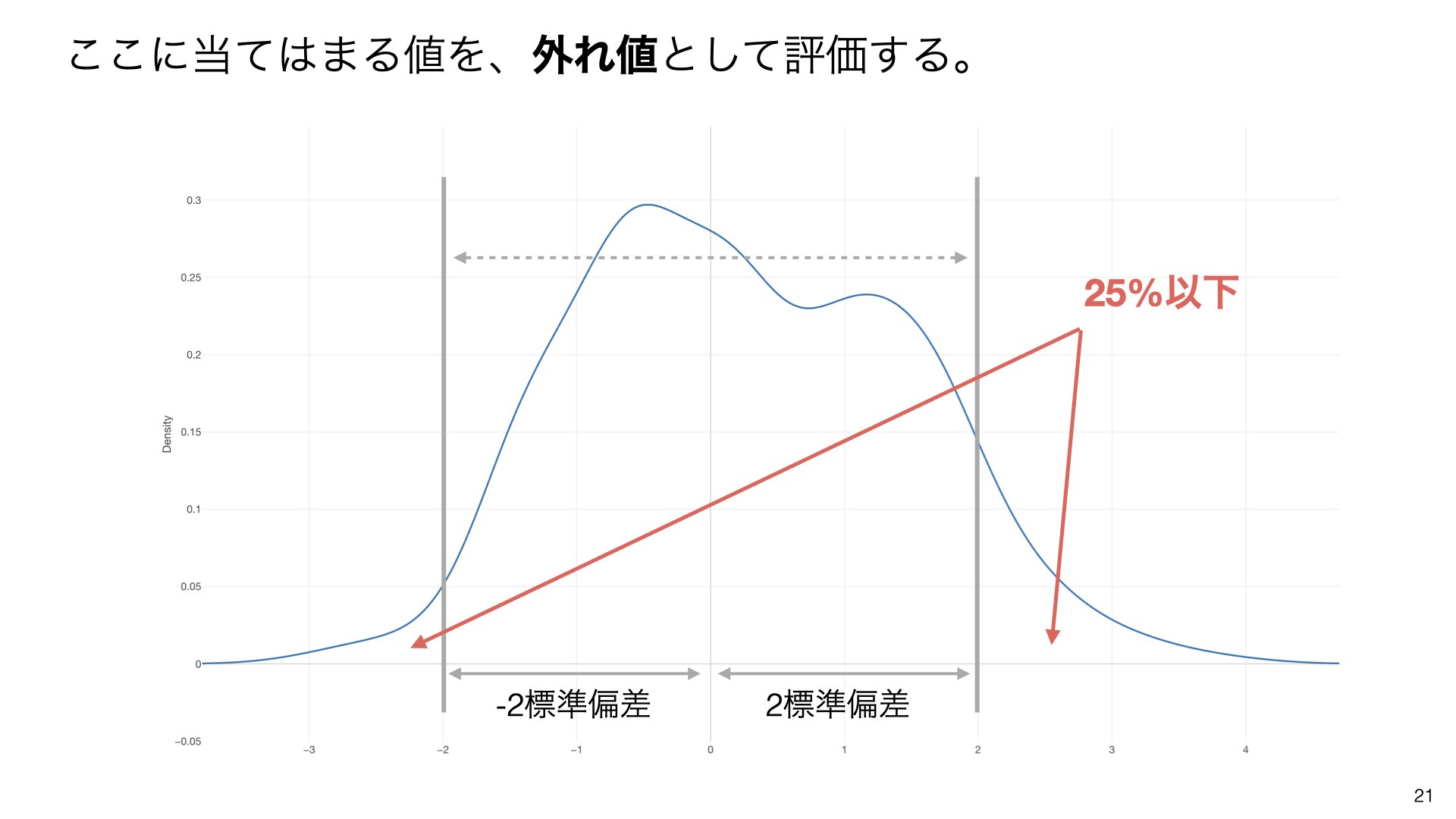
ここに当てはまる値を、外れ値として評価します。つまり、全体の25%以下の範囲にある値が外れ値の候補となります。
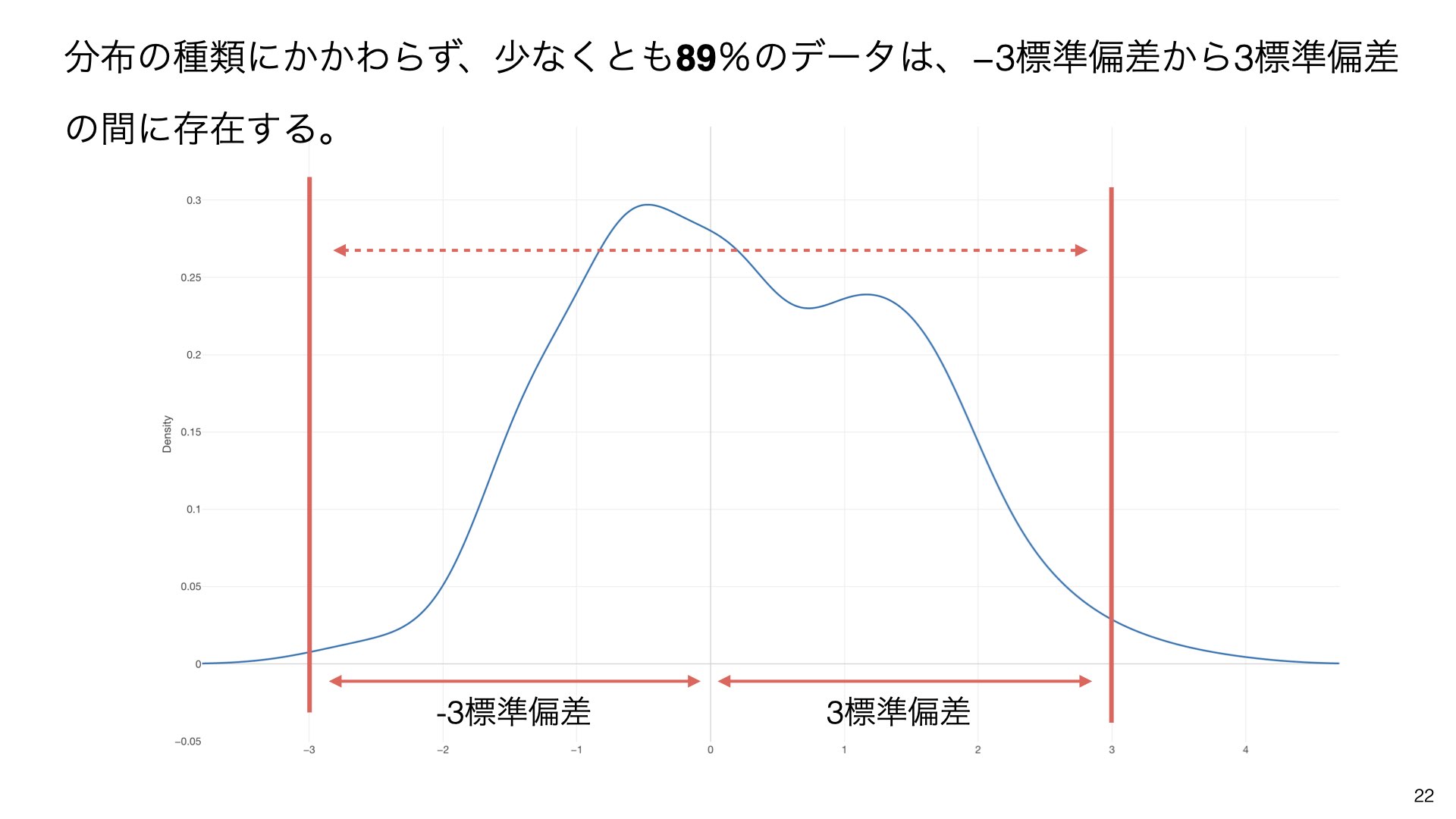
分布の種類にかかわらず、少なくとも89%のデータは、-3標準偏差から3標準偏差の間に存在します。
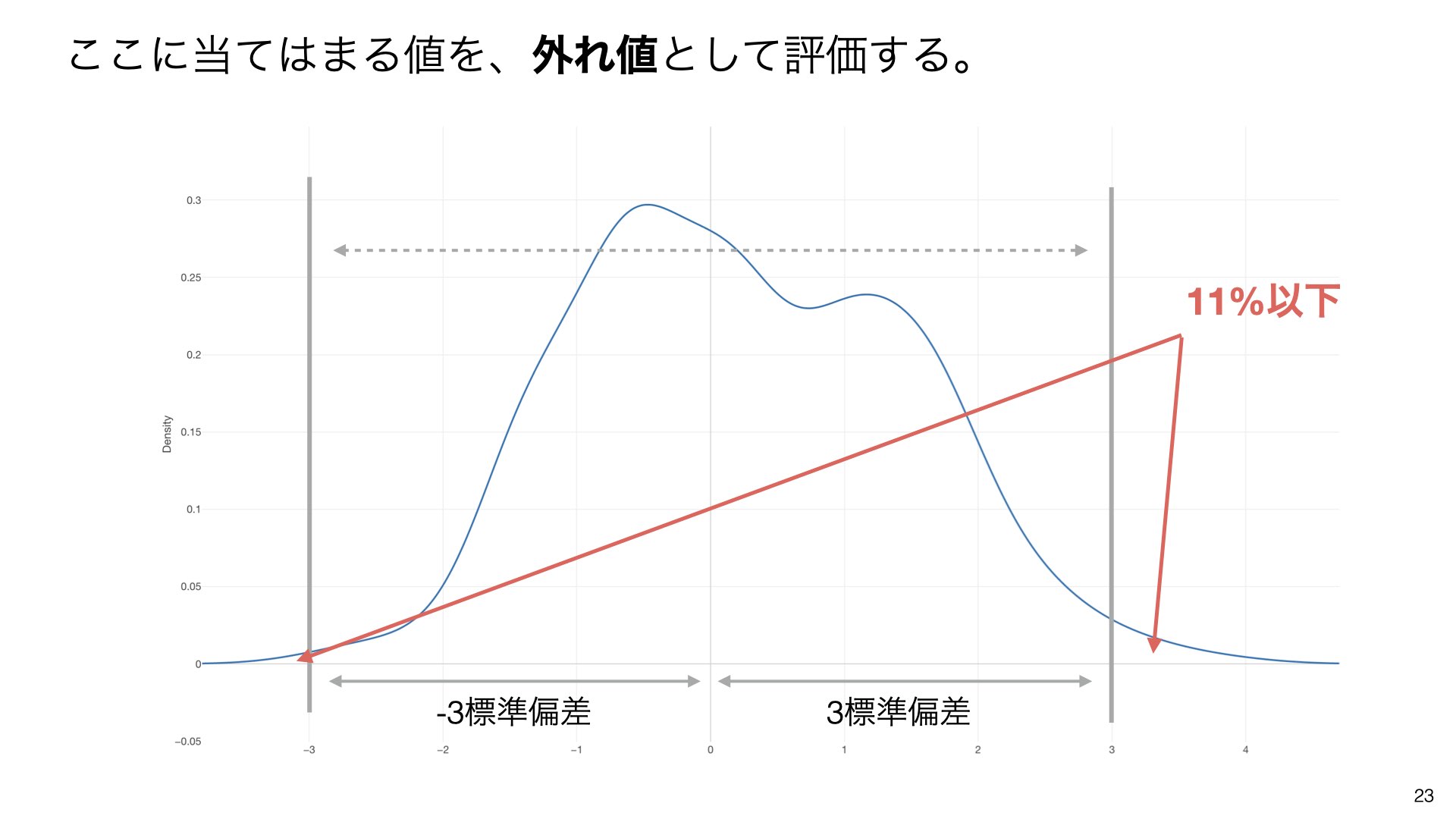
3標準偏差を基準とした場合、全体の11%以下の範囲にある値が外れ値として判定されます。
もしデータが正規分布だった場合、より正確な割合を計算できます。
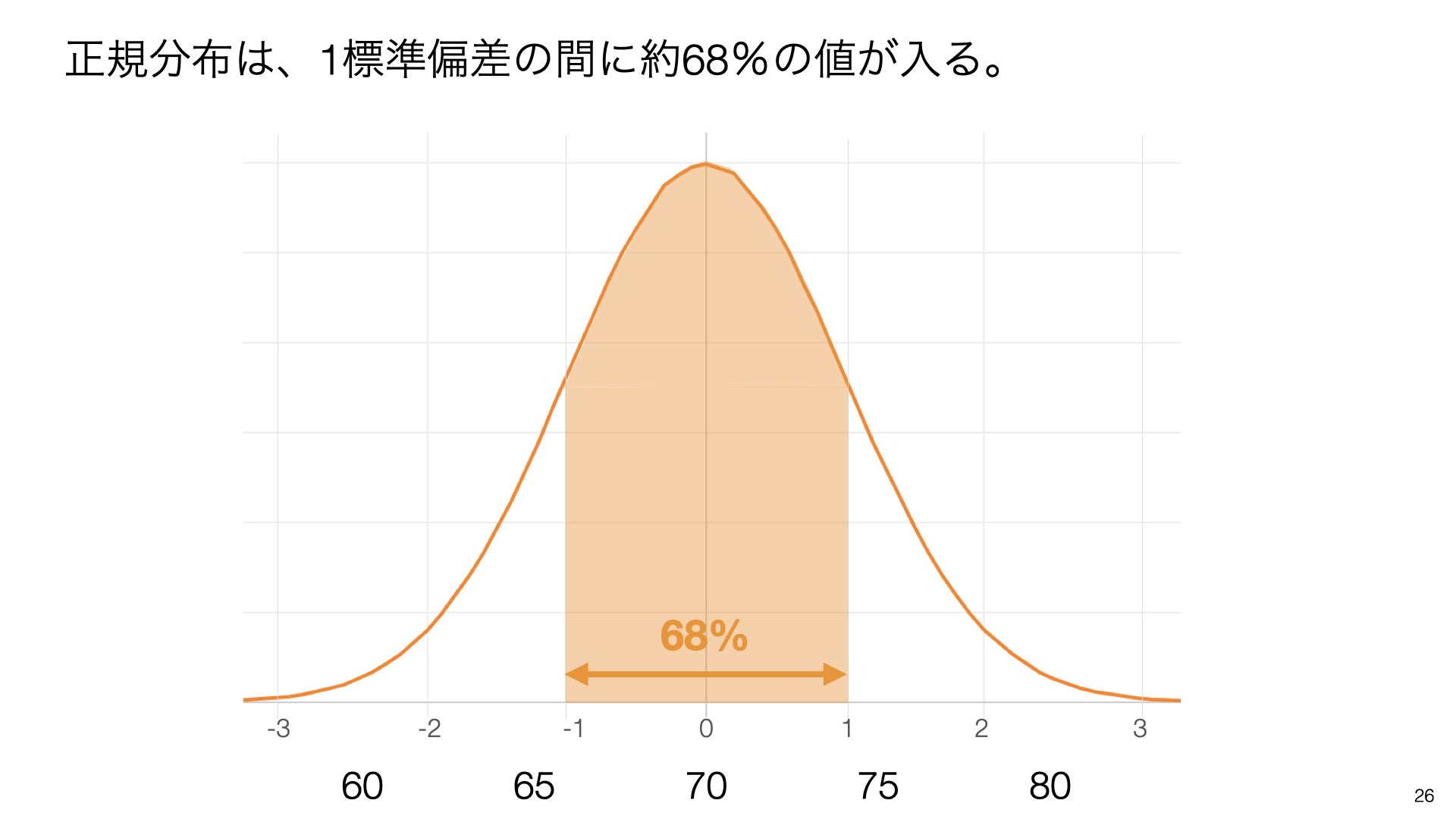
正規分布では、1標準偏差の間に約**68%**の値が入ります。
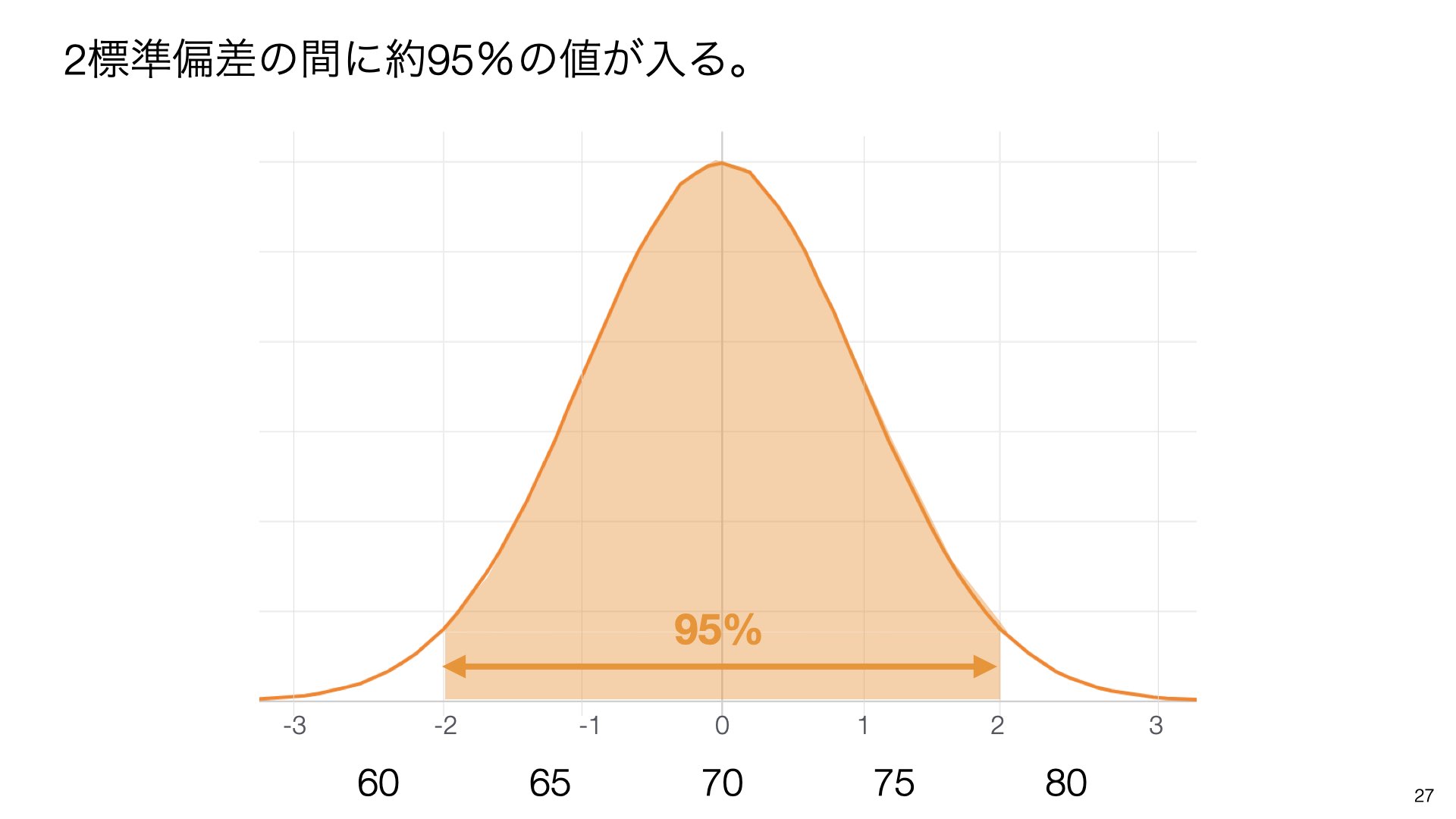
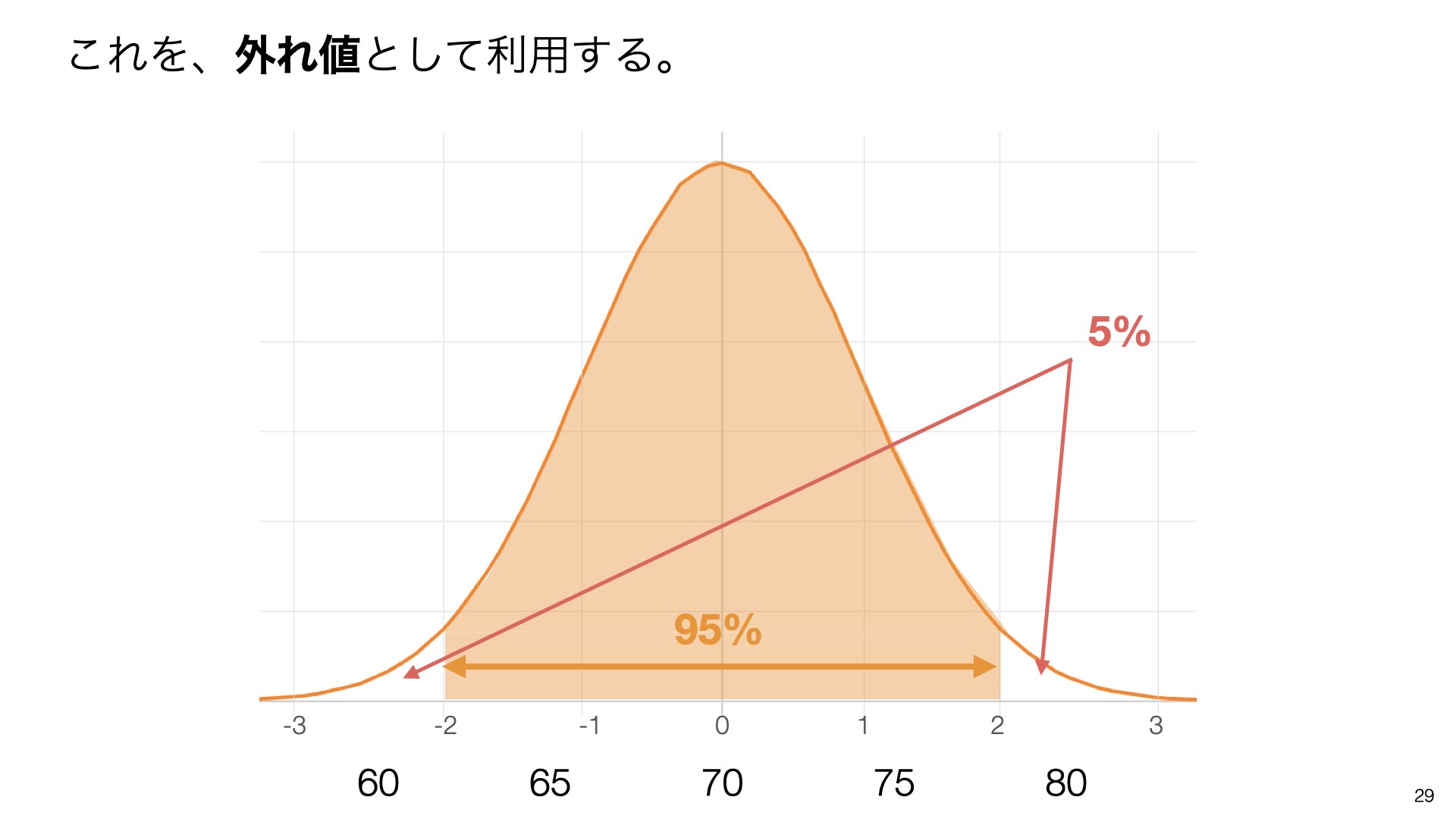
2標準偏差の間に約**95%**の値が入ります。
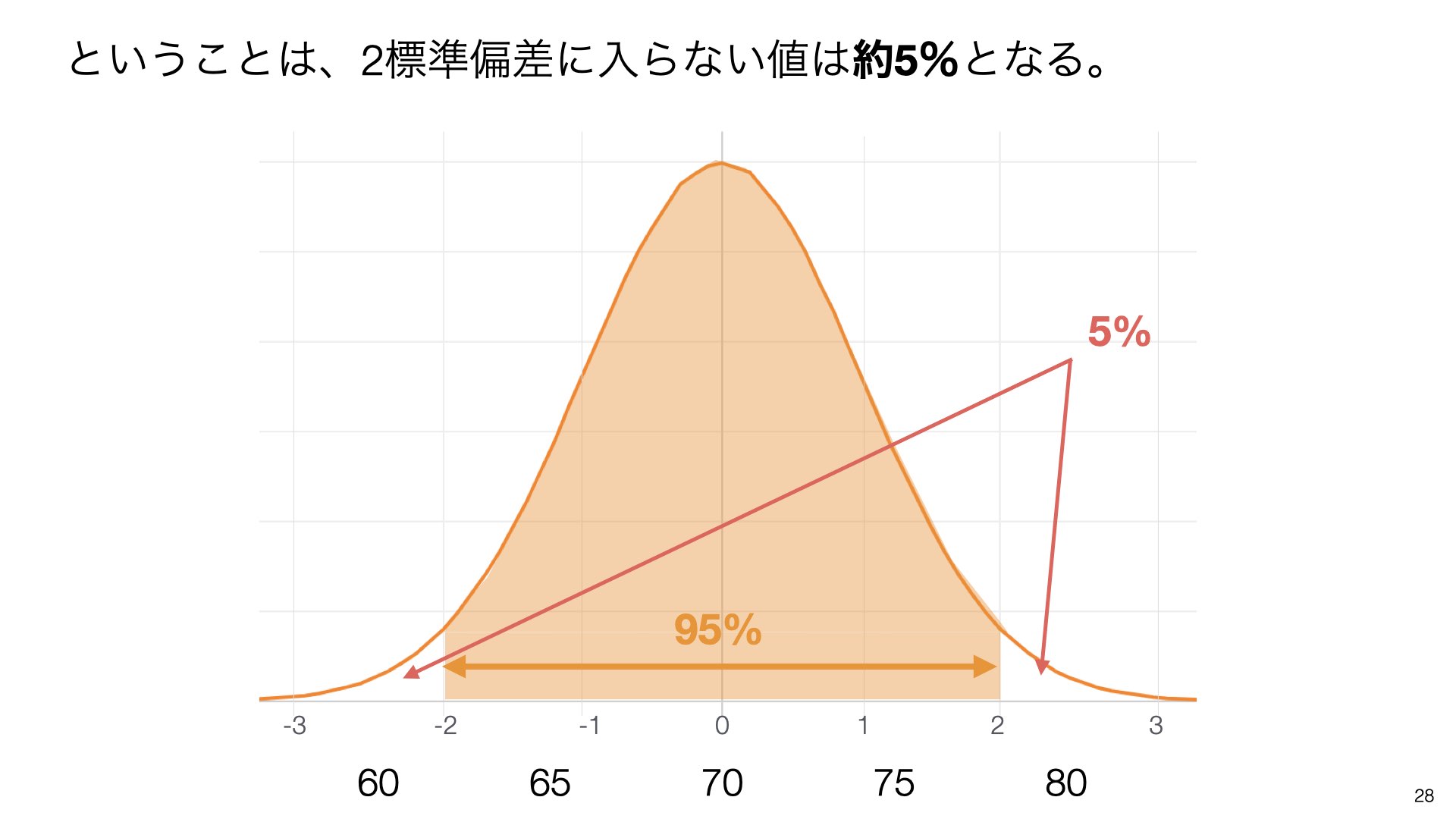
ということは、2標準偏差に入らない値は約**5%**となります。これを外れ値として利用できます。
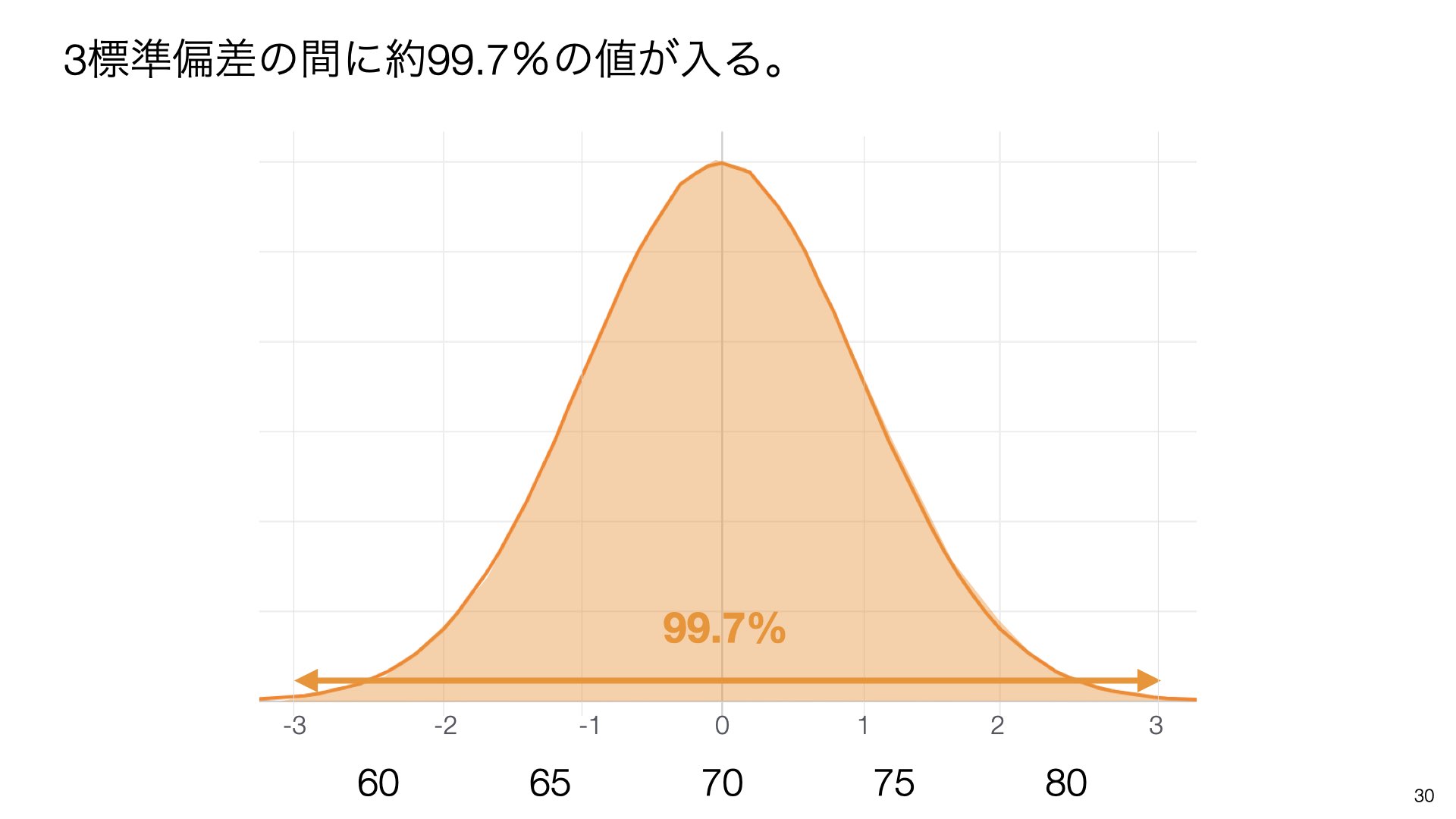
3標準偏差の間に約**99.7%**の値が入ります。
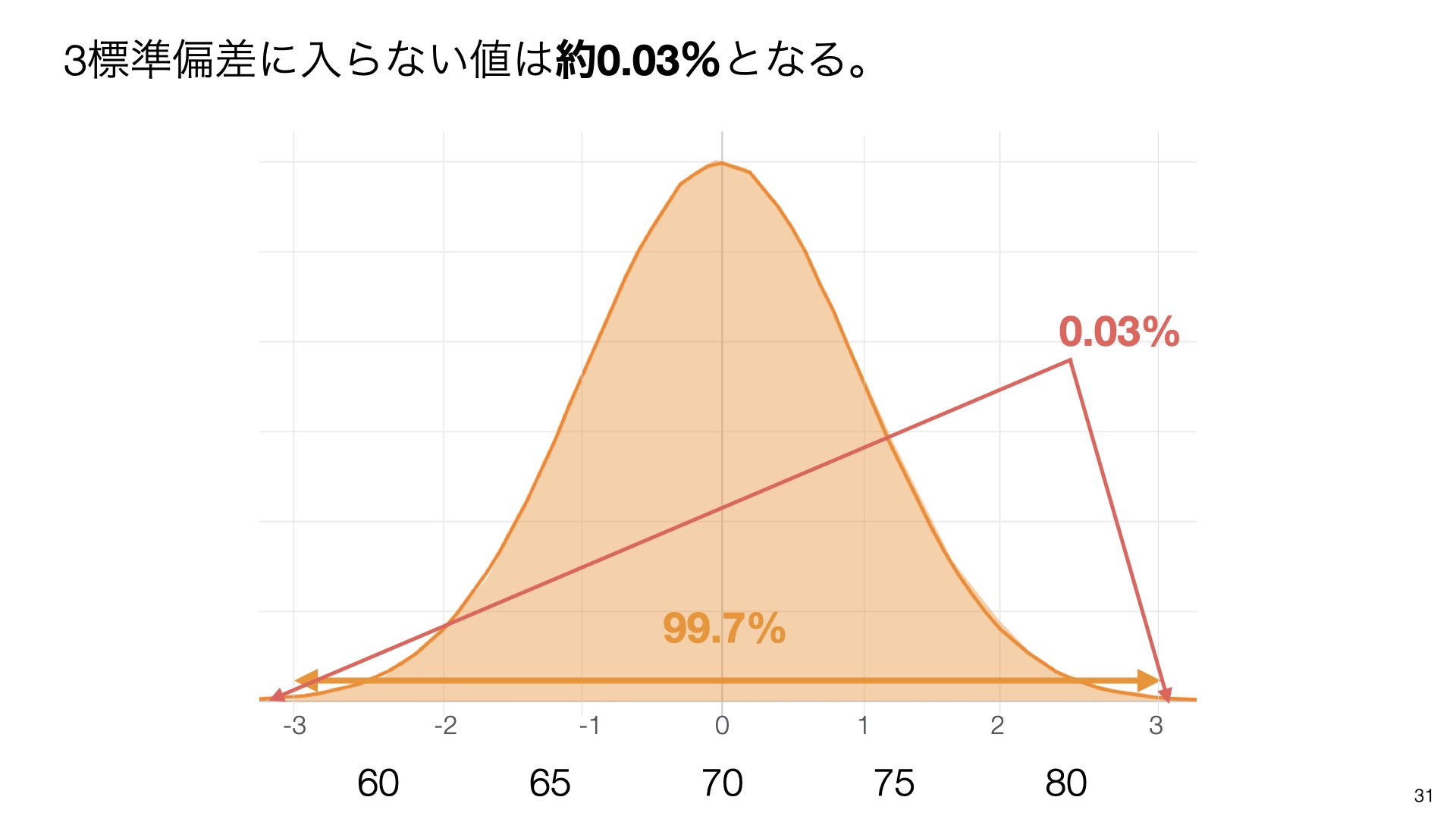
3標準偏差に入らない値は約**0.03%**となります。これを外れ値として利用できます。
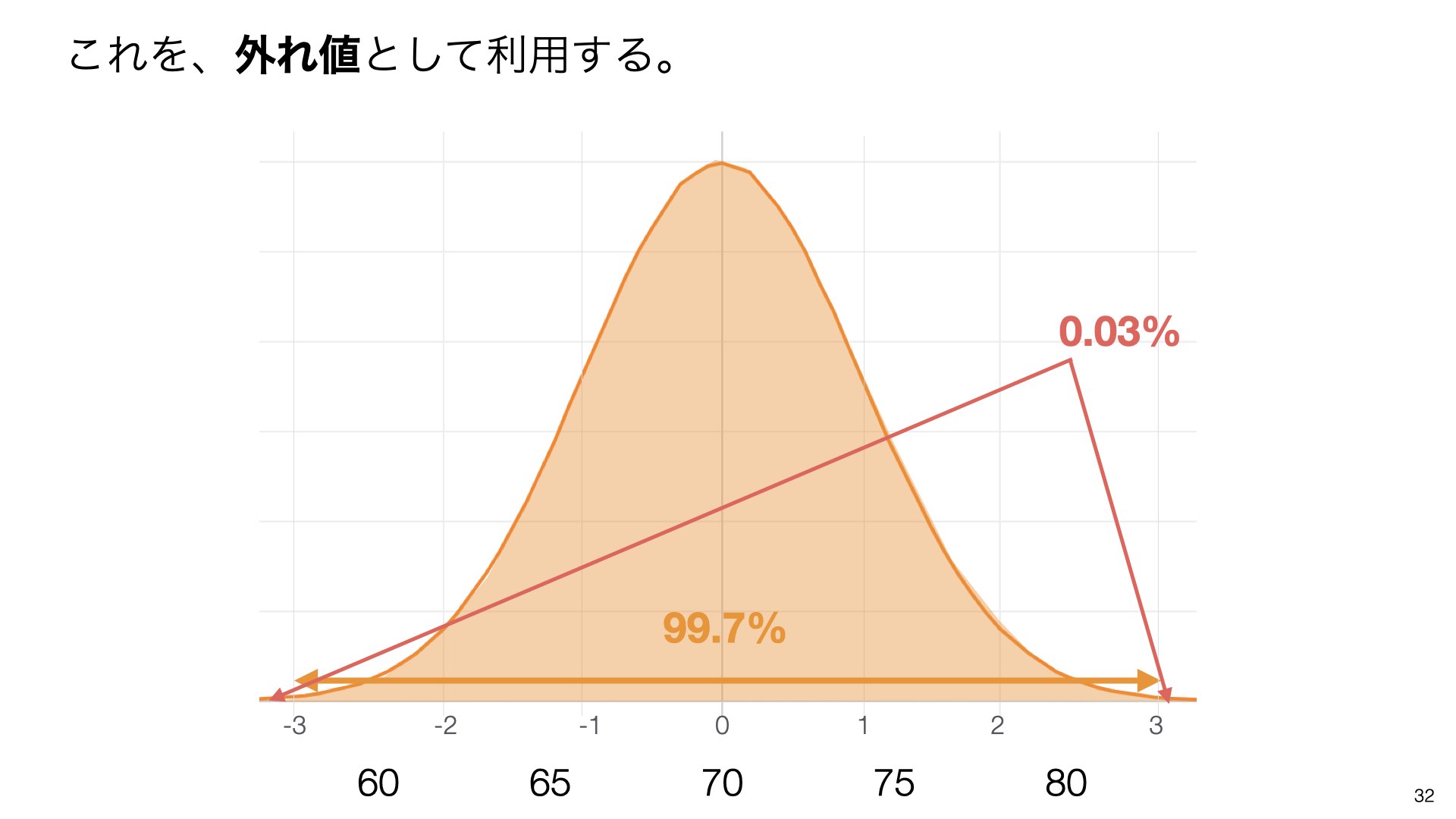
例えば、偏差値でいうと±2標準偏差ということは偏差値30から70の間ということになります。
2. パーセンタイルを使った外れ値検知
パーセンタイルは、値自体を無視して順位に着目する方法です。データを大きさ順に並べて、その値以下が全体の何パーセントを占めるかでパーセンタイルが決まります。

例えば、10人のデータで小さい方から9番目に位置する人は、90パーセンタイルになります。
一般的に、両側の10%を外れ値とする方法がよく使われます。つまり、10パーセンタイル未満と90パーセンタイル超の値を外れ値と判定します。
3. IQR(四分位範囲)を使った外れ値検知
IQRを理解するには、まず箱ひげ図を理解する必要があります。
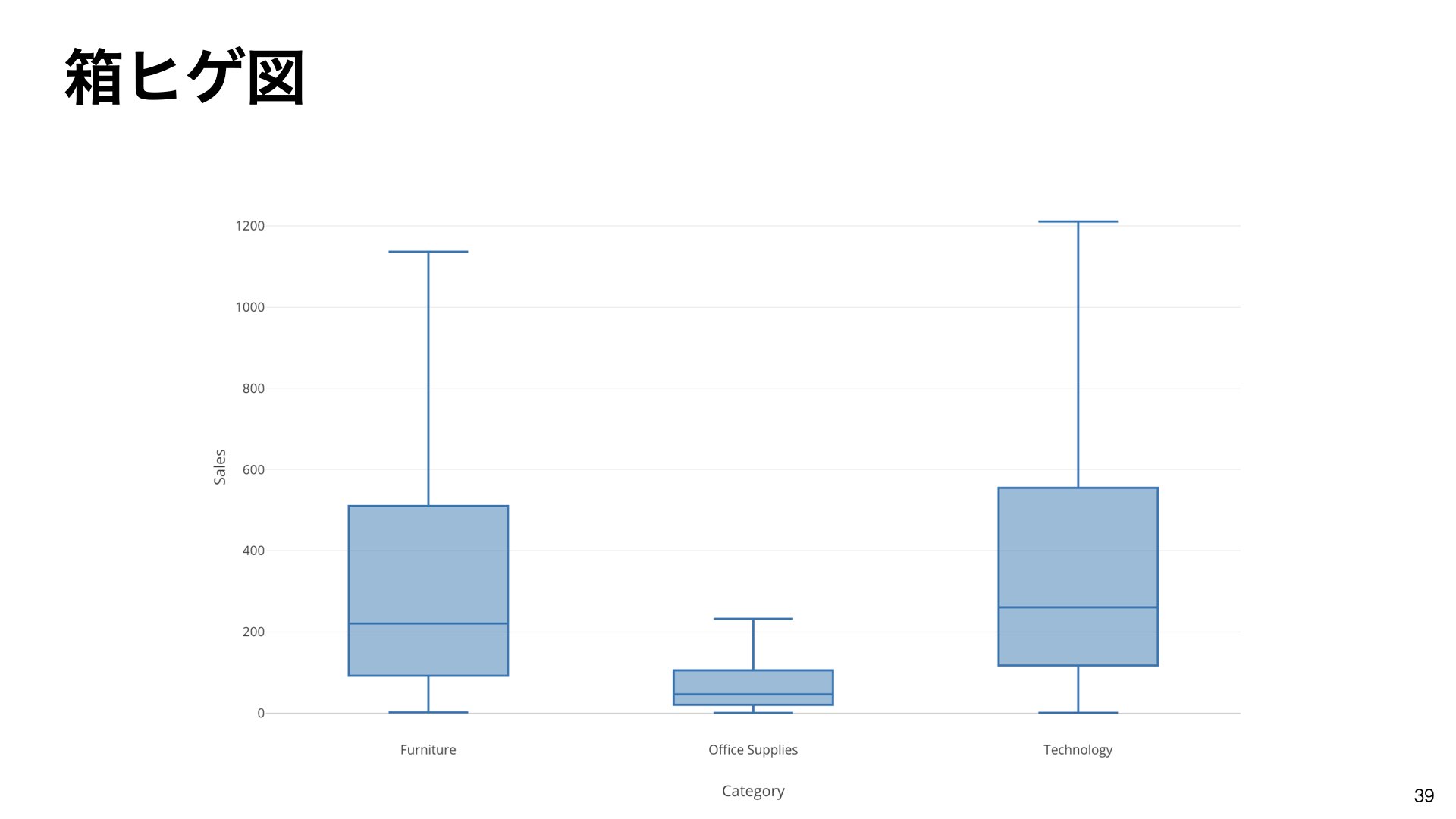
箱ひげ図は、数値データの分布をカテゴリーごとに表示します。縦軸は値の範囲を表します。
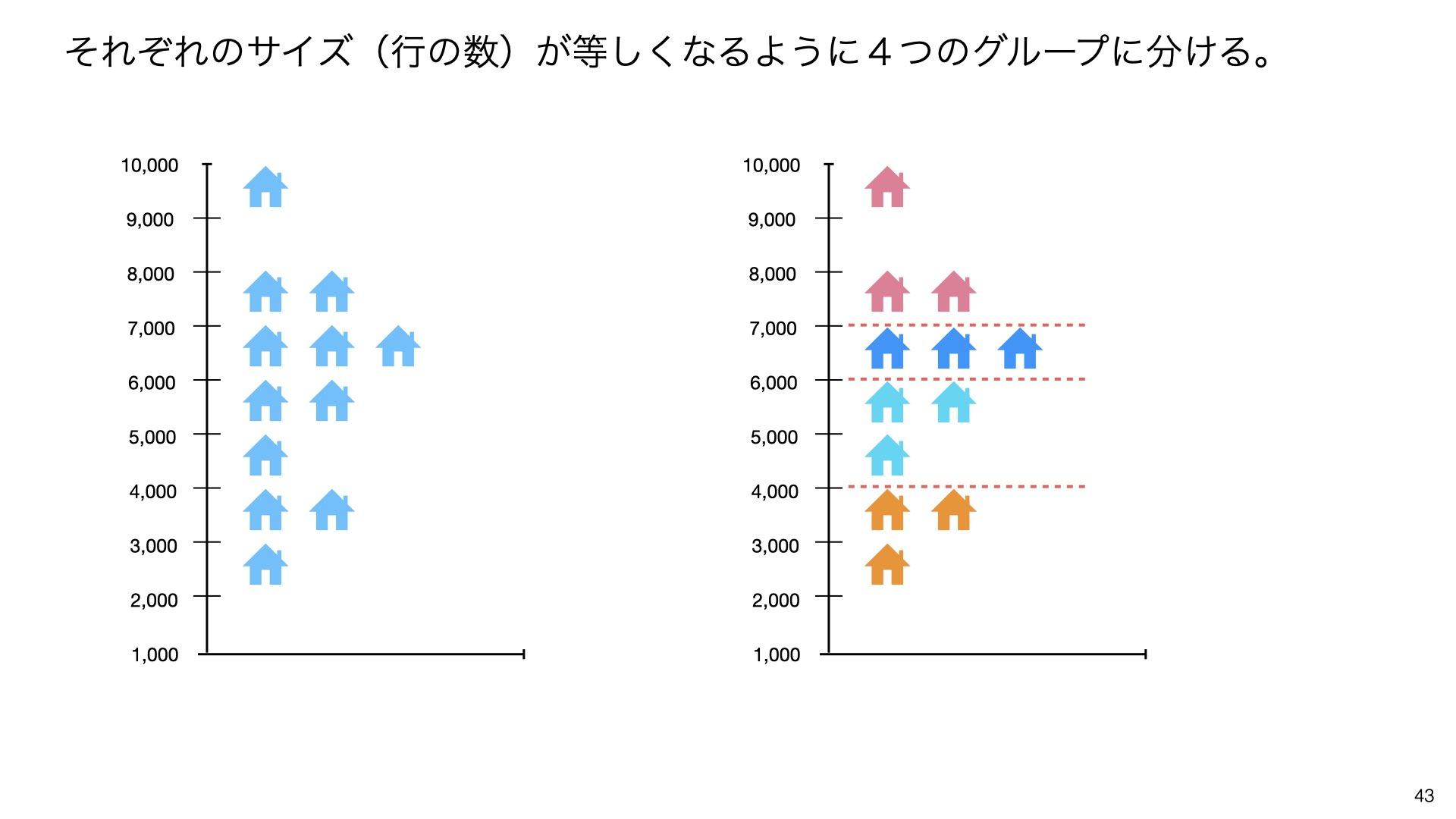
データを4つのグループに分けると、**25パーセンタイルから75パーセンタイルの範囲を四分位範囲(IQR)**と呼びます。
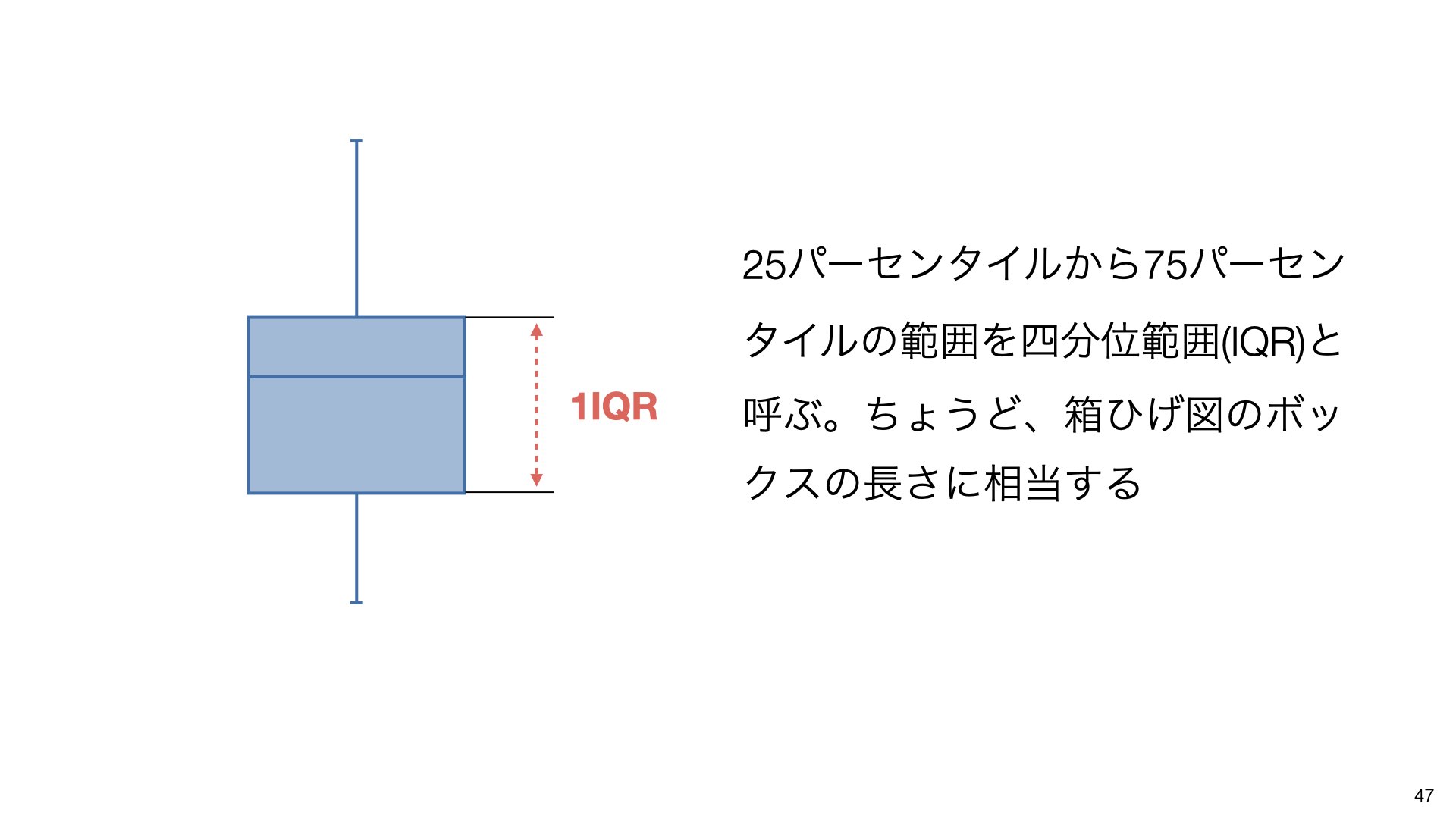
IQRの1.5倍の範囲を基準とし、箱の上端から上に1.5IQR、箱の下端から下に1.5IQRの範囲より外側の値が外れ値となります。
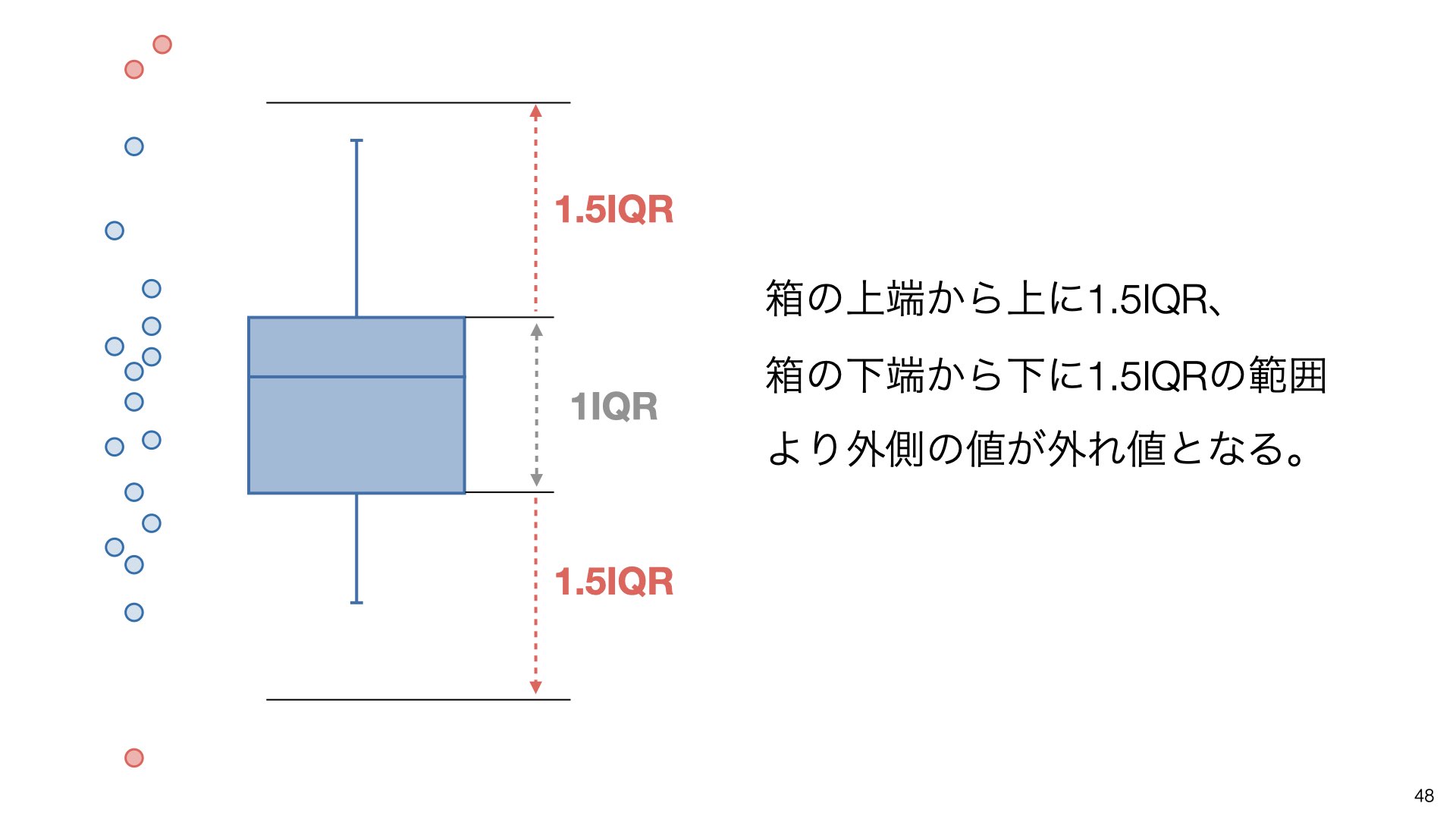
標準偏差 vs IQR

標準偏差の問題点:
分布が正規分布を前提としているが、実際のデータで正規分布であることはほとんどない
データの中に極端に異常な値があった場合、平均値や標準偏差はその値に影響を受けて、正常値とみなされる範囲が広くなり、検出すべき値を見逃してしまう可能性がある
IQRの利点:
分布の種類に限らず使うことができる(IQRの範囲自体が柔軟に分布の特徴を反映してくれる)
極端に異常な値があったとしても、IQRの計算にはそこまで影響がない
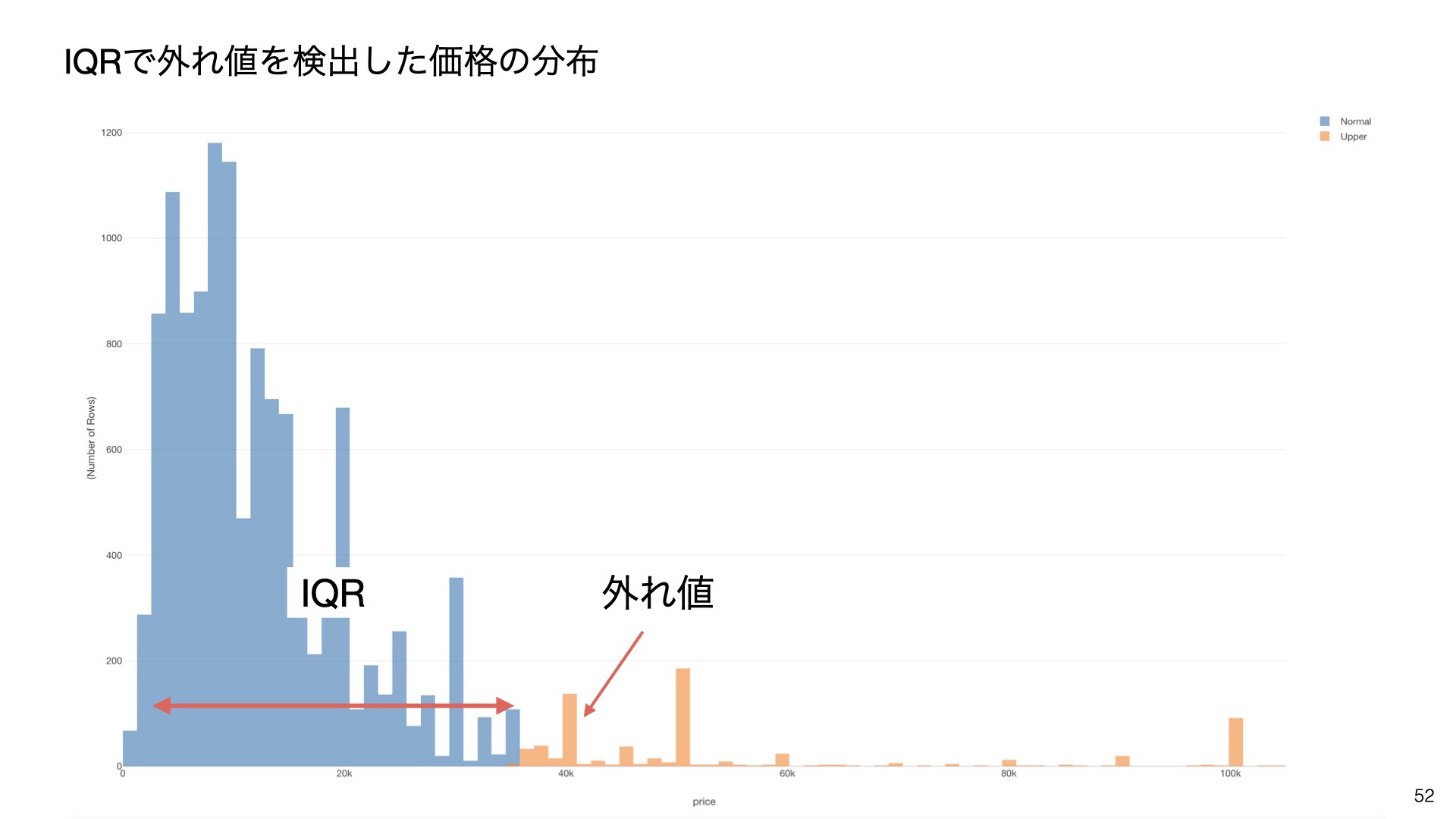
上図は、IQRで外れ値を検出した価格の分布です。IQRでは、正常だとみなされる範囲が0円から3万5千円と標準偏差に比べて範囲が狭く、標準偏差に比べて上手く外れ値を検出できています。
実際のフィルタを使った外れ値除去
実際の分析ツールでは、以下の方法で外れ値を取り除くことができます:
1. ステップのフィルタで外れ値を取り除く
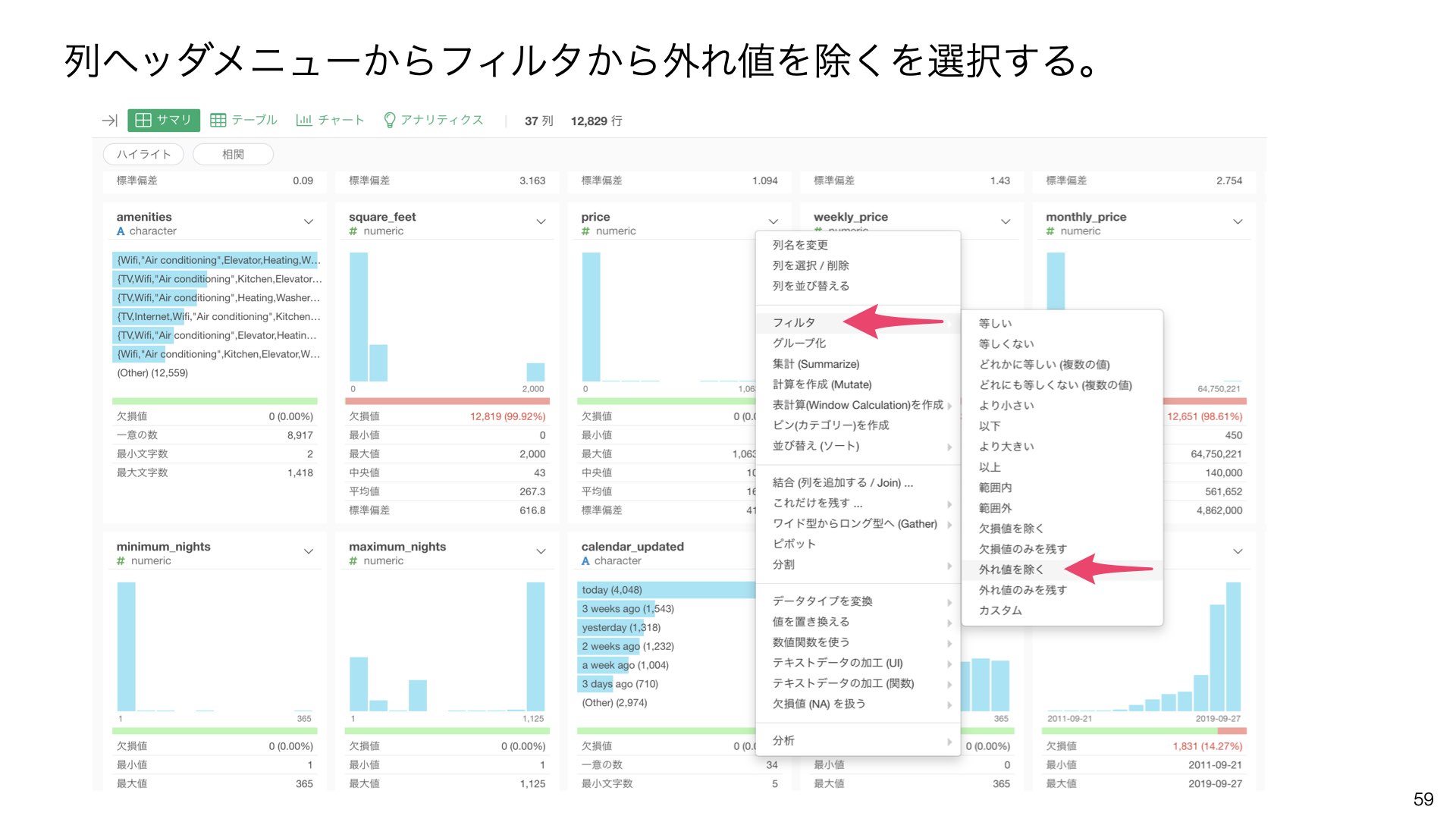
列ヘッダメニューから「フィルタ」→「外れ値を除く」を選択します。
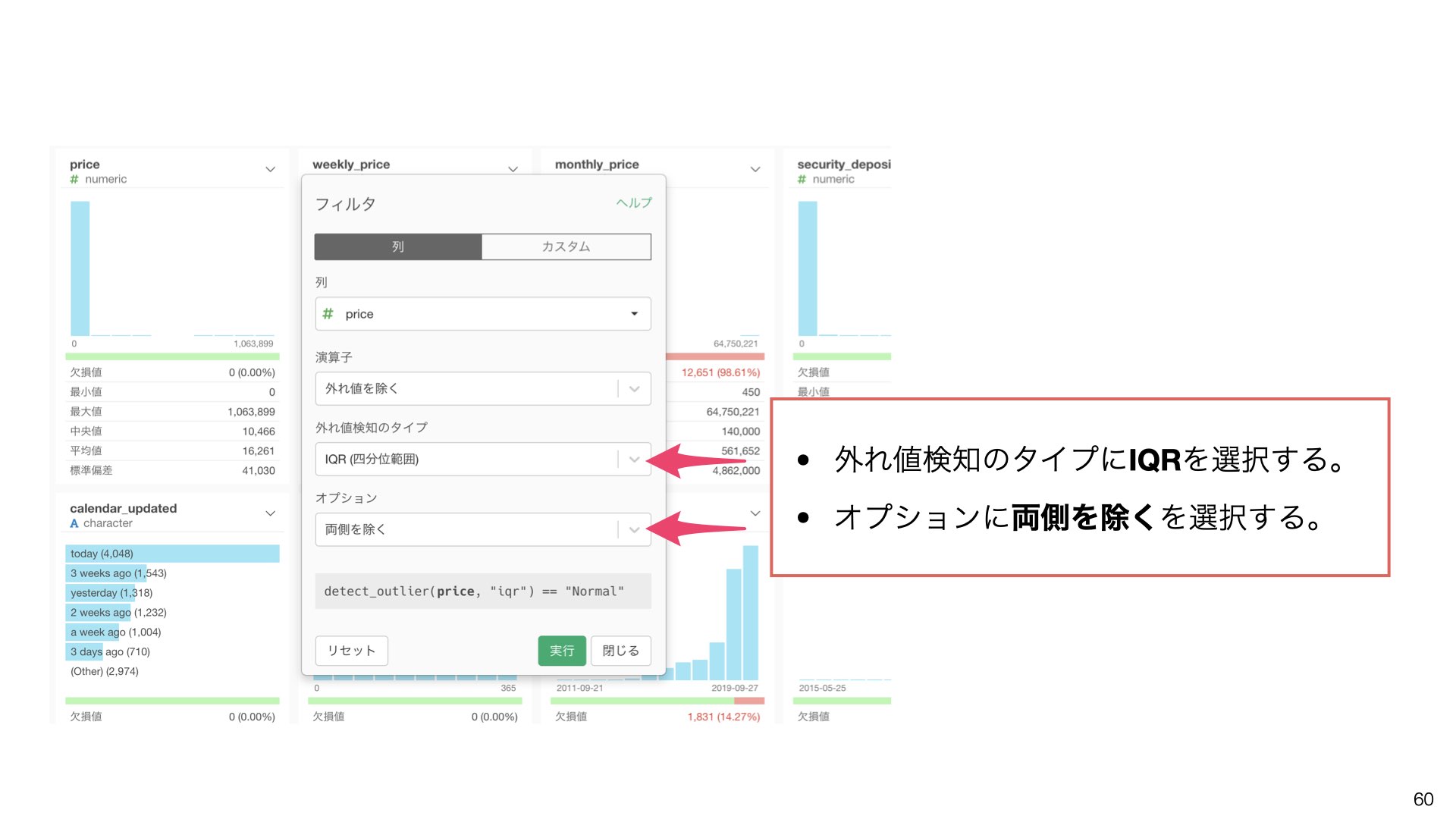
外れ値検知のタイプにIQRを選択する
オプションに両側を除くを選択する
これにより、価格の外れ値を取り除くことができ、12,085行のデータから外れ値を除外した12,085行のクリーンなデータが得られます。
2. チャート(アナリティクス)内フィルタで外れ値を取り除く
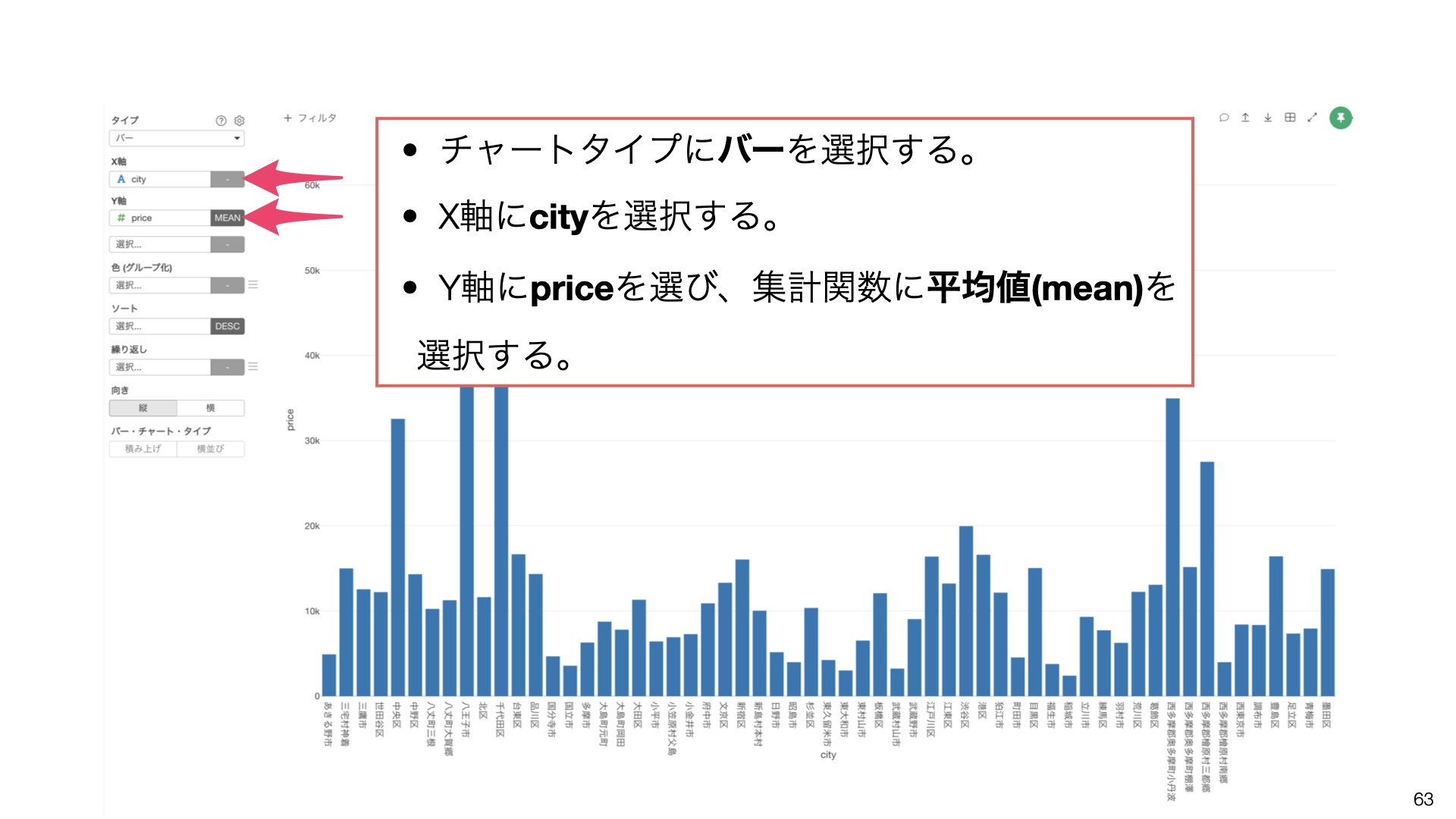
チャートを作成する際に:
チャートタイプにバーを選択
X軸にcityを選択
Y軸にpriceを選び、集計関数に**平均値(mean)**を選択
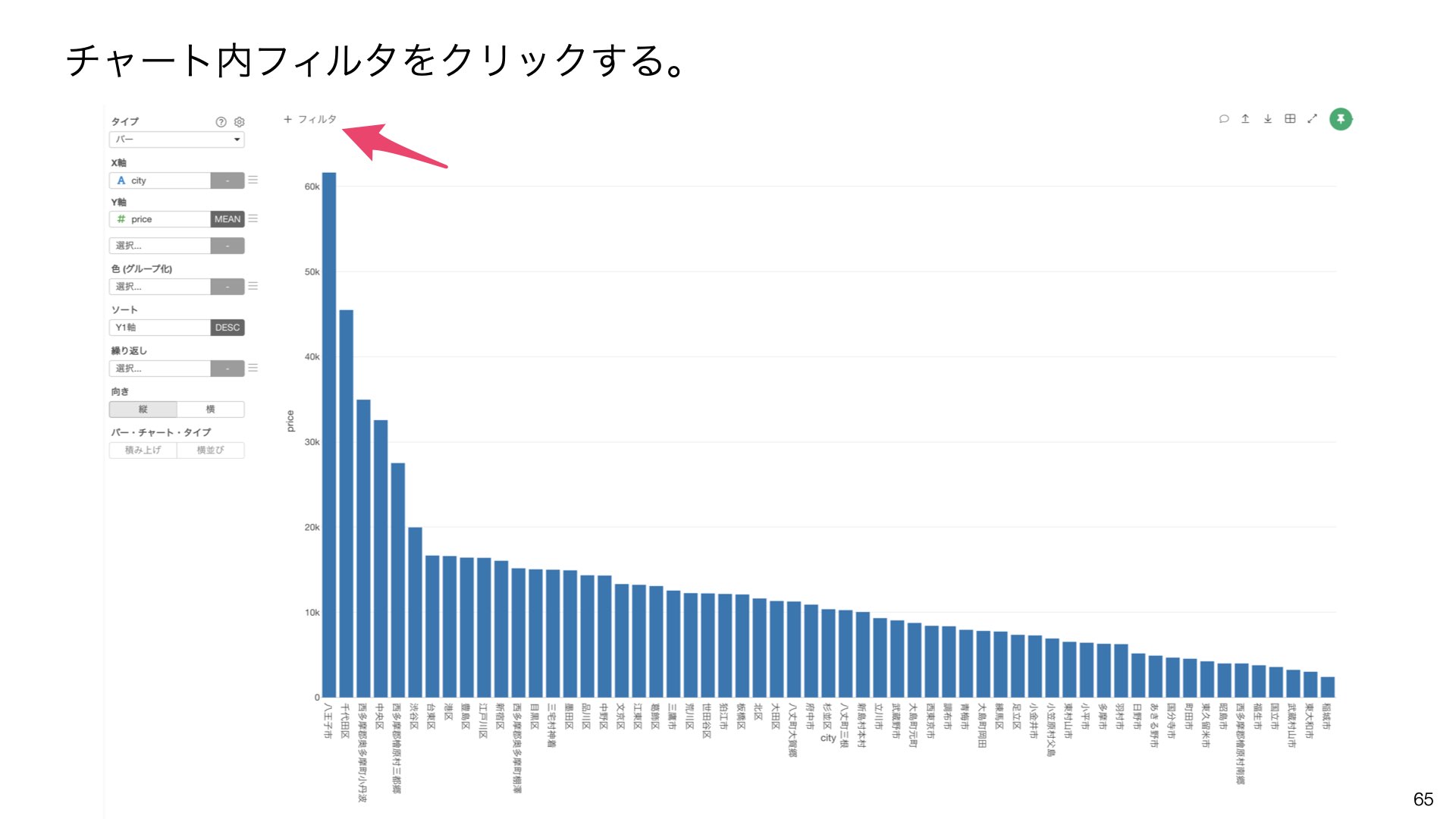
チャート内フィルタをクリックして、以下を設定します:
演算子に外れ値を除くを選択
外れ値検知のタイプにIQRを選択
オプションに両側を除くを選択
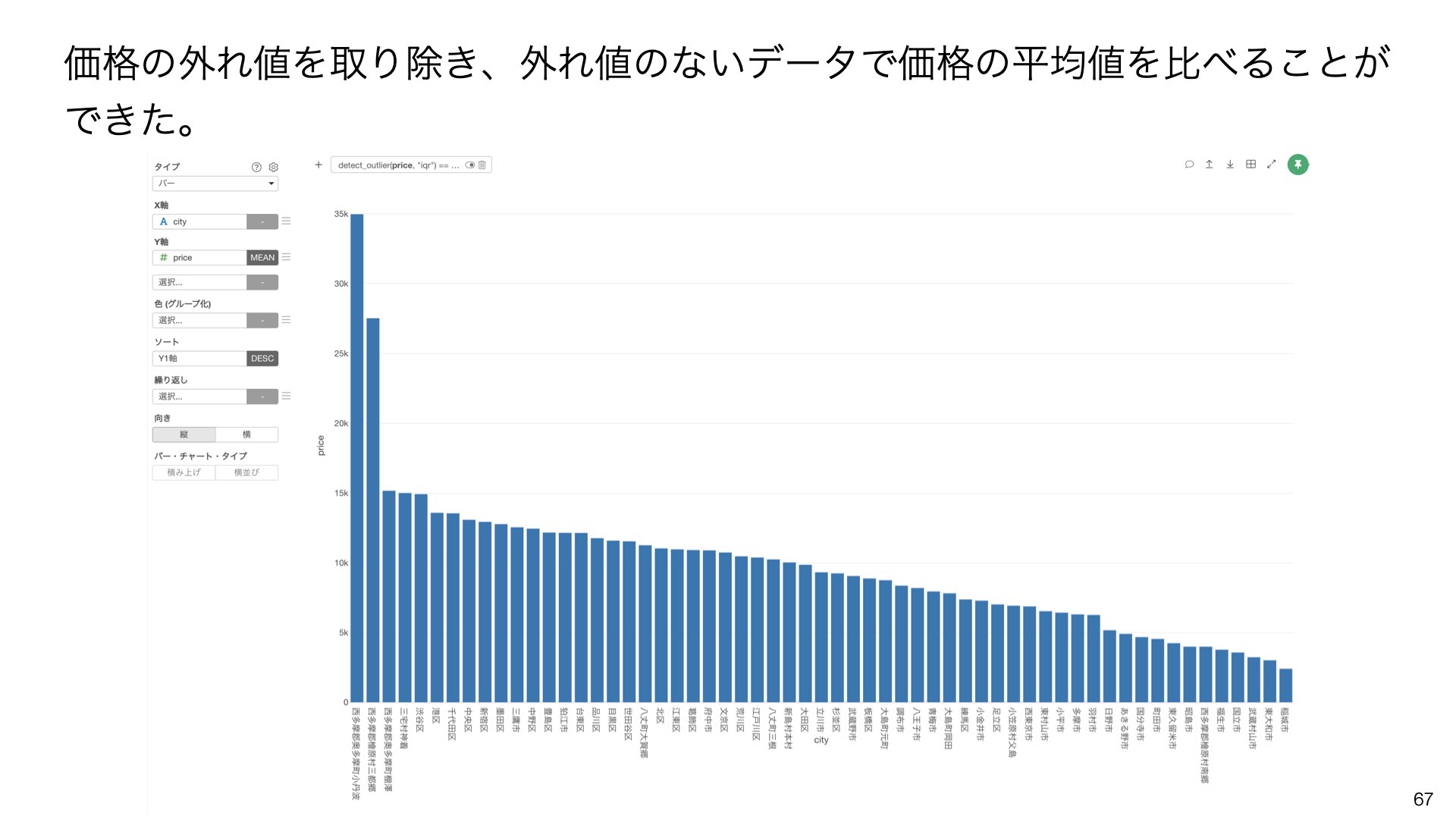
これにより、価格の外れ値を取り除き、外れ値のないデータで価格の平均値を比べることができます。
まとめ
外れ値検知とは、データの標準的な分布から大きく離れた値を見つけ出し、分析の精度を向上させる重要な手法です。