マーケティング領域におけるExploratoryの活用 Part 4 - 線形回帰
このノートは、マーケティング領域でExploratoryを効率的に使い始めることができるように作られた「マーケティング領域におけるExploratoryの活用」の第4弾、「線形回帰」編です。
データをインポートする
今回はサンプルデータとして「Airbnbのベルギーの宿泊施設」のデータを使用します。このデータは1行が1物件になっており、それぞれの物件に関する価格や広さなどの情報が列として入っています。
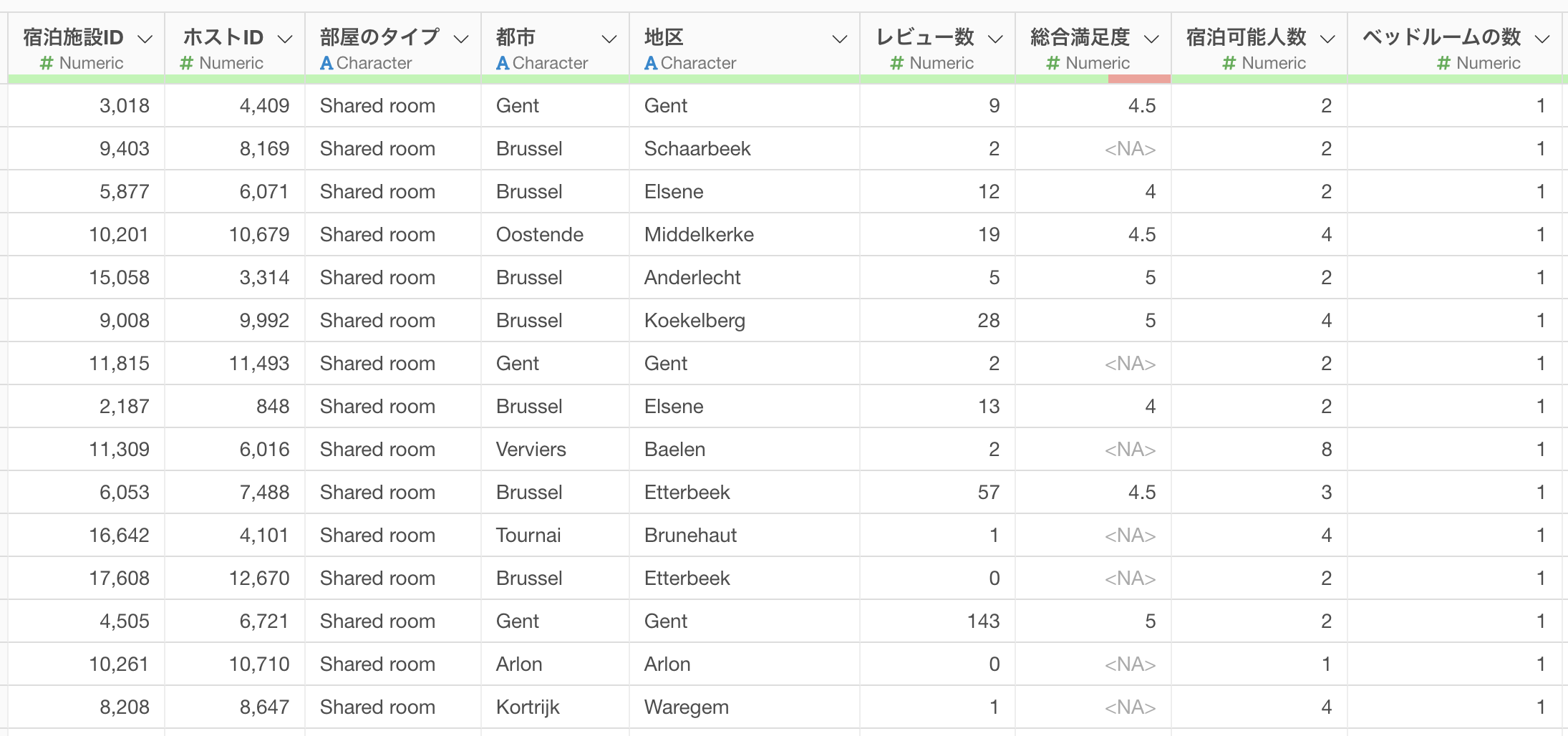
データはこちらのページからダウンロードできます。Macをお使いの方は「CSV-UTF8」を、Windowsをお使いの方は「CSV - Shift-JIS」をダウンロードしてください。
Airbnbのデータをダウンロードできたら、ダウンロードしたフォルダを開き、「Airbnbのベルギーの宿泊施設データ.csv」をExploratoryの画面にドラッグ&ドロップします。
インポートダイアログが表示されました。インポートダイアログの左側にある項目から、インポート時の設定を行うことが可能ですが、今回は設定は不要なため「インポート」ボタンをクリックします。
任意のデータフレーム名を指定して、「作成」ボタンをクリックします。
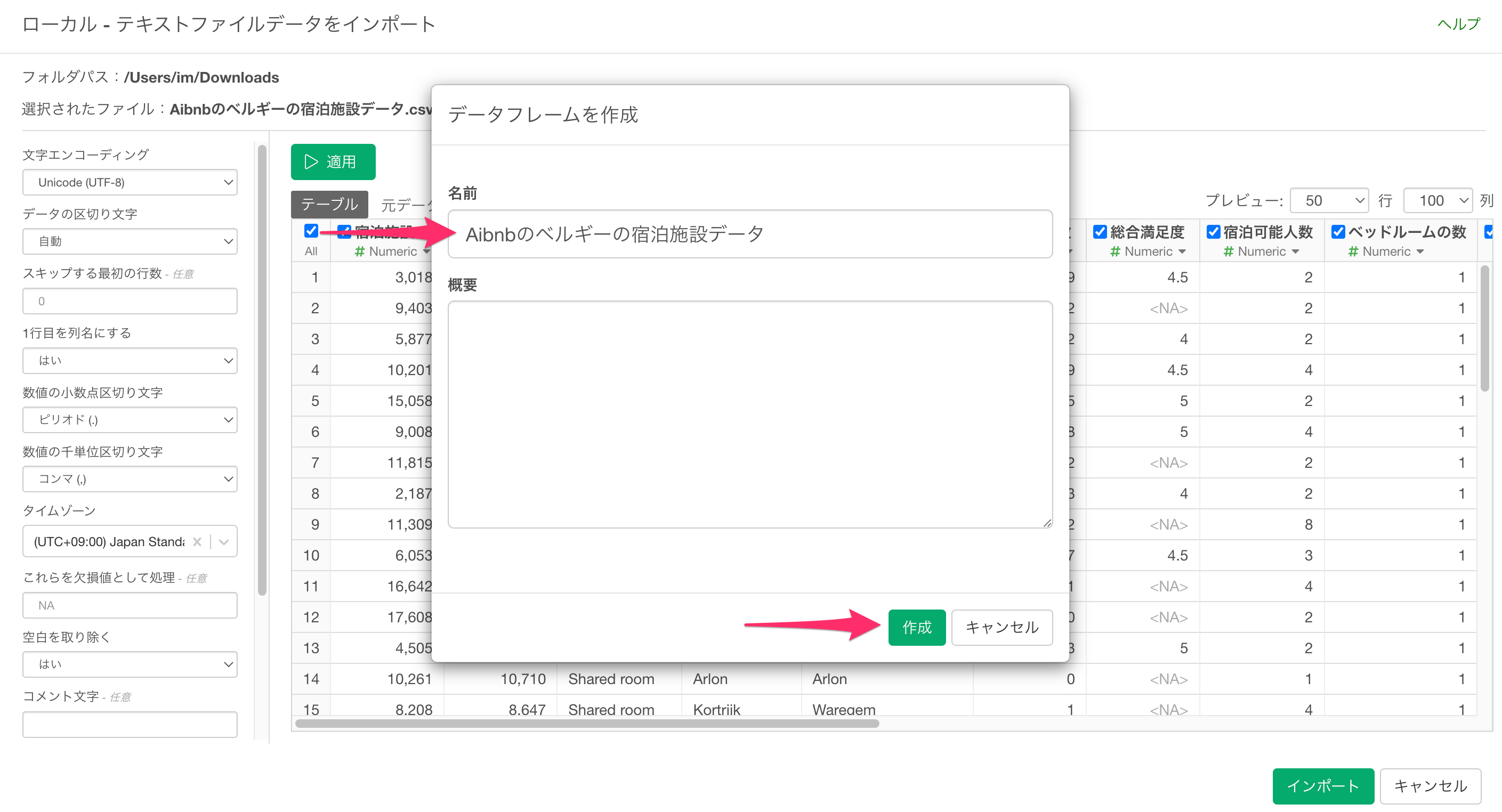
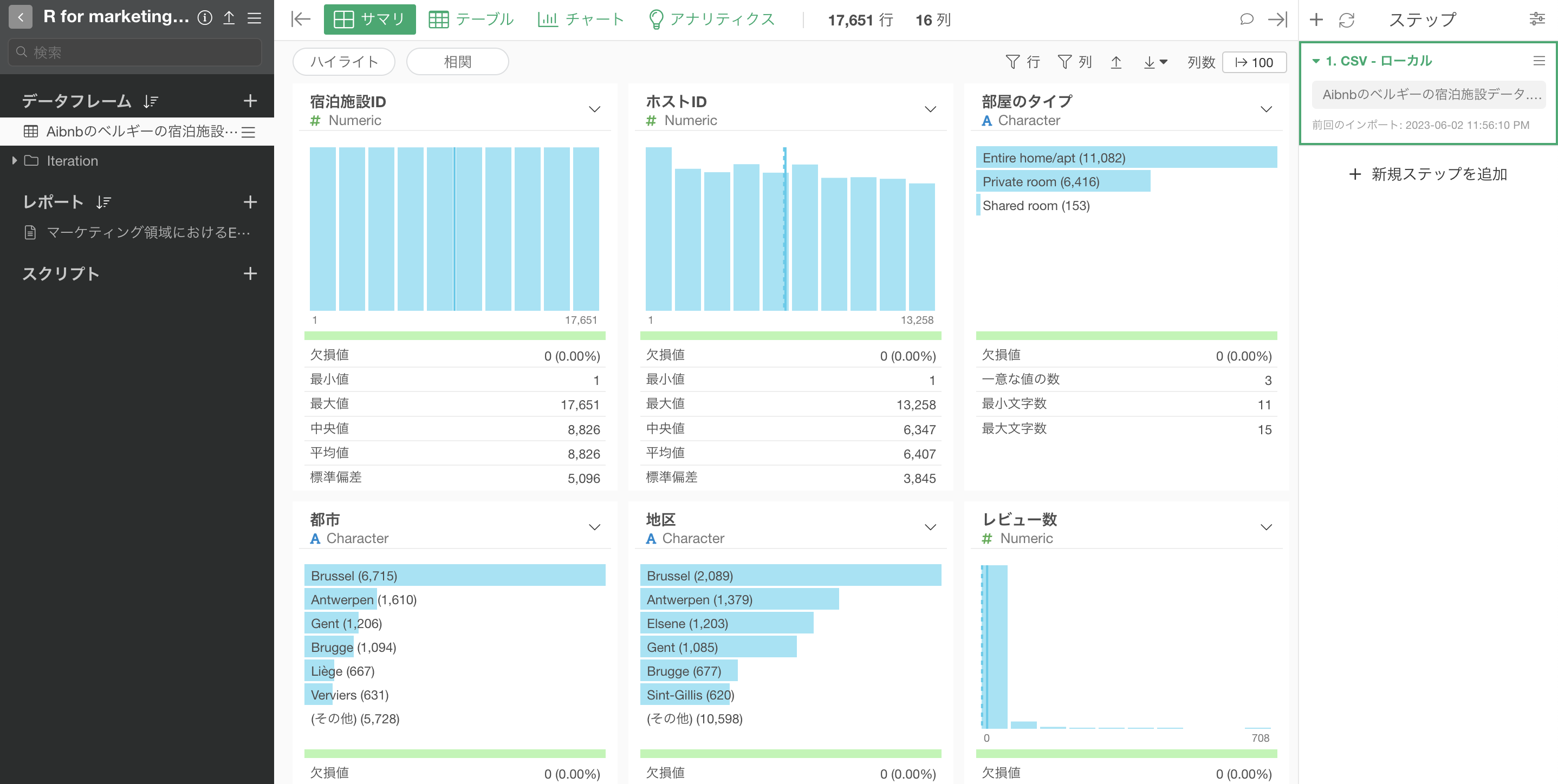
Airbnbのデータをインポートすることができました。
線形回帰(単回帰)
今回は「総合満足度」という変数から「一泊の価格」を予測するシンプルなモデル(単回帰)を作成することから始めます。
チャートから線形回帰を実行する
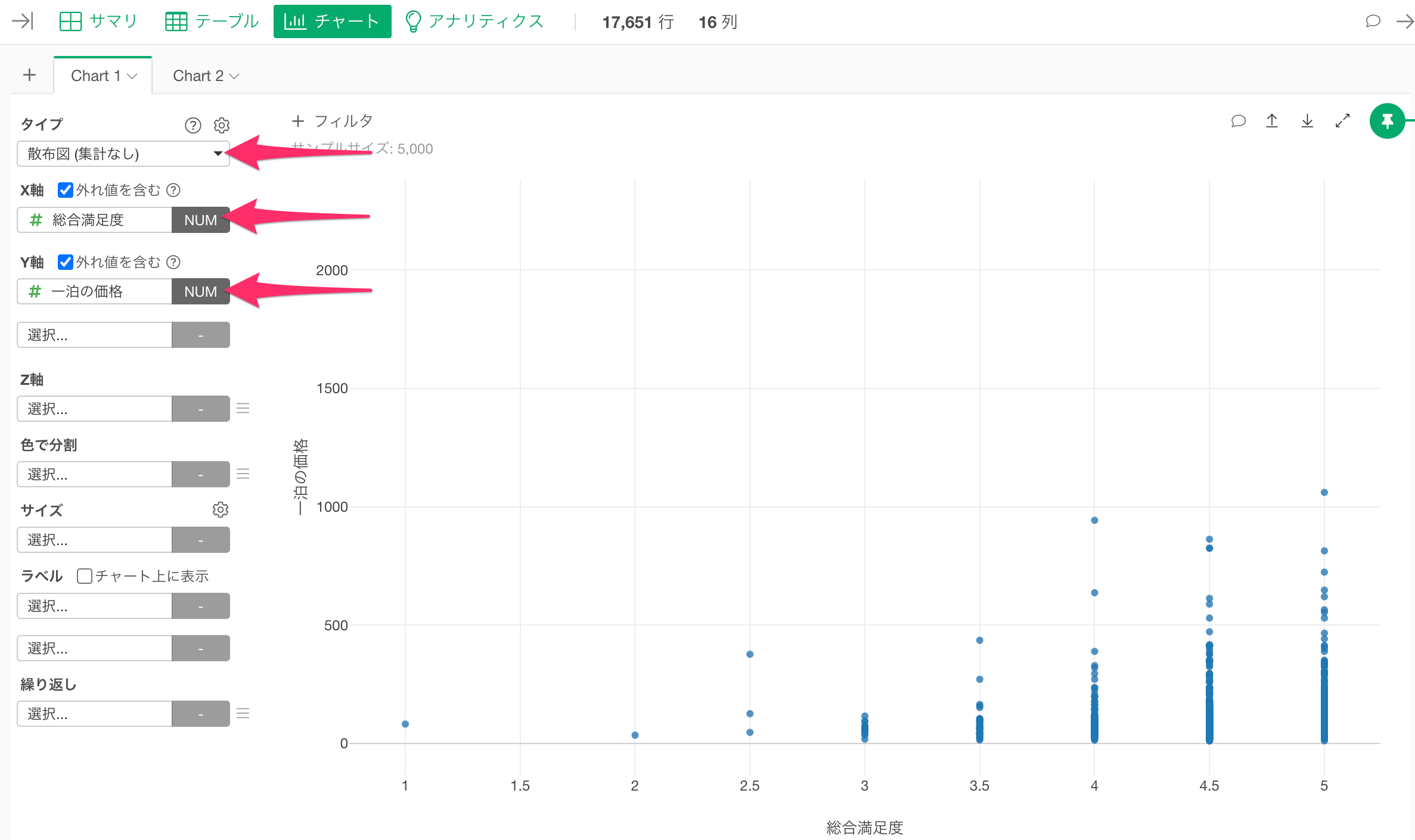
チャート・ビューに移動して、タイプに「散布図(集計なし)」を選択し、X軸に「総合満足度」、Y軸に「一泊の価格」を選択します。
続いて作成した散布図に、線形回帰のトレンドラインを引くために、Y軸のメニューから、「トレンドライン」を選択します。
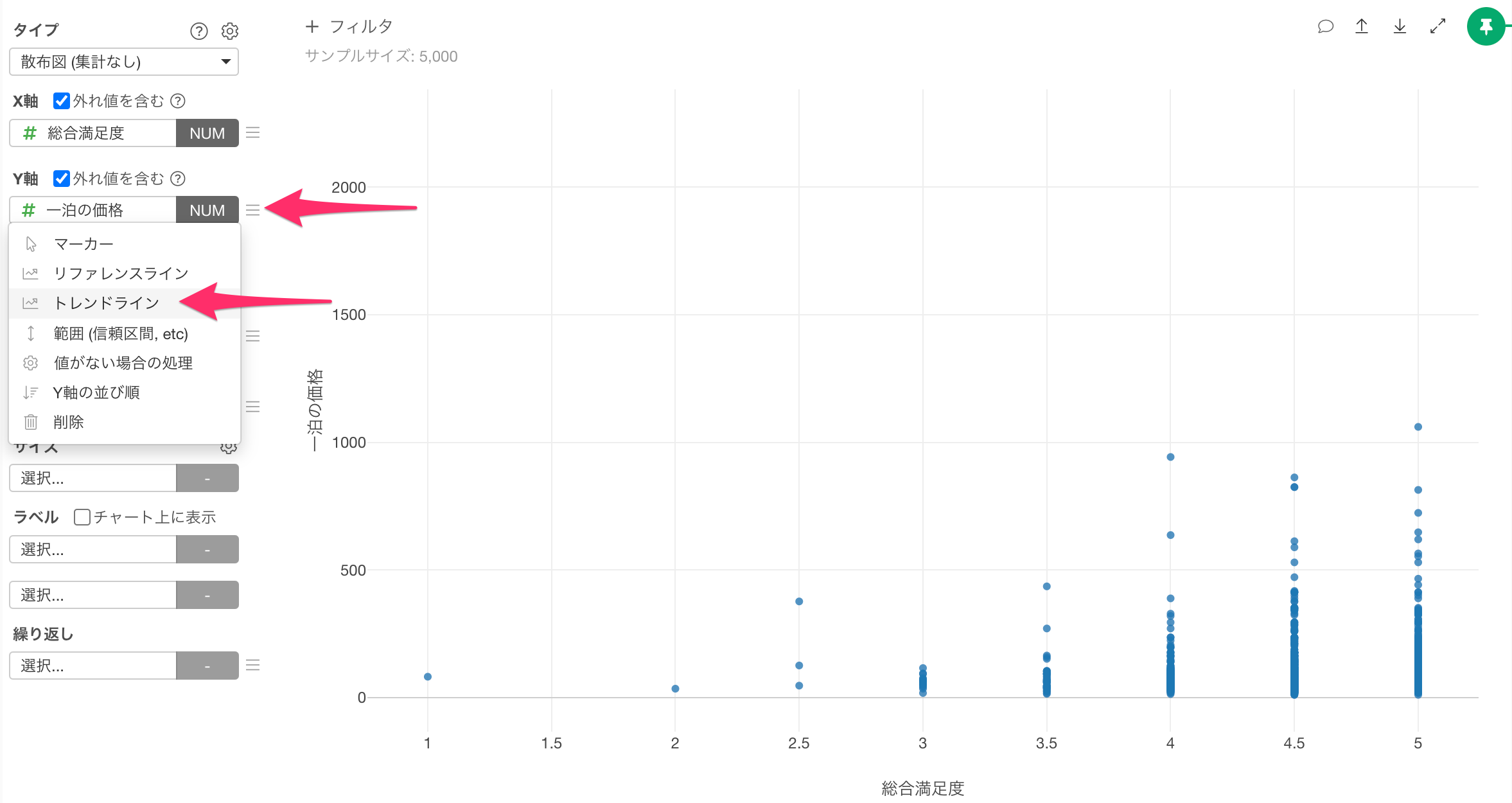
タイプに「線形回帰」を選択し、適用します。
線形回帰のトレンドラインを追加できました。
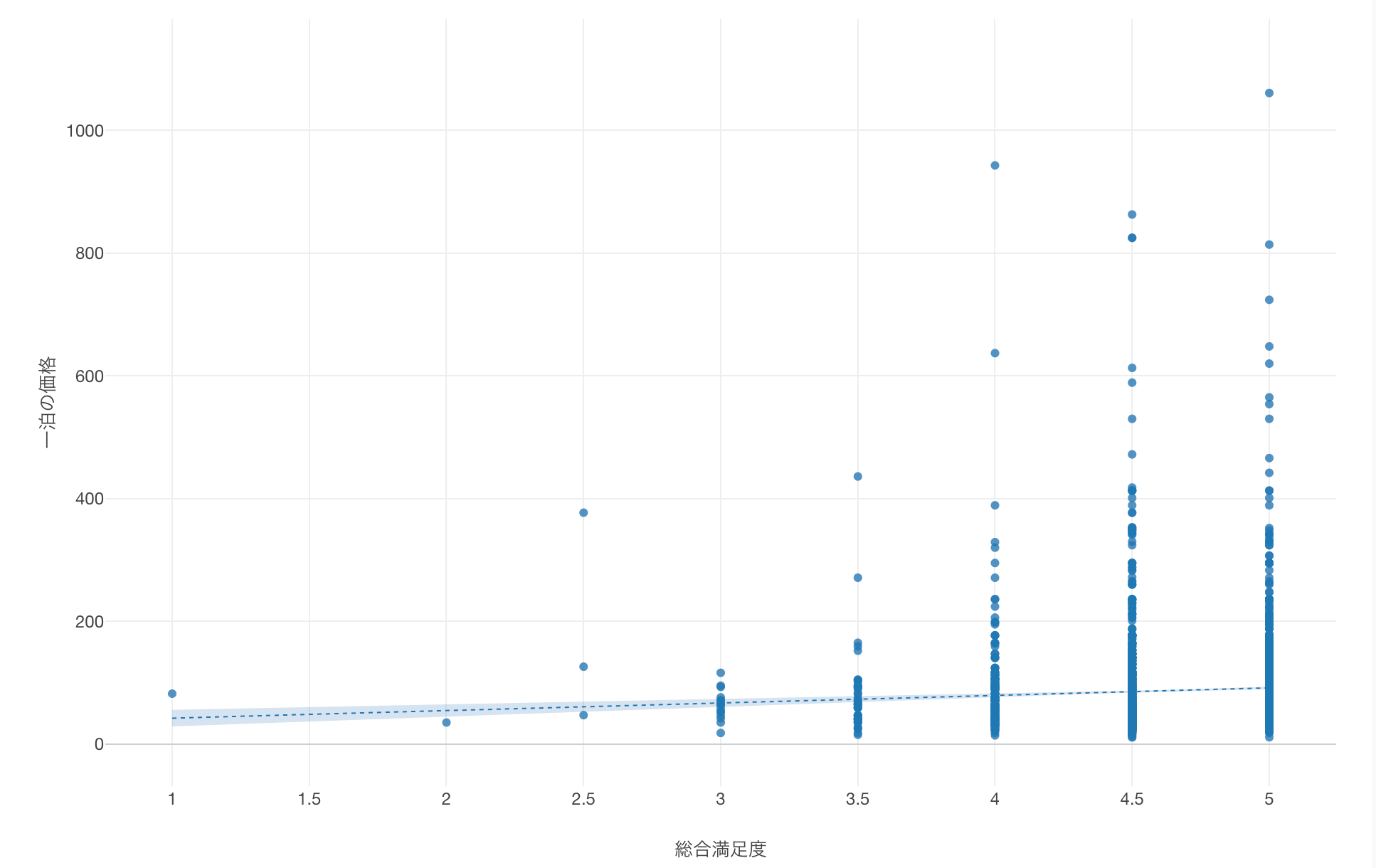
「総合満足度」と「一泊の価格」の関係をわかりやすくするために、チャートの描画エリアをドラッグして拡大します。
チャートを拡大することができました。
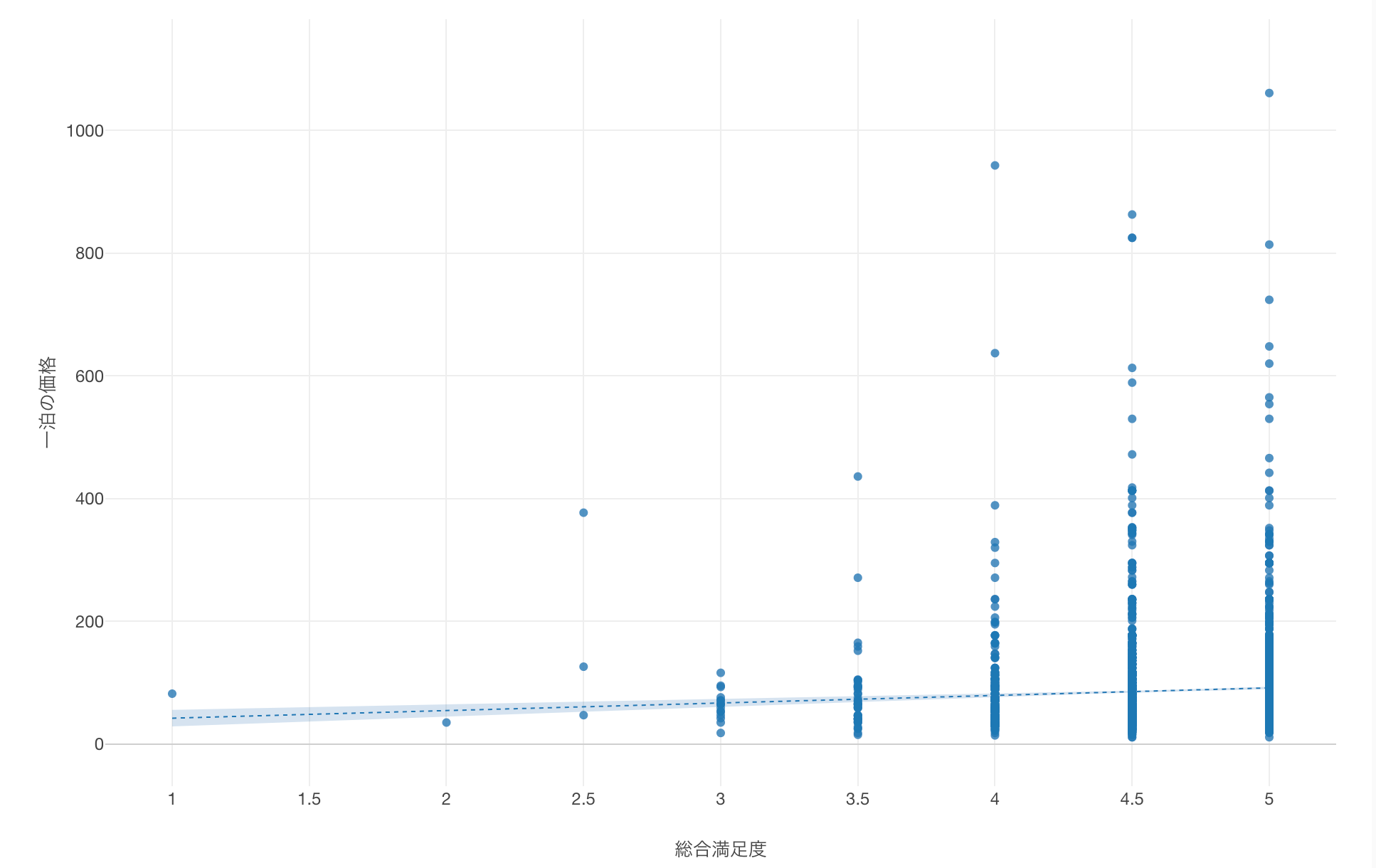
わずかではありますが「総合満足度」が高まると、「一泊の価格」も若干上がる傾向にあることがわかります。
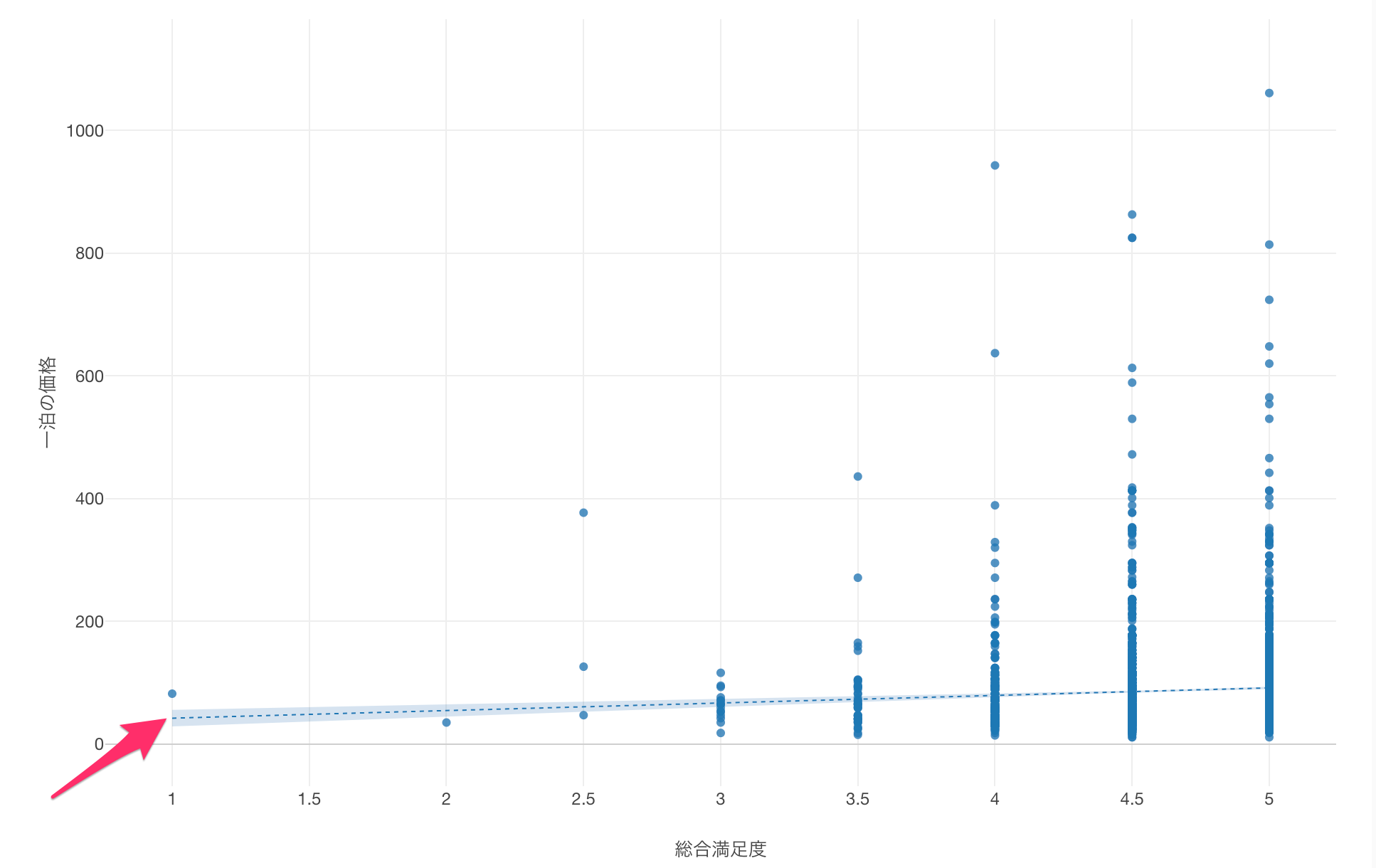
トレンドラインにマウスカーソルを合わせると、線形回帰のトレンドラインの詳細を確認できます。
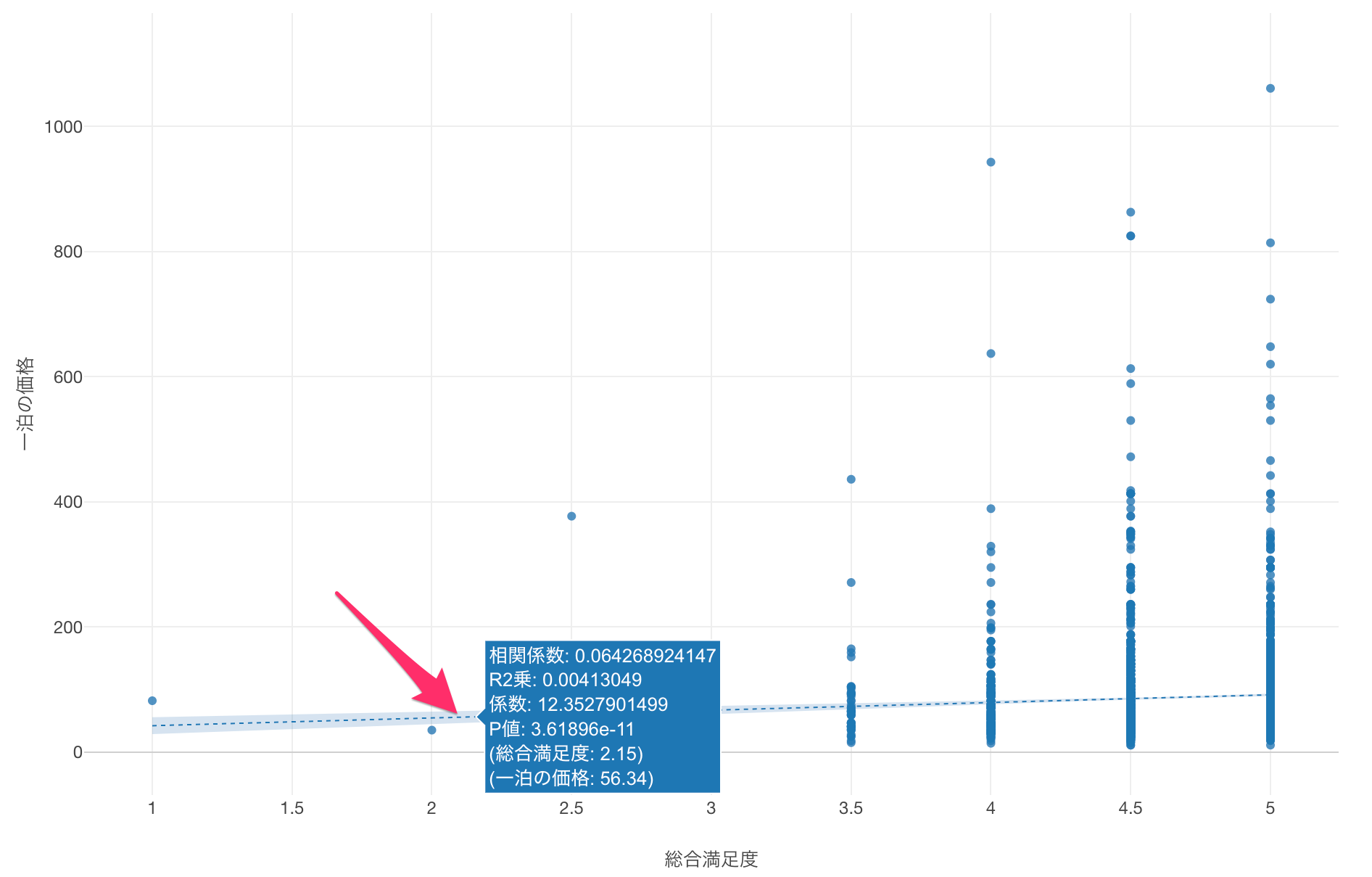
係数が「12.35」であることから、総合満足度が「1」単位増えるごとに、一泊の価格が「12.35」ドル増えることがわかります。
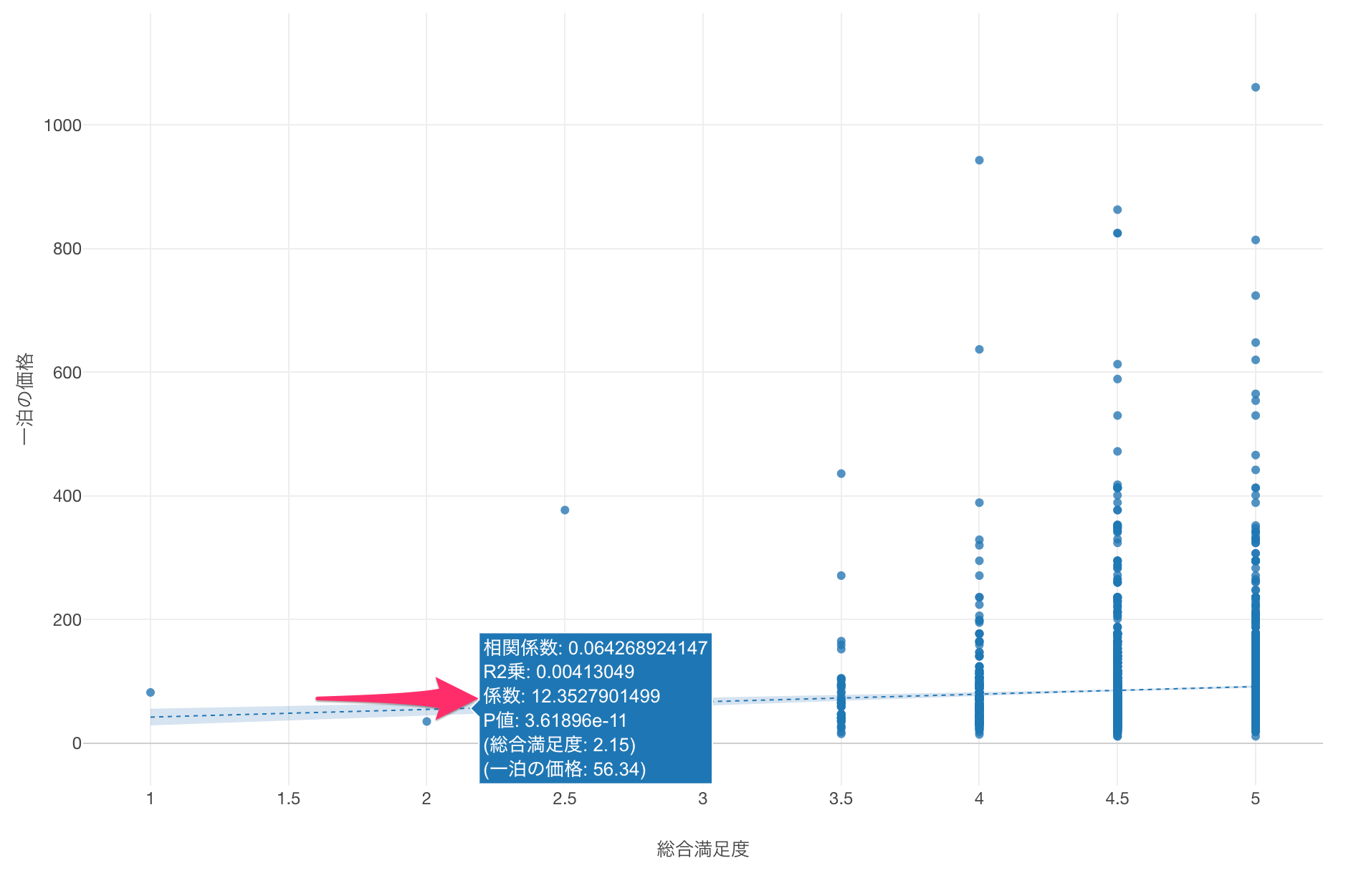
また、「総合満足度」と「一泊の価格」の間には関係がないという帰無仮説を前提としたときに、今回得られているP値は非常に小さい値です。
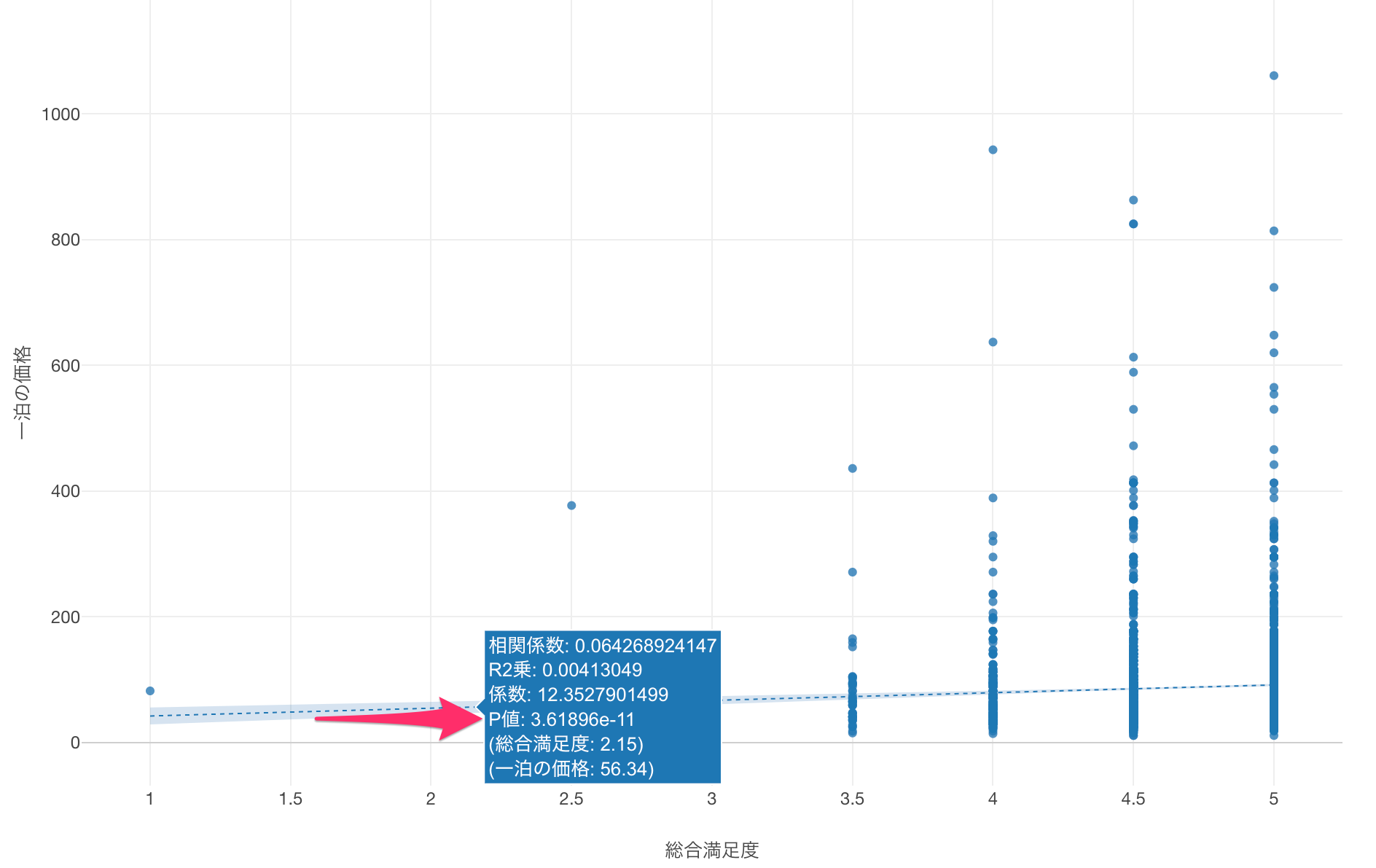
そのため、有意水準を5%とした場合、P値は有意水準値よりも小さいため、帰無仮説を棄却でき、「総合満足度」と「一泊の価格」の関係は有意であることがわかります。
アナリティクスから線形回帰を実行する
続いて、散布図で作成した線形回帰をアナリティクスからも実行します。
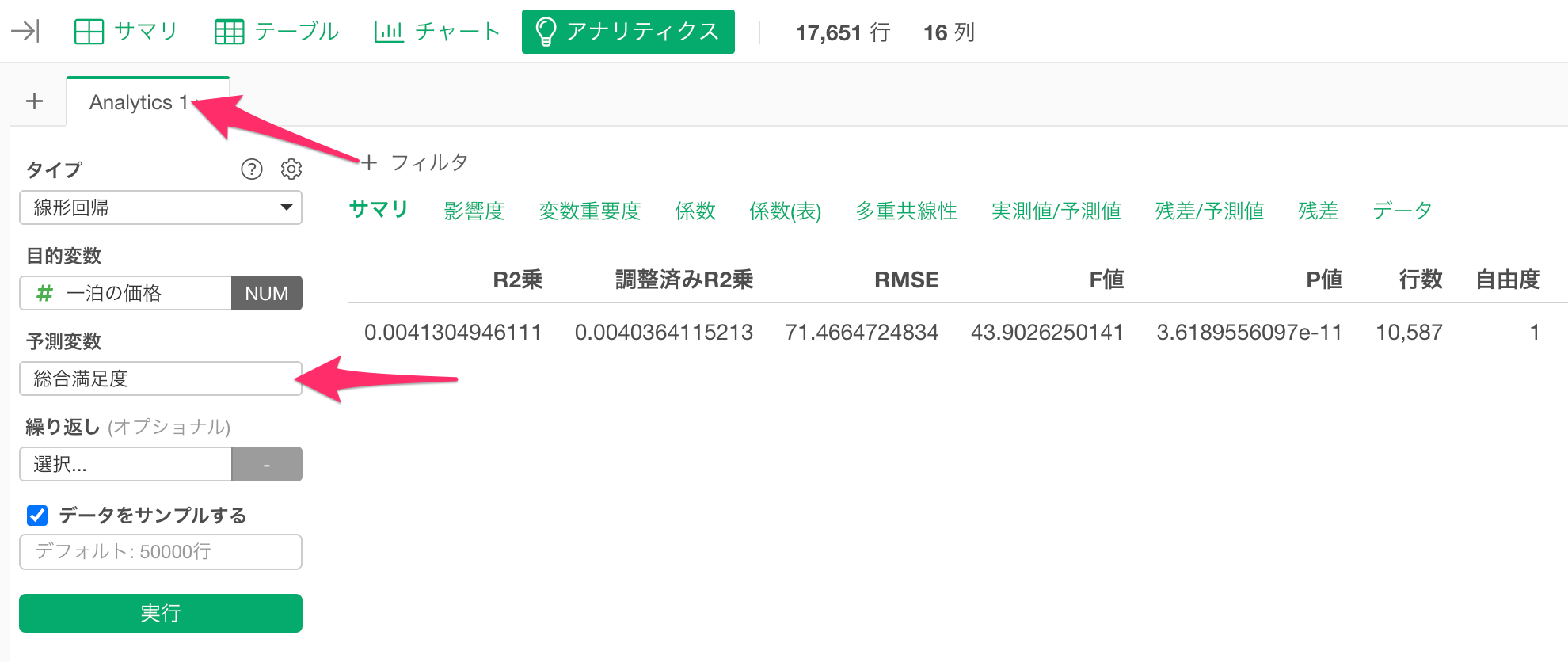
アナリティクス・ビューに移動して、タイプに「線形回帰」、目的変数に「一泊の価格」を選択し、予測変数を選択します。
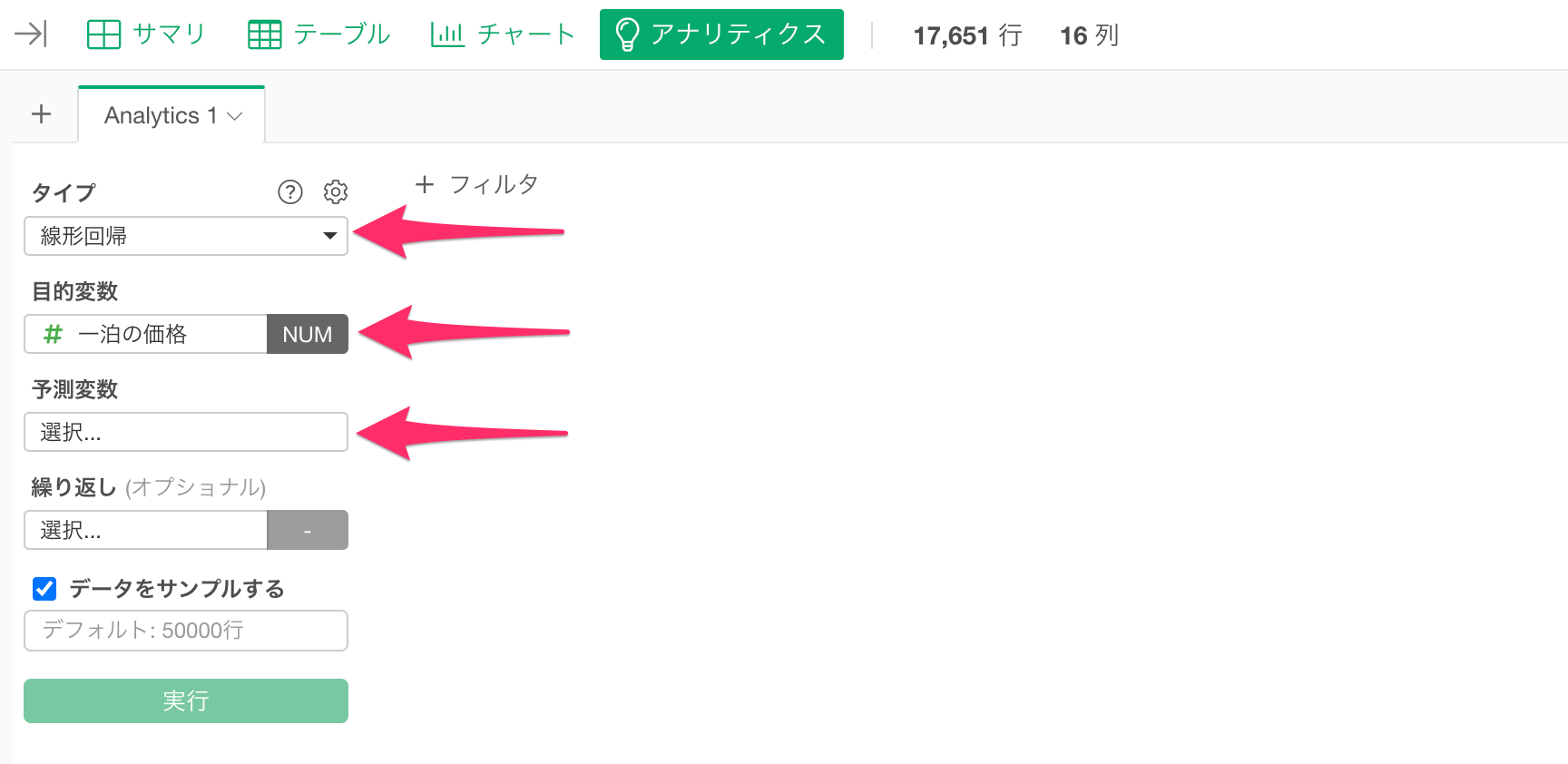
予測変数に「総合満足度」を選択します。
実行ボタンをクリックします。
線形回帰の実行結果が表示されます。
結果の解釈
変数重要度
変数重要度タブでは、複数の変数を予測変数に選択したときに、どの変数が目的変数とより相関が強いのかや、予測する時により重要なのかを調べることができます。
ただし今回は、「総合満足度」という1つの変数を使って、「一泊の価格」を予測しているので、「表示するデータがありません」と表示されます。

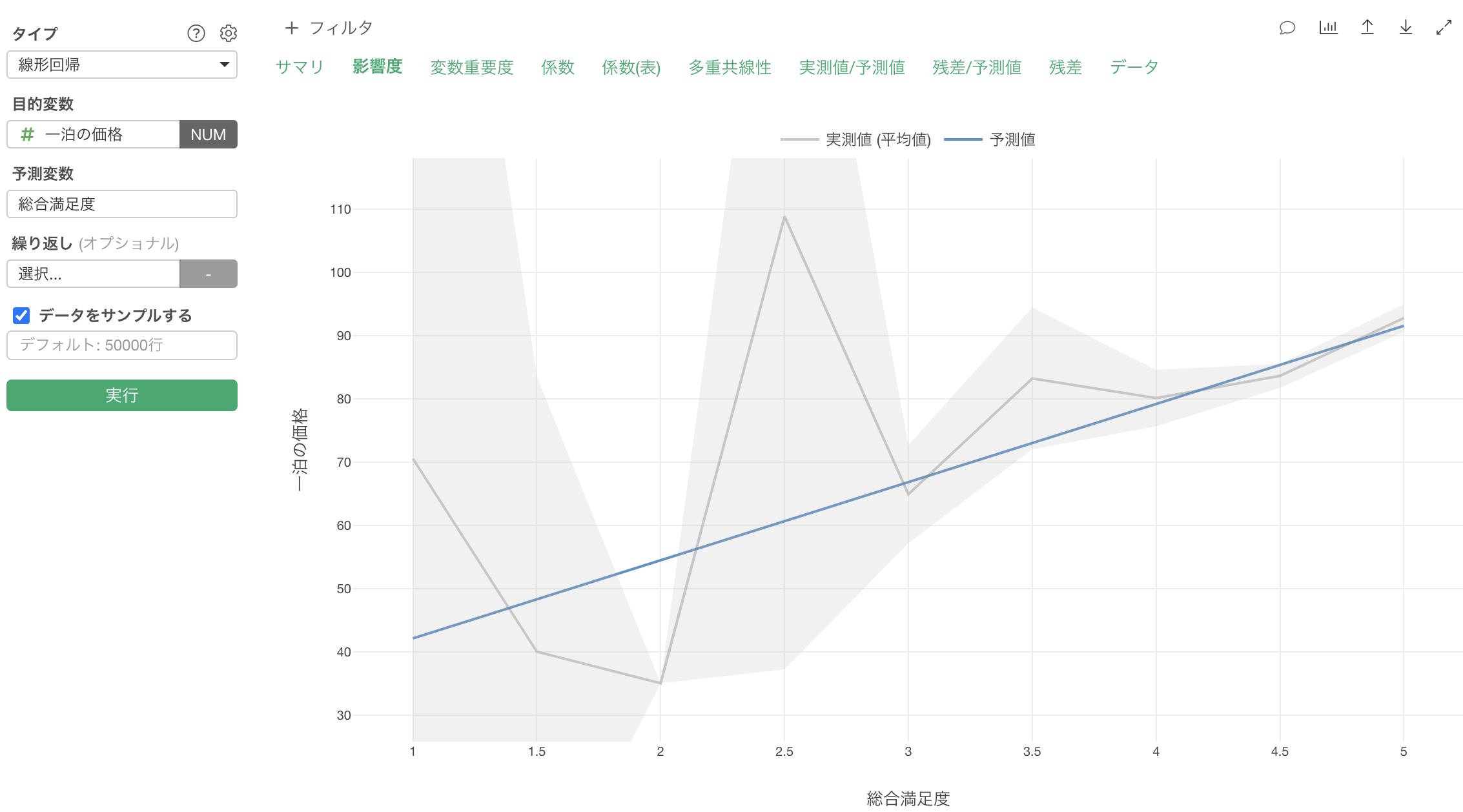
影響度
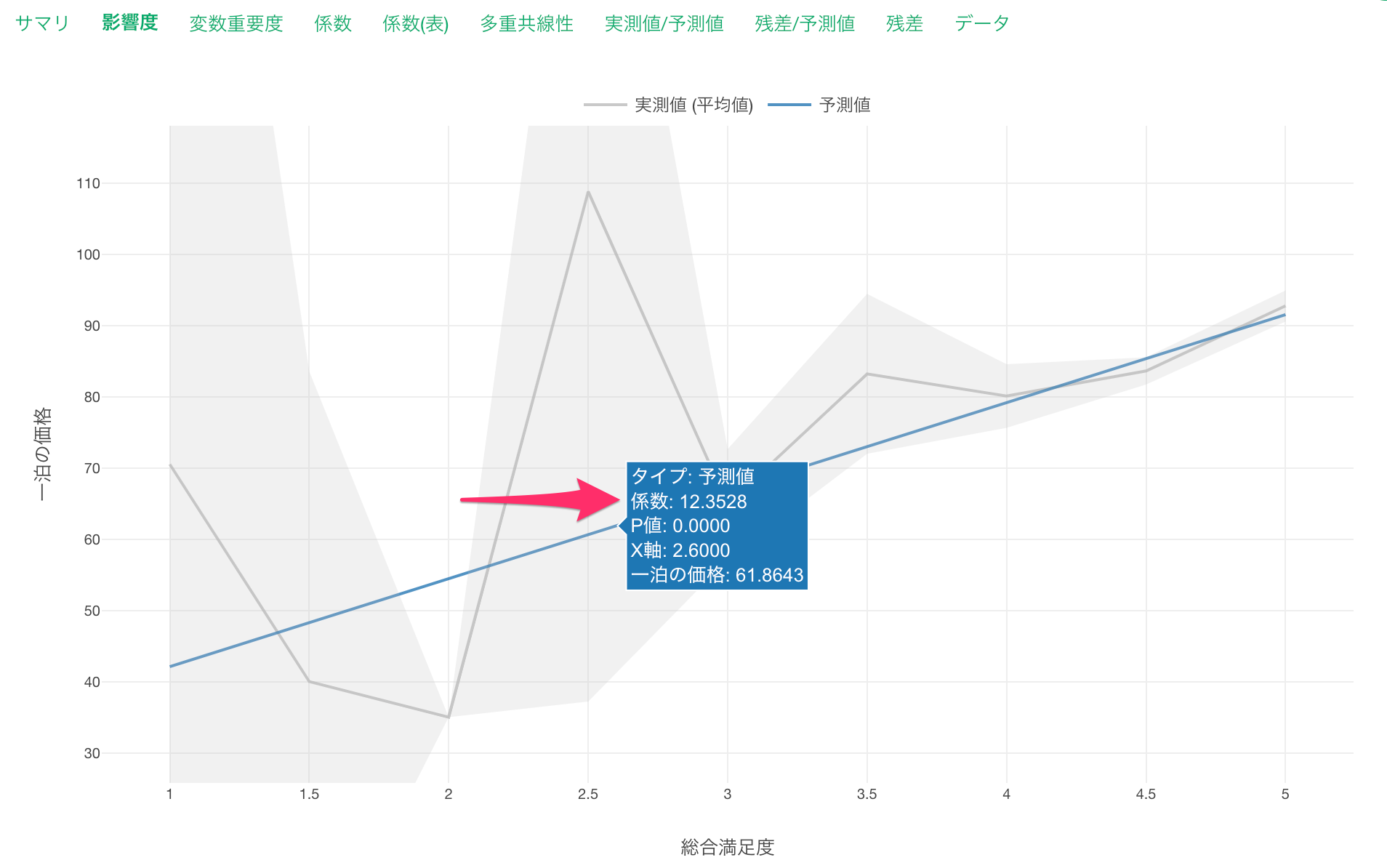
影響度タブでは、それぞれの変数の値が変わると、目的変数の値はどのように変わるのかがわかります。
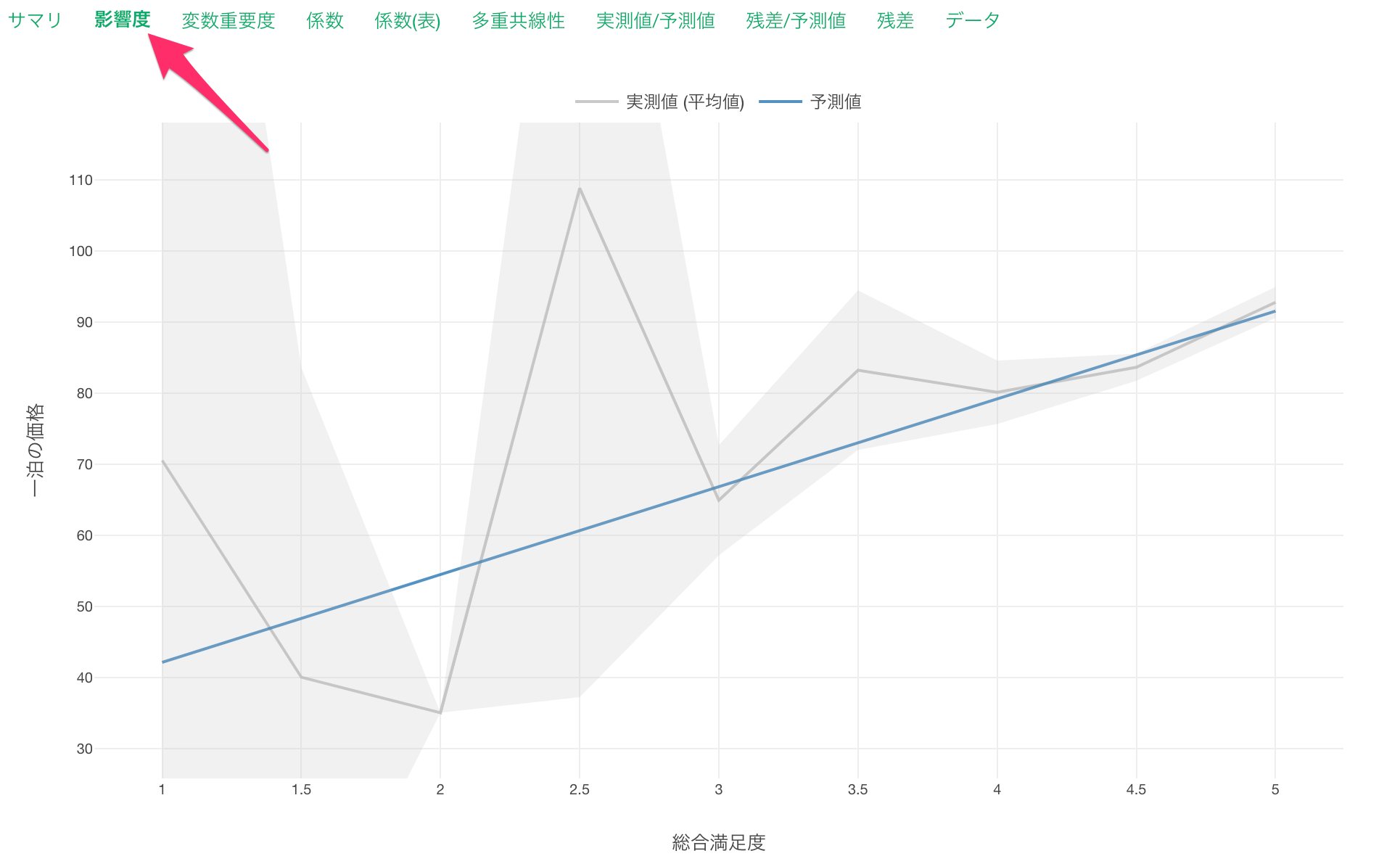
グレーの線は、実測値を表しています。
また青い線は予測値を表します。
作成した線形回帰のモデルは、総合満足度が1単位上がると、一泊の価格が12.35ドル高くなる、と予測していることがわかります。
係数
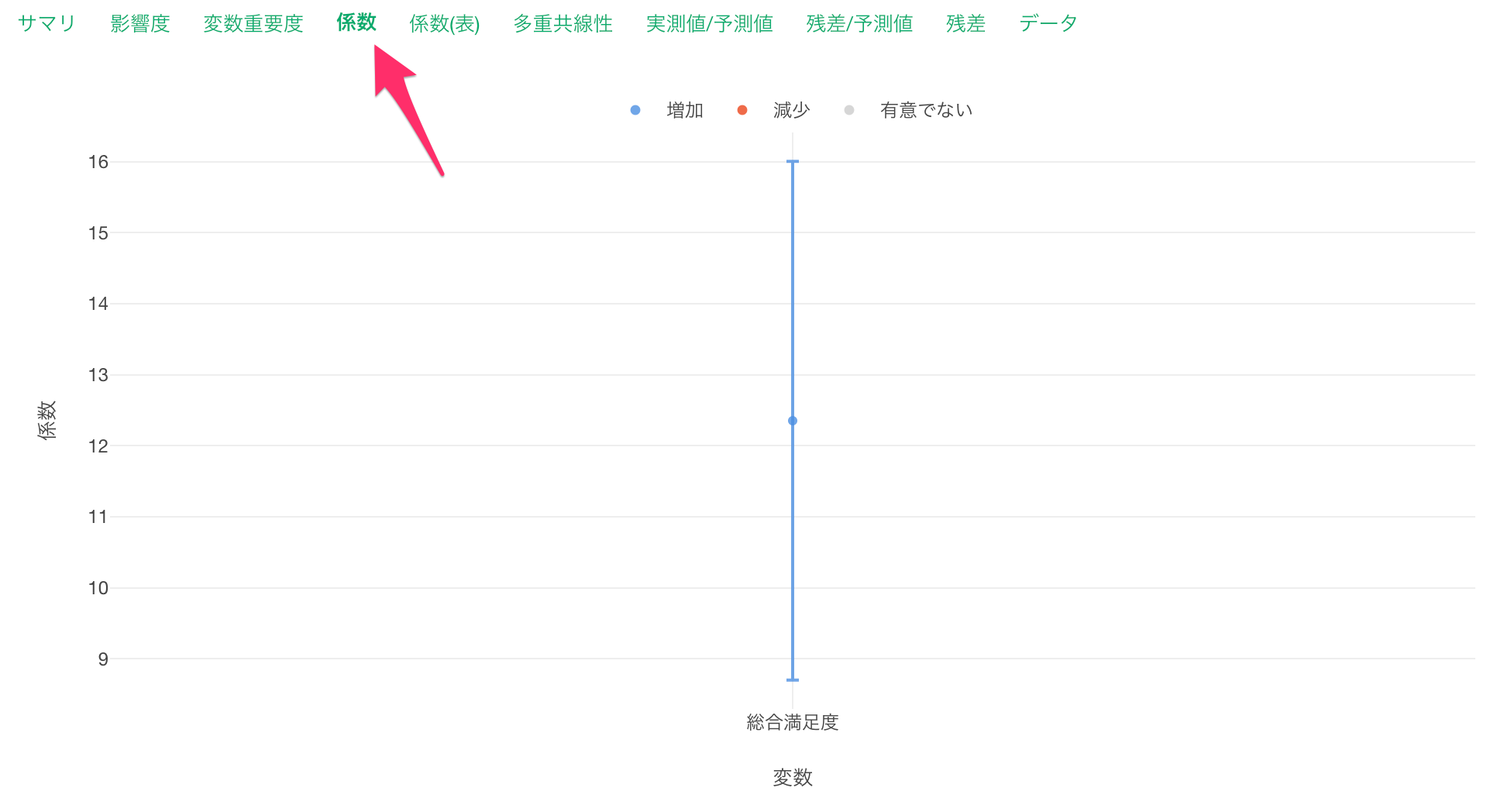
係数タブでは、それぞれの変数の傾きとその信頼区間、有意性がわかります。
係数が増加(青)または減少(赤)の場合は、目的変数である「一泊の価格」との関係が有意な変数で、P値は5%以下です。
これらの変数は係数の信頼区間が0に重なっていない、つまり傾き(係数)が0であることはないと言えます。
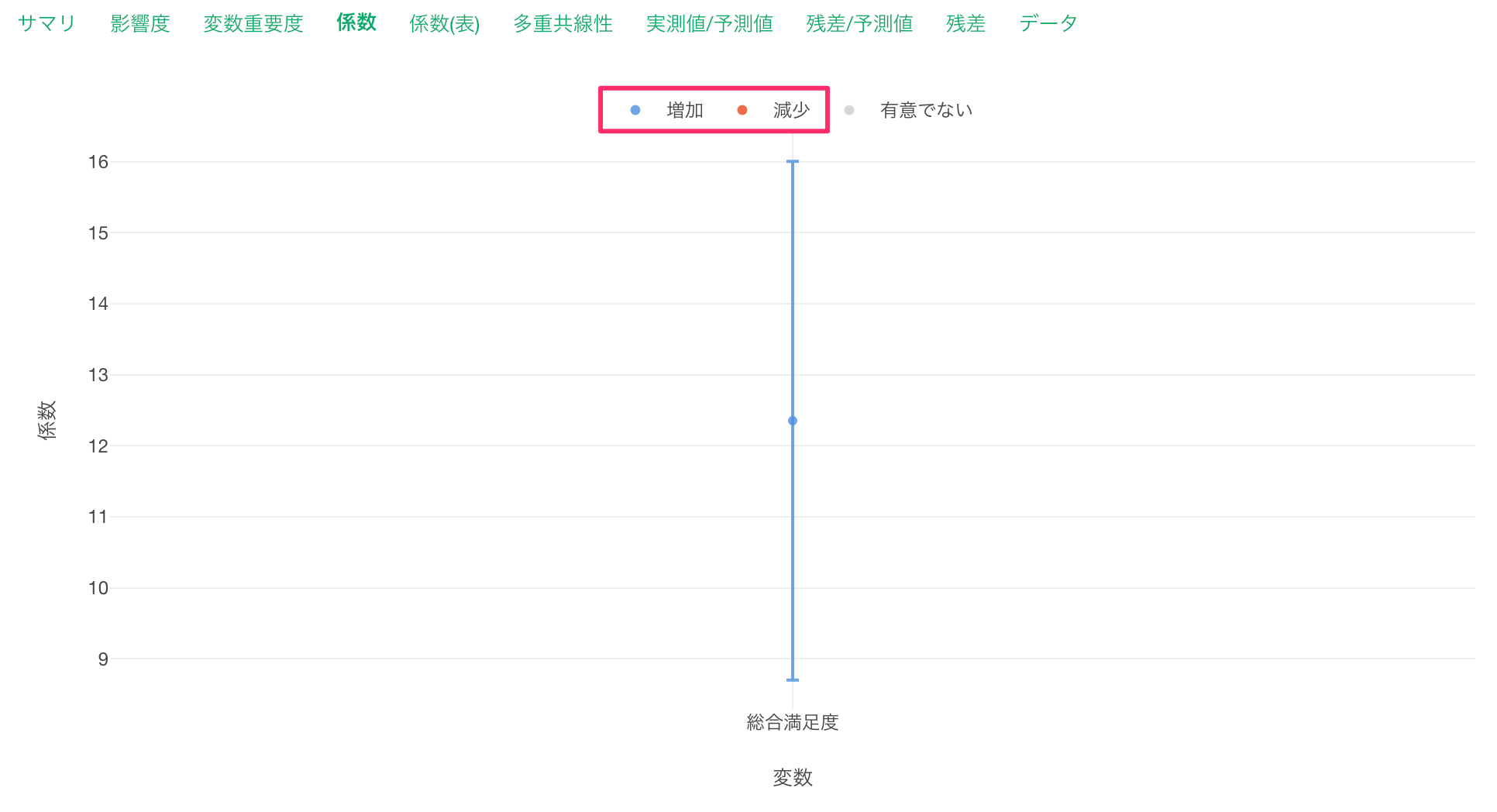
なお、係数がグレーの変数はP値が基準値の5%以上で、統計的に有意であるとは言えない変数です。これらの変数は係数の信頼区間が0に重なっているため、傾きが0の可能性があります。
予測変数(総合満足度)にマウスカーソルを合わせると、係数から総合満足度が1単位が上がると一泊の価格が12.35ドル高くなると期待されることがわかります。

係数表
係数表タブでは、この予測モデルの係数に関する情報を表形式で確認できます。

切片が29.74、総合満足度の係数が12.35であることから、この線形回帰のモデルを数式で表した場合、以下となることがわかります。

一泊の価格 = 12.35(総合満足度の係数)x 総満足度 + 29.74(切片)
サマリ
サマリタブでは、この予測モデルの評価を確認できます。

R2乗はデータの平均からのばらつきをモデルが説明できている割合の指標で、0から1の間の値を取ります。

1に近ければ近いほど、モデルがデータのばらつきをよく説明できていることを示します。
なお、R2乗の意味は指標のガイドからも確認が可能です。

今回のモデルのR2乗は0.004です。このモデルを使うと一泊のばらつきの0.41%を説明できていると言え、「一泊の価格」のばらつきをうまく説明できているとは言えないことがわかります。
一方でP値を確認すると、非常に小さい値になっていることがわかります。

サマリタブで確認できるP値は、「目的変数と予測変数の間には関係がない」という帰無仮説を前提としたとき、このモデルと目的変数の間に見られる関係が観察されうる確率を表しています。
もし、P値が有意水準値よりも小さい場合、帰無仮説を棄却できるため、この関係は有意であり、そうでなければ有意とは言えないという結論になります。
有意水準を5%とした場合、P値は有意水準より低いため、このモデルと目的変数の間に見られる関係は有意ということになります。
線形回帰(多変量解析)
多くの場合、先程のように単一の変数(総合満足度)で「一泊の価格」を予測するのではなく、例えば、「総合満足度」と物件の「レビュー数」を使って「一泊の価格」を予測するモデルを構築する、言い換えれば、複数の変数を使って予測モデルを構築したいことがあります。
そこで、ここからは「総合満足度」と「レビュー数」を使って、「一泊の価格」を予測するモデルを構築していきます。
先程作成した線形回帰のモデルの「予測変数」をクリックします。
列の選択と設定のダイアログが開いたら、「レビュー数」を選択して、予測変数に追加します。
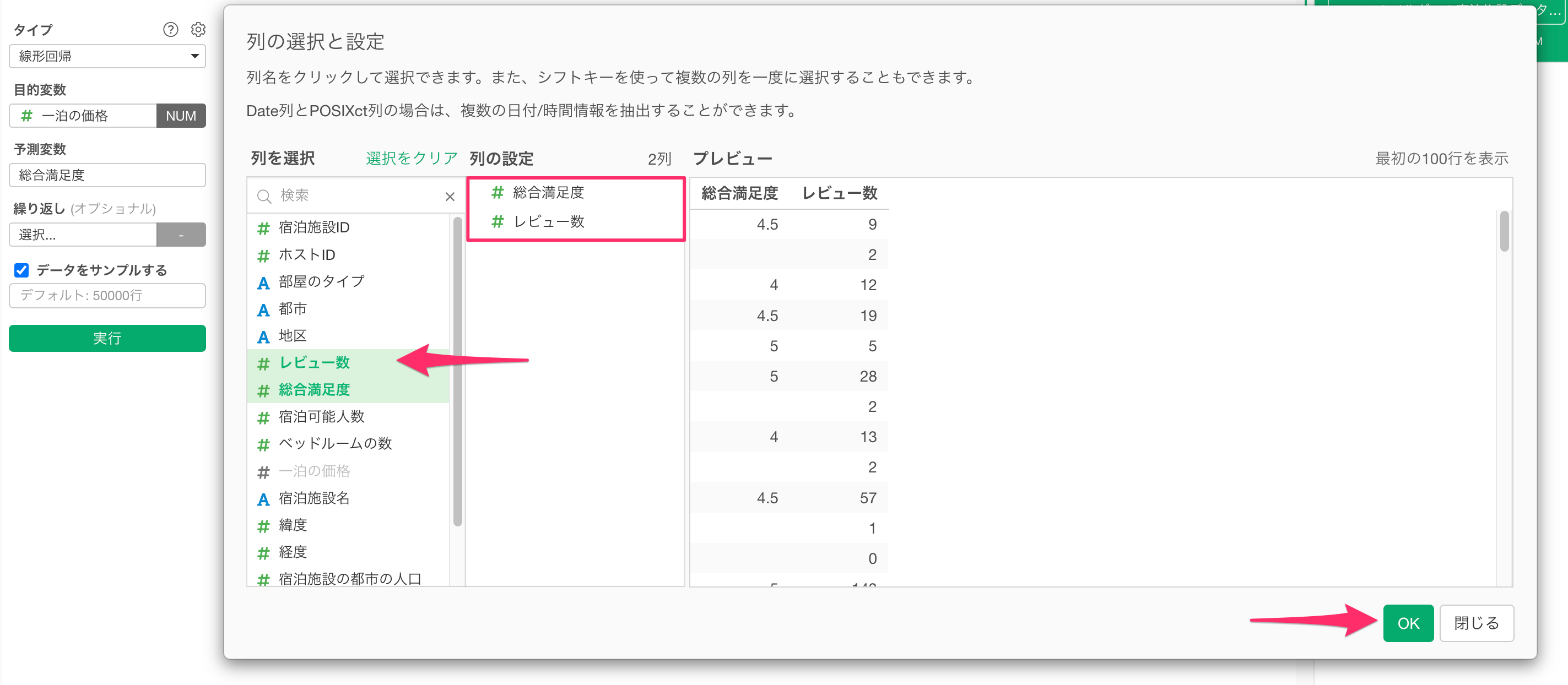
予測変数に「レビュー数」が追加されたことを確認できたら、実行ボタンをクリックします。
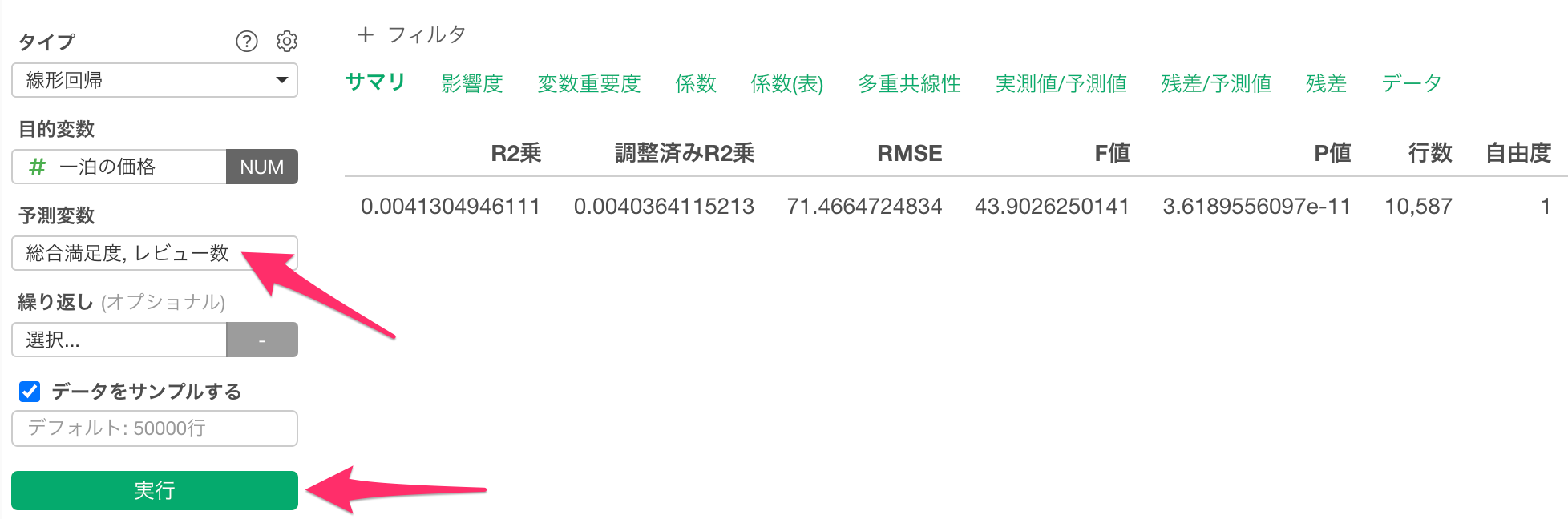
「総合満足度」と「レビュー数」を使って、「一泊の価格」を予測する線形回帰のモデルを構築できました。
結果の解釈
変数重要度
先程紹介したように、変数重要度タブでは、どの変数が目的変数とより相関が強いのか、予測をする時により重要なのかを調べることができます。
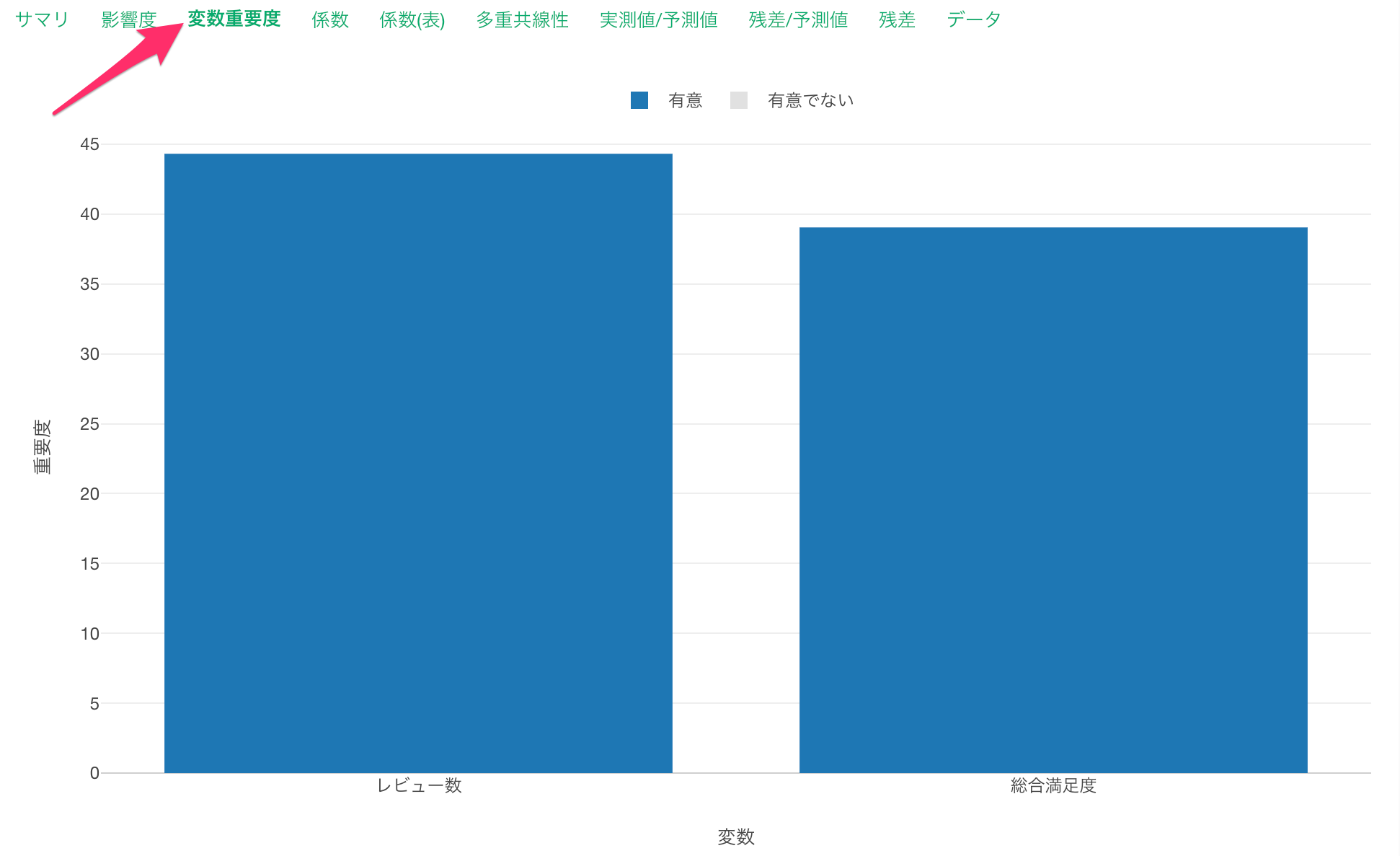
総合満足度よりもレビュー数の方が、給料の予測に重要な変数であることがわかります。
影響度
影響度タブではレビュー数が増えると、一泊の価格が低くなる関係があることがわかります。
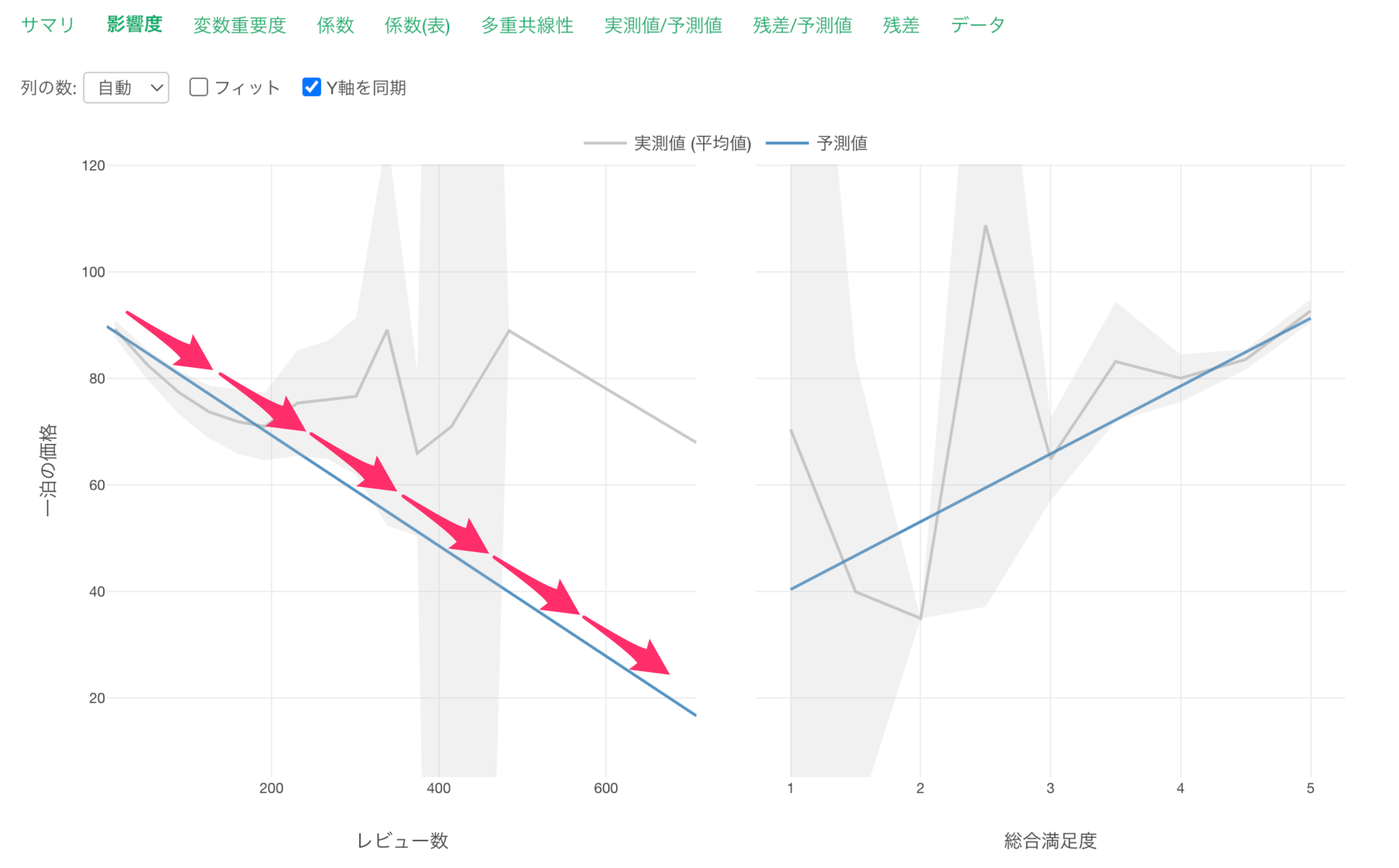
他の変数が一定だった時に、レビュー数が1上がると一泊の価格が0.1ドル下がる関係があるようです。
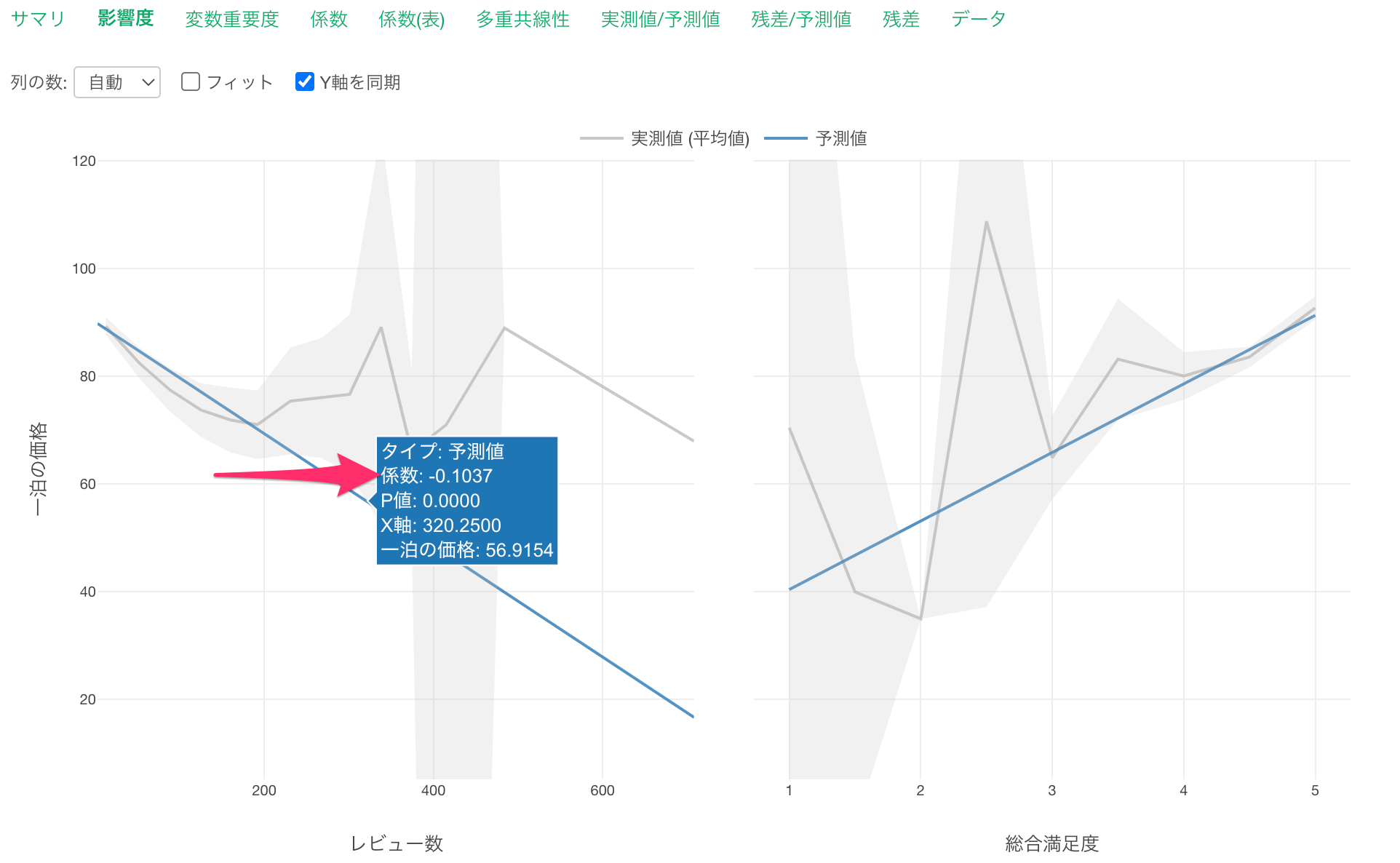
また、総合満足度が増えると、一泊の価格が高くなる関係があることがわかります。
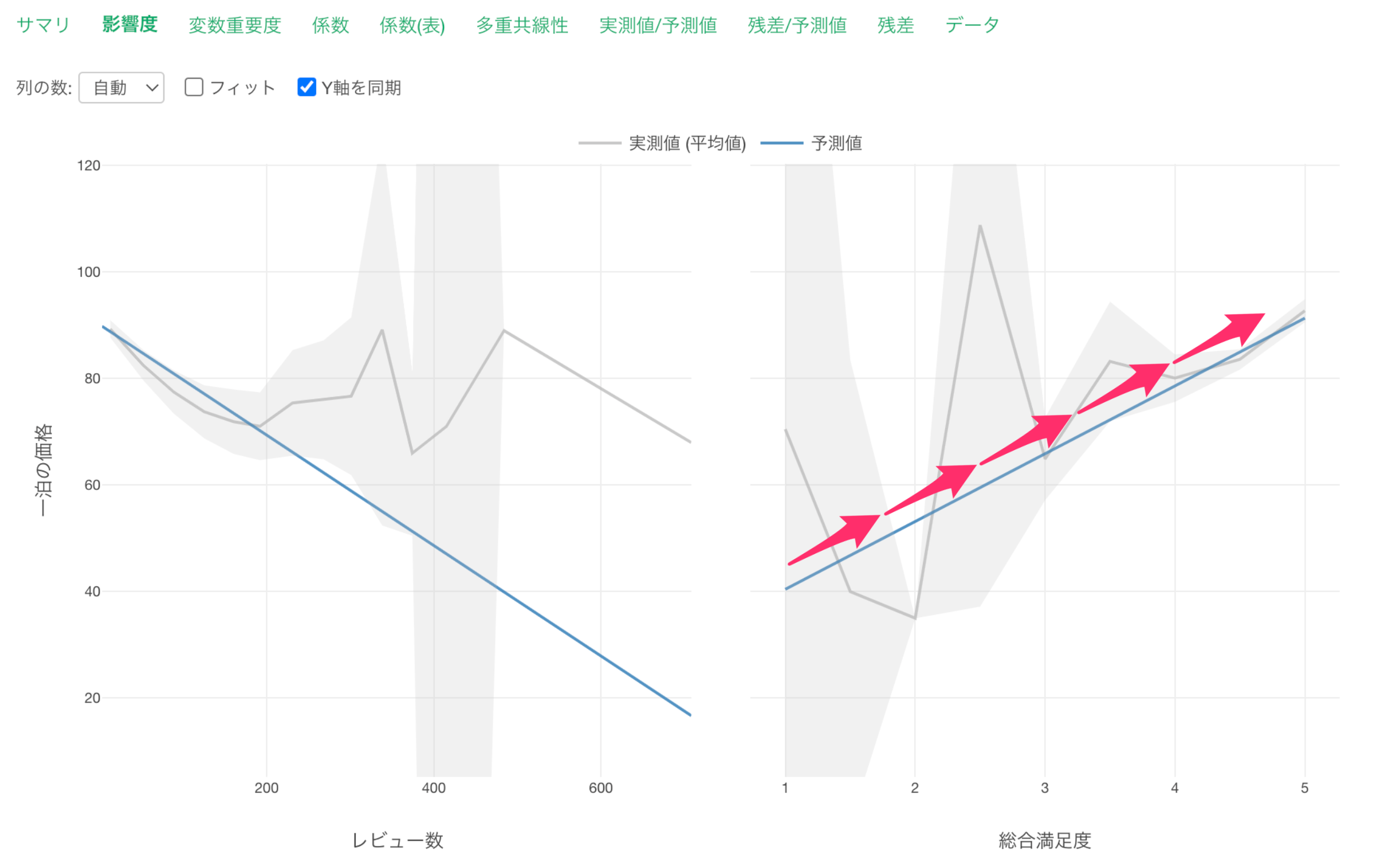
他の変数が一定だった時に、総合満足度が1上がると一泊の価格が12.72ドル上がる関係があるようです。
係数
係数タブを確認すると、「総合満足度」が増加(青)、「レビュー数」が減少(赤)のため、いずれも目的変数である「一泊の価格」との関係が有意な変数で、P値は5%以下であることがわかります。
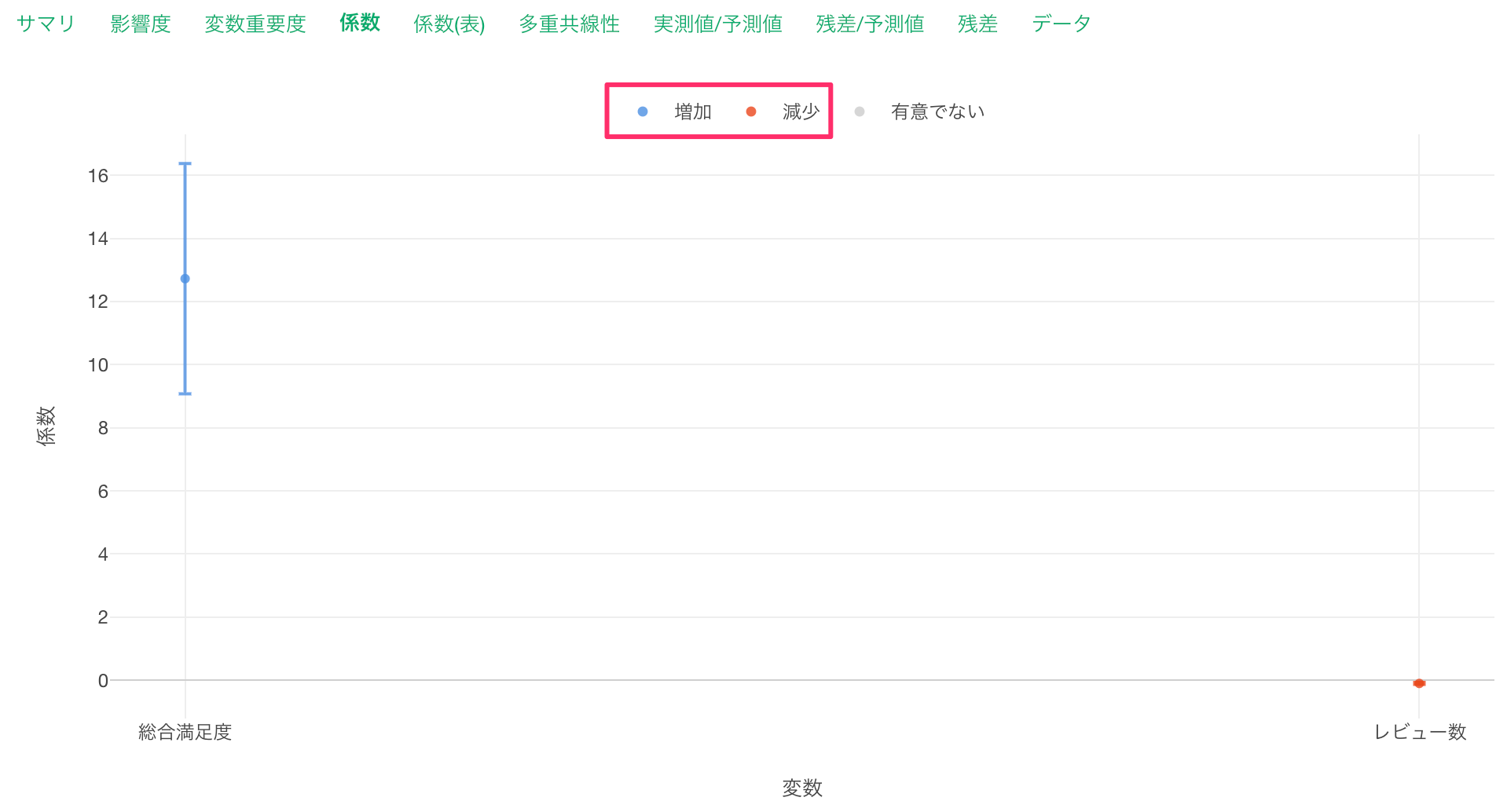
これらの有意な変数は係数の信頼区間が0に重なっていない、つまり傾きが0であることはないと言えます。
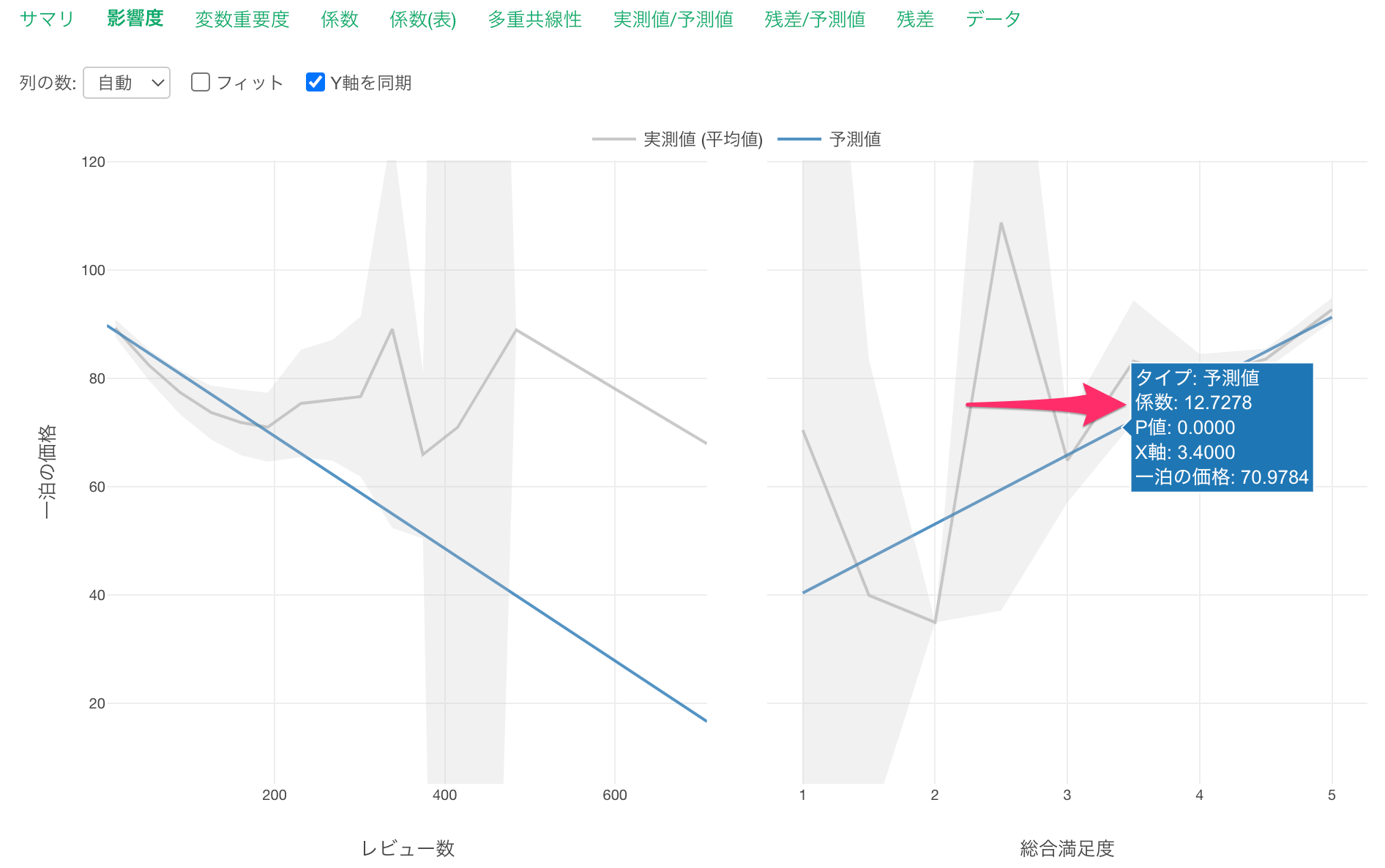
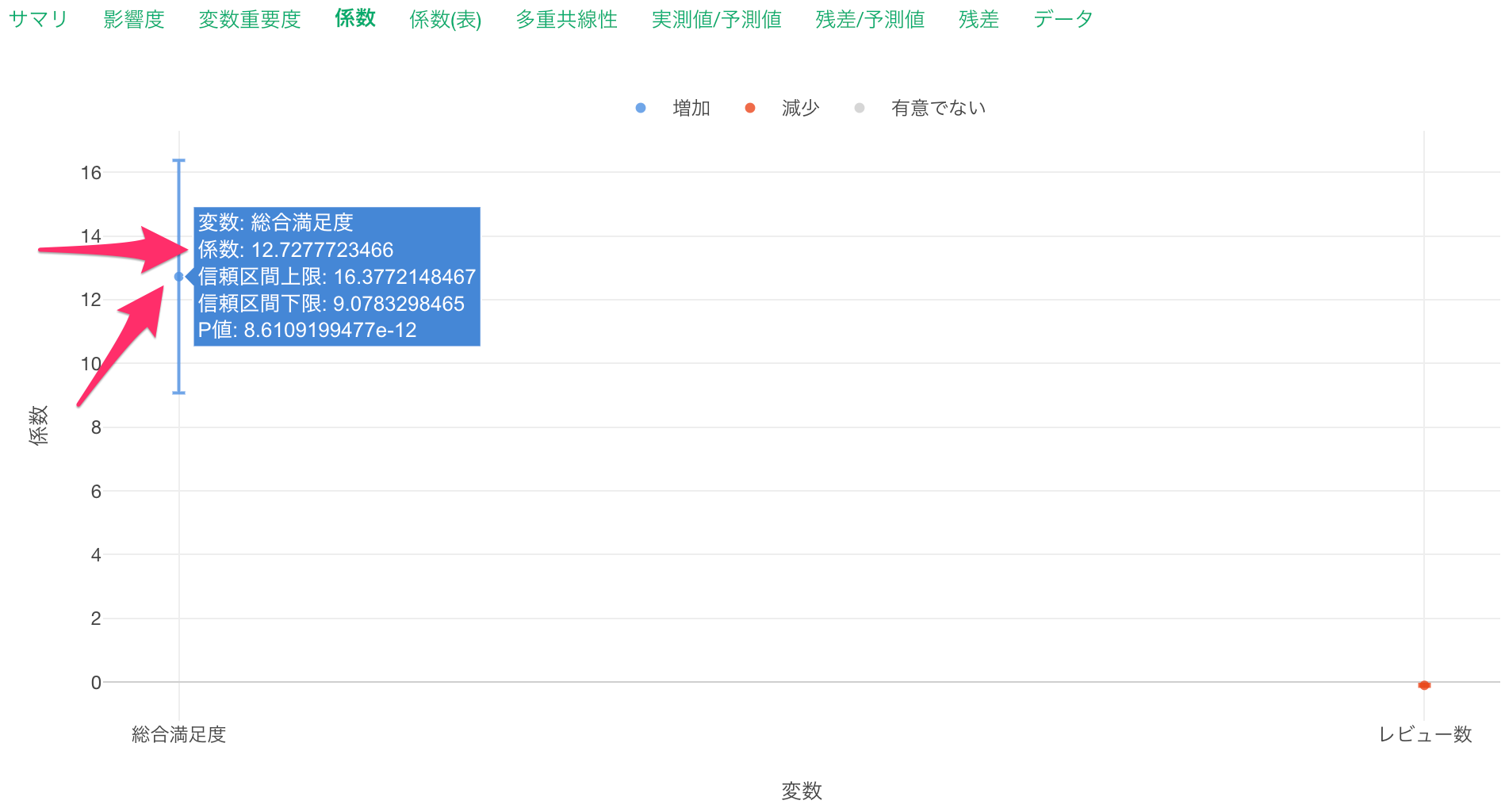
また総合満足度にマウスカーソルを合わせると、係数から、総合満足度が1上がると一泊の価格が12.72ドル高くなると期待されることがわかります。
またレビュー数にマウスカーソルを合わせると、係数から、レビュー数が1上がると一泊の価格が0.1ドル低くなる(-0.1)ことがと期待されます。

係数表
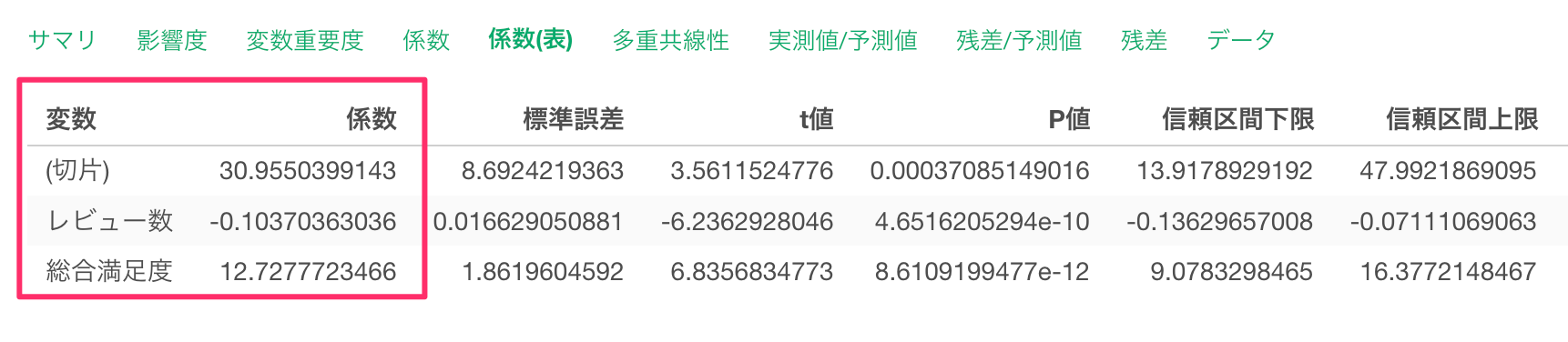
係数表を確認すると、切片が30.96、レビュー数の係数が-0.10、 総合満足度の係数が12.72であることから、この線形回帰のモデルを数式で表した場合、以下となることがわかります。
一泊の価格 = -0.1 x レビュー数 + 12.72(総合満足度の係数)x 総合満足度 + 30.96(切片)
サマリ

R2乗が0.0077のため、このモデルを使うと一泊の価格ばらつきの0.77%を説明できていると言えます。
R2乗は1に近ければ近いほど、モデルがデータのばらつきをよく説明できていることを示しているため、総合満足度だけで一泊の価格を予測しているときよりも、ばらつきをうまく説明できているものの、こちらのモデルでも「一泊の価格」のばらつきを、うまく説明できているとは言えないことがわかります。
また、P値を確認すると非常に小さい値です。

有意水準を5%とした場合、P値は有意水準より低いため、このモデルと目的変数の間に見られる関係は有意ということになります。
多重共線性
ところで、複数の予測変数を使って線形回帰などの予測モデルを構築するときに、気を付けなければいけない、多重共線性の問題があります。
予測変数の間にあまりにも強い相関関係がある場合、モデルの予測変数の係数が定まらなくなってしまい、分析結果が不安定になってしまうのが多重共線性の問題です。
一般的に、この多重共線性の問題を解決するためには、予測変数に選択した変数間の相関関係を調べ、相関関係の強い変数を予測変数から除くことになります。
しかし、Exploratoryでは線形回帰の多重共線性タブから、多重共線性の問題が起きているかどうかを確認して、除外する予測変数を決めることが可能です。
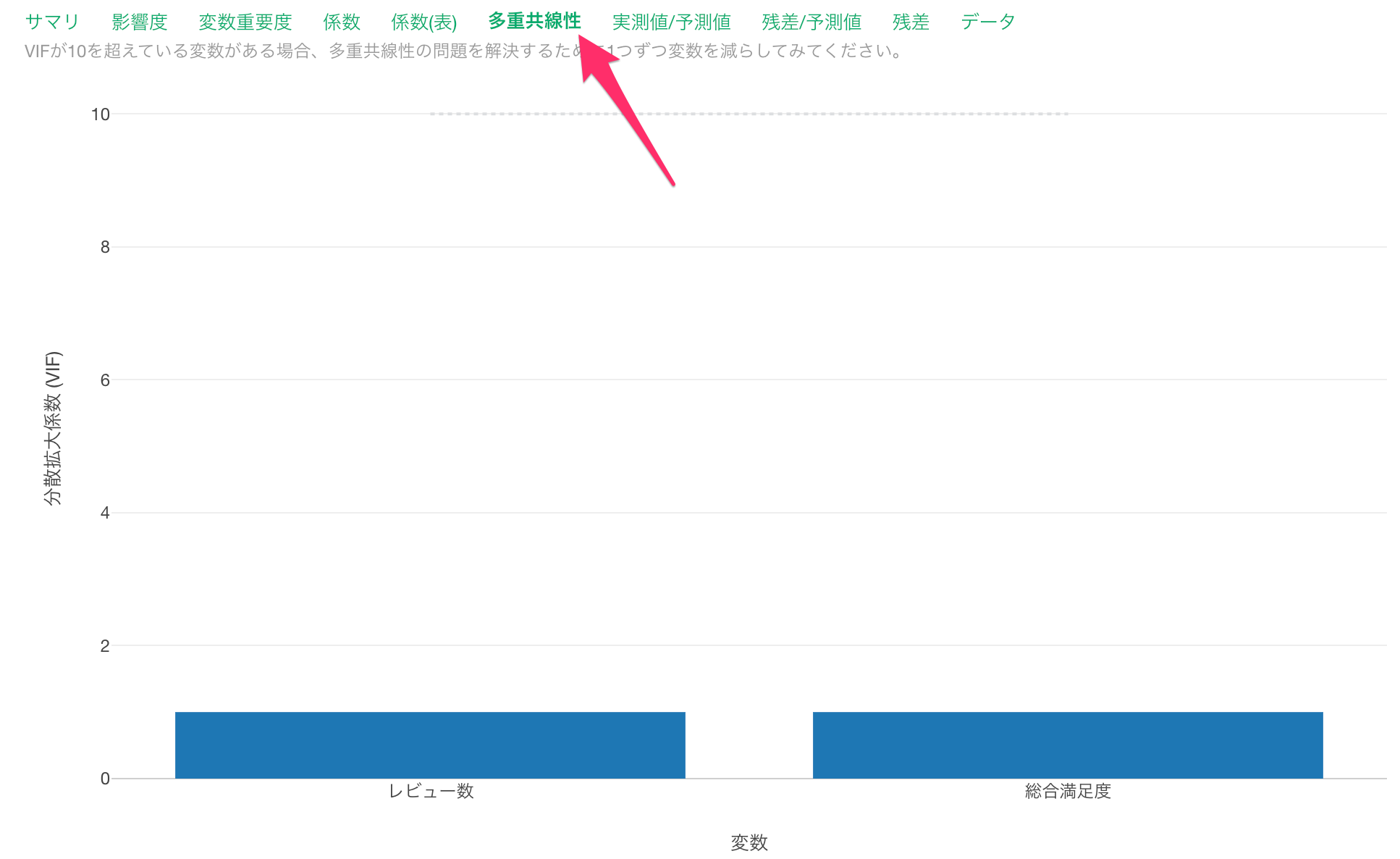
多重共線性のタブでは、各予測変数の分散拡大係数(VIF/Variance Inflation Factor)という指標が計算されています。
分散拡大係数が10を超える変数があった場合、多重共線性の問題が発生していることになり、一般的には、VIFが10を超えている変数を除きます。(多重共線の詳細についてはこちらをご参考ください。)
今回はVIFが10を超える変数はないため、多重共線性の問題は生じていないことになります。
そのため、これまで分析結果の解釈に問題がなかったことを確認できました。
マーケティング・アナリティクス・トレーニング

効果的なマーケティング活動を行うために必要なデータ分析手法を、見込みまたは既存顧客の購買、属性、行動に関するデータを使い、実際に手を動かしながら短期間で効率的に習得していただくためのトレーニングを開催しています。
データドリブンなマーケティング活動を行うために必要なデータサイエンスの手法を短期間で習得したい方は、ぜひこの機会に参加をご検討ください!