K-Meansクラスタリングの紹介
クラスタリングとは、データの中にある共通な部分を持つグループにデータを分類する手法です。
今回は、クラスタリングの代表的な手法であるK-MenasクラスタリングをExploratoryで実行する方法についての紹介となりますが、これによって何ができるのか簡単な例を使ってみていきましょう。
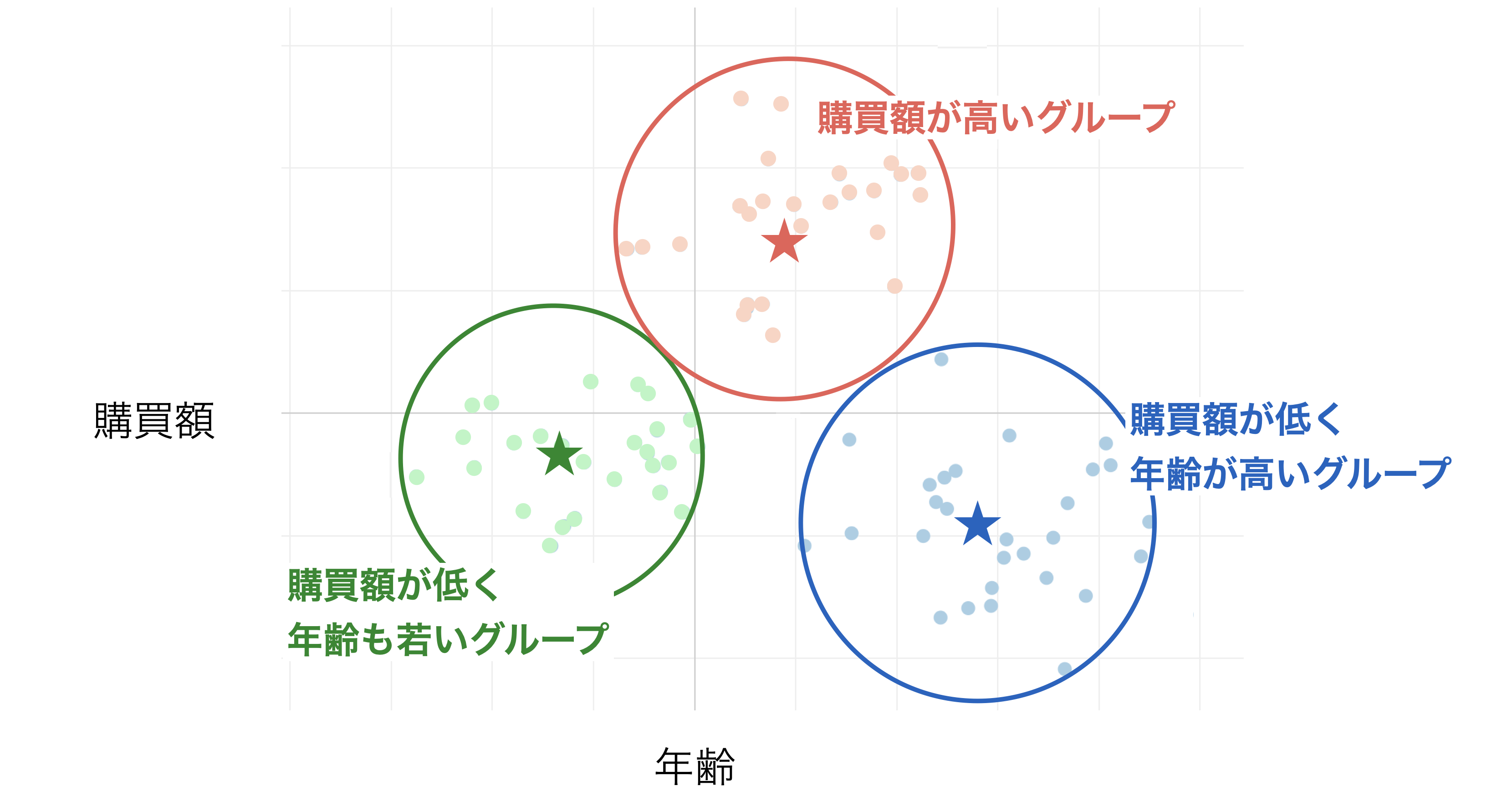
例えば、顧客一人当たりの年齢と購買額の関係をプロットした散布図があったとします。
K-Menasクラスタリングを使うことで、年齢と購買額の値をもとにグループ分けすることができます。

必要なデータの形式
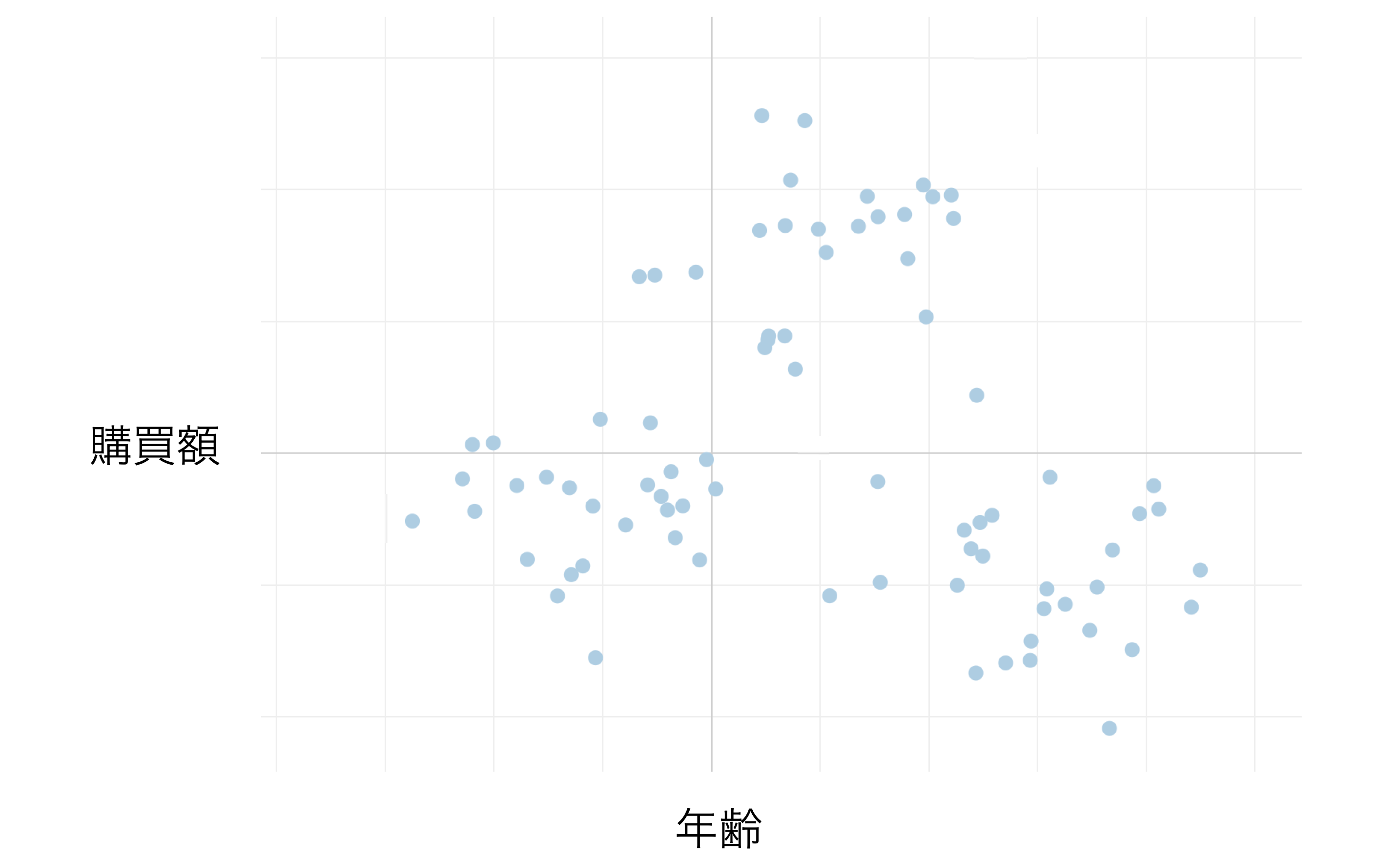
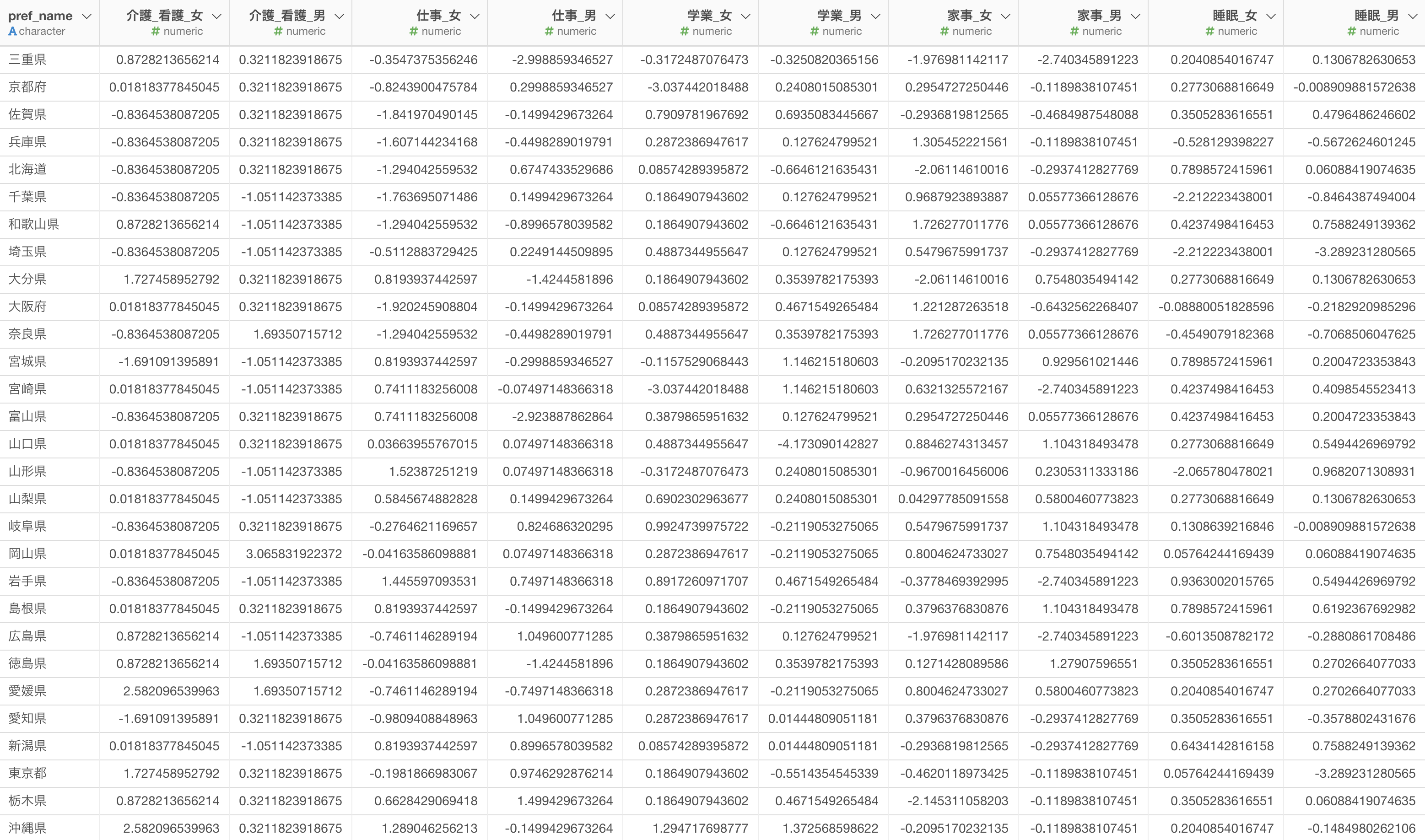
K-Meansクラスタリングを実行する際には、1行が1観測対象となっているデータを使う必要があります。
また、クラスタリングする元となる変数のデータ型は数値型になります。
サンプルデータ
今回使用するのは「Web会議サービスの顧客満足度調査データ」です。
このデータは、1行が1回答者を表し、サービスの使いやすさ、機能の豊富さ、品質、デザインなど10項目の評価が含まれています。
K-Meansクラスタリングを実行する
アナリティクスビューを開き、タイプに「K-Means クラスタリング」を選択します。
変数の列をクリックして、K-Menasに使用する列を選択します。シフトキーを押すことで、複数の列を一気に選択できます。
列の指定をした後に実行することで、K-Meansクラスタリングの結果が表示されます。
クラスターの数はデフォルトでは3となっています。
エルボーカーブで最適クラスター数を判断
最適なクラスター数のセクションでは、最適なクラスター数を決めるためのエルボーカーブが自動生成されます。
ガイド付きアナリティクスでは、「急減から緩やかになる境目(ひじ)」が最適なクラスター数の目安であることが説明されています。
今回の場合は、ばらつきの減少度の結果によりクラスター数は4つが適正であると考えられるため、クラスター数を4に変更します。

クラスターの数は設定から変更できるようになっています。今回はクラスターの数を「4」に変更して適用します。
クラスター数を4に変更してK-Means クラスタリングを実行することができました。
結果の解釈
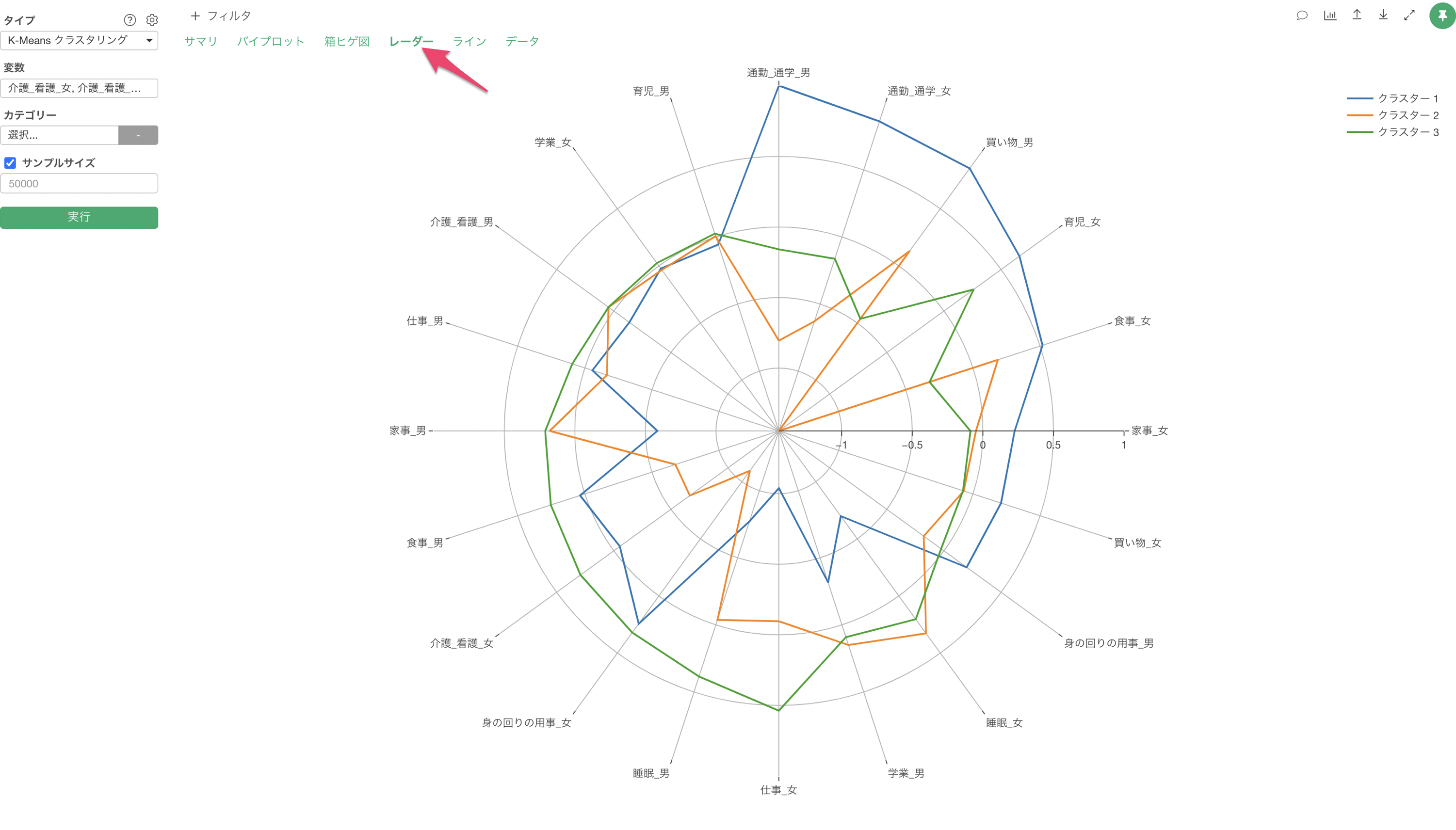
レーダー
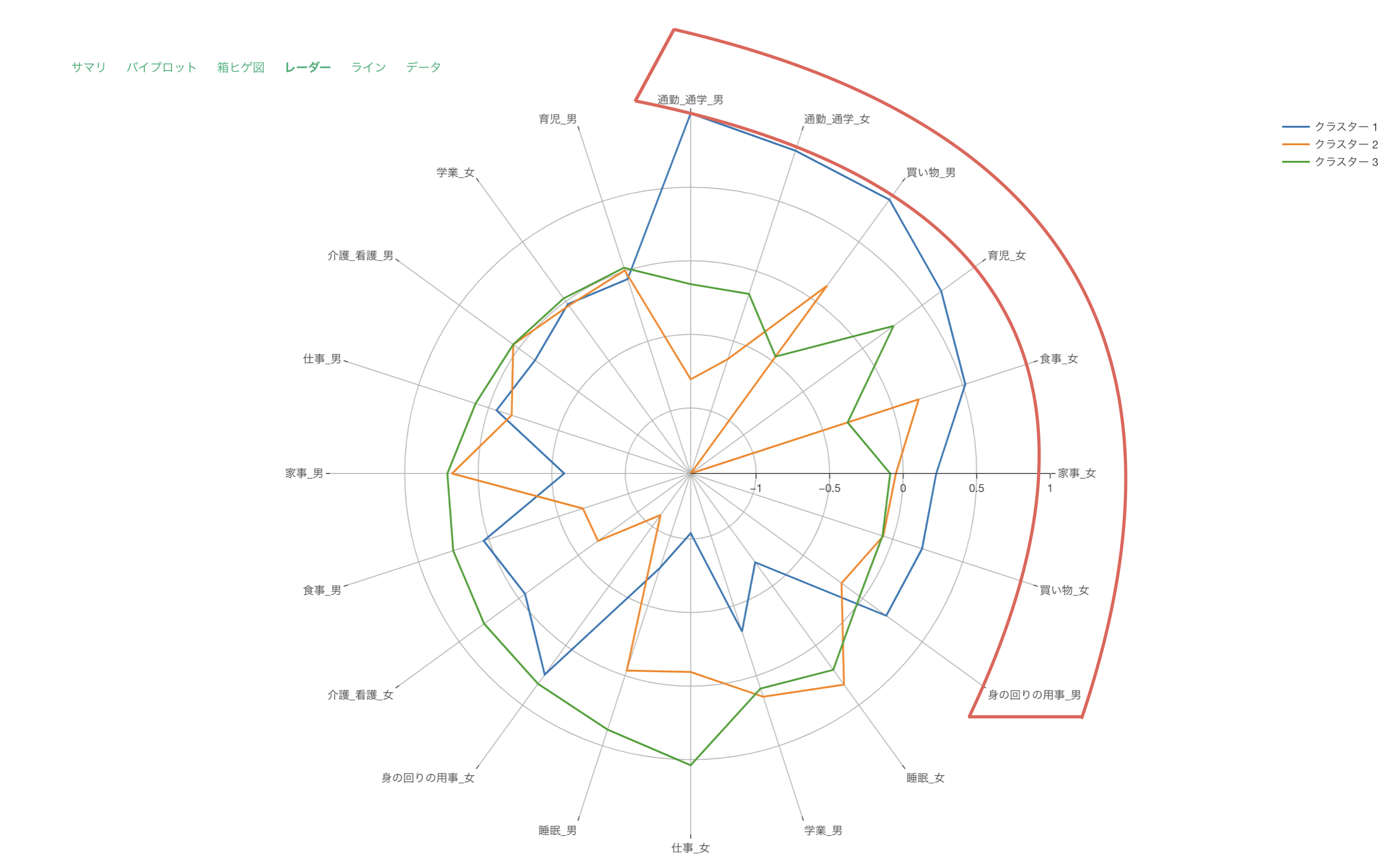
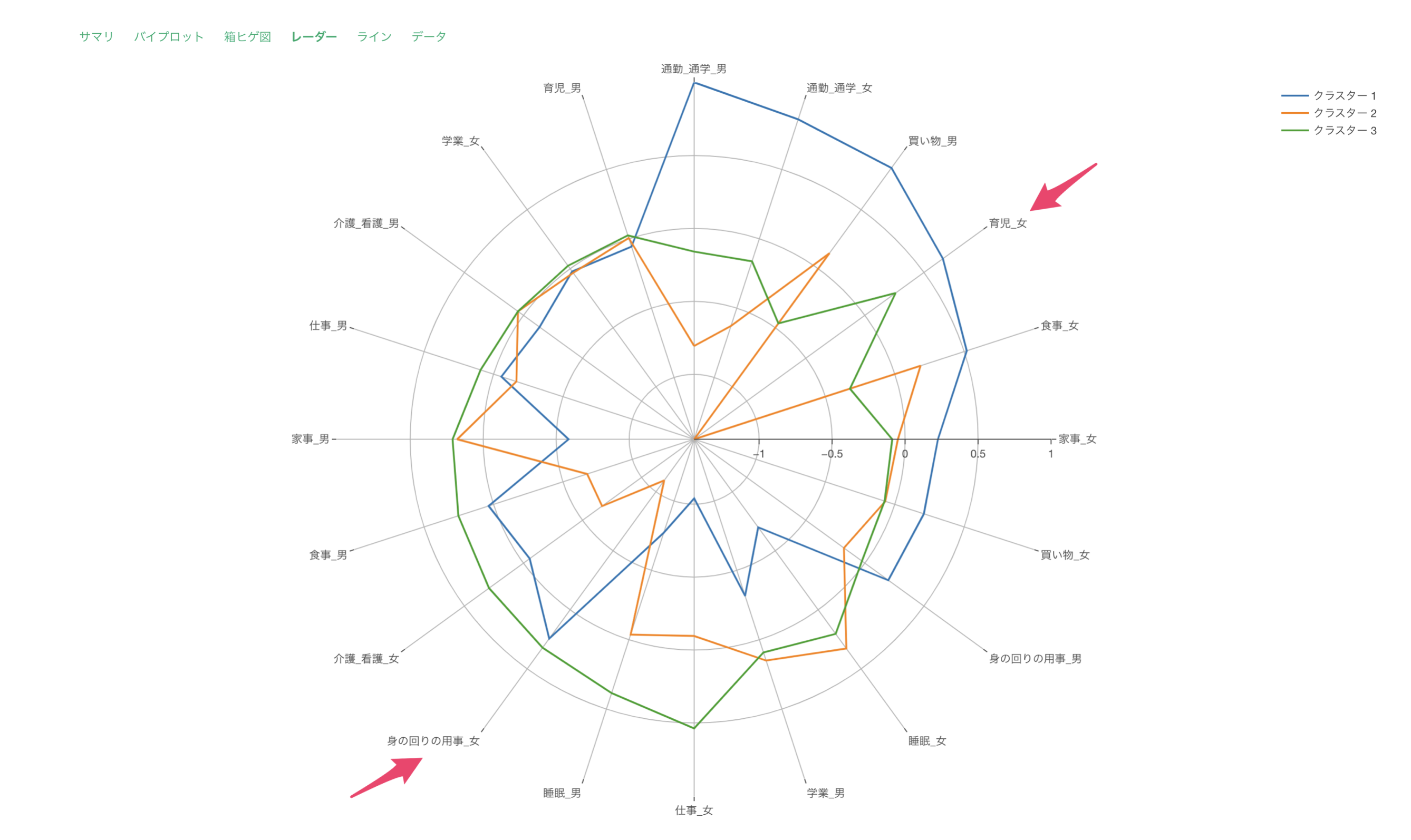
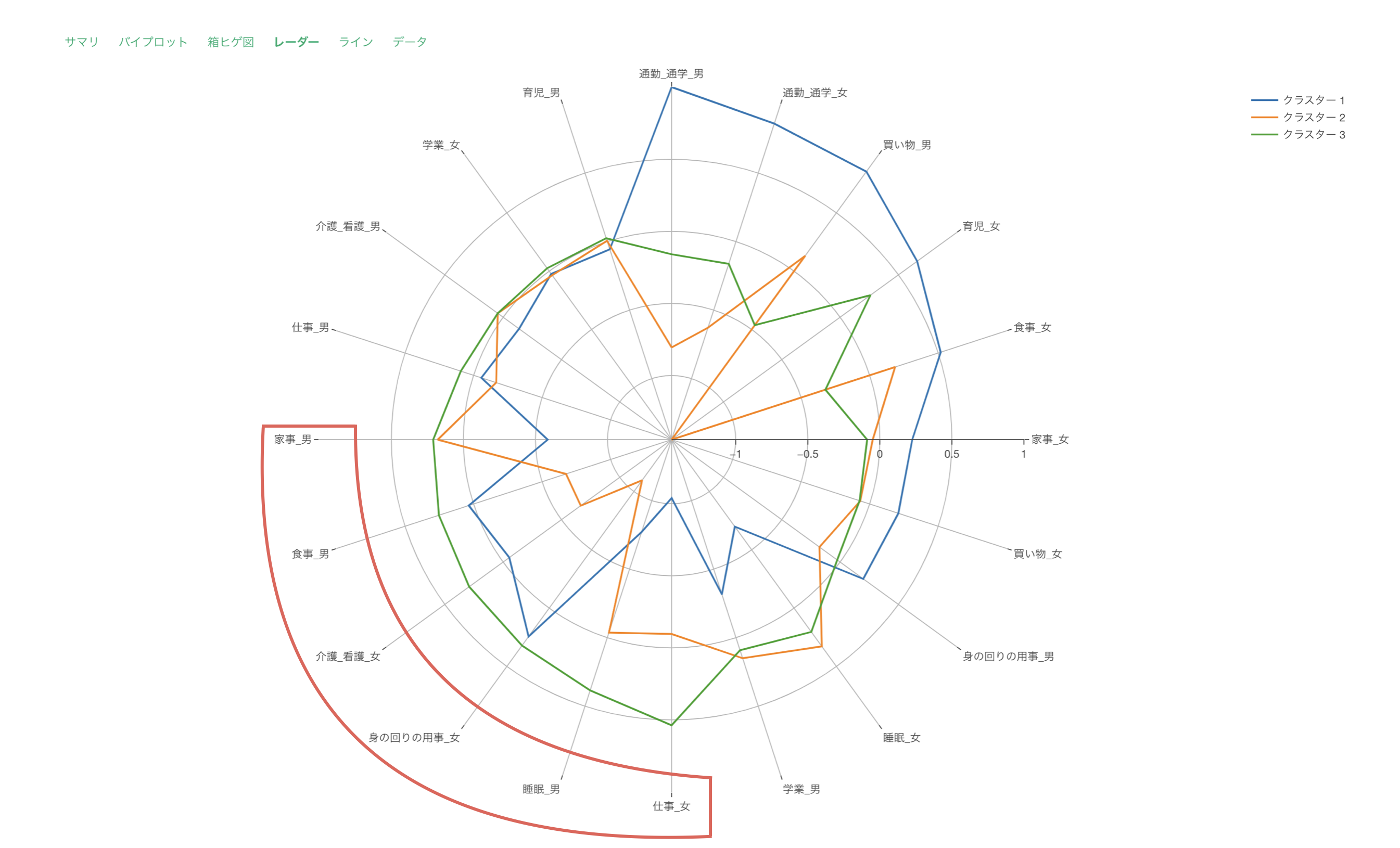
レーダーチャートによる可視化では、各クラスターでの変数を標準化した値を可視化しています。
このチャートで、クラスター3は全体的に高評価、クラスター1は全体的に低評価であることが分かります。
クラスター2は「サービスの機能の豊富さ」や「サービスの使いやすさ」などのサービスに関連するスコアが高く、クラスター3は「サポートの品質」や「サポートの応対速度」といったサポート関連のスコアが高いことがわかります。
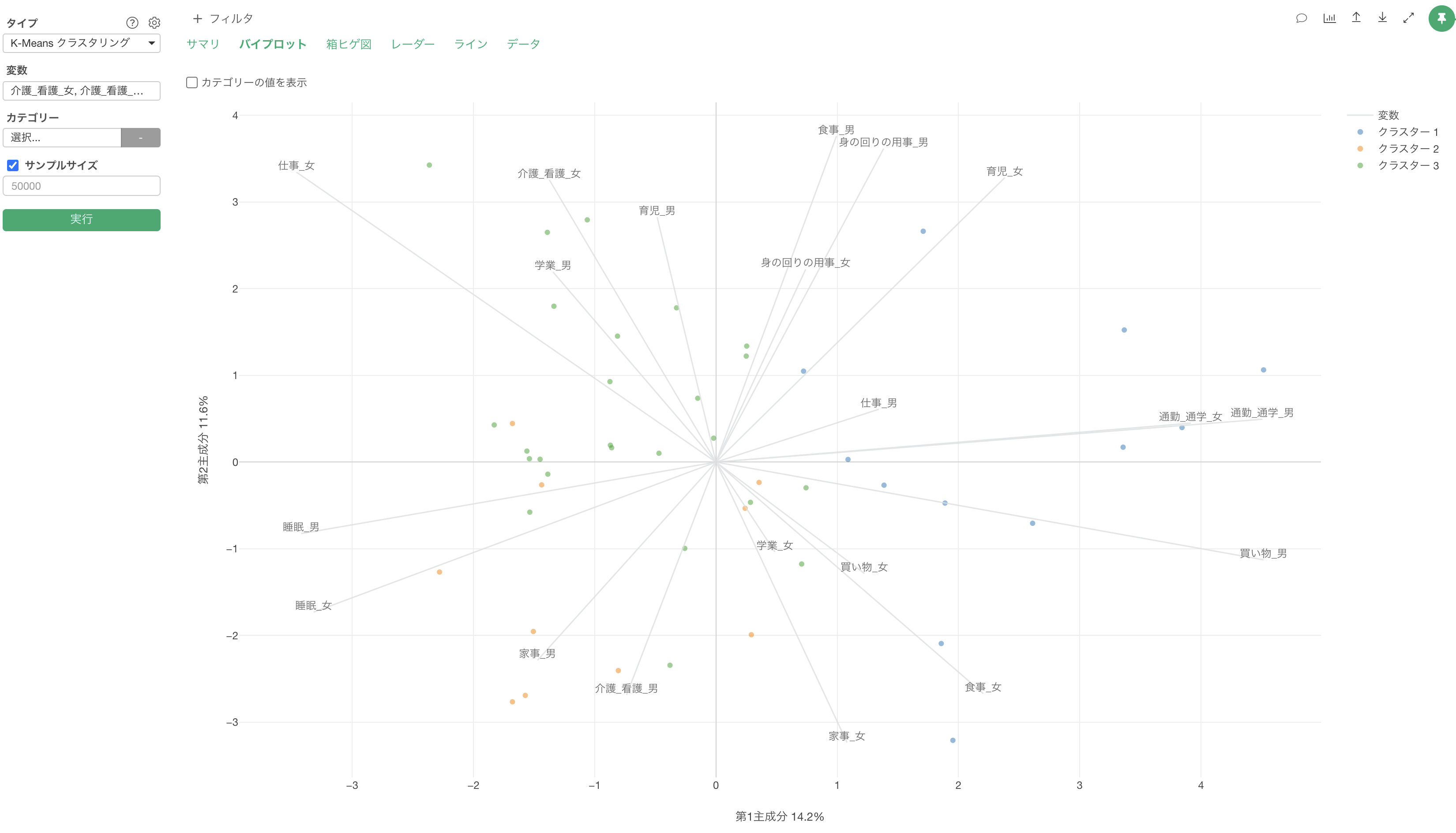
散布図による可視化(バイプロット)
散布図による可視化のセクションでは、それぞれのクラスター(グループ)ごとにどういった特徴があるのかを散布図上で確認できます。
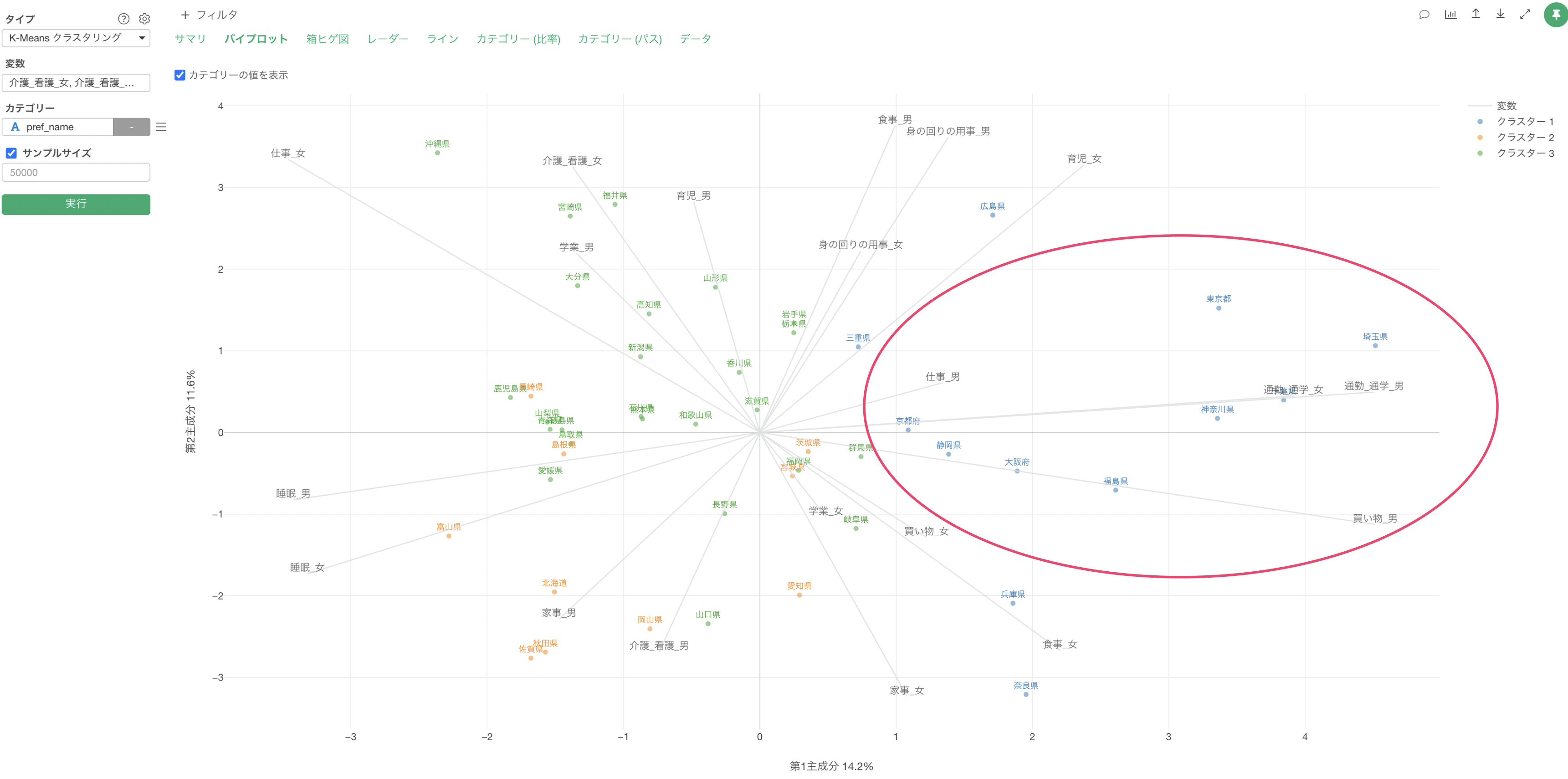
なお、この散布図による可視化で表示されている情報は、Exploratoryのアナリティクスのタイプの1つとしてサポートをしている「主成分分析」の結果となり、主成分分析の詳細はこちらから確認いただけます。
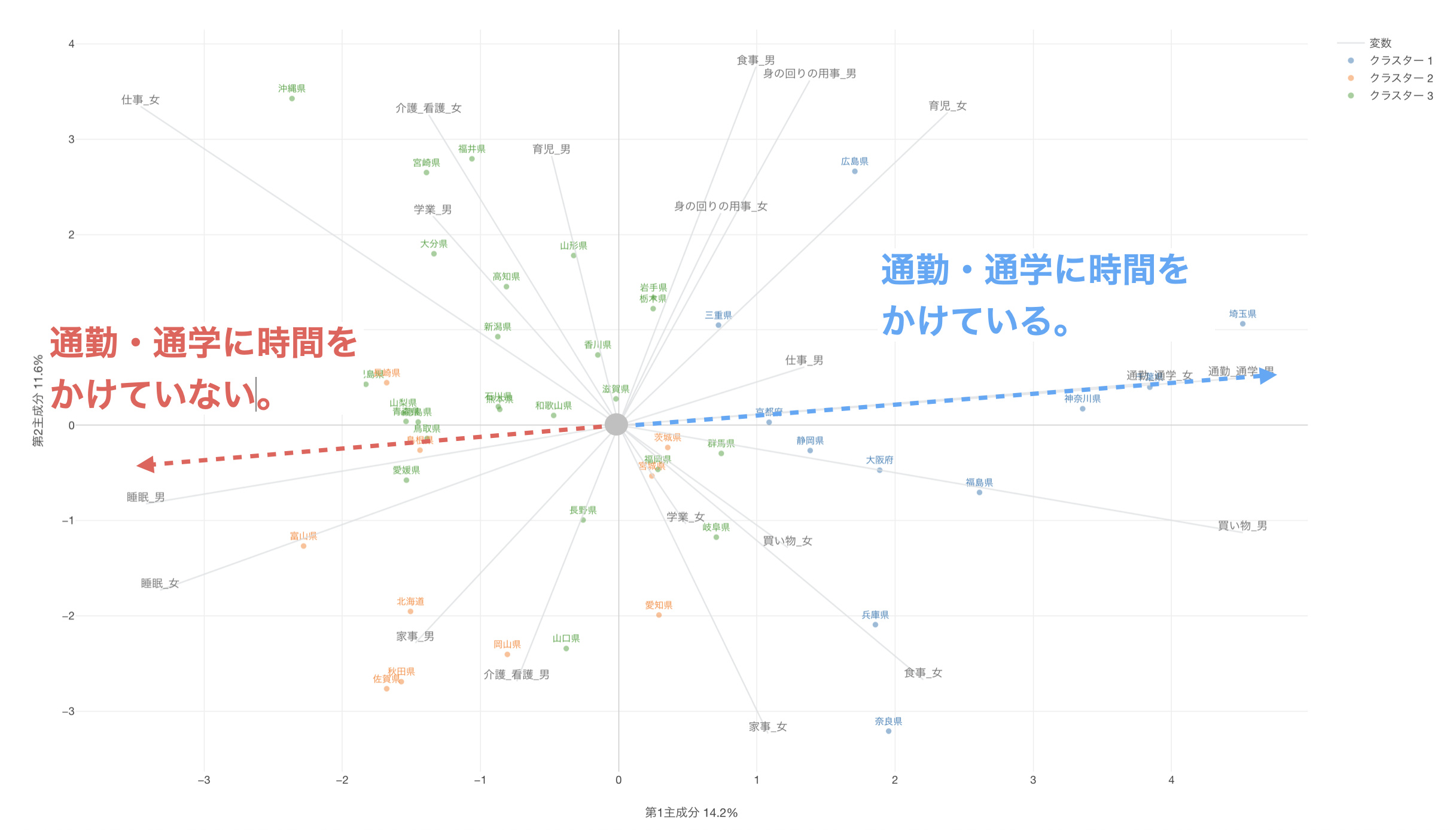
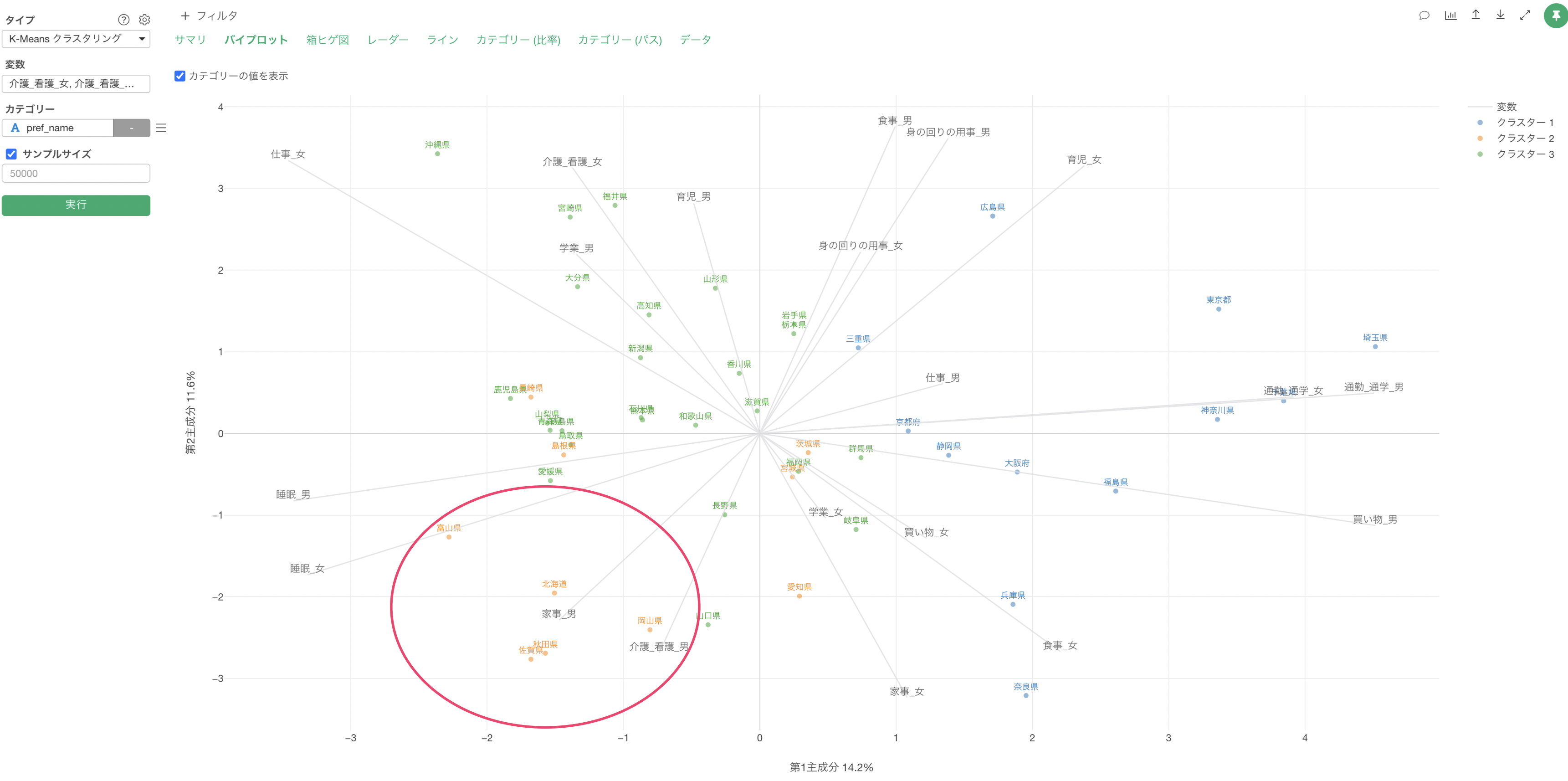
軸線が伸びている方向にある点(今回の場合は回答者)は、それらのスコアが高いことを表し、軸線の反対側にある点はそれらのスコアが低いことを表します。
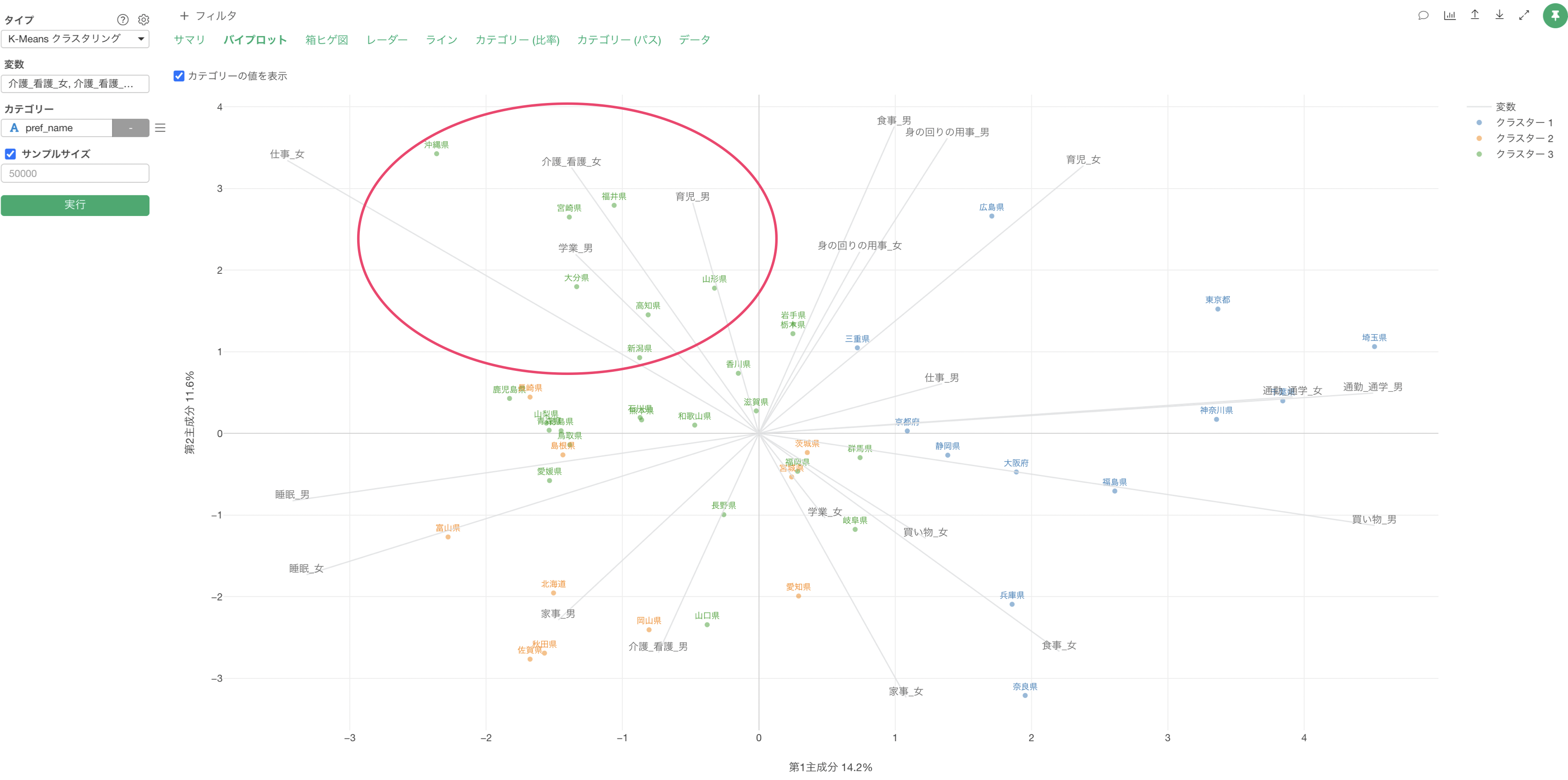
また、変数の線が同じ方向に向いている場合は、それらの変数で相関関係があると判断できます。
AI サマリを使って分析結果を要約
v13で新しく追加されたAIサマリ機能では、クラスタリング結果を自動的に要約してくれます。
使い方は驚くほど簡単で、K-Meansクラスタリングを実行した後に「AIサマリ」のボタンを押すだけです。
これによって各クラスター(グループ)のクラスター名と特徴をまとめた情報が出力されます。
今回のクラスタリングでは、以下のようなグループに分類されていることを要約してくれています。
各クラスターの特徴
- クラスター1: 低評価の価格重視グループ
- クラスター2: バランス型グループ
- クラスター3: 高評価グループ
- クラスター4: サポート重視グループ
このAIサマリを見るだけで、それぞれの分けられたグループにはどういった特徴を持っているのかをAIが判断して教えてくれるために、誰でも簡単にK-Means クラスタリングを使えるようになります。
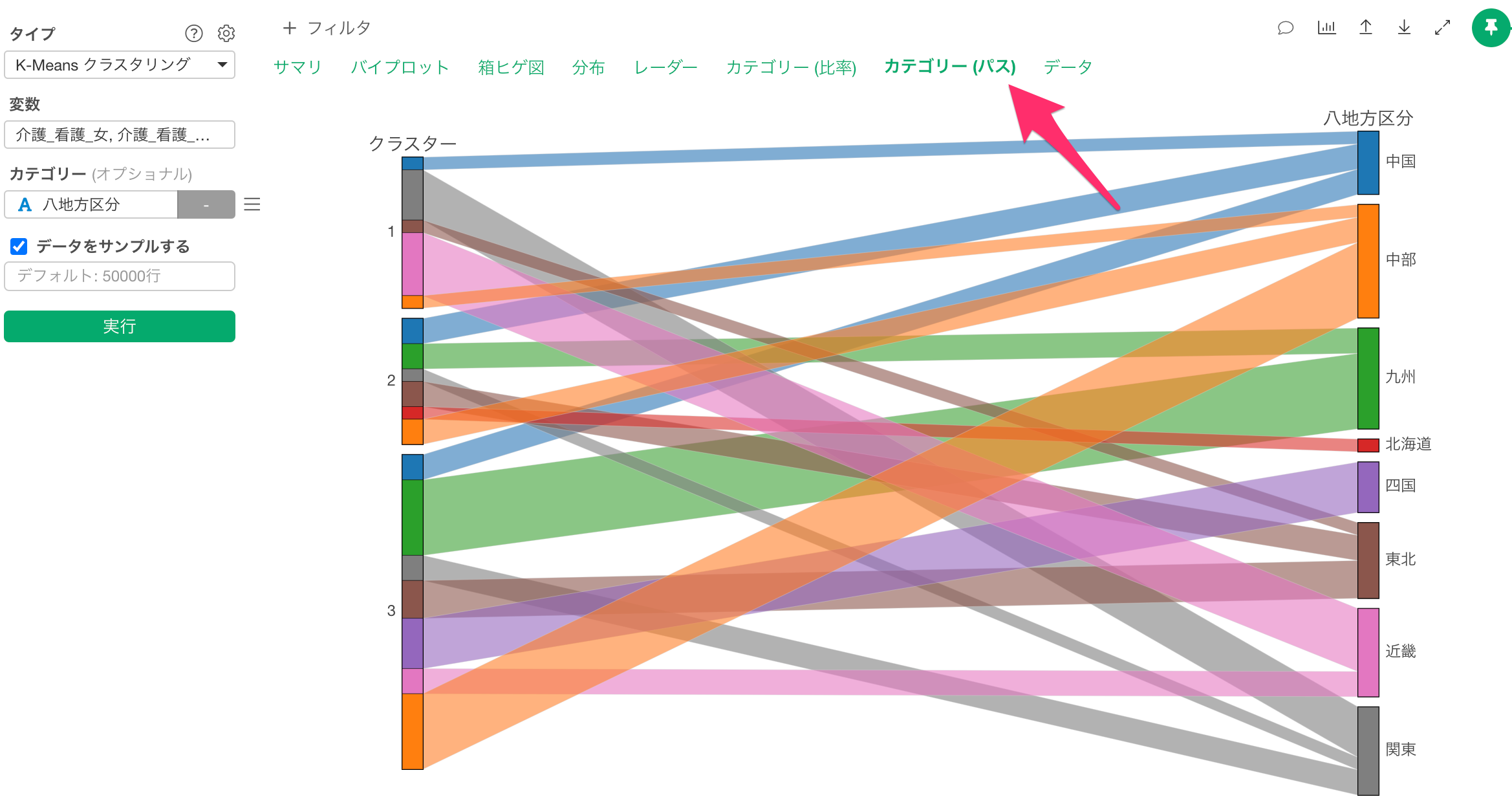
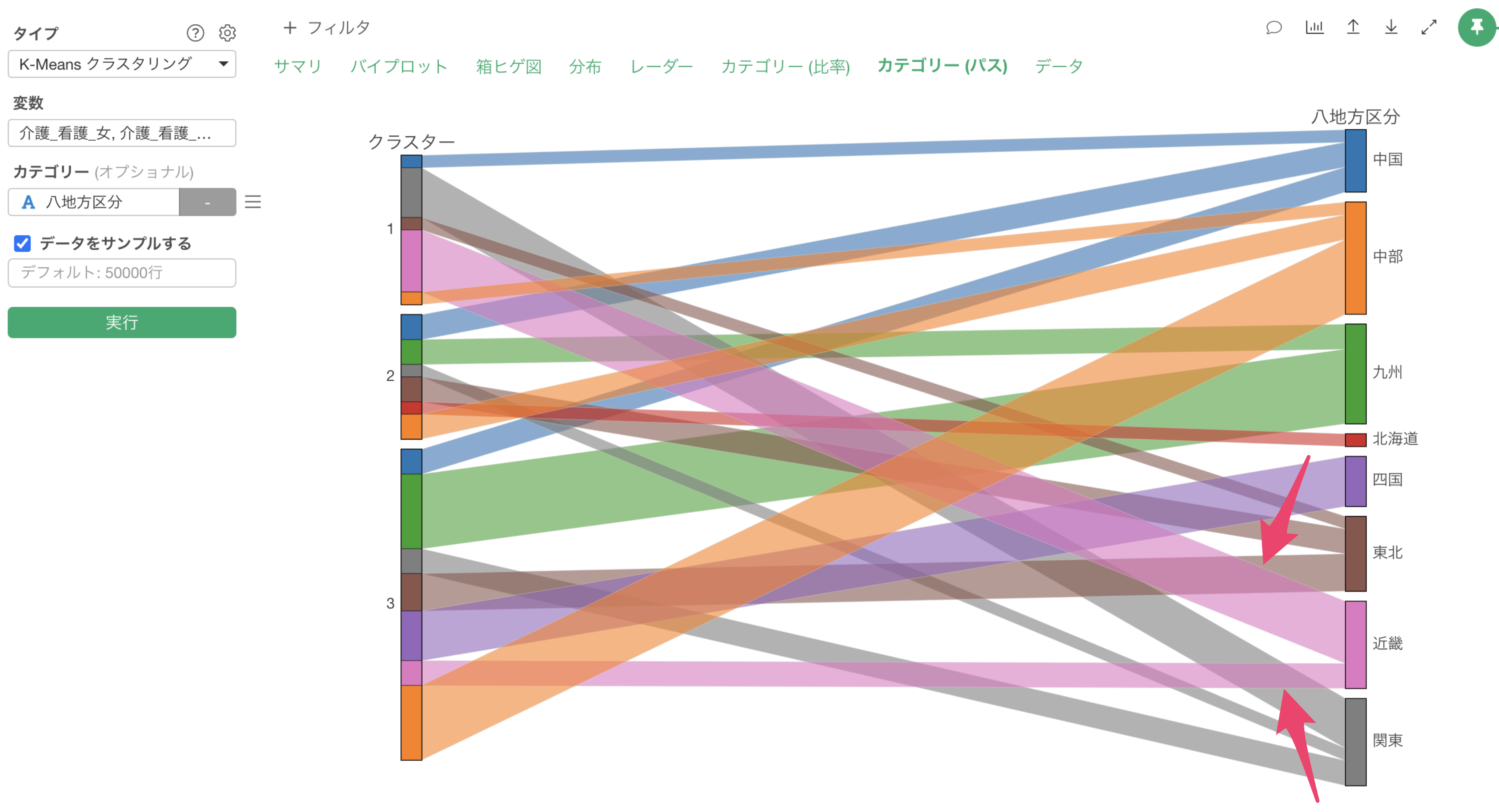
クラスターとカテゴリーの関係性を見る
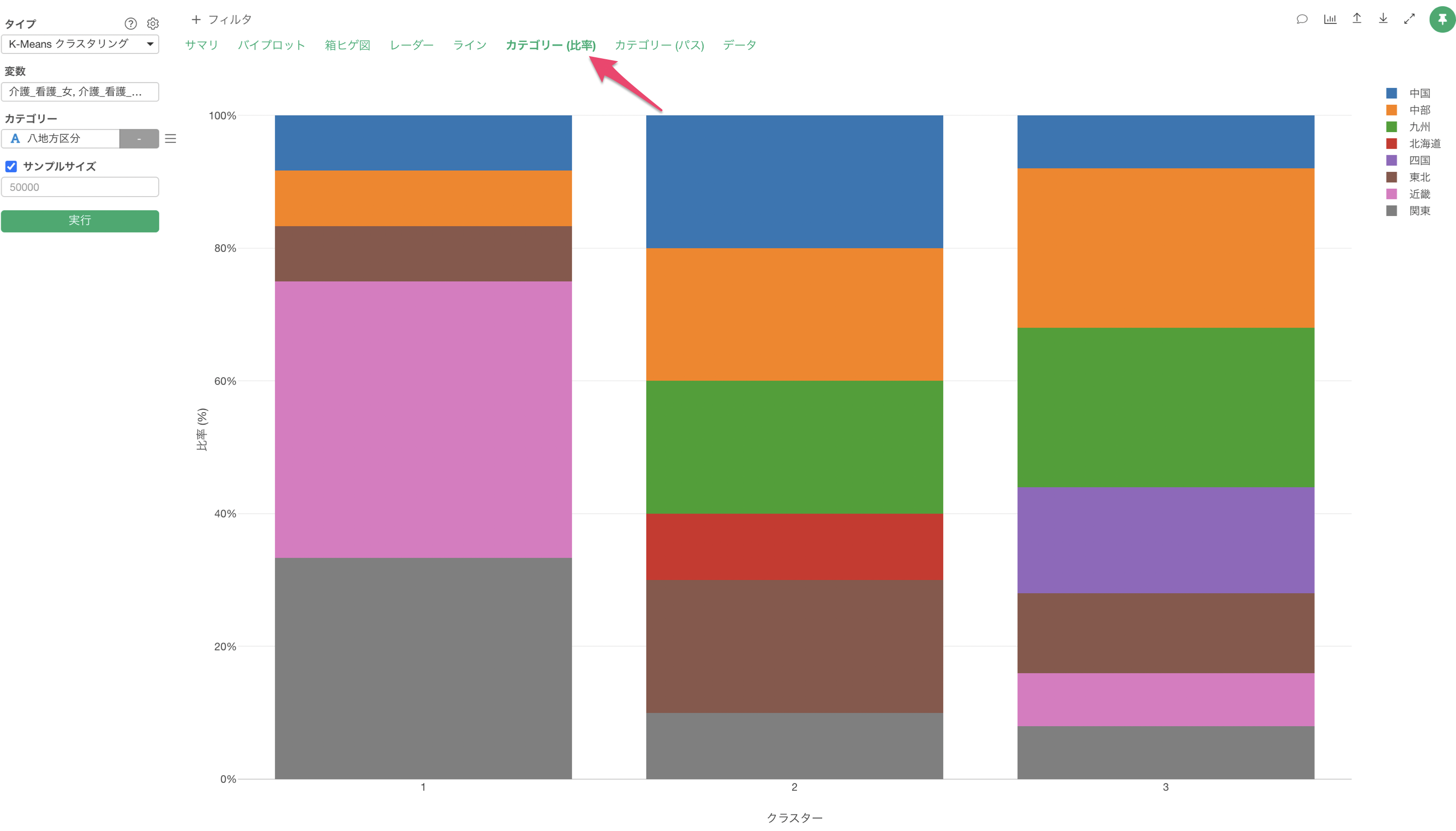
データの中に「NPSカテゴリ」の列があり、どのクラスターでプロモーター(推奨者)やでトラクター(非推奨者)が多いのかを知りたいとします。
K-Measnクラスタリングのカテゴリーに「NPSカテゴリ」の列を割り当てて実行します。
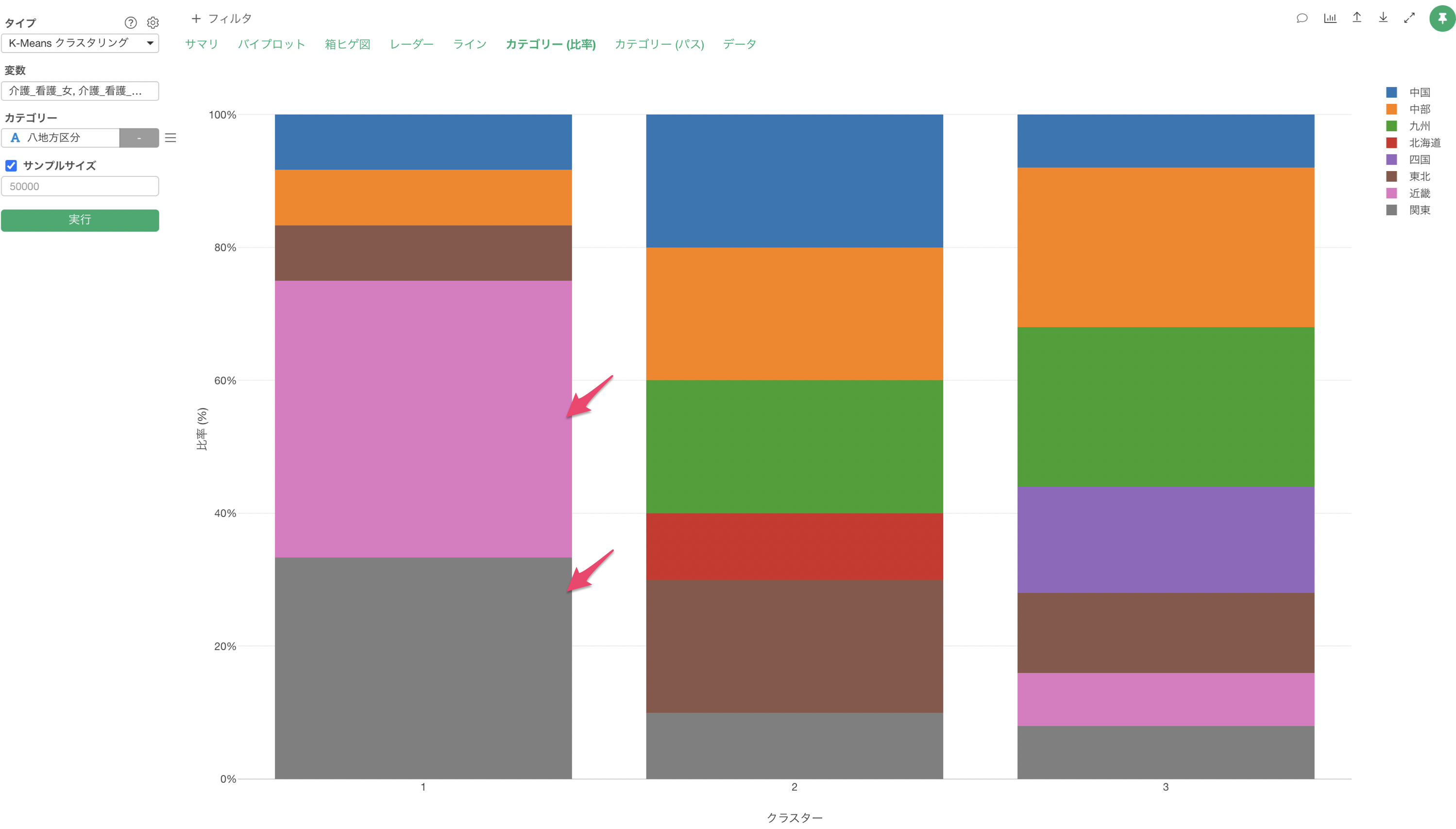
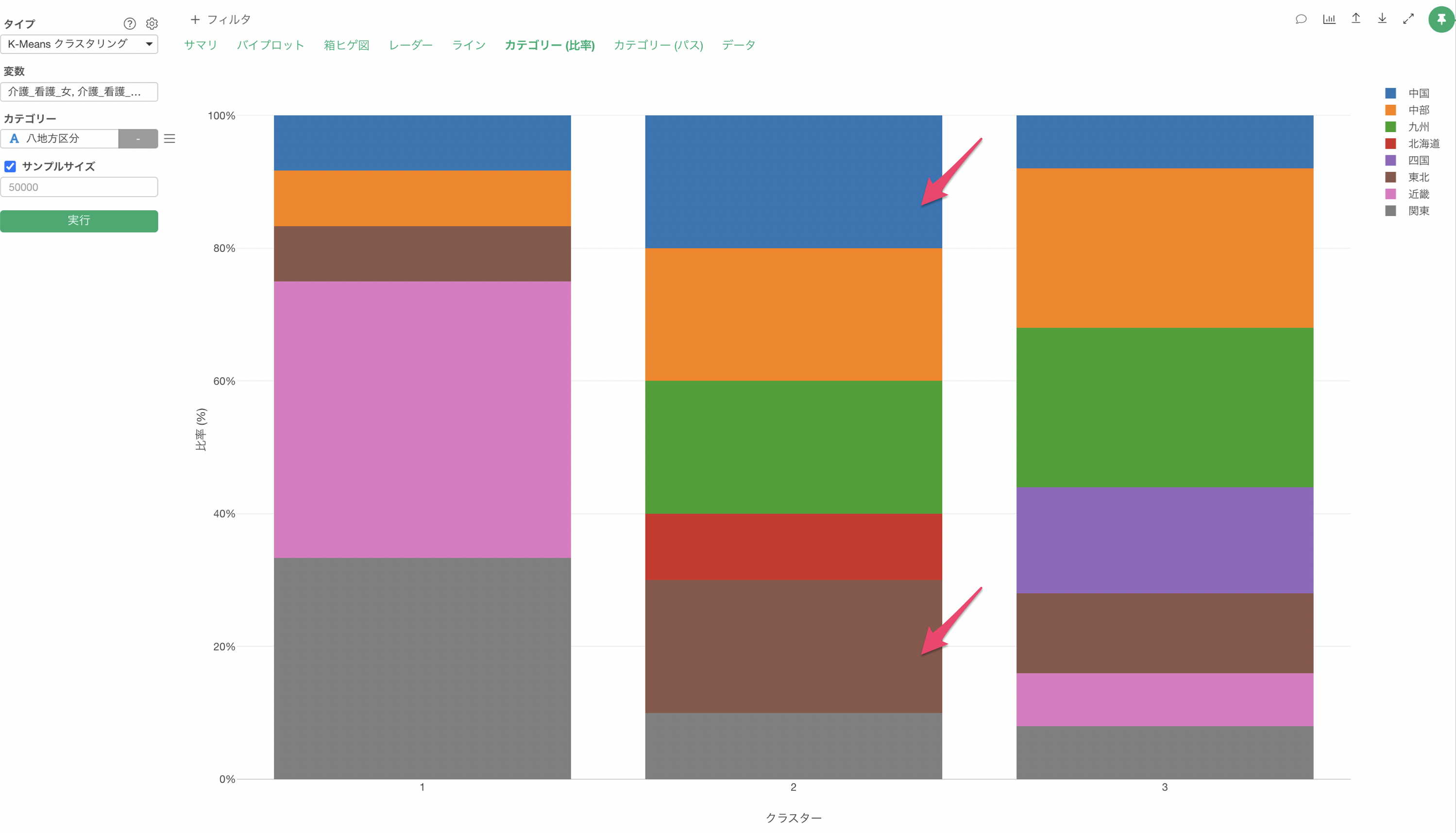
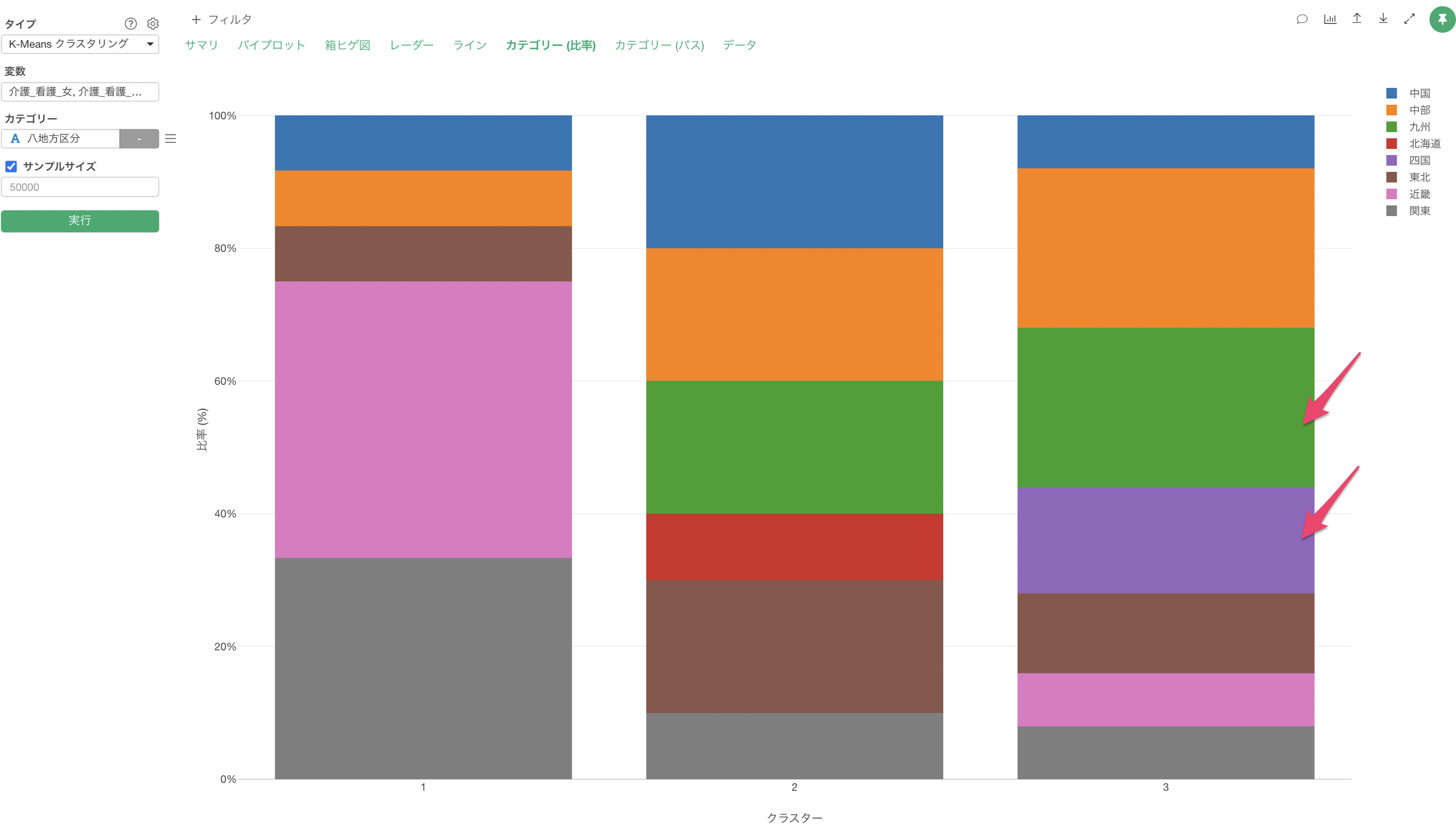
カテゴリー列を割り当てることで、「カテゴリーとの関係」のセクションが追加され、各クラスターで割り当てたカテゴリーの比率を確認することができます。
クラスター1は低評価の価格重視のクラスターでしたが、デトラクターーが多く集まっていることが確認できます。
クラスター3は高評価のクラスターでしたが、プロモーターの比率が高いことが確認できます。
クラスタリングしたデータをエクスポートする
データのセクションにあるテーブルでは、K-Meansクラスタリングに使用されているデータとクラスター番号を確認できます。
このデータをデータフレームとして保存したい場合は、エクスポートボタンから「チャート・データを新規データフレームとして保存」を実行します。
クラスタリングで使用したデータが新しくデータフレームとして作成されました。
参考資料
K-Meansクラスタリングに関する参考資料は下記をご覧ください。
K-Meansクラスタリングに関するよくある質問
Q: K-Meansクラスタリングを実行すると「Centers should be less than distinct data points.」というエラーが表示される。
K-Meansクラスタリングを実行したときに、Centers should be less than distinct data points.というエラーが表示され、K-Meansクラスタリングの結果が返らないことがあります。
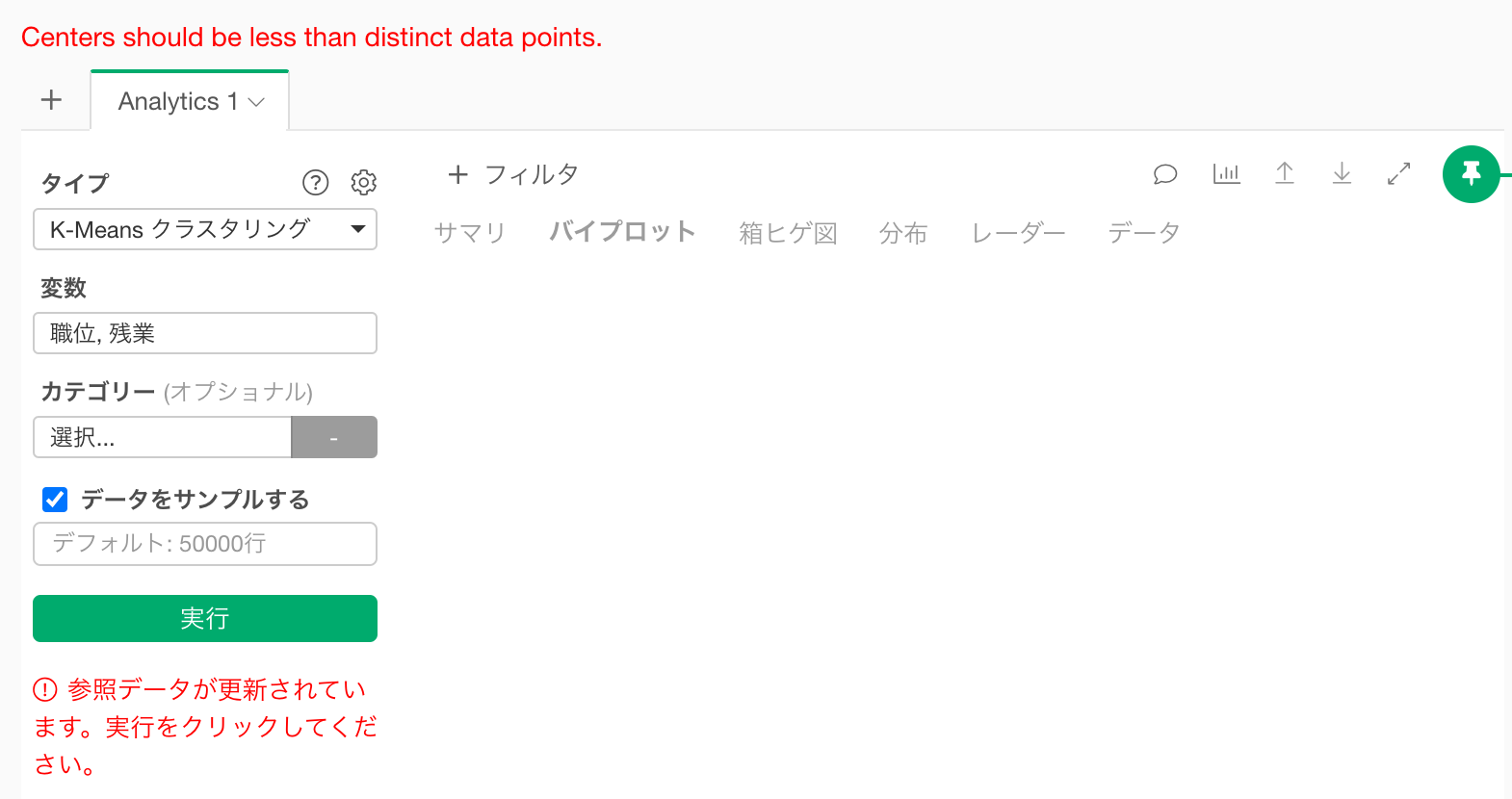
このエラーは、クラスタリングに利用している各行の列の値の組み合わせの数が、設定しているクラスター数(デフォルトは3)より少ない場合に生じます。
そのため、クラスターの数を、前述した値の組み合わせの数より少なくなるように、減らすことで、エラーを回避することが可能です。
Q: K-Meansクラスタリングにおけるランダムシードとはどのような設定ですか?
K-Meansクラスタリングは、クラスタリングを始めるときに、ランダムにクスラターの中心を決めるところから処理を始め、観察対象をクラスターに分けていきます。
ランダムシードはそのときの初期中心の位置を決めるための「番号」のようなものです。
Exploratoryでは、デフォルトで同じシードを利用しているため、データとデータの順番が同じ場合、毎回同じ結果を得られことに役立っています。
ただし、MacとWindows間では文字エンコードの違いにより、シードが同じ場合でも、割り当てられる、クラスター番号が異なるなど、わずかな差異が生じることもあります。
Q: K-Meansクラスタリングを実行した際、データの並び順によって結果にばらつきが生じます。結果のばらつきを減らすために、できることはありますか?
K-Meansクラスタリングは、クラスタリングを始めるときに、ランダムにクスラターの中心を決めるところから処理を始め、観察対象をクラスターに分けていきます。
そのため、データの並び順が変わることで、最初に設定されるランダムな中心が変わってしまい、得られる結果が変わることは想定されることになります。
一方でデータの並び順による結果のばらつきを減らすためには、「試行回数」や「最大反復回数」、特に「試行回数」を増やすことが有効と言えます。
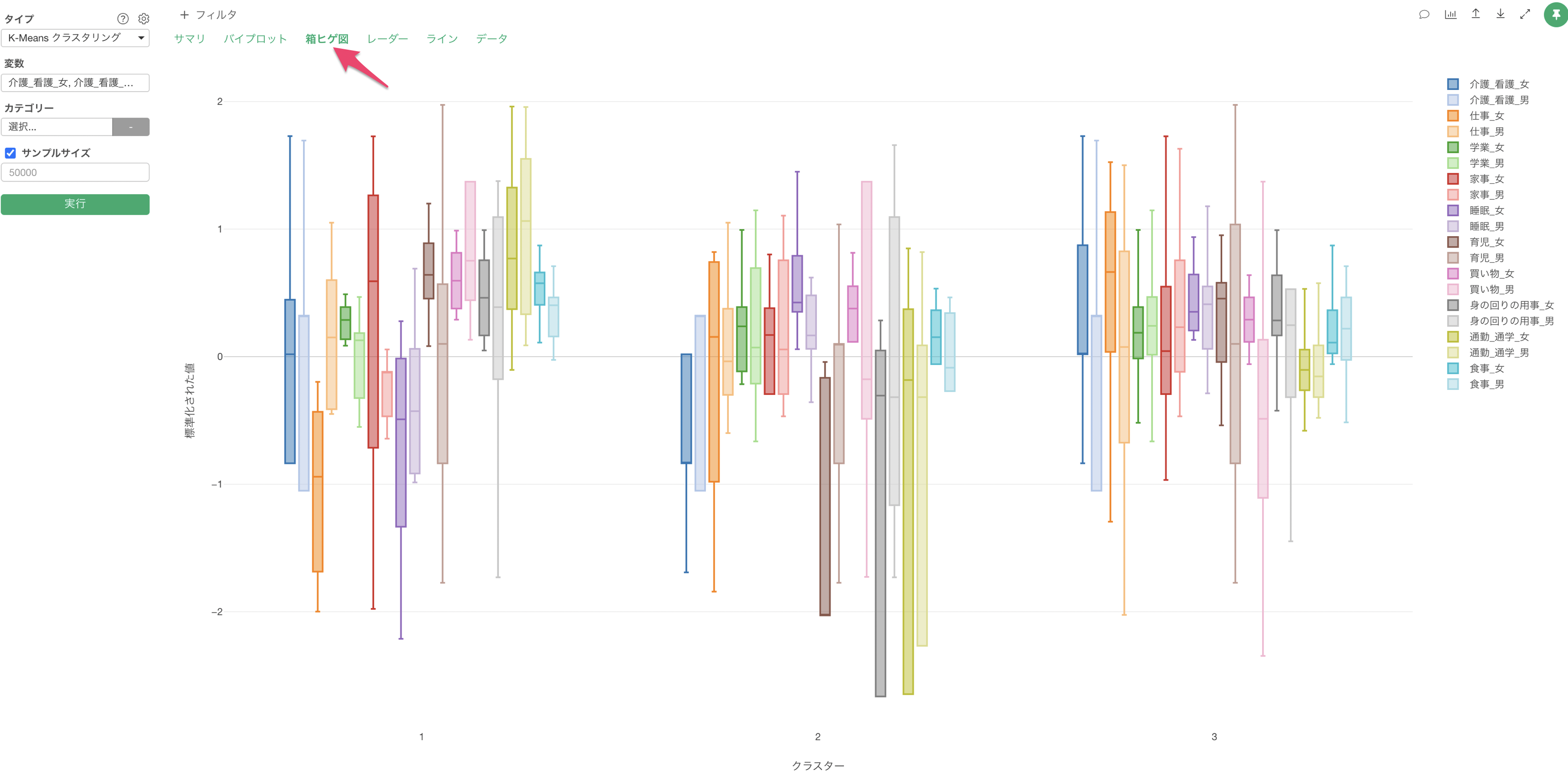
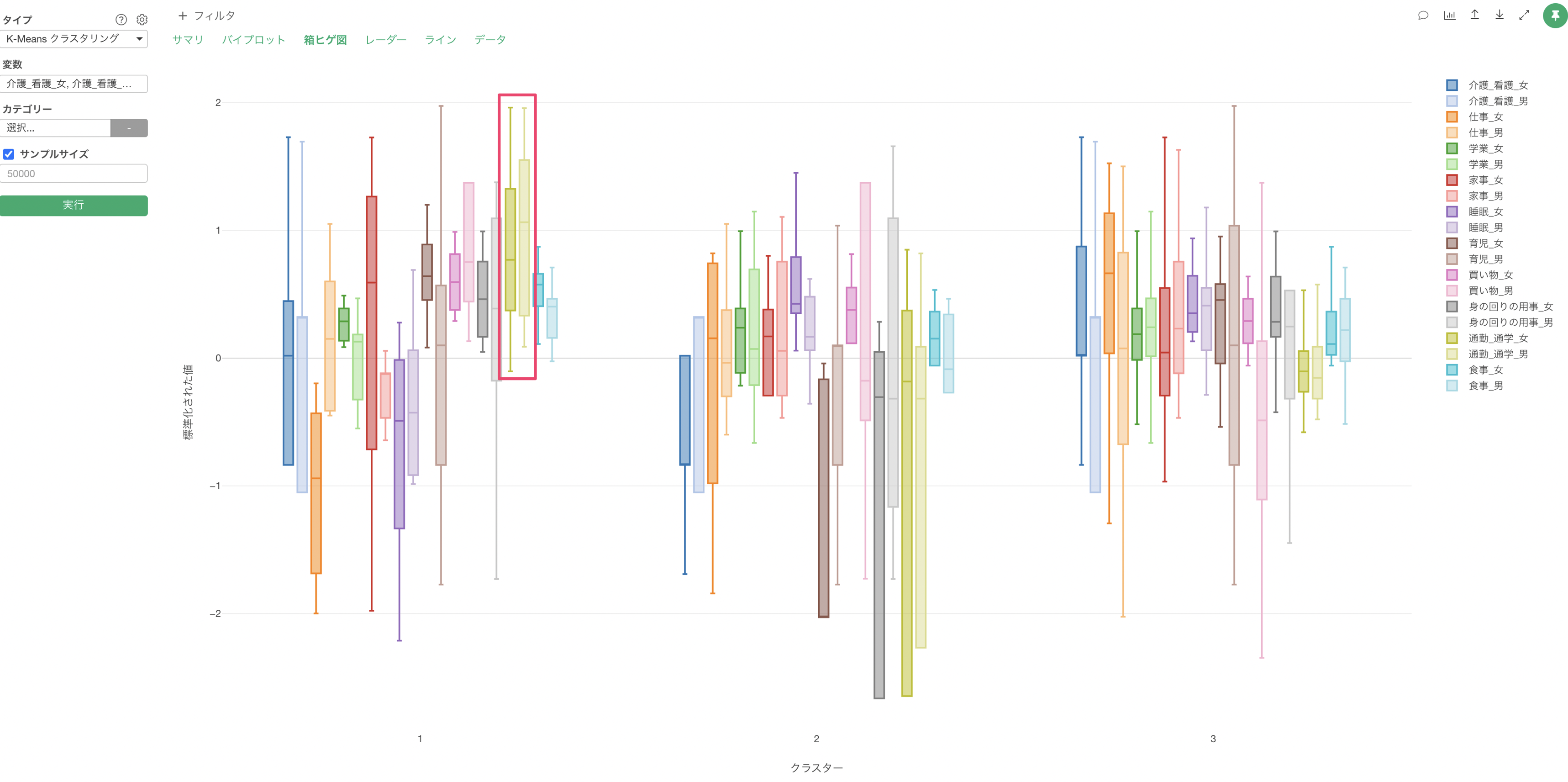
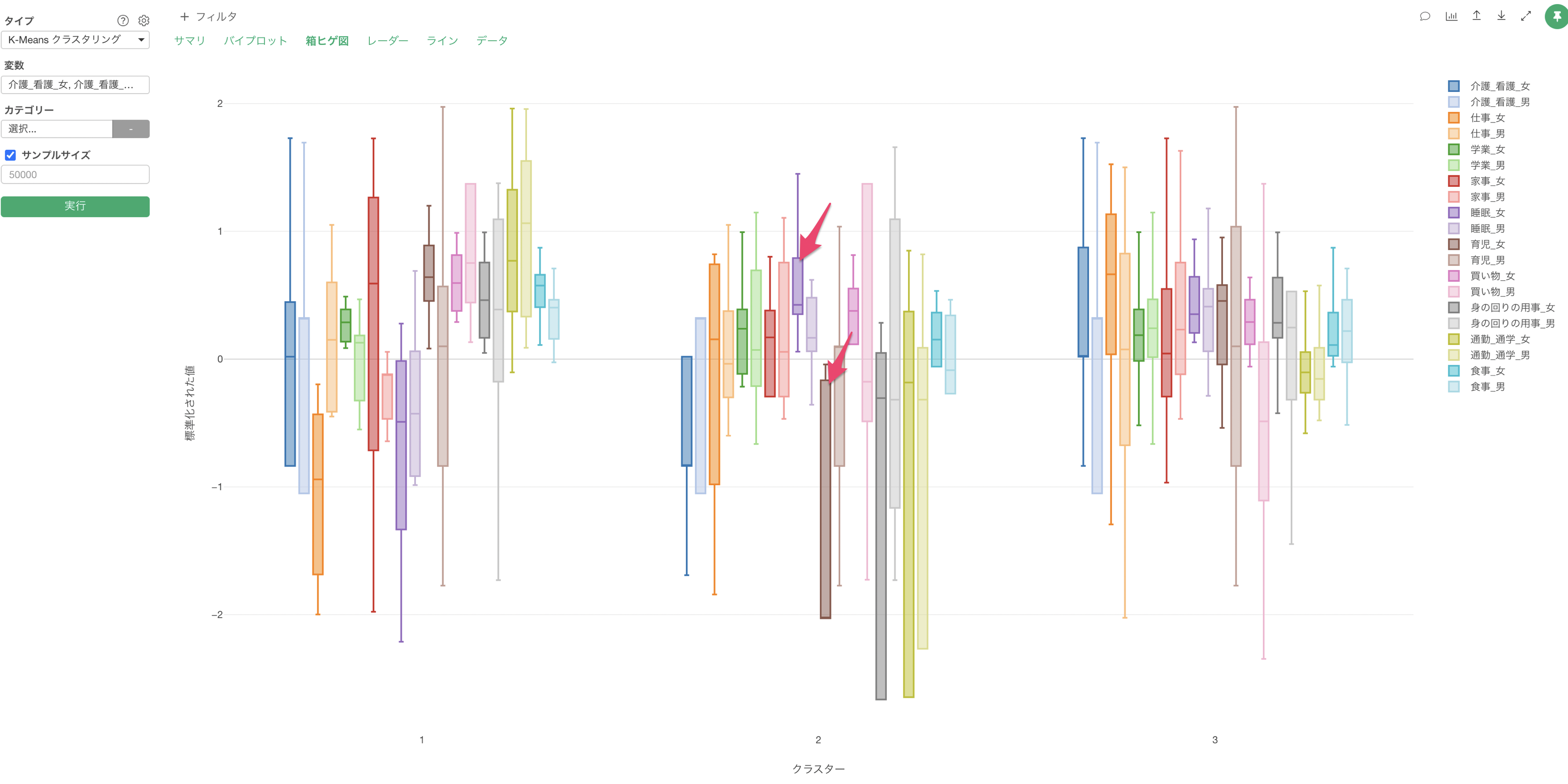
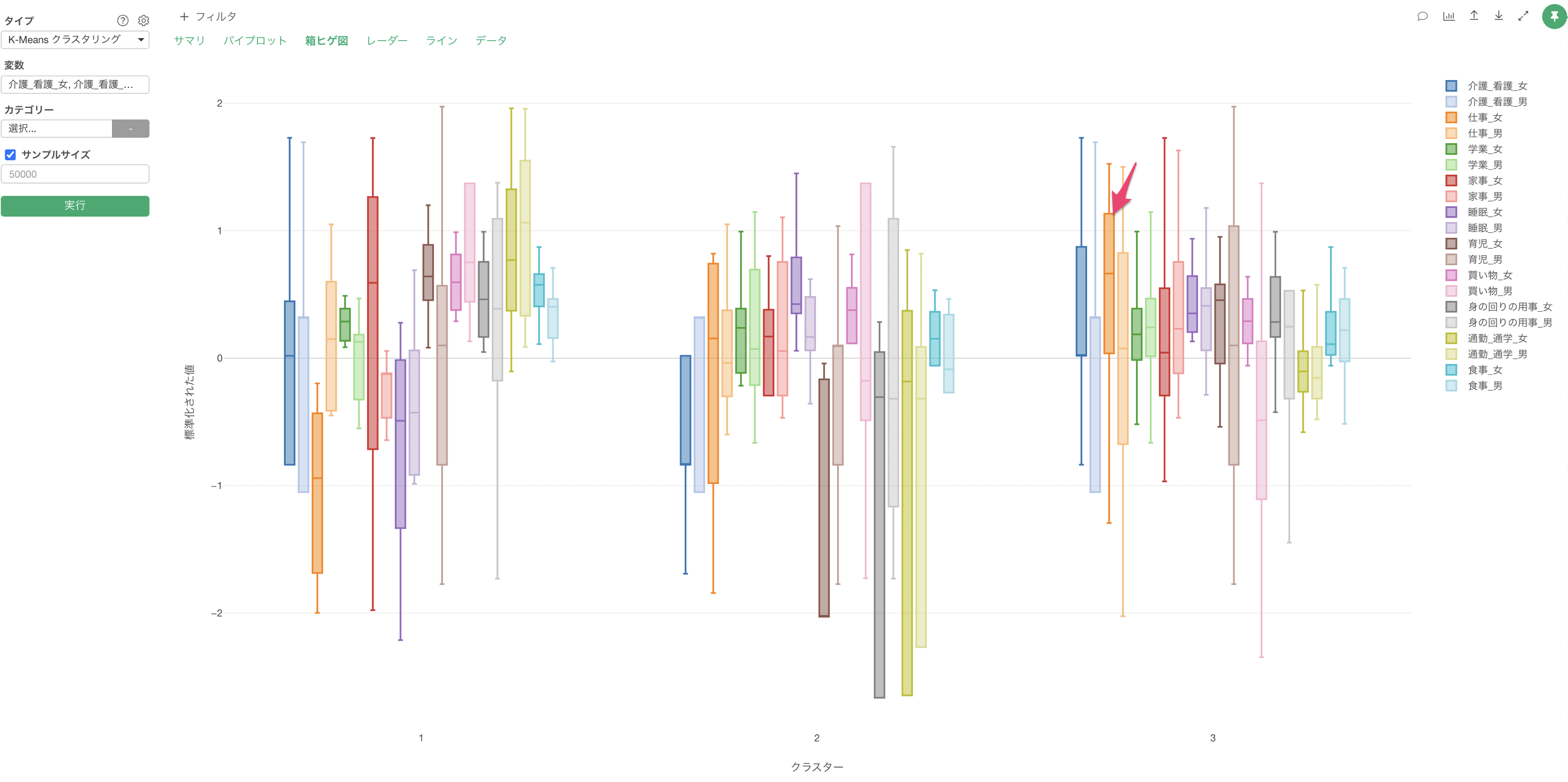
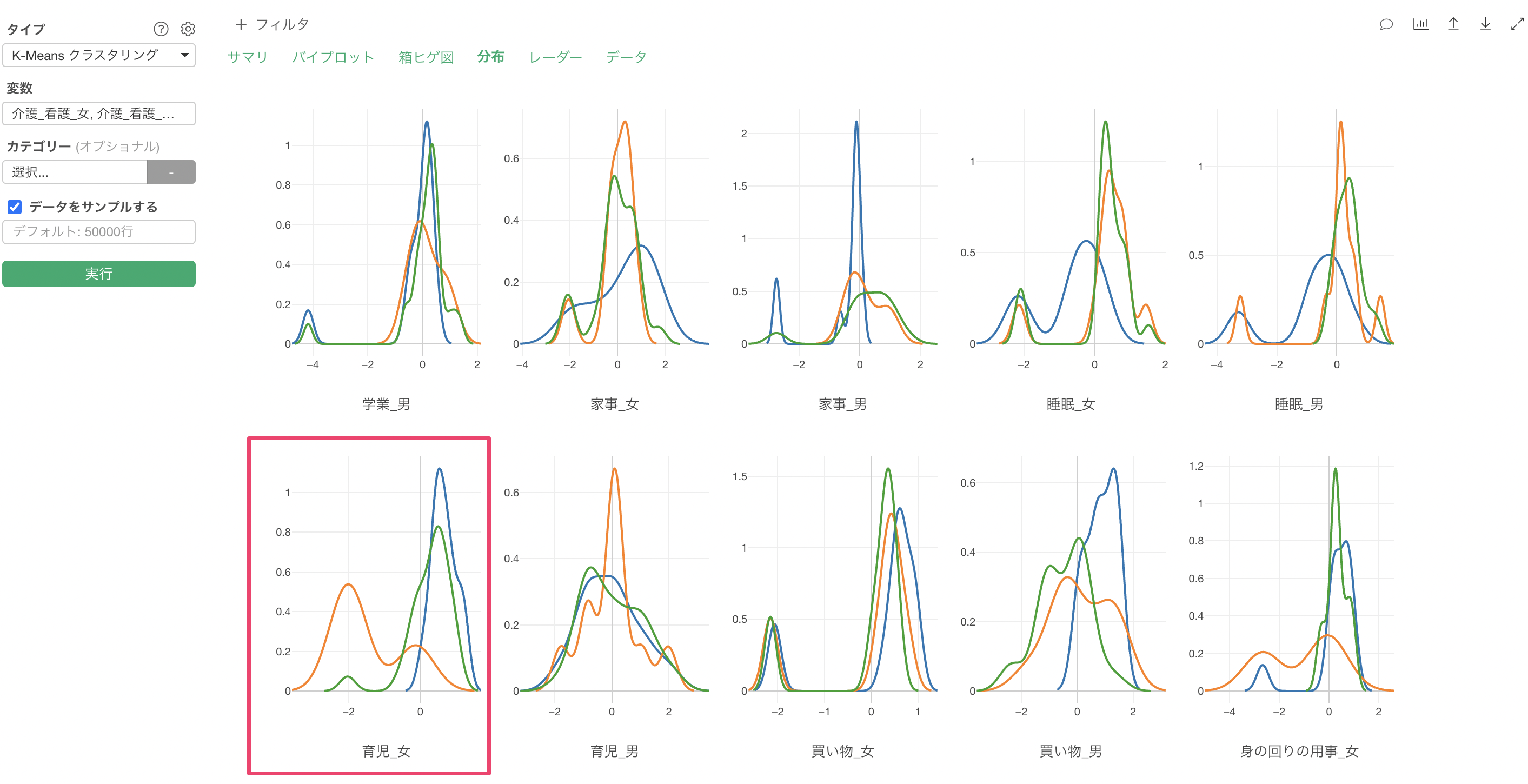
Q: K-Meansクラスタリングの「箱ヒゲ図」で「箱」や「ヒゲ」が描画されません
K-Meansクラスタリングの「箱ヒゲ図」のタブにて、「箱」や「ヒゲ」が上手く描画できないケースがあったりします。K-meansで使用している変数に「偏りがある」場合は、箱ヒゲ図が上手く描画できない原因の一つとなります。
詳細は、こちらのノートをご覧ください。
Q: サマリタブに表示されるクラスター内平方和とはなんでしょうか?
クラスター内平方和は各クラスターの中心地からのそれぞれのデータのずれの合計だと捉えていただければと思います。この値が小さければ小さいほどずれが少なくなり、K-Meansではこのクラスター内平方和を少なくするために、クラスターの中心となる点をずらしていくという手法となっています。
Q: クラスター間平方和とはなんでしょうか?
クラスター間平方和はクラスターの中心が、全データの中心からどれだけ離れているかを示す指標となり、各クラスターがどれだけ綺麗に分かれているかを測る相対的な指標となり、Between-Cluster Sum of Squares(BCSS)と呼ばれることがある指標です。
Q: 設定メニューに表示される「反復回数」や「試行回数」は何を表していますか?
K-Means クラスタリングでは最初にランダムにクラスターの中心点の位置を決め、観察対象をクラスターに分けることになります。
Exploratoryではシードがセットされているため、同じマシンで実行している限りは結果が変わることはありませんが、最初に決められたクラスターの中心点が変わることによって結果が変わってしまうことがあります。
そこで試行回数ではK-Meansクラスタリングがグループ分けをする処理を試行する回数、言い換えれば、クラスターの中心点の位置を決め、観察対象をクラスターに分ける処理を繰り返す回数を決められるようになっています。
なお、反復回数は1回の試行の中で、クラスターに分けるための処理の実行回数を表しています。
Q: 設定メニューに表示される「反復回数」や「試行回数」を減らすことでどのような効果を期待できますか?
一般的に試行回数や反復回数を増やすことで、ランダム性を減らすことができ、安定した結果が得られる可能性が高まることになります。
一方で試行回数や反復回数には答えがあるわけではないため、得られた結果(例: それぞれの設定を変更しても結果があまり変わらない)をもとに最適なな設定を判断していくことになります。
Q: サマリタブに表示される各変数の値はどういった値が表示されているのでしょうか?
サマリタブで表示される変数は全て標準化した値のクラスターごとの平均値となっています。色がついたバーはその値の大きさに応じてバーが長さが変わります。値がプラスであれば水色に、マイナスであれば赤色で表示されます。
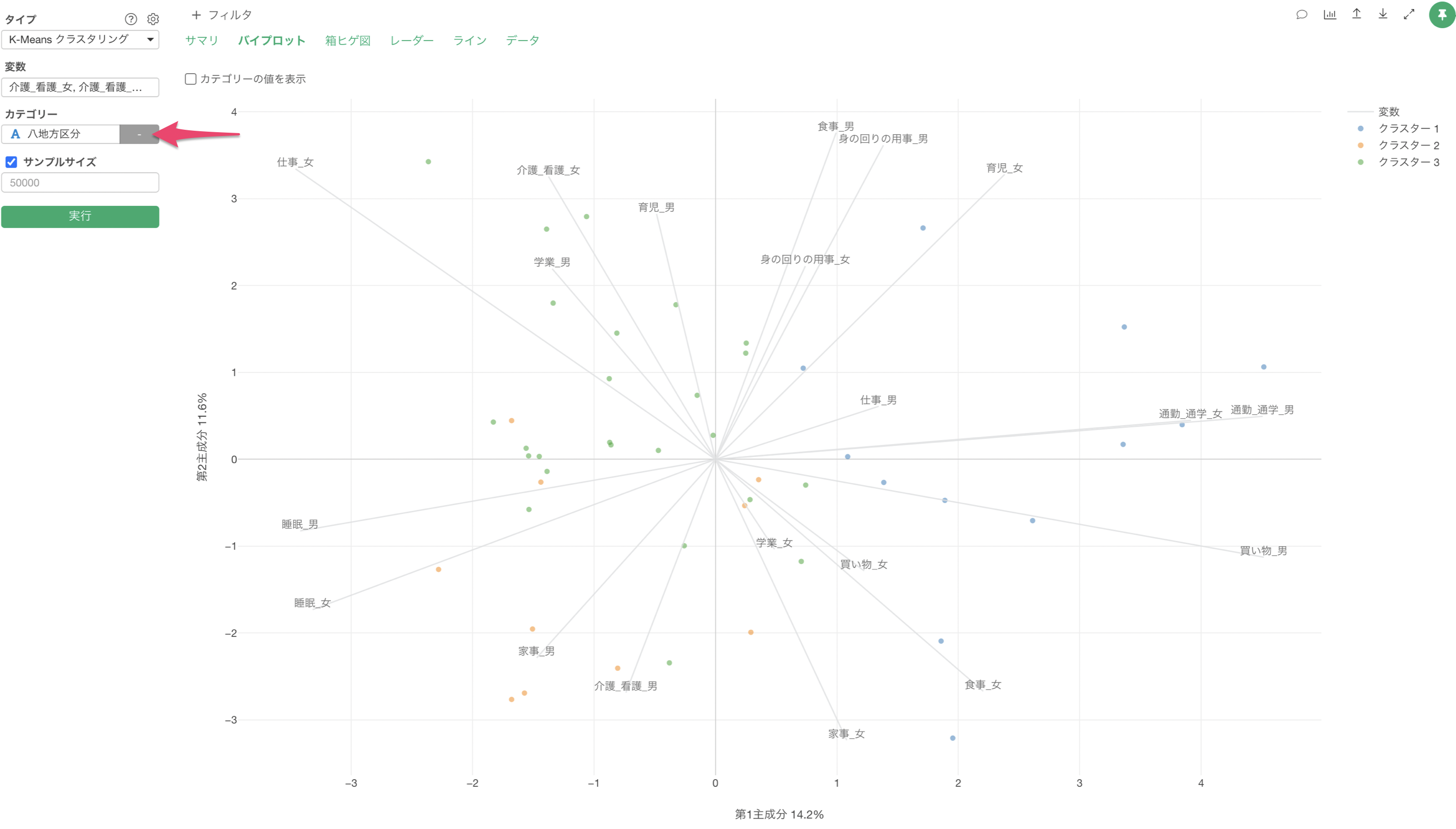
Q: バイプロットタブに表示されている第1主成分、第2主成分は何を表しているのでしょうか?
バイプロットでは次元削減のアルゴリズムである主成分分析(PCA)というものを使っており、複数の変数を2つの次元で表した時にどれだけの情報量(ばらつき)を表現できているかが第1主成分と第2主成分からわかります。
例えば、下記は20列使用してK-meansクラスタリングを実行したものとなりますが、第1主成分で43.4%、第2主成分で17.9%と2つ合わせて全ての変数のばらつきの61.3% を表現できていると捉えることができます。
残りの38.7%のデータのばらつきについては、第3主成分以降で説明がつくばらつきになっています。
ちなみに、K-Meansクラスタリングの中で主成分分析を行っているのは、あくまで「バイプロット」タブで表示するためだけに行っているものであり、クラスタリングする際のアルゴリズムとは別の処理となります。
バイプロットの詳細については、こちらの「主成分分析(PCA)の紹介」のセミナーにて紹介していますので、そちらをご覧ください。
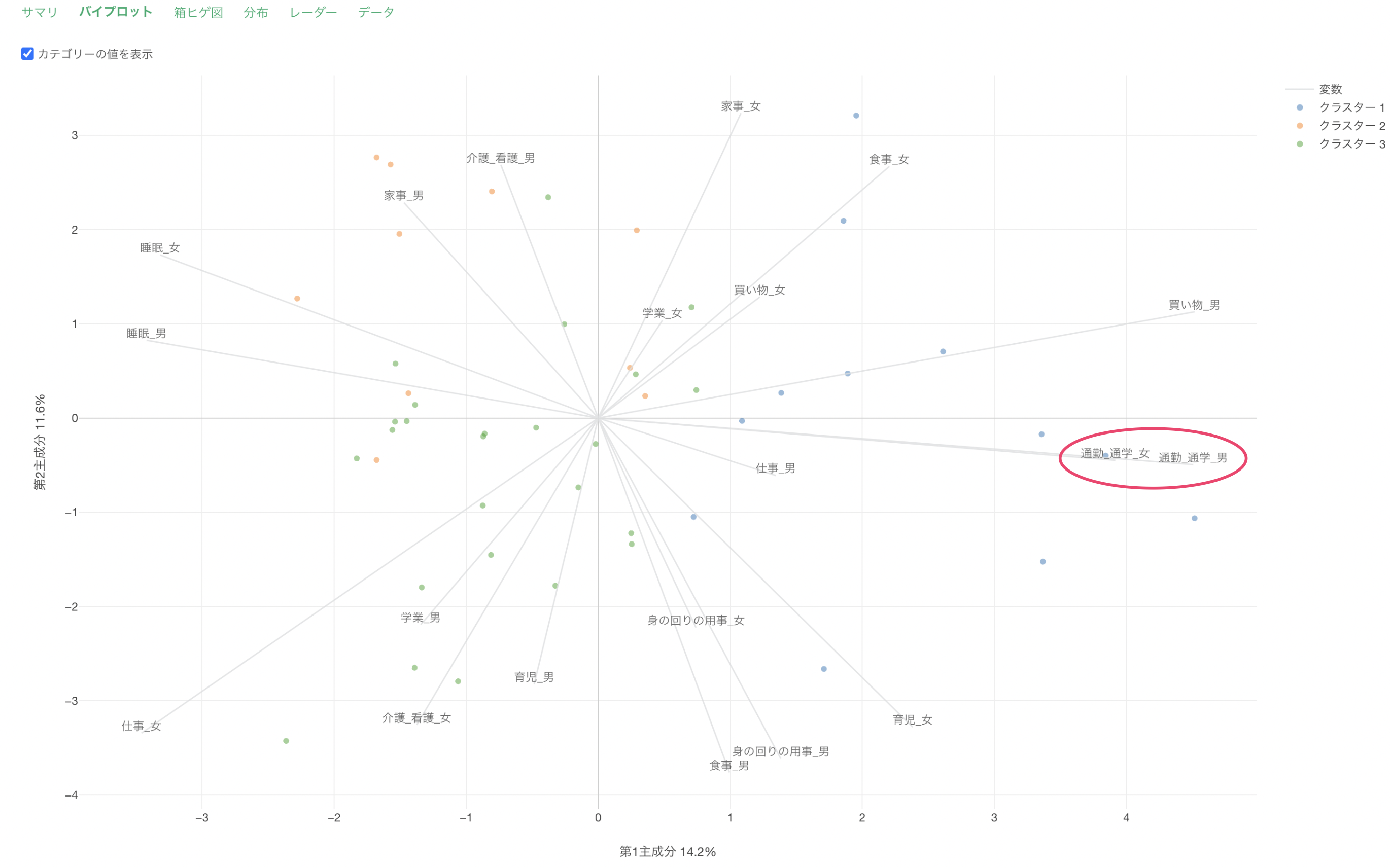
Q: バイプロットタブに表示される変数の軸線はどのように決まっていますか?
上述した「バイプロットタブに表示されている第1主成分、第2主成分は何を表しているのでしょうか?」と関連していますが、それぞれの変数の軸線は主成分分析を実行した際の第1主成分、第2主成分のスコアをもとに位置が決まっています。
Q: バイプロットタブのデータをエクスポートしたときの、それぞれのデータは何を表すのでしょうか?
PC1(第一主成分)はそのままの列名となっていますが、ObservationはPC2(第二主成分)の値となっています。
また、measure_nameはクラスタリングに使用した変数(数値列)を表しており、variablesはバイプロットでそれぞれの変数の軸を表現する時に使用されている値となっています。
下記は、左側がK-meansのバイプロットで、右側がエクスポートしたデータをもとにチャートで可視化をしています。
X軸にPC1, Y軸にVariablesを割り当てていますが、元のバイプロットと同じく、それぞれの変数の軸がある位置が表現されています。