幾何平均の計算方法

このノートでは幾何平均の計算方法を紹介します。

幾何平均とは

幾何平均は、n個の正の数値の積のn乗根として定義される平均です。これは、比率やパーセンテージの平均を求める際に特に有効で、各数値が同じ比率で増減する場合の平均的な増減率を求めることに適しています。

たとえば、ある投資の年間リターンが1年目に10%、2年目に50%、3年目に30%だったとします。

これらのリターンの幾何平均を求めるには、各リターンを1に足した数（1.10、1.50、1.30）をすべて掛け合わせ、それを年数の逆数（この場合は1/3）で累乗根を取ります。

また計算式は以下のようになります。

\[ \text{幾何平均} = \left( \prod_{i=1}^{n} x_i \right)^\frac{1}{n} = \sqrt[n]{x_1 \cdot x_2 \cdot \ldots \cdot x_n} \]

このとき、xiは各数値を指し、 nは数値の総数を表します。先程の例で幾何平均を計算したい場合、以下の計算式にて求めることができます。

\[ \text{幾何平均} = \sqrt[3]{1.10 \times 1.50 \times 1.30} \]

上記を計算すると、 3年間の投資の平均成長率が得られます。この平均値は、各年に同じ成長率が適用された場合の平均的な成長率と解釈できます。

以下にExploratoryの中で幾何平均の計算をする2つの方法を紹介します。

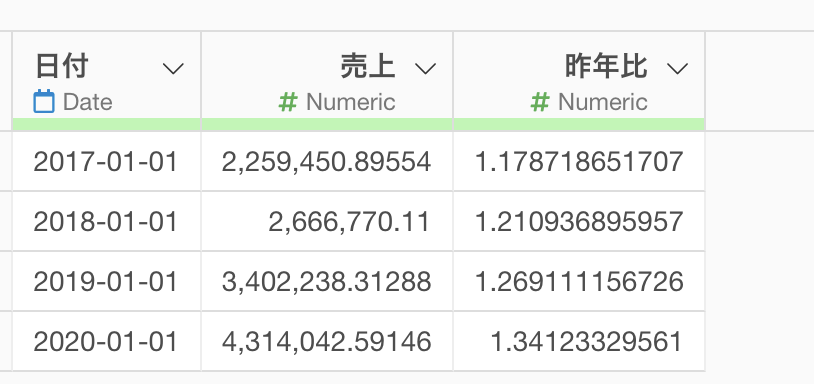
例えば以下のような売上と昨年比のデータがあったとします。

昨年比の列ヘッダーメニューから「集計」を選択します。

集計のダイアログが開いたら、値に「カスタム」を選択します。

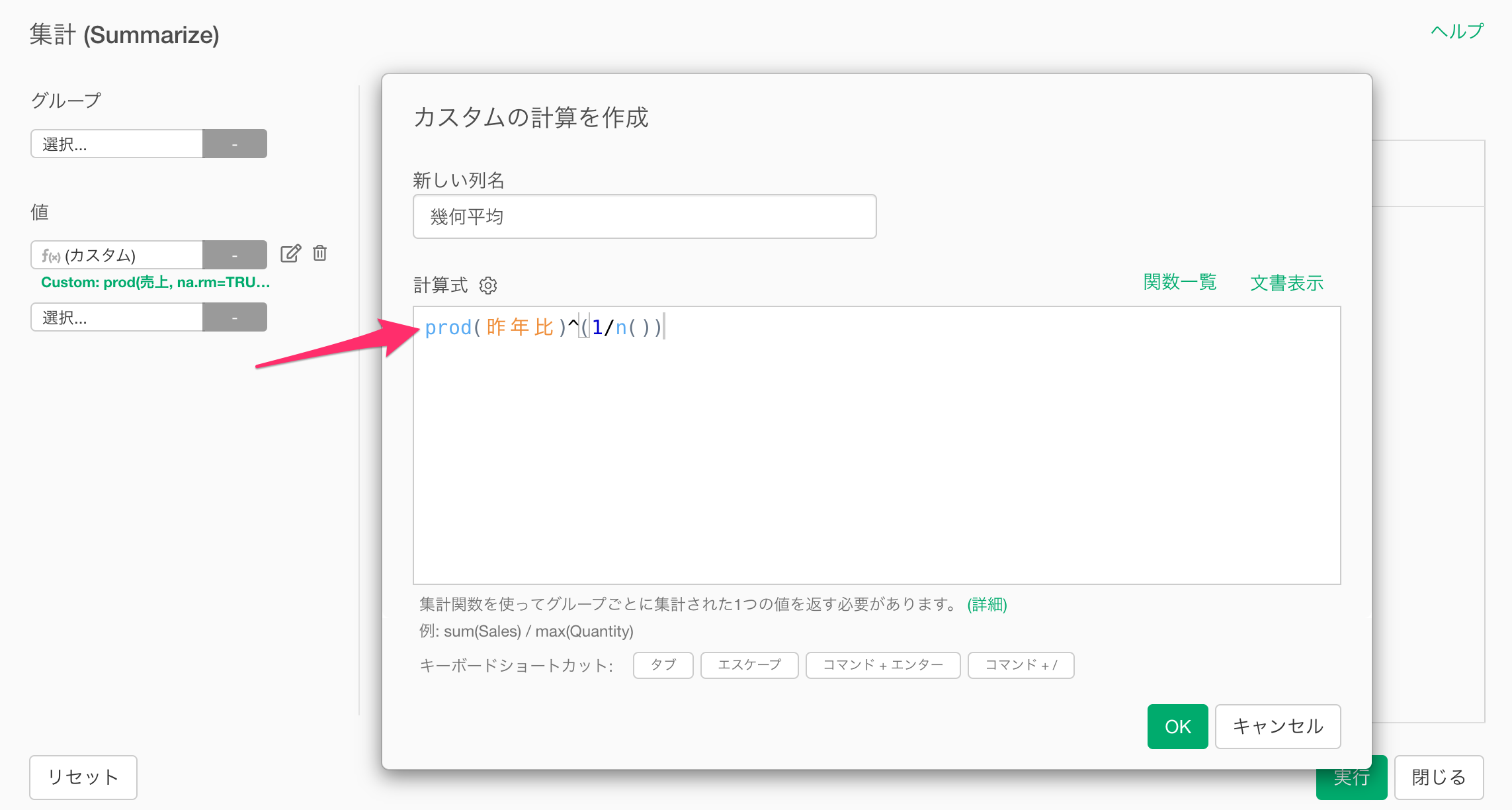
計算式に以下の内容を入力し、「OK」ボタンをクリックします。

prod(昨年比)^(1/n())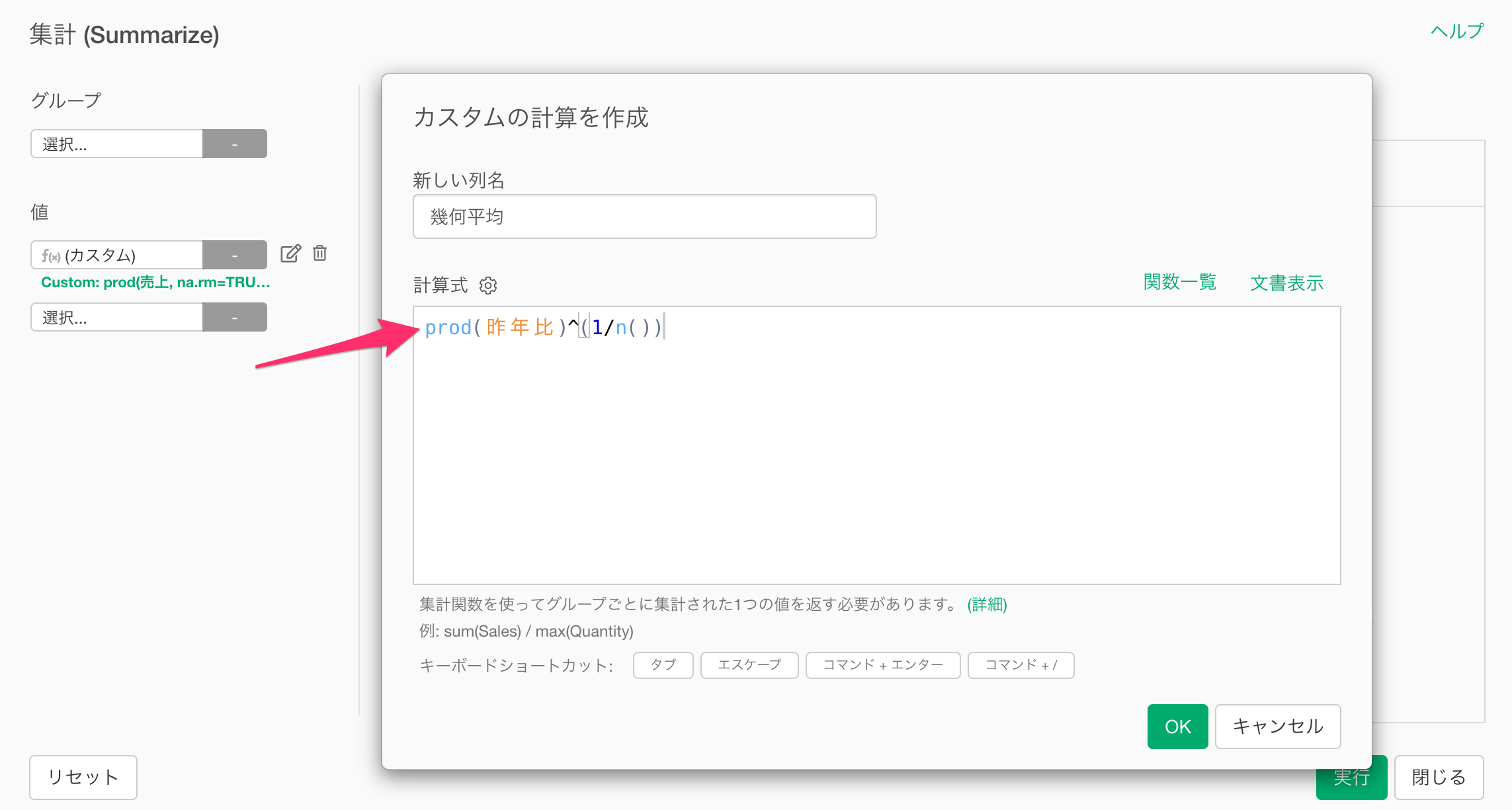

なおprod関数は指定した一連のデータの数値（今回の例で言うと毎年の昨年比の値）を全て乗算した値を返す関数で、n関数は行数を返す、言い換えれば、データの個数を返す関数です。

上記の計算式により、昨年比の各数値を掛け合わせた積の値をn乗根することができ、幾何平均を計算できるわけです。

プレビューボタンをクリックすると幾何平均を計算できていることが確認できるので、実行ボタンをクリックします。

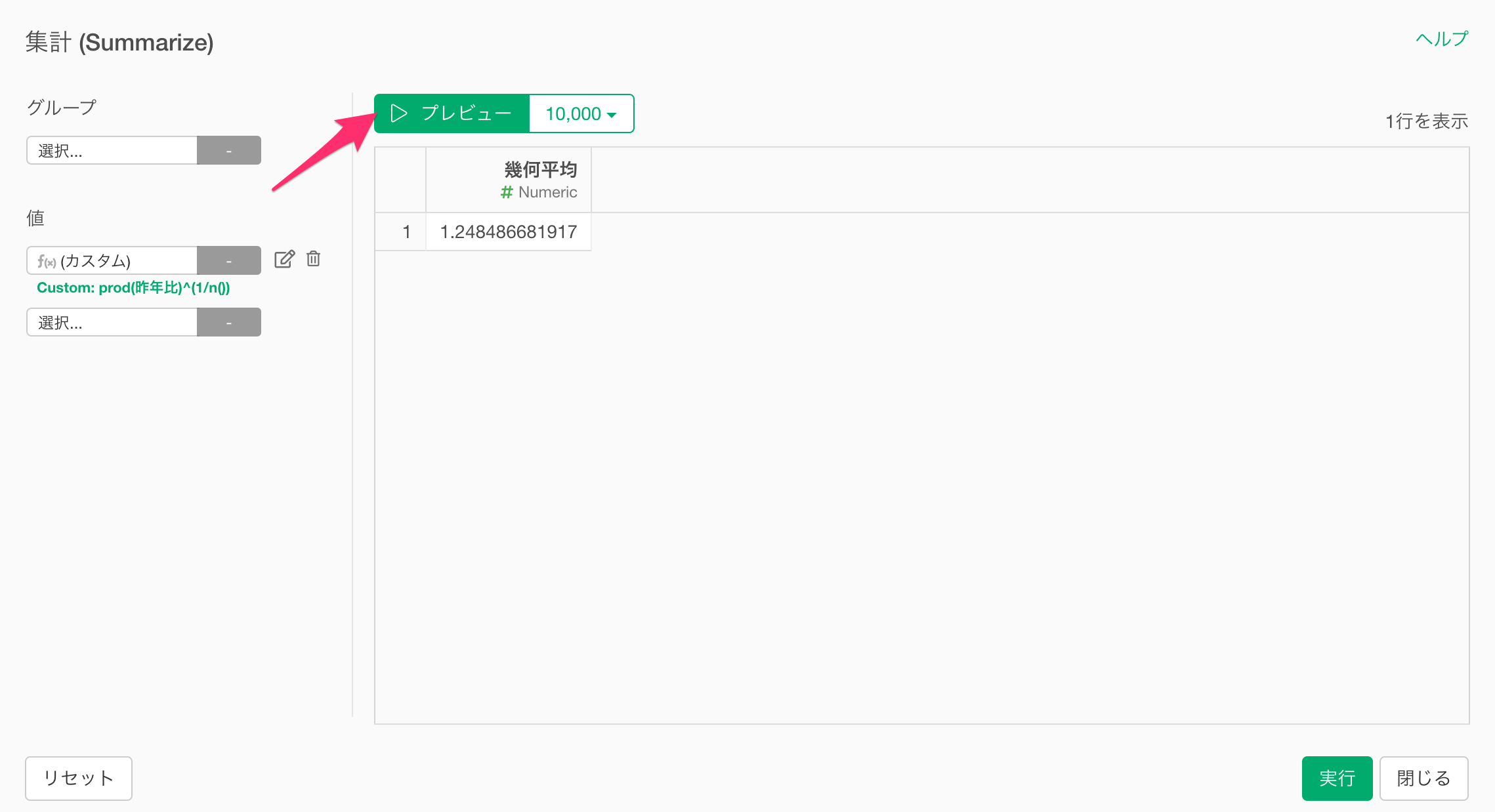
幾何平均を集計できました。

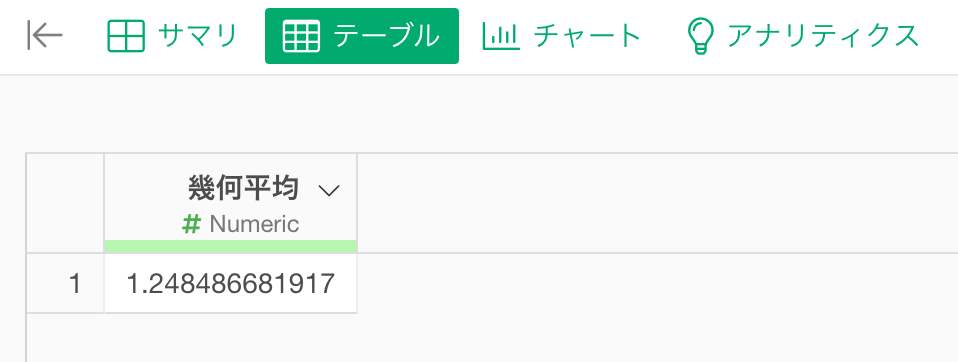
なお、このとき、幾何平均を求めたい列に欠損値があると、正しく値が計算できないため、フィルタで欠損値を除外しておいてください。

前述した数式を使って幾何平均を集計する方法もありますが、EnvStatsパッケージのgeoMean関数を利用して、幾何平均をより簡単に集計する方法もあります。

geoMean関数を使う時にはEnvStatsのパッケージをインストールします。

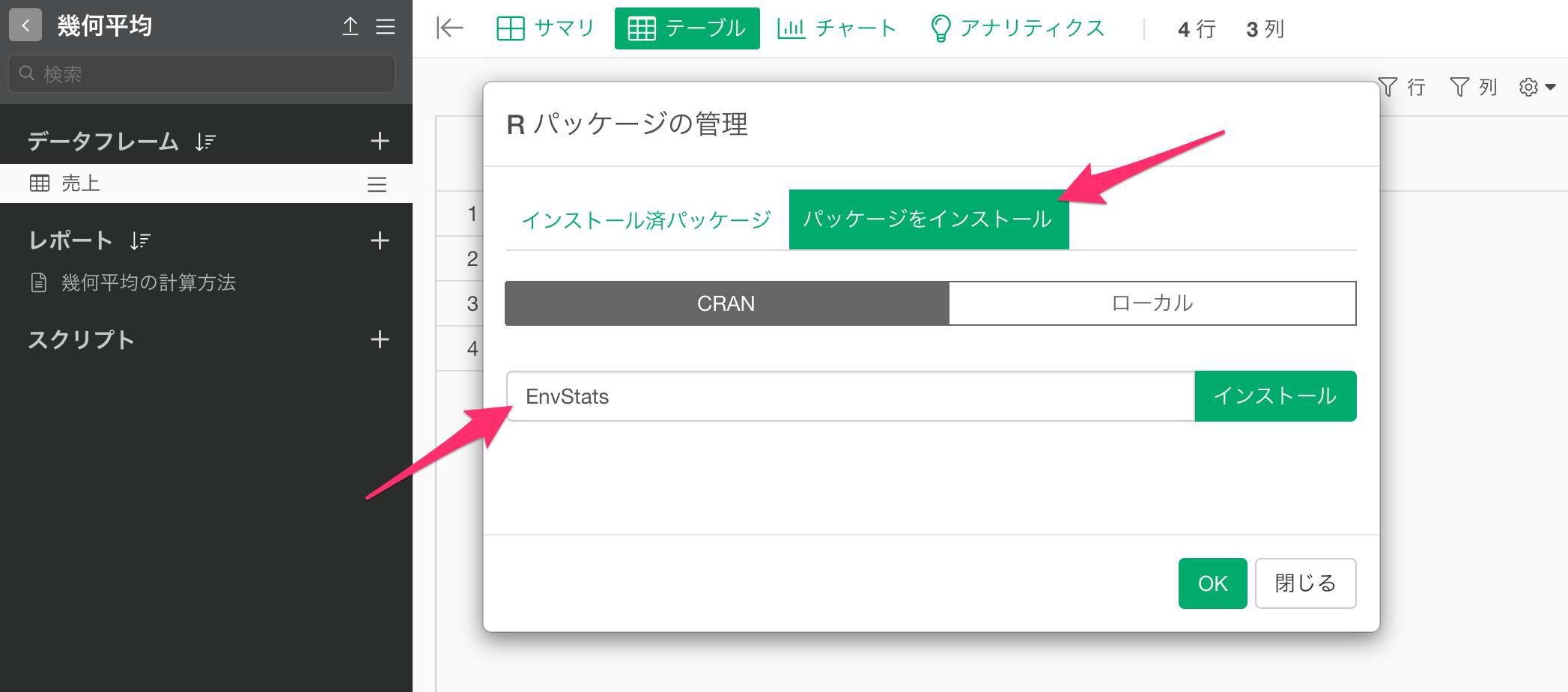
プロジェクトメニューから「Rパッケージの管理」を選択します。

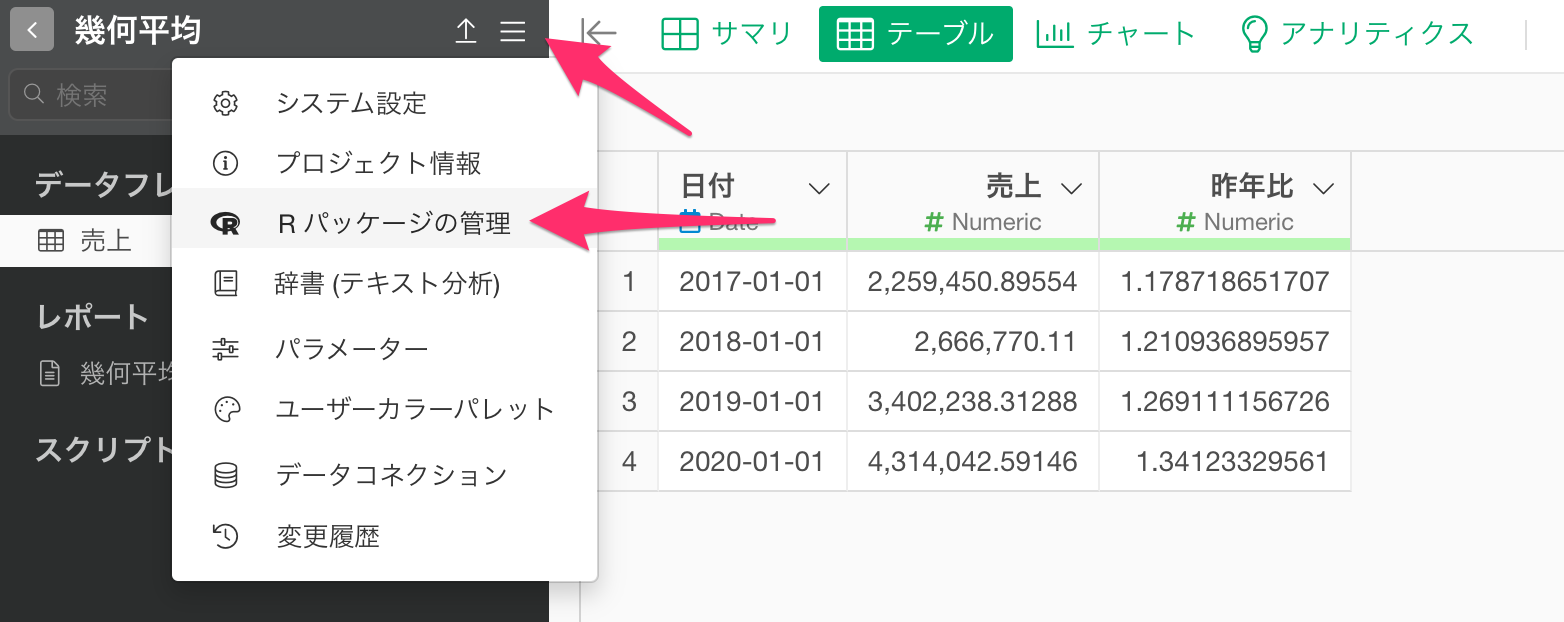
パッケージインストールのタブに移動し、「EnvStats」とタイプし、インストールボタンをクリックします。

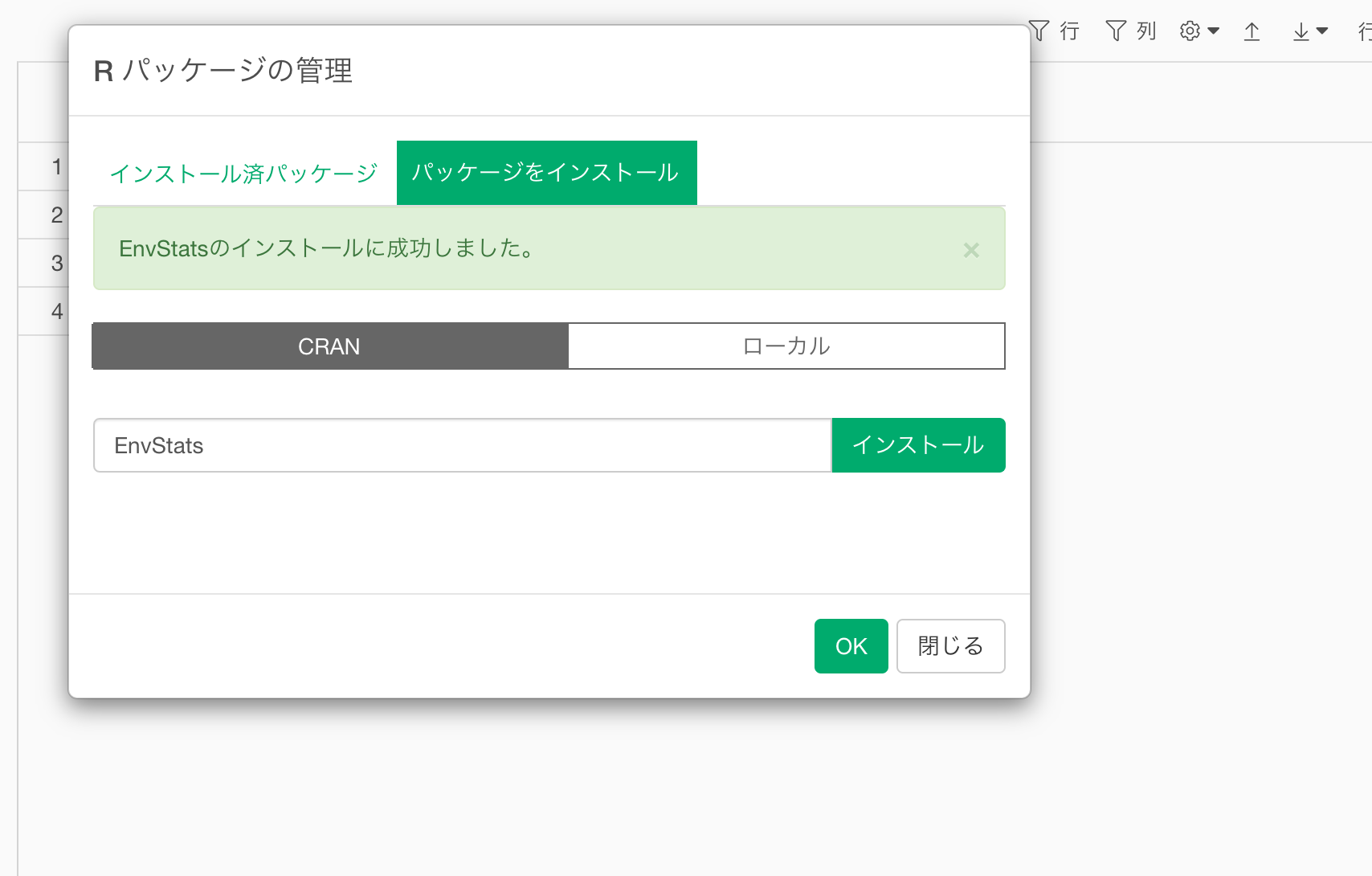
パッケージのインストールに成功したらOKボタンをクリックします。

続いて、「昨対比」の列ヘッダーメニューから「集計」を選択します。

集計のダイアログが開いたら、値に「カスタム」を選択します。

計算式に、幾何平均を計算するgeoMean関数を使って、以下の内容を入力し、「OK」ボタンをクリックします。

geoMean(昨年比, na.rm = TRUE)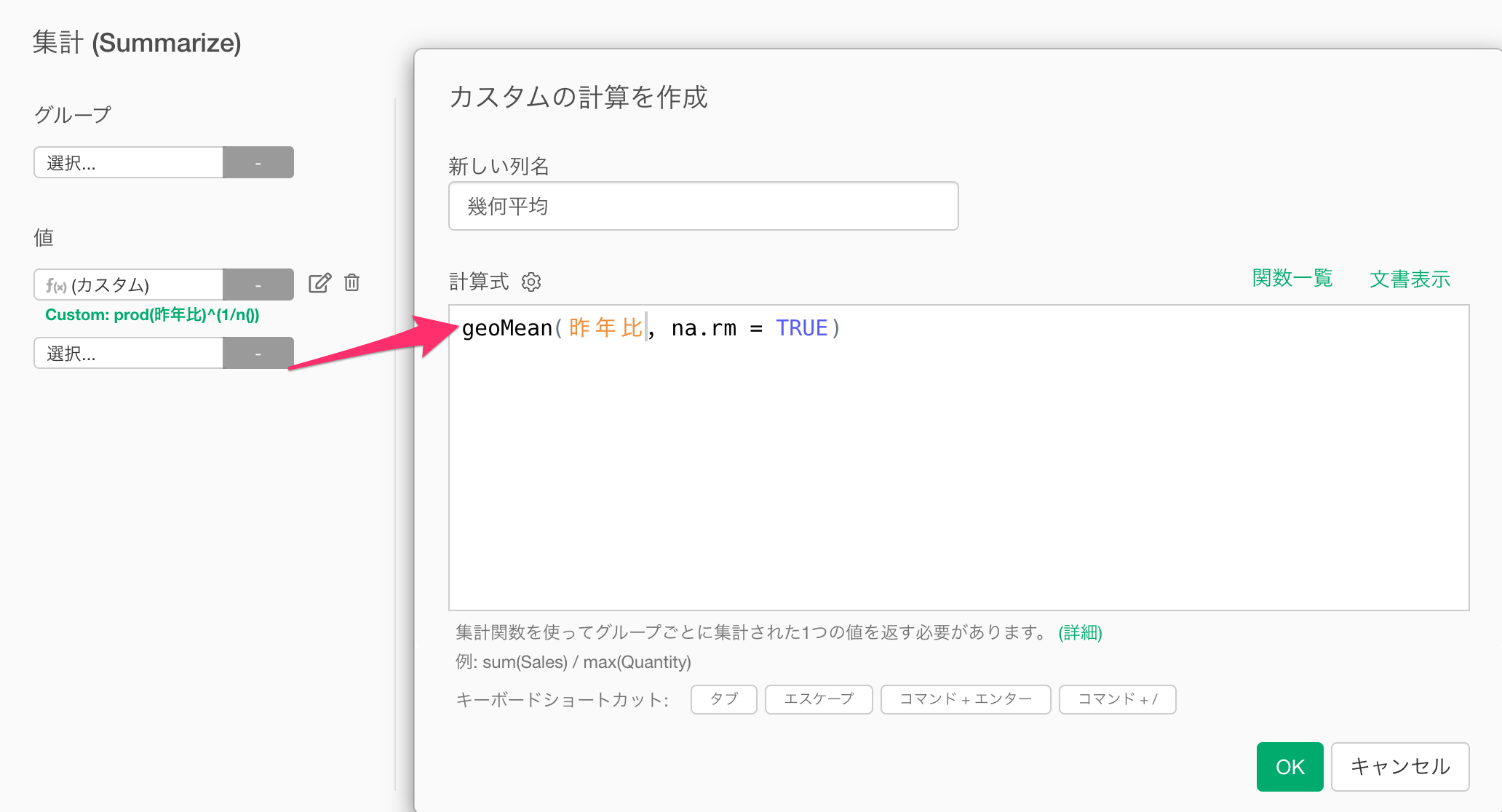

なお、na.rmは欠損値の処理を指定する引数で、引数にTRUEを指定したときには欠損値を削除したうえで、幾何平均を計算するので、事前に欠損値を取り除いておく必要がありません。

プレビューボタンをクリックすると幾何平均を計算できていることが確認できるので、実行ボタンをクリックします。

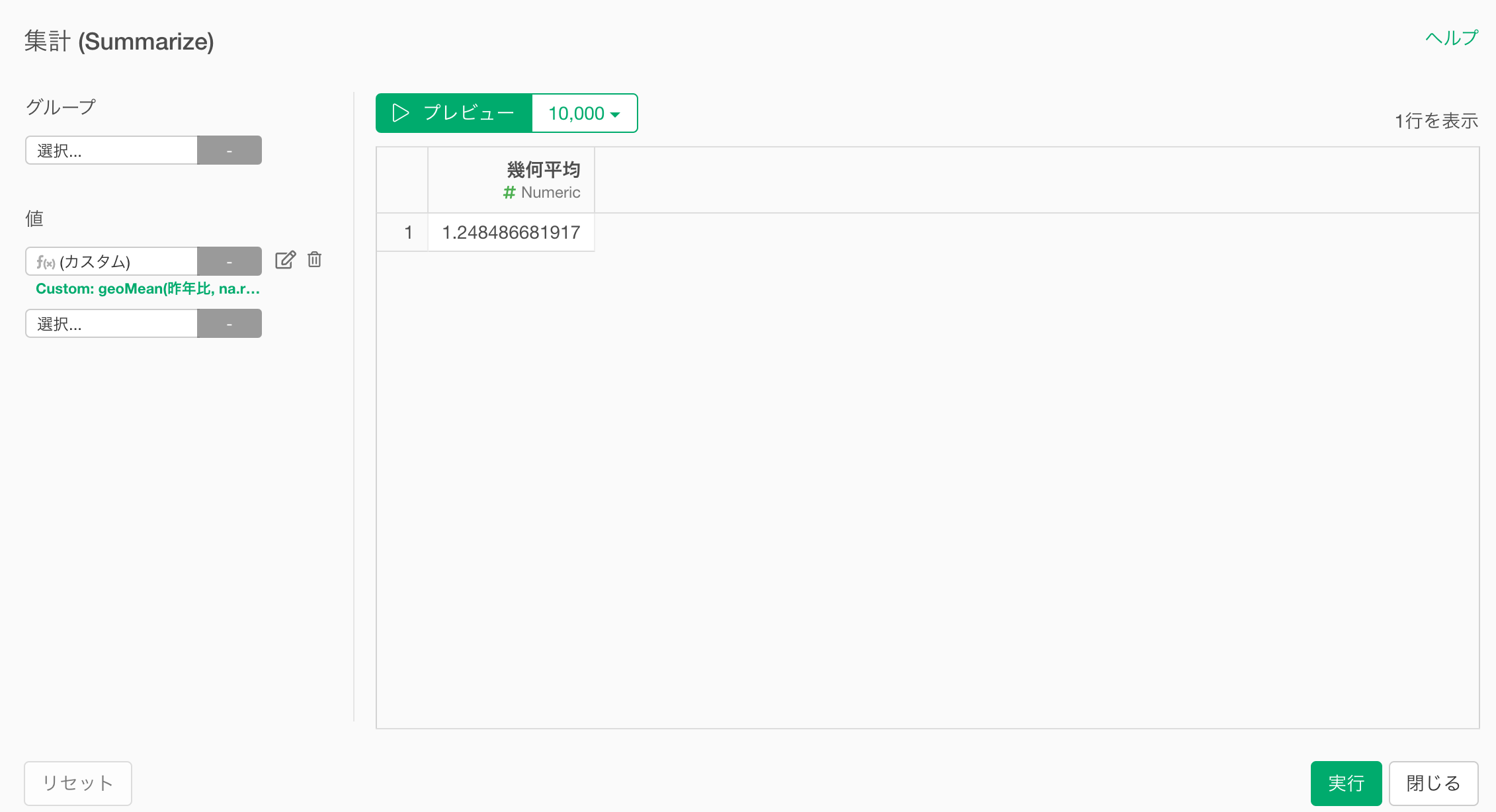
幾何平均を集計できました。