コックス回帰の使い方
コックス回帰の使い方や結果の解釈の仕方、よくある質問を紹介します。
ロジスティック回帰は、顧客がサービスの利用を開始するかどうかといった、「はい」か「いいえ」で決まるようなデータを目的変数に取るようなアルゴリズムでした。
しかし、例えばサブクリプション型のビジネスにおける顧客のキャンセルについて考えるときは、「サービスをキャンセルするかどうか」ではなく、「どれくらいの期間でキャンセルが発生したのか」が重要です。
そこで、生存曲線を使った「生存分析」を実施することで、観察対象の生存時間とイベント(例: サービスのキャンセル)の発生の関係を可視化できますが、生存分析のアルゴリズムのコックス回帰を使うことで、下記の質問にも答えられます。
- このデータ(予測変数)を使うことで、あるタイミング(例:サービスの利用開始から1年後)における生存状態(例:サービスのキャンセル)のTRUE/FALSEをどれだけ上手く分けられているのか。
- どの変数が、あるタイミングにおける生存状態を予測するうえで重要なのか。
- 予測変数の値が変わると、生存曲線はどのように変わるのか。
- とある観察対象(例: 顧客、従業員)の生存確率が50%を下回るのはいつか。
- とある観察対象に注目したときに、1ヶ月後の生存確率はどの程度か。
必要なデータ
コックス回帰のモデルを作成するためには、**1行が1観察対象(例:1行が1顧客)**のデータが必要です。
また、以下の情報も列に必要です。
- 開始時期:観察対象の観察の開始時期を表す、Data(日付)型、またはPOSIXct(日付時間)型の列
- 終了時期:観察対象の観察の終了時期を表す、Data(日付)型、またはPOSIXct(日付時間)型の列
- 生存状態:観察対象のイベントのステータスを表す、ロジカル型の列(例:キャンセル、解約、離職、死亡など)
- 予測変数:生存状態を予測するための列(データタイプに制限はありません)
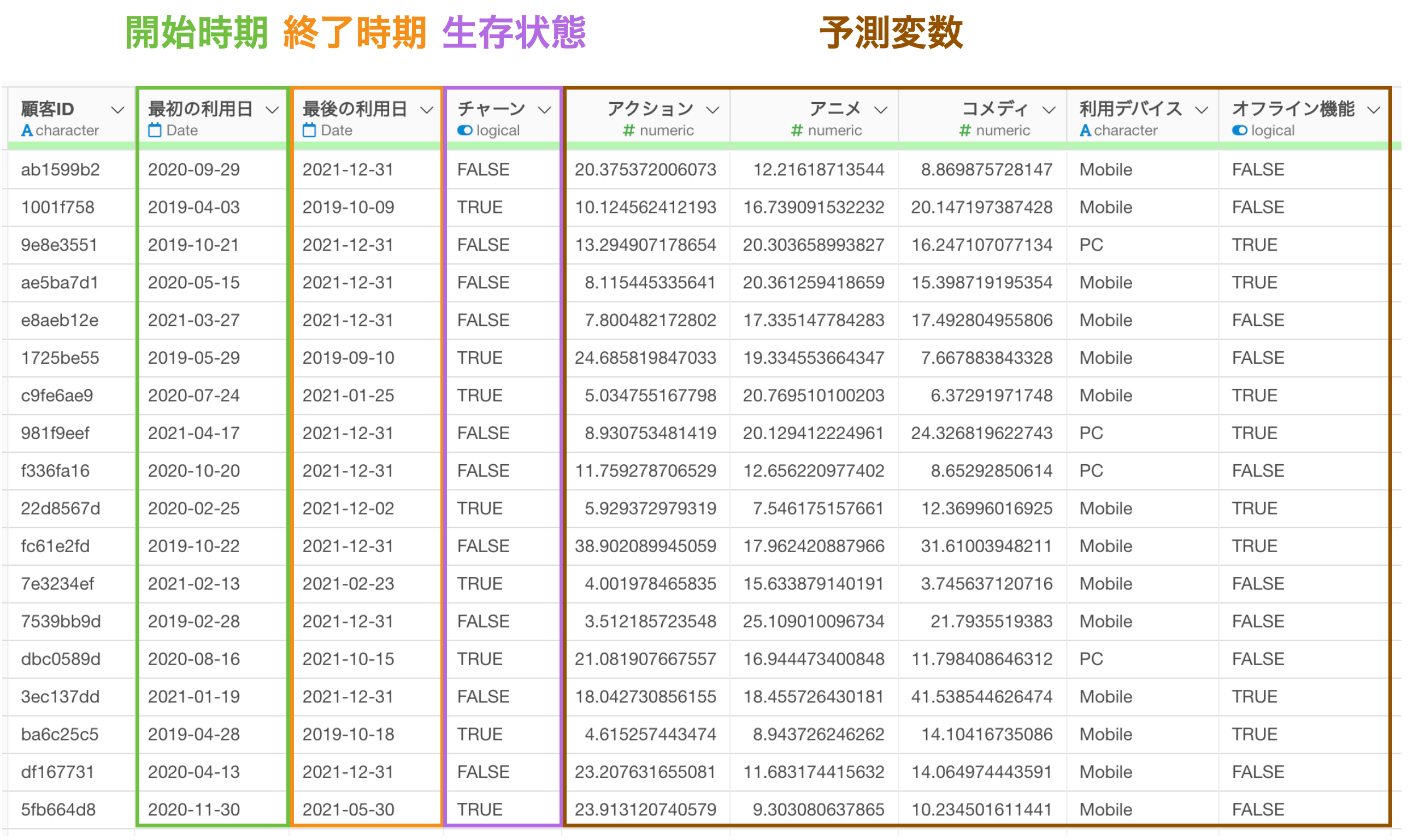
サンプルデータ
今回はサンプルデータとして、Netflixのような動画視聴のサブスクリプション・サービスのデータを使用していきます。
このデータは1行が1顧客のデータで、列にはコンテンツの視聴時間や、主な利用デバイス、サービスが提供する機能の利用状況、年齢や性別などの属性の情報があります。
コックス回帰のモデルを作成する
今回は顧客のある時点での生存確率を予測するコックス回帰のモデルを作成します。
アナリティクス・ビューに移動して、タイプに「コックス回帰」を選択します。
「開始時期」に「最初の利用日」を選択します。
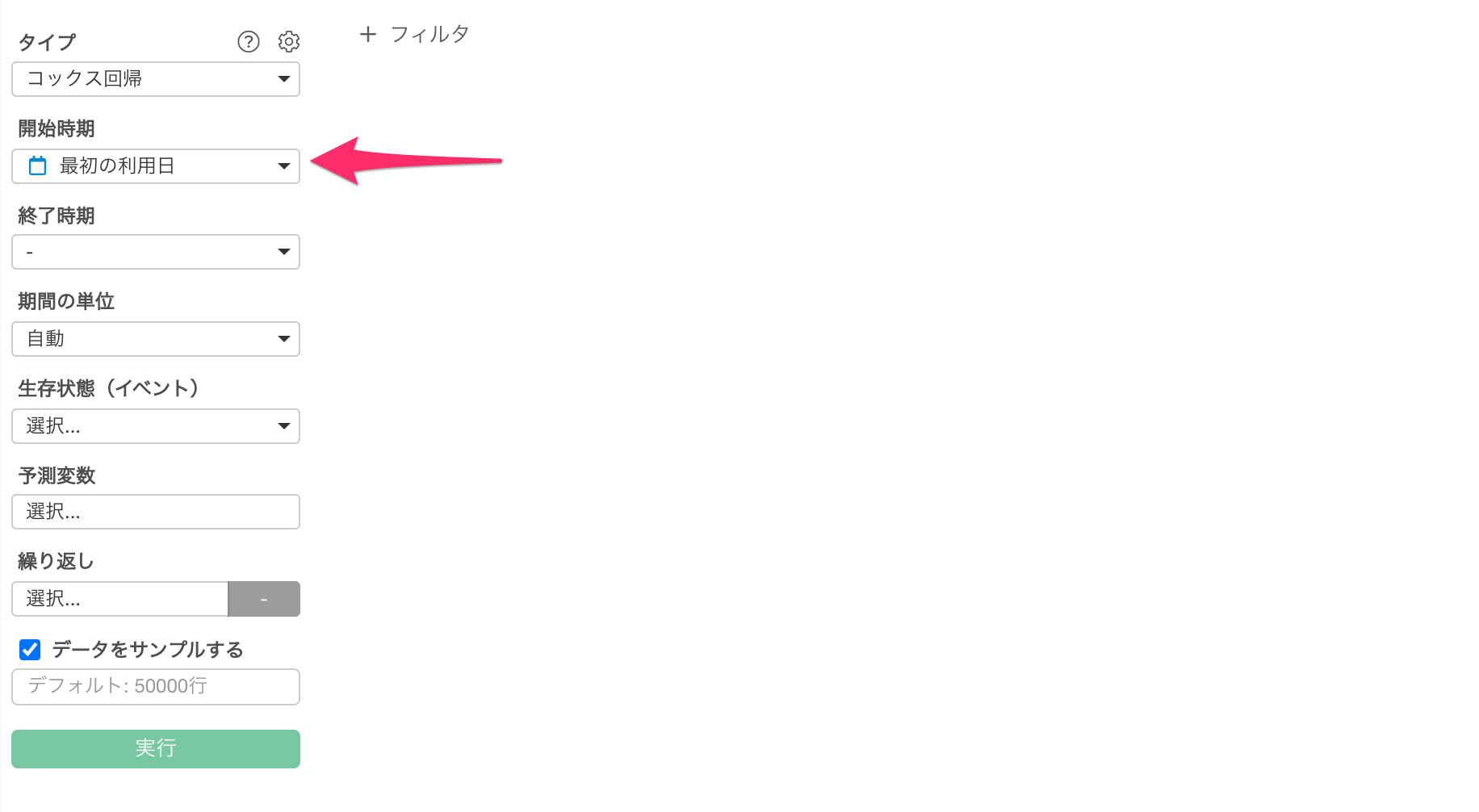
「終了時期」に「最後の利用日」を選択します。

「期間の単位」からは生存期間の単位を設定できます。なお、デフォルトは「自動」になっており、自動で最適な「期間の単位」が設定されます。

生存状態に「キャンセル」を選択します。

続いて、予測変数を選択します。

予測変数を選択します。Shiftキーを押しながら列を選ぶことで、一気に列を選択できます。
「実行」ボタンをクリックします。
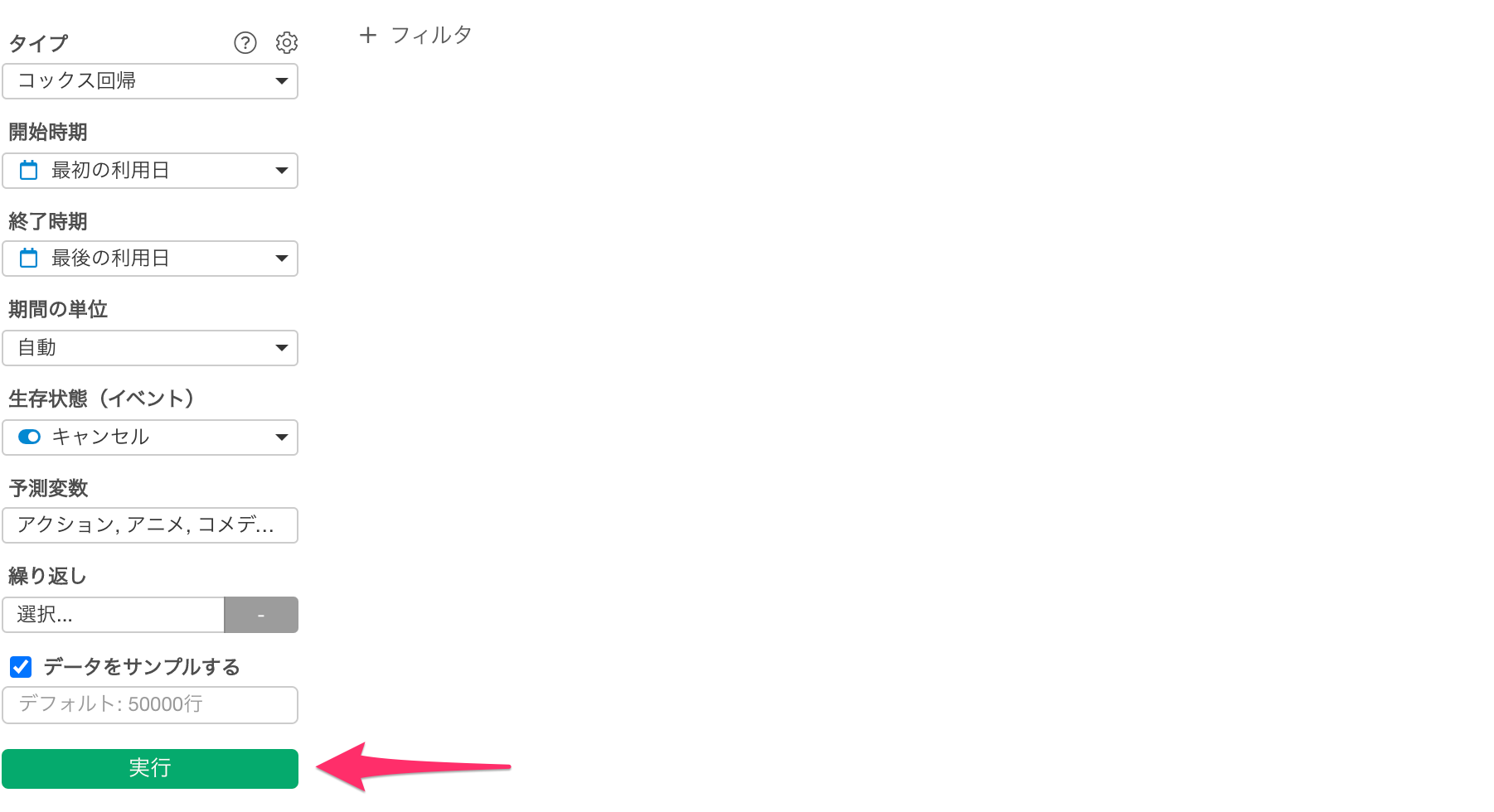
コックス回帰のモデルが作成されました。
結果の解釈
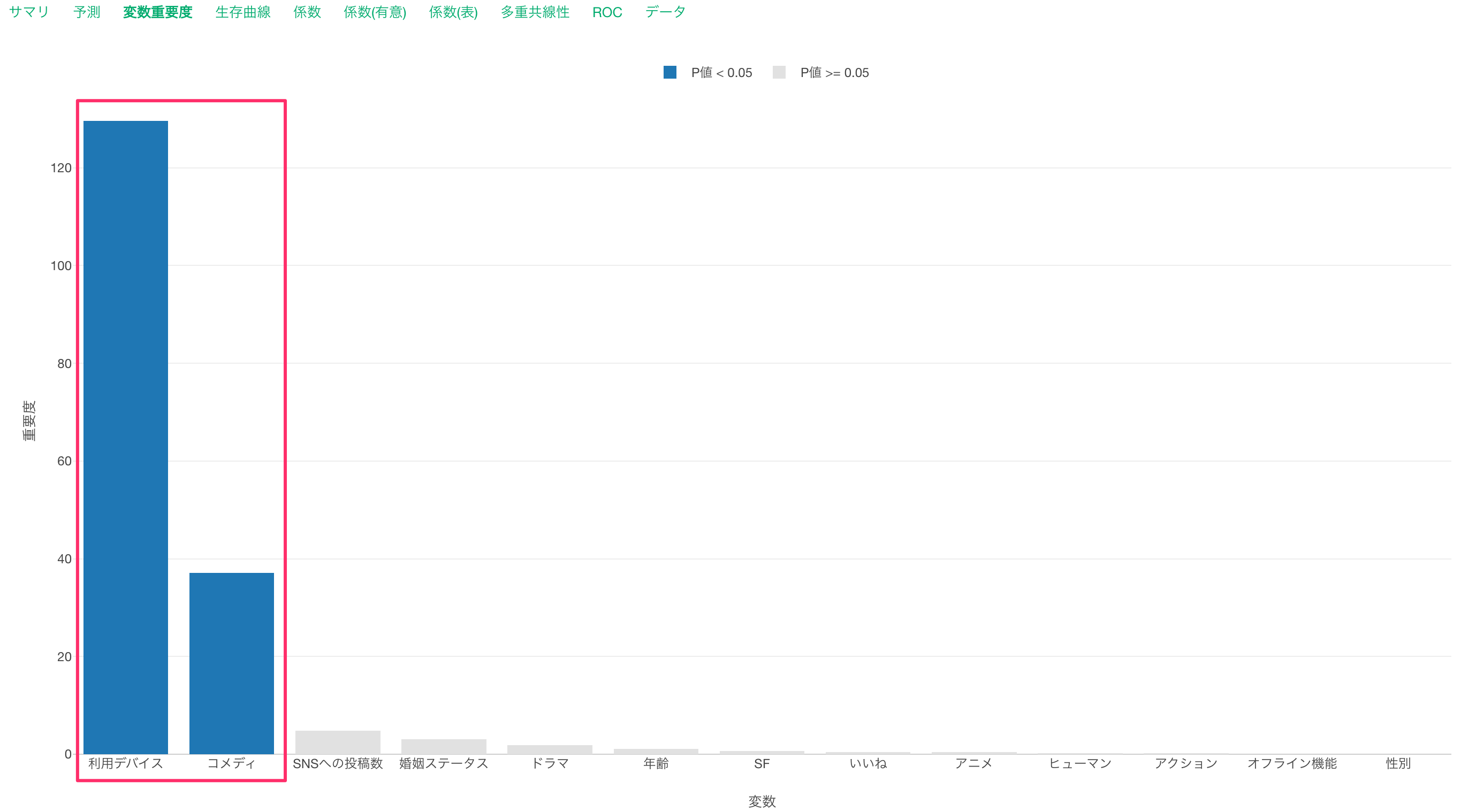
変数重要度
変数重要度タブでは、どの変数が生存曲線の傾きとより相関が強いのかや、予測する時により重要なのかを調べられます。
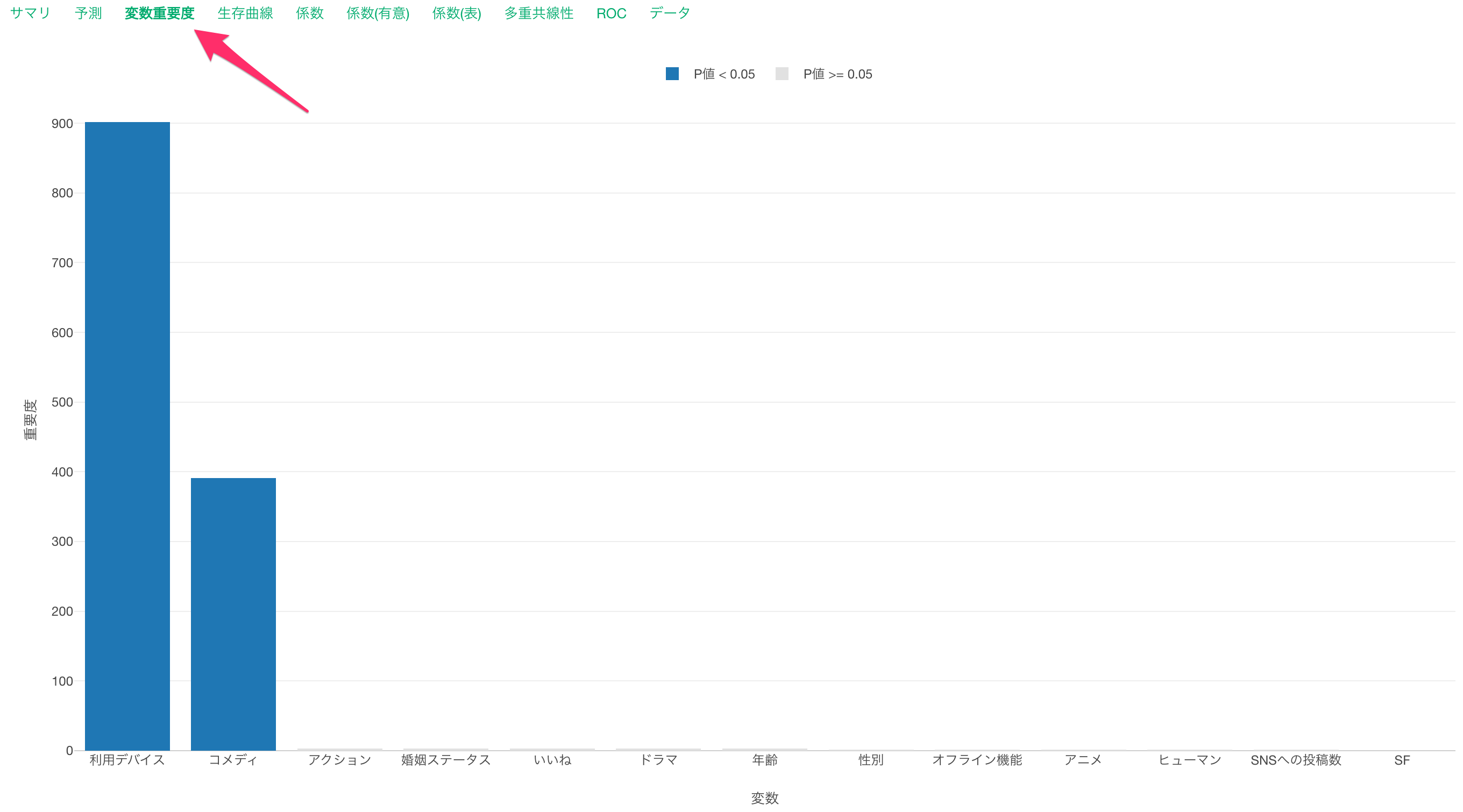
今回のデータでは「利用デバイス」がある時点のキャンセルを予測する上で最も重要な変数なようです。それ以外にも、コメディの視聴時間が、ある時点での顧客のキャンセルを予測する上で重要だとわかります。
変数重要度の詳しい説明については、こちらの「機械学習モデル - 変数重要度の仕組みと解釈」のセミナーをご覧下さい。
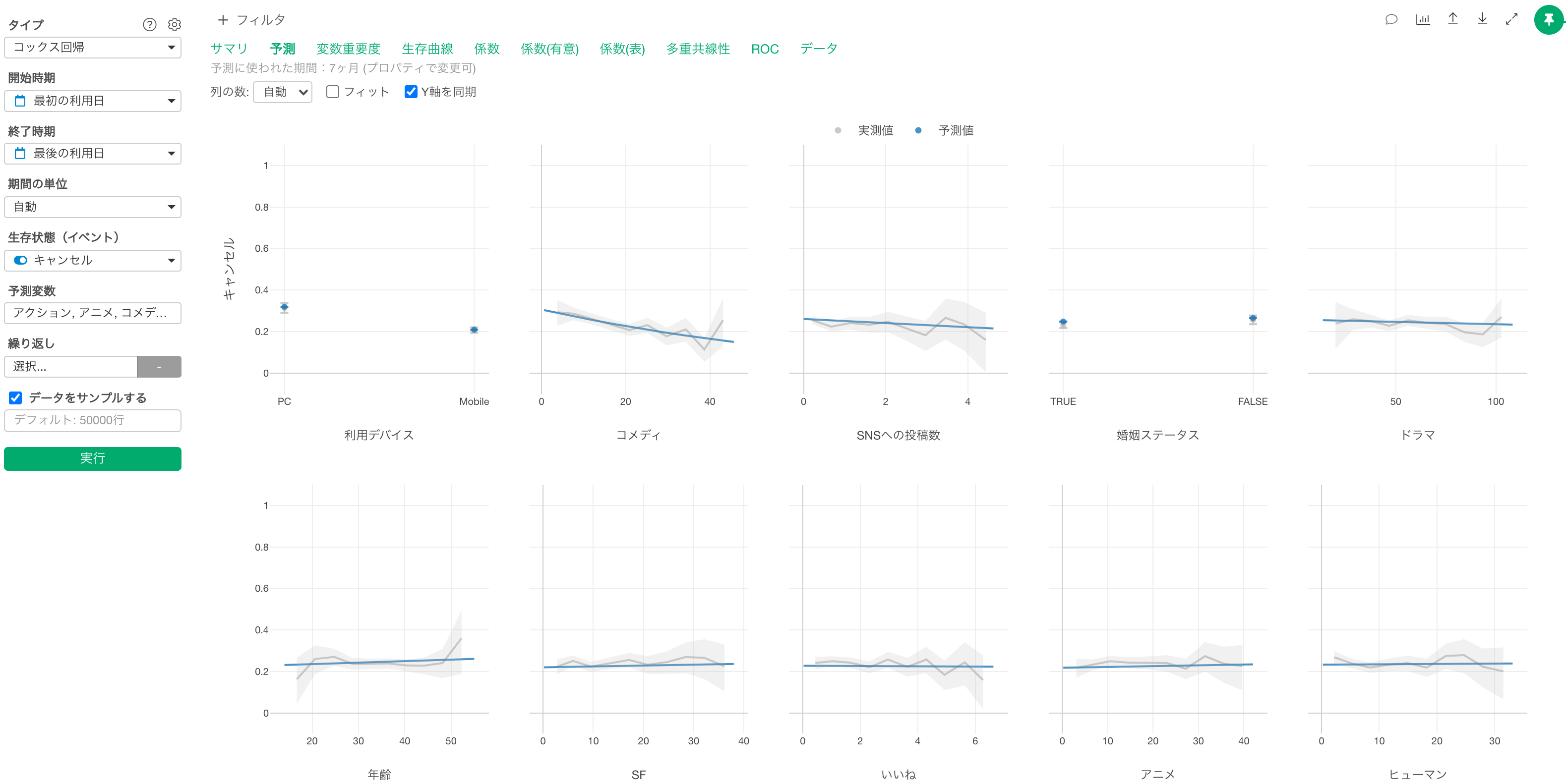
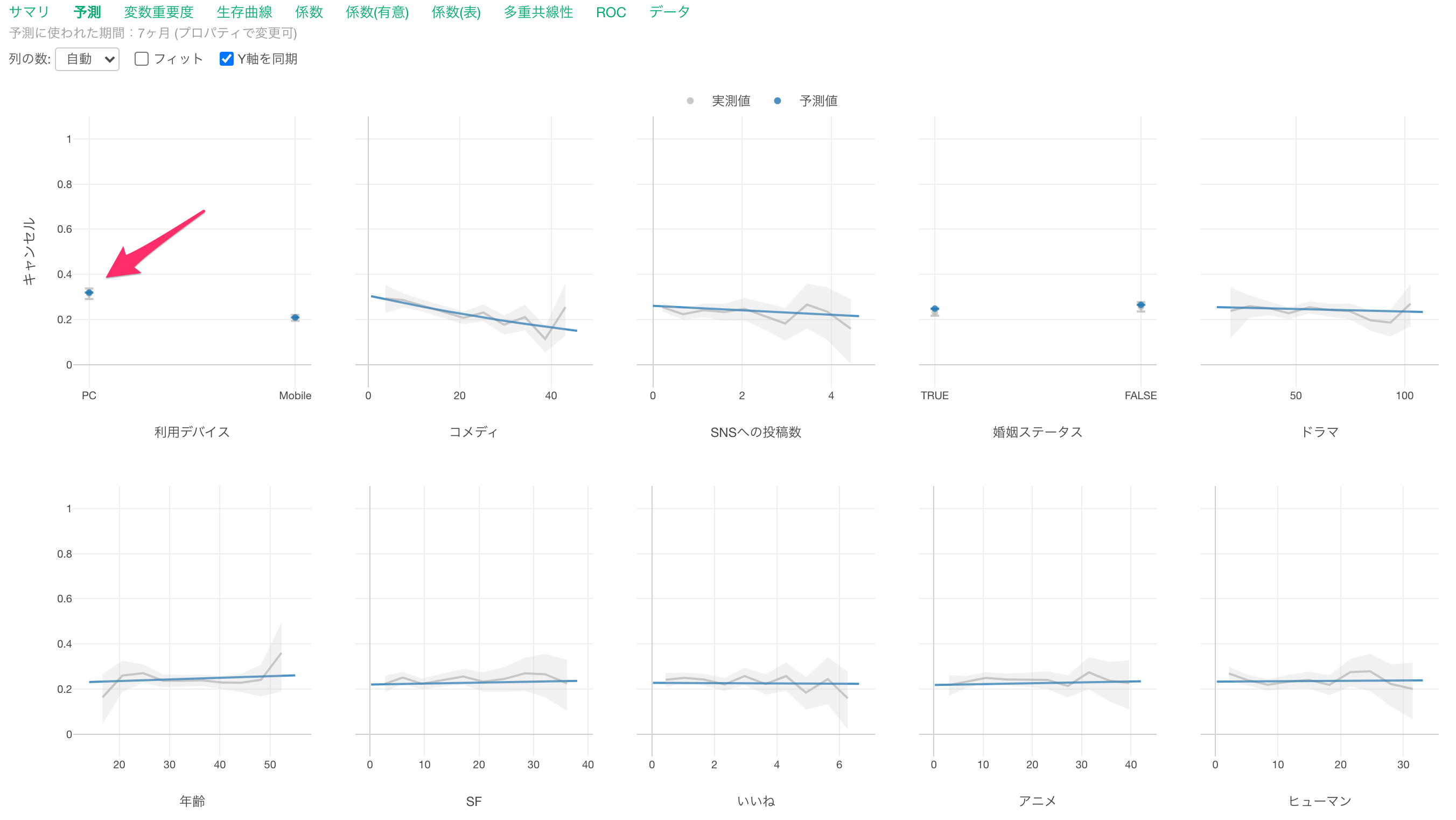
予測
予測タブでは、イベント(キャンセル)が発生した観察対象の平均生存期間において、それぞれの変数の値が変わると、生存状態がどのように変わるのかがわかります。
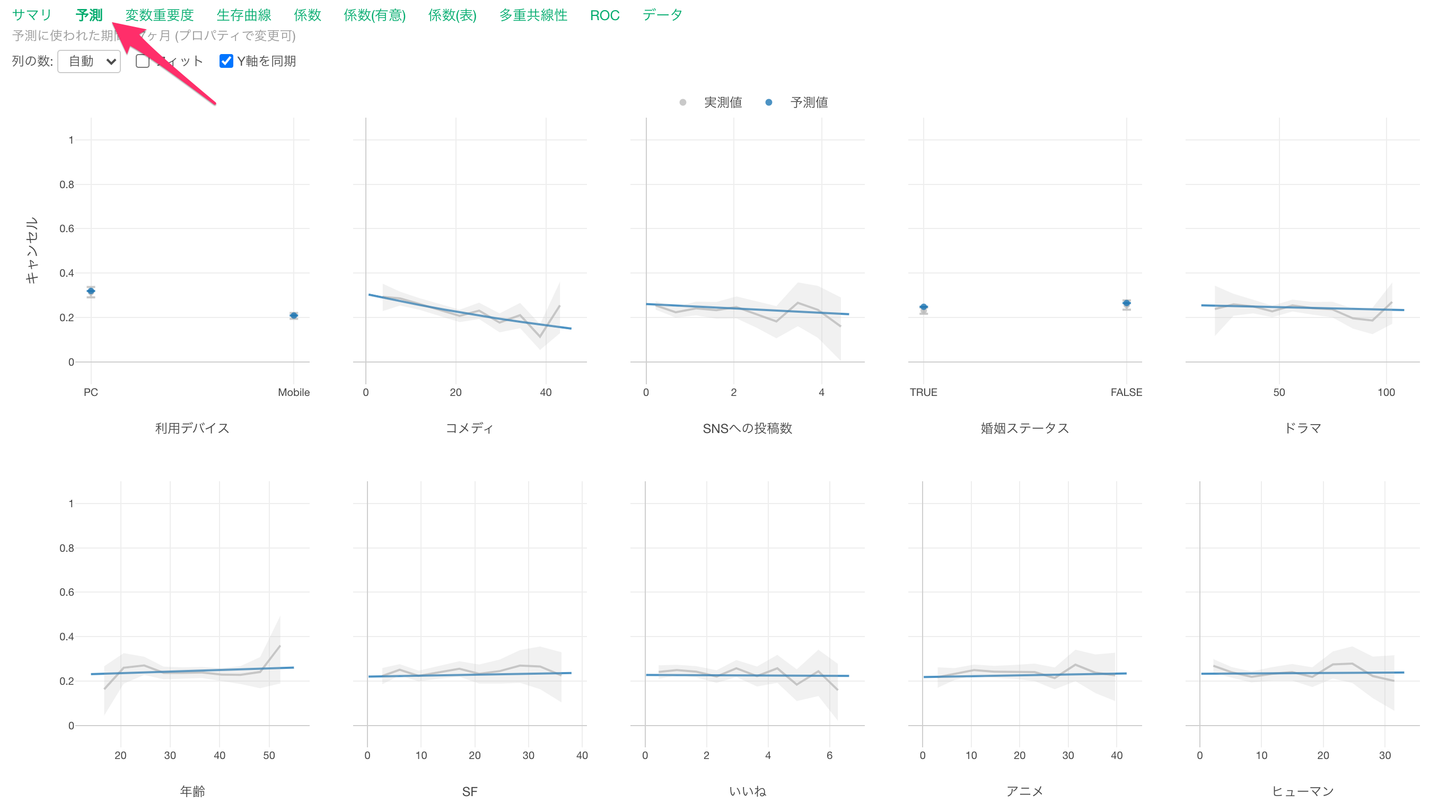
グレーの線は実測値を表しています。
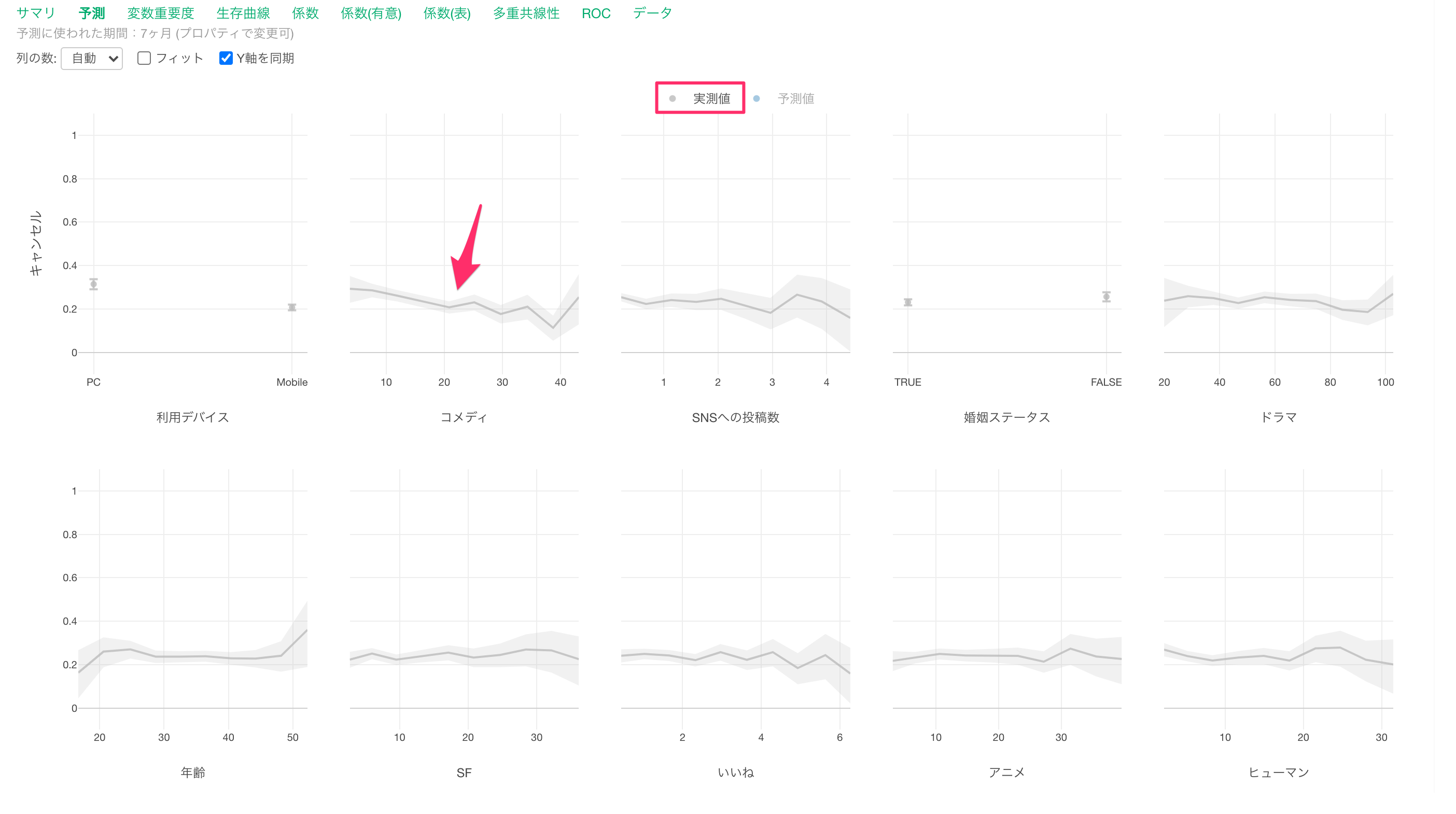
青い線は予測値を表します。
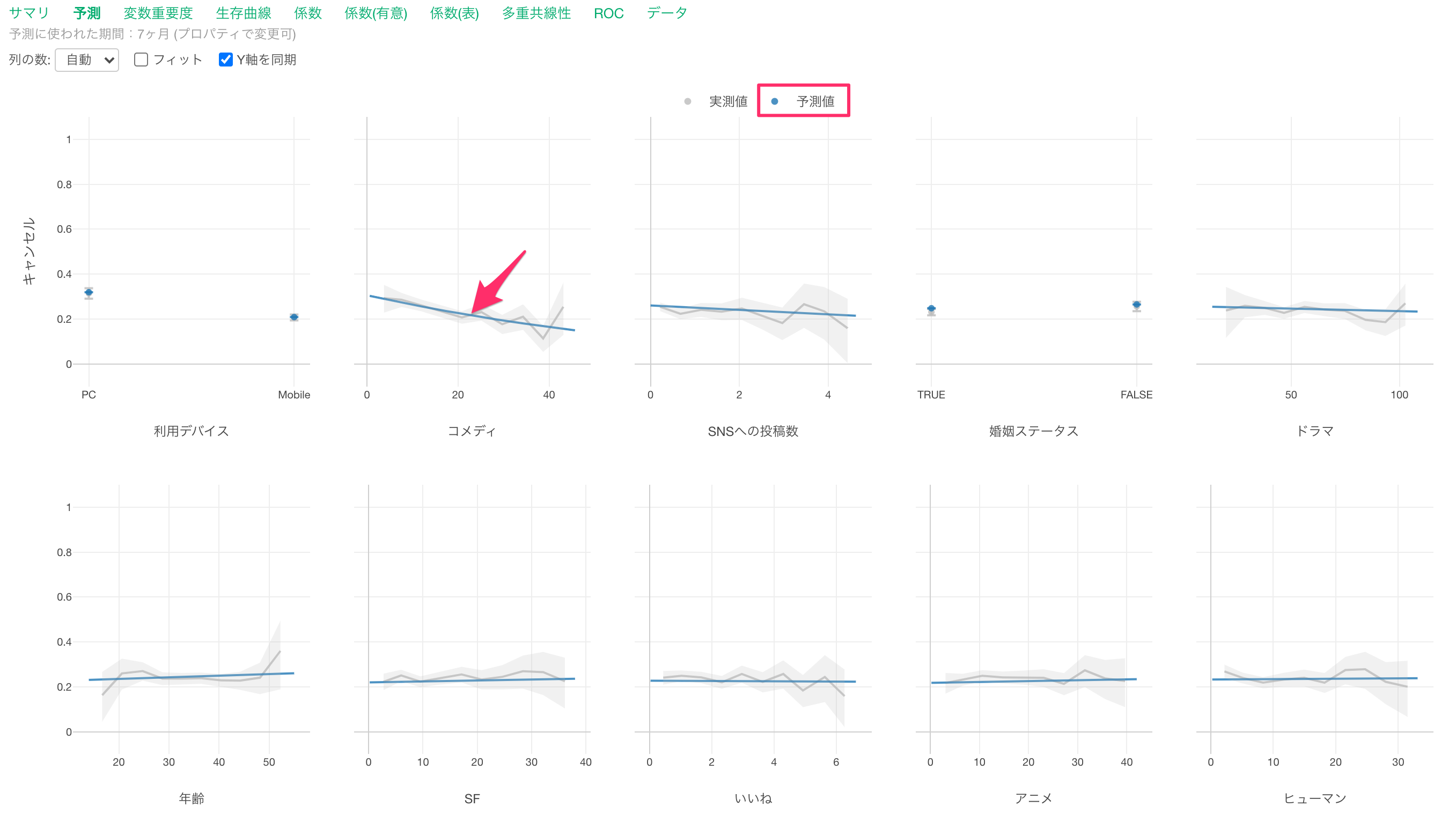
コメディの視聴時間が増えるとキャンセル率が高くなる関係があることがわかります。
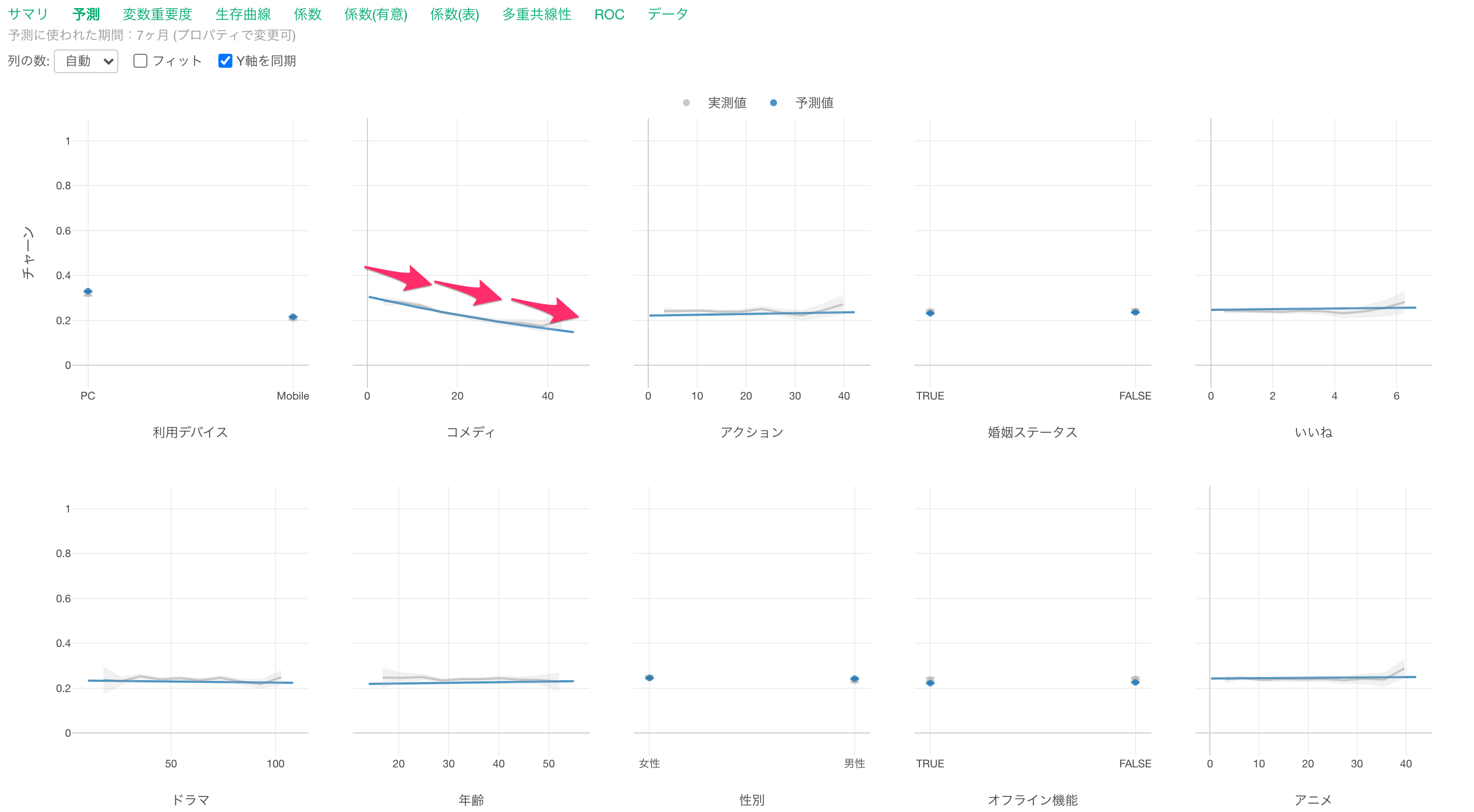
他の変数が一定だった時に、コメディの視聴時間の値が1上がるとキャンセルする可能性(ハザード比)が0.98倍になる関係があるようです。
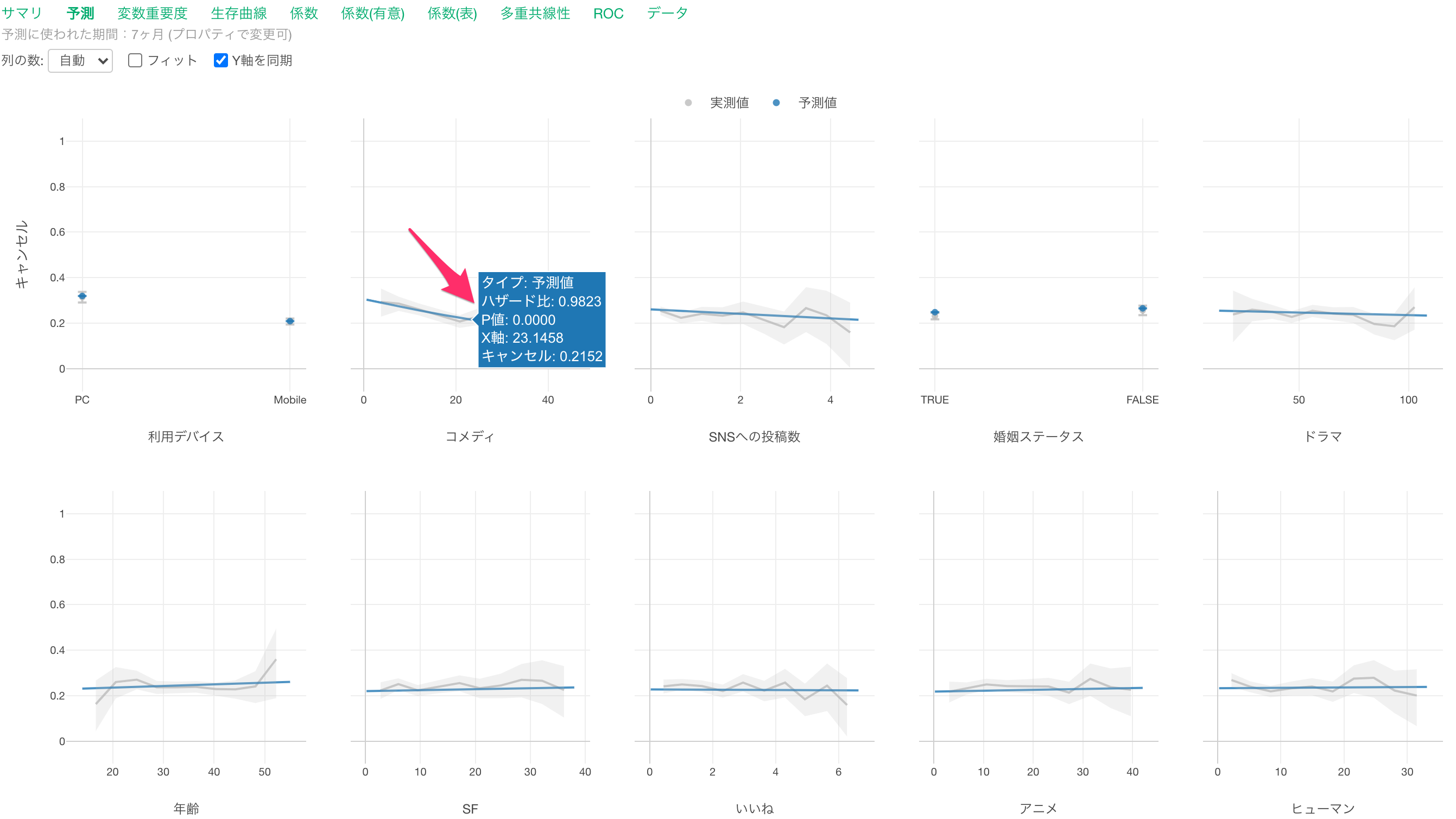
利用デバイスを見るとPC端末を主にしている場合は、モバイル端末を主に利用している場合に比べてキャンセル率が高いようです。
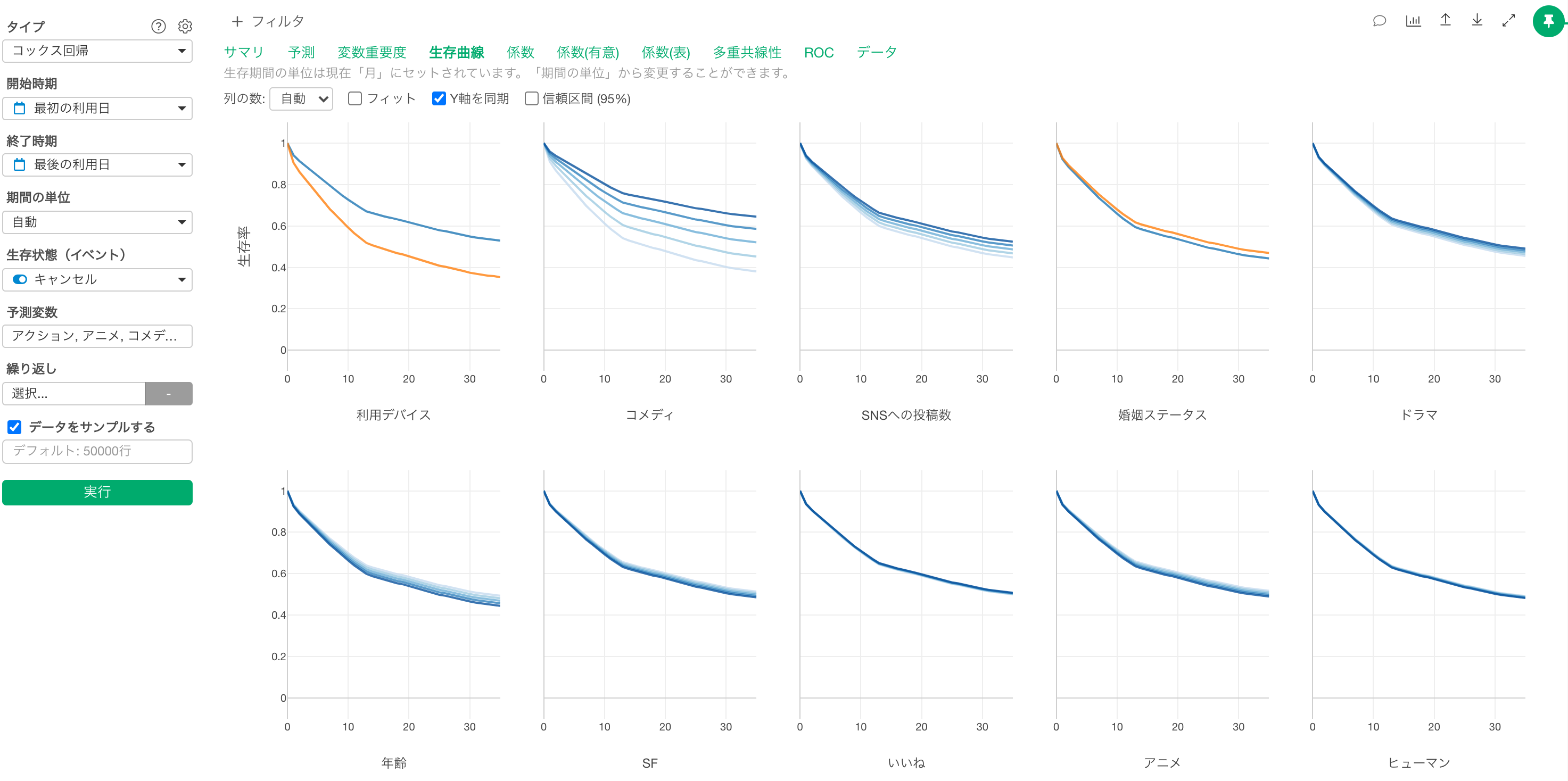
生存曲線
生存曲線タブでは、予測される生存曲線が予測変数によってどう変化するのかがわかります。
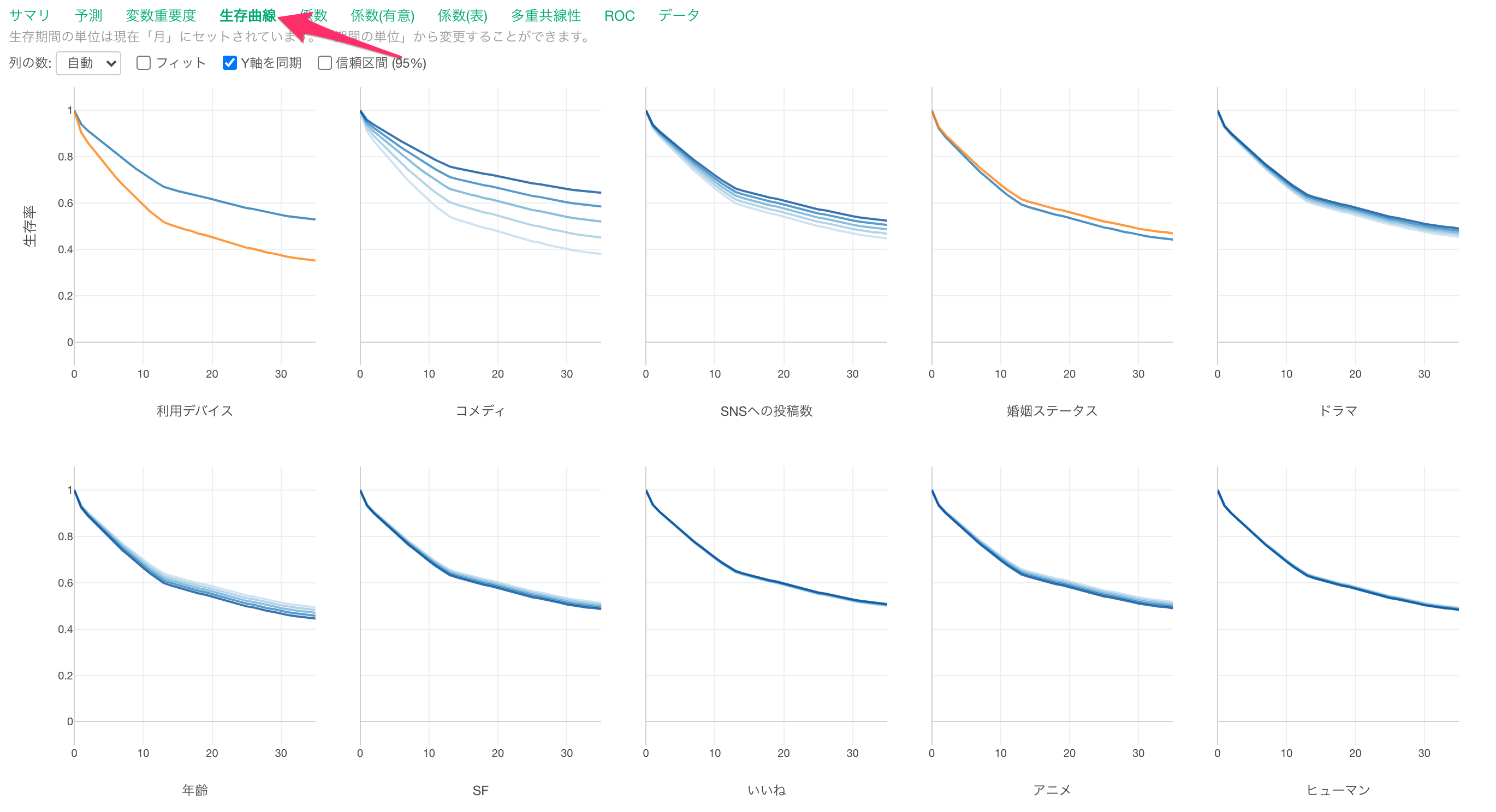
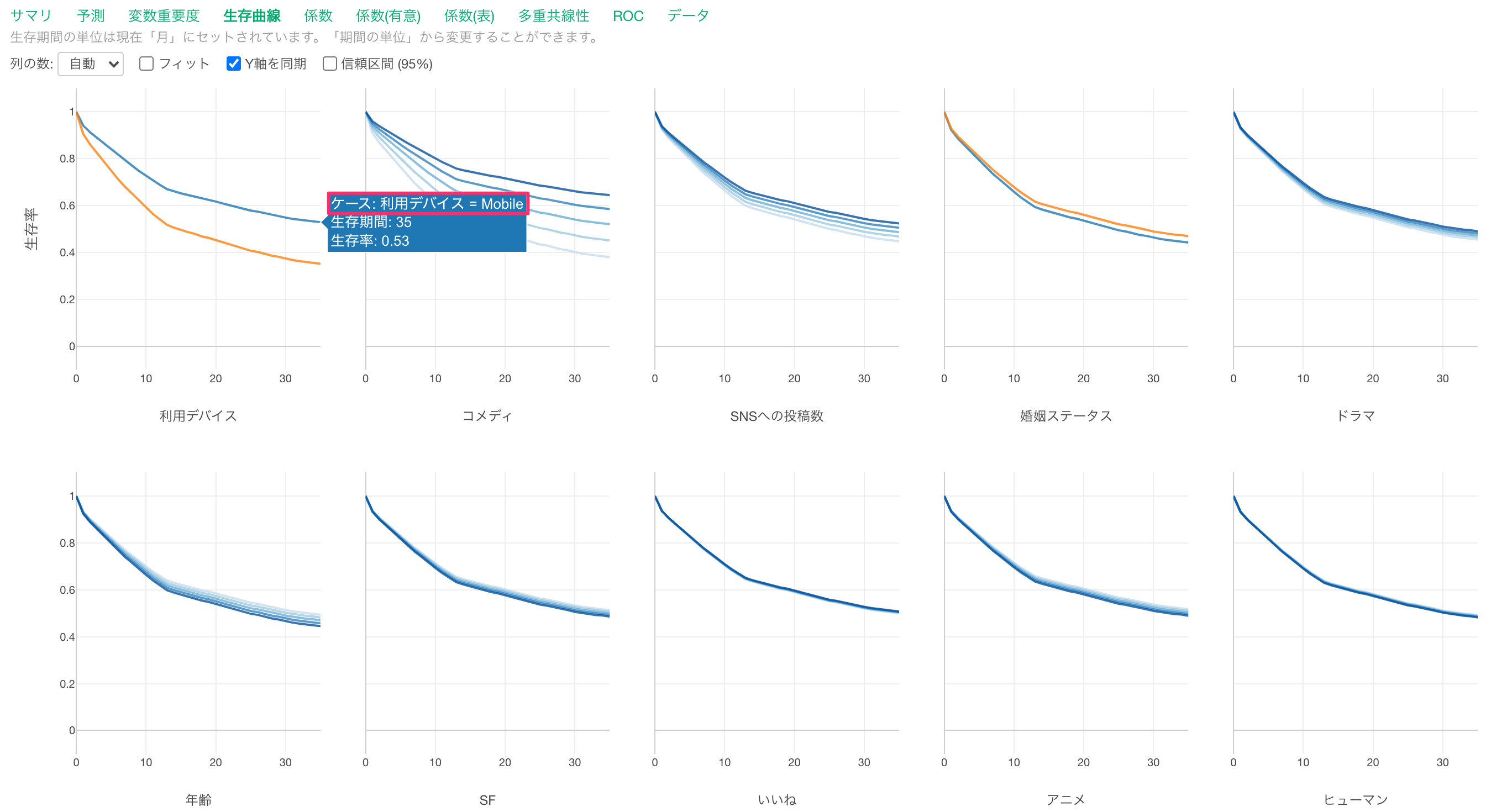
利用デバイスがモバイルのときは、PCと比べて生存曲線が緩やかなため、キャンセルが発生しづらいことがわかります。
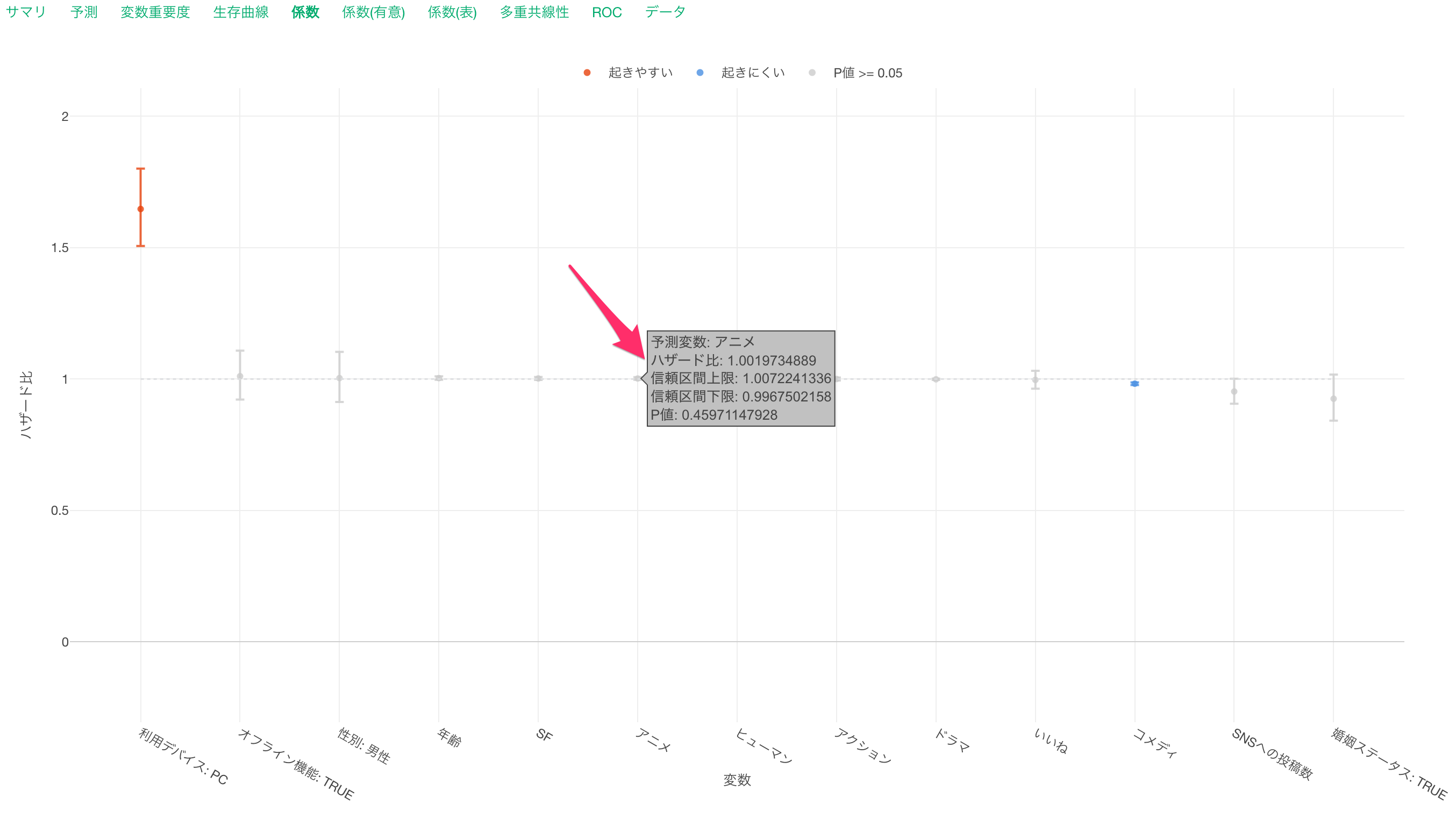
係数
係数タブでは、それぞれの変数のハザード比とその信頼区間や有意性がわかります。
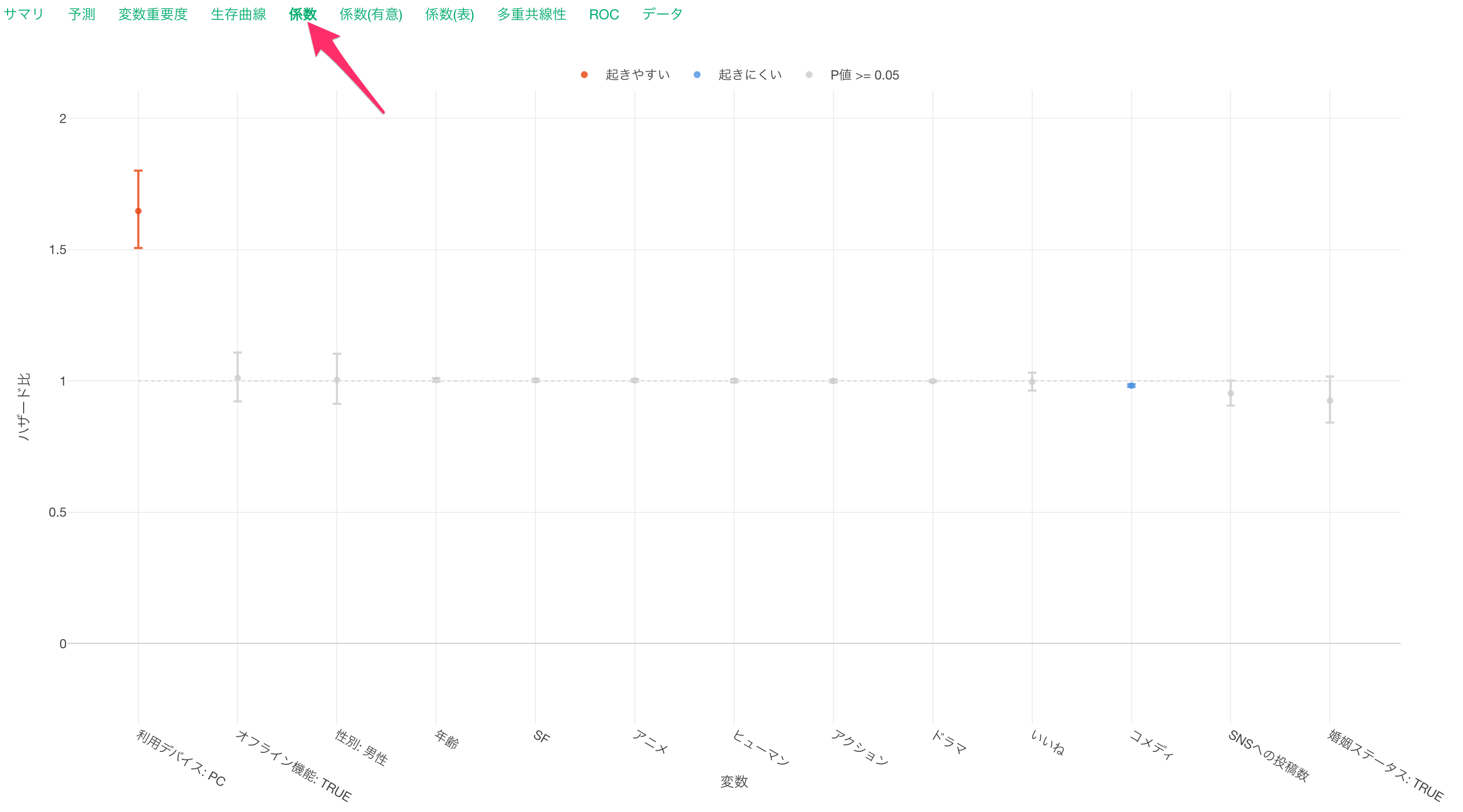
係数が、「起きやすい(赤)」または「起きにくい(青)」場合は、キャンセルとの関係が有意となり、P値は5%以下です。
これらの有意な変数はハザード比の信頼区間が1に重なっていない、つまりハザード比が1であることはないと言えます。
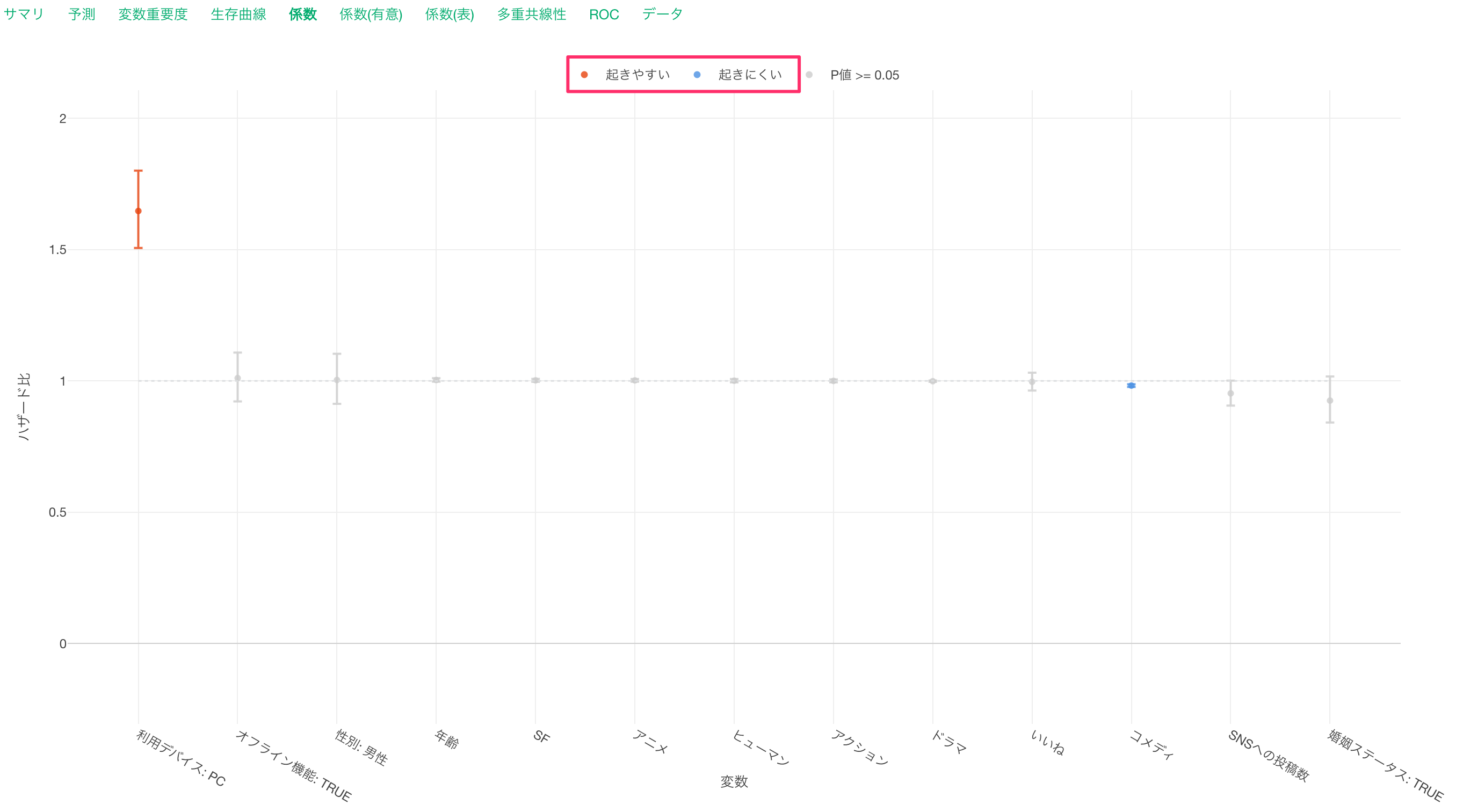
係数がグレーの変数はP値が基準値の5%以上で、統計的に有意であるとは言えない変数です。これらの変数は係数の信頼区間が1に重なっているため、ハザード比が1の可能性があります。
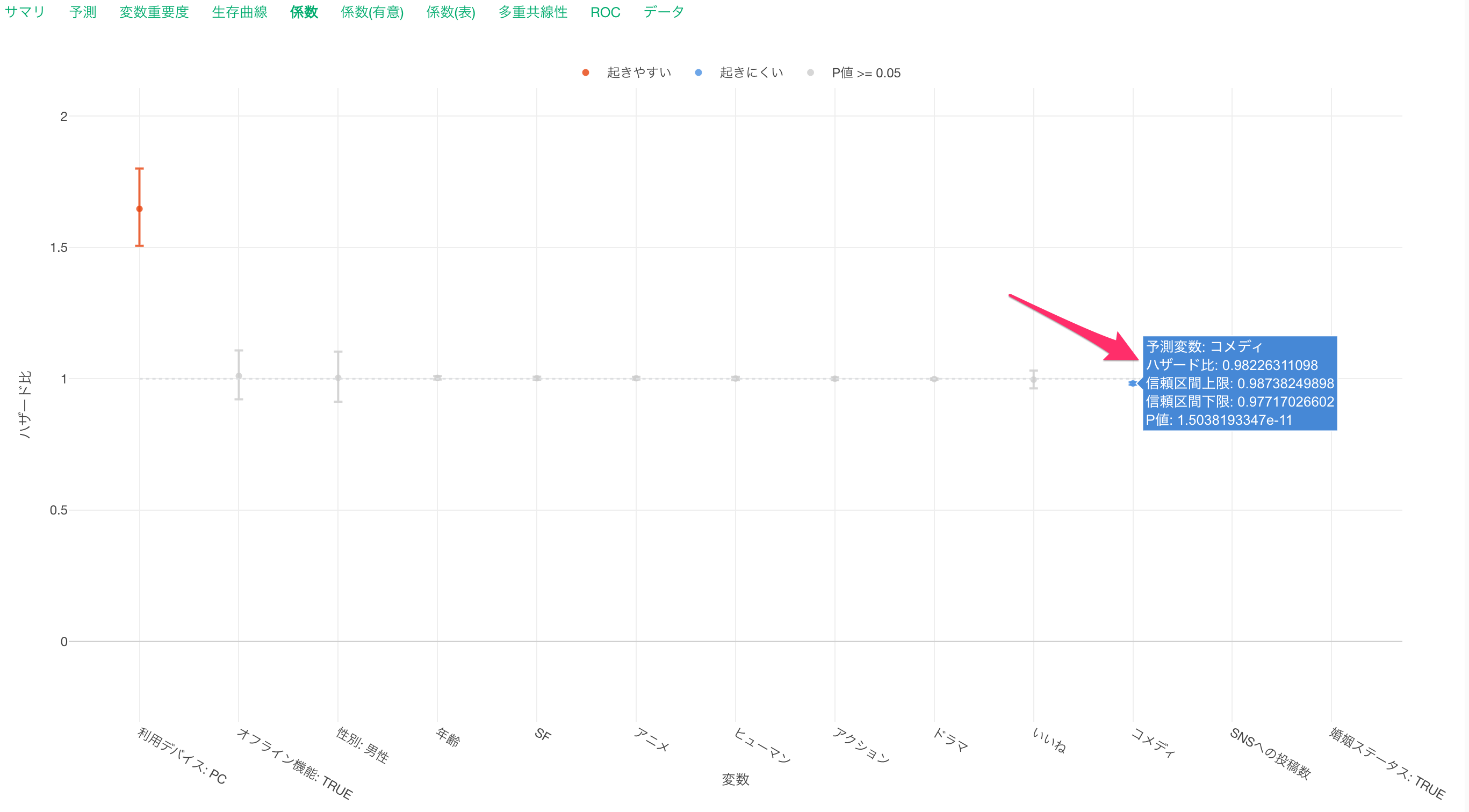
他の変数が一定だった時に、コメディ映画の視聴時間が1上がるとハザード(チャーンする可能性)が0.98倍になると期待されます。
この場合はチャーンしにくくなるという解釈になります。
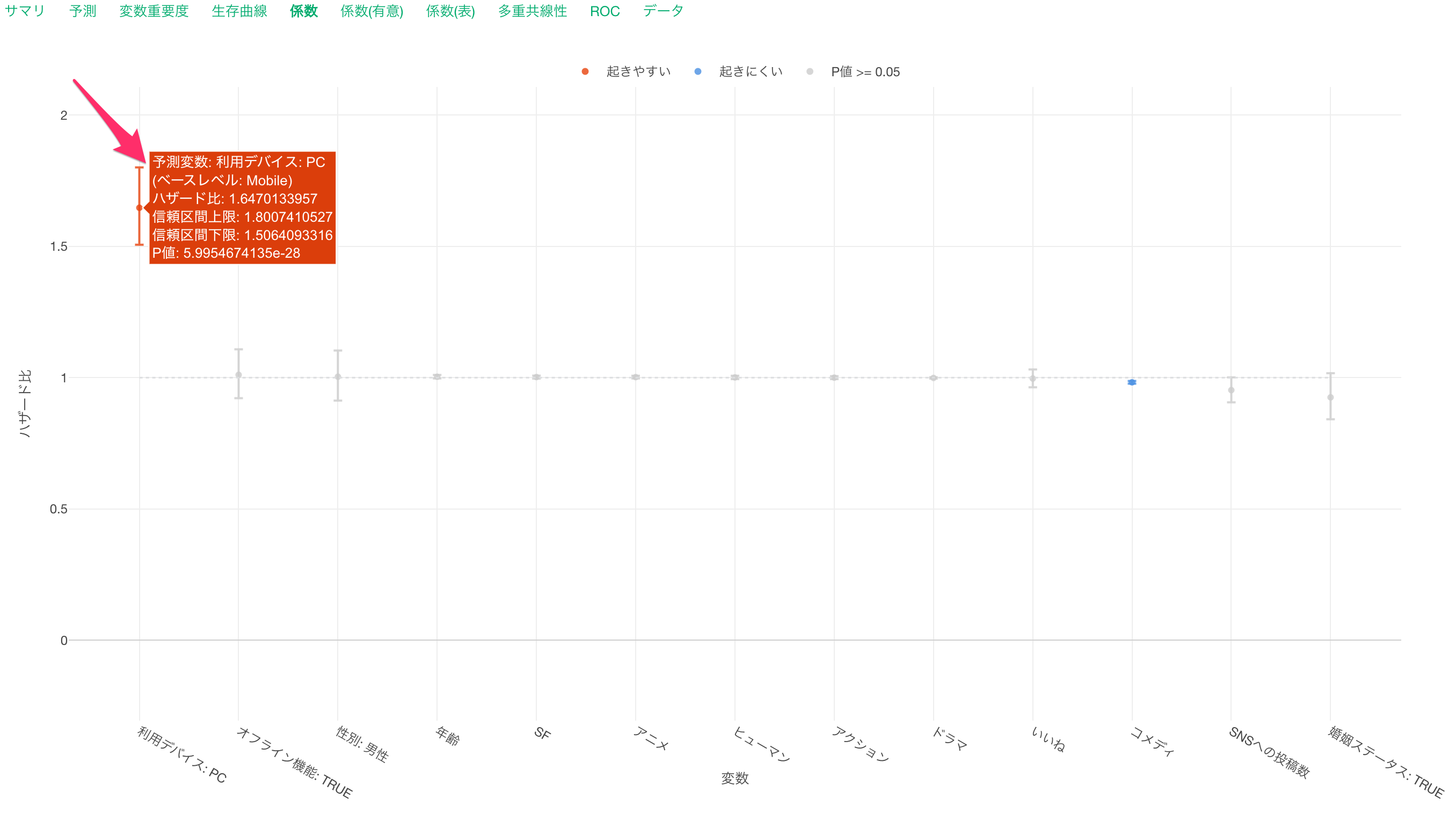
続いて、「利用デバイス: PC」に注目します。他の変数が一定だった時に、利用デバイスが「ベースレベル」のため、「Mobile」から「PC」になるとハザード(キャンセルする可能性)が1.64倍になると期待されます。
アニメの視聴時間に注目します。
すると、他の変数が一定だった時に、アニメの視聴時間が1上がるとハザード(キャンセルする可能性)が1.007倍になると期待されます。ただし、アニメの視聴時間の信頼区間は1をまたいでおり、P値も45%(0.45)と高いためキャンセルに関係があるとは言いきれません。
サマリ
サマリタブでは、この予測モデルの評価を確認できます。

時点AUCは、ある時点におけるキャンセルのTRUE/FALSEをこのモデルでどれだけ上手く分けられているかの指標で、0.5から1の間の値を取ります。1に近ければ近いほど、モデルがデータのTRUE/FALSEを上手く分けられていることを示します。

今回は、AUCが0.60と1に近くはないため、このモデルはTRUEとFALSEを、そこまで上手く分けられていません。
一致係数は、データの各観察対象に対して、イベントの起きやすさ(キャンセルの確率)をモデルで予測して、イベントが起きやすいと予測される順に観察対象を並べます。この観察対象の実際にイベントが起きた順番を比較して、どれほど一致しているかを数値化したもので、0から1の間の値を取ります。
一致係数の値が1に近いほど、モデルで予測した結果と実際のイベントが起きた順番が一致していることを示します。

今回は、一致係数が0.59と1に近くはないため、このモデルによって予測された結果と実際のデータでのイベントの発生順はあまり一致していないことになります。
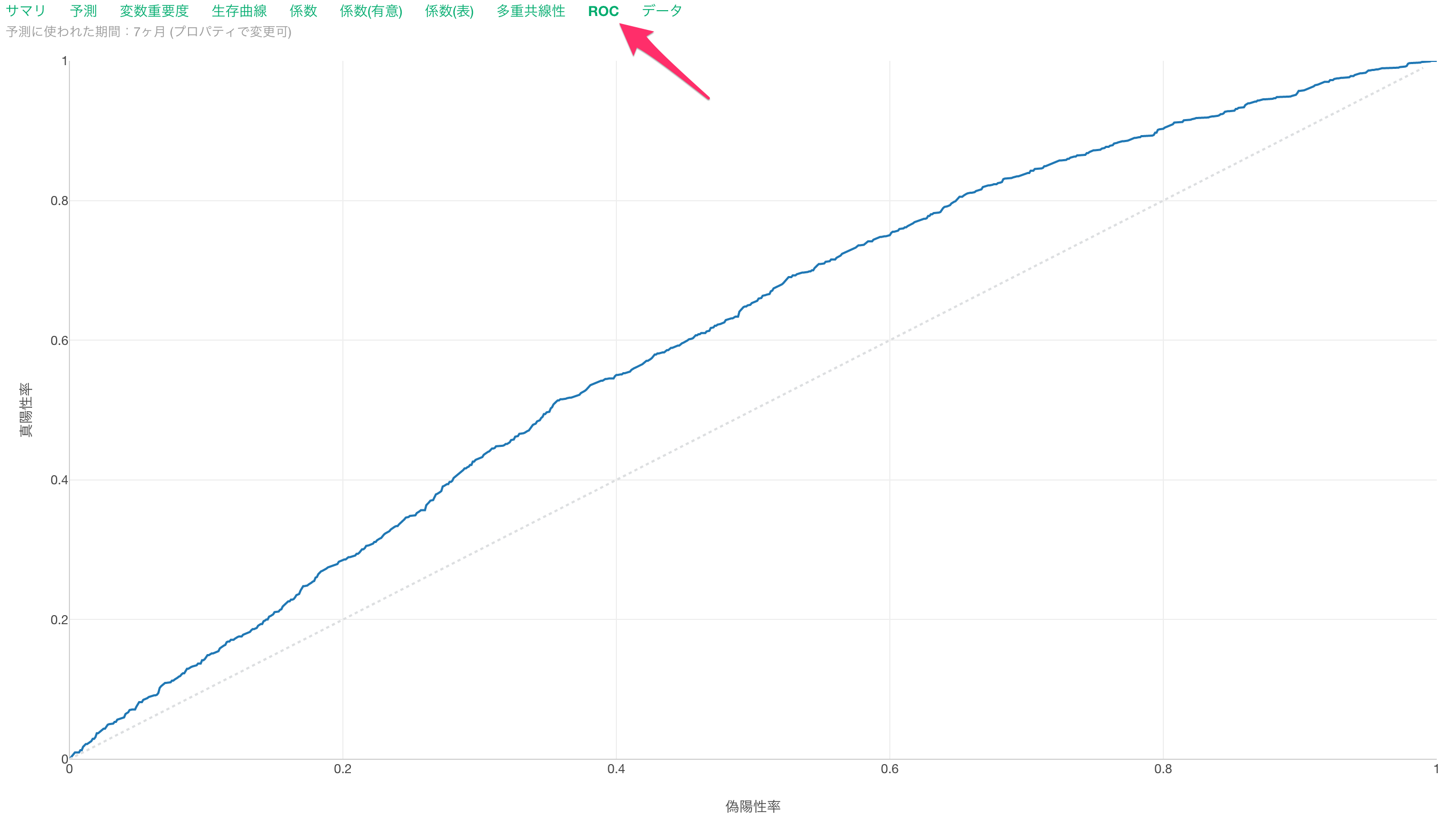
ROC
ROCタブでは、時点AUCの元となる面積をROC曲線から確認できます。
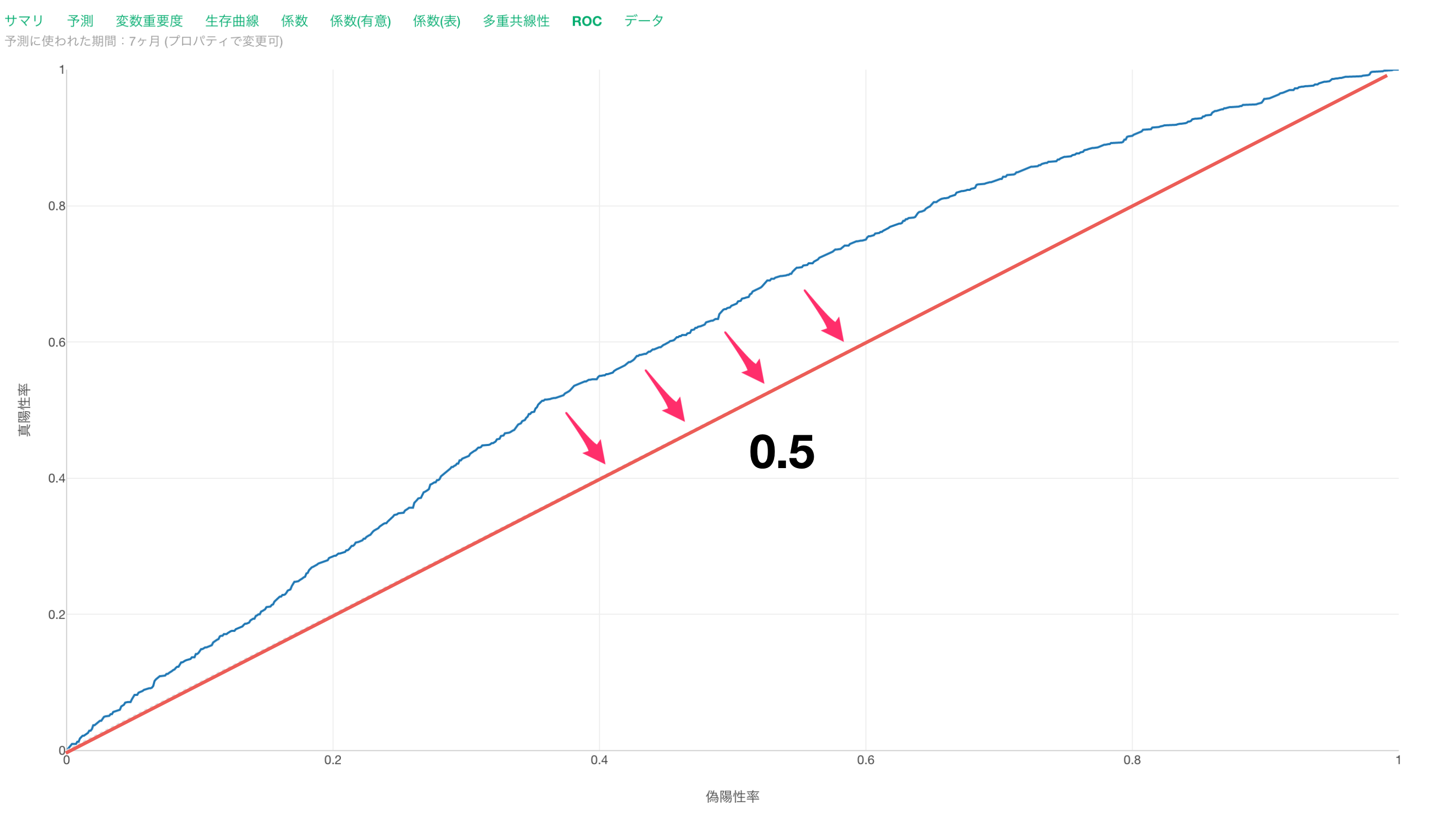
時点AUCが低い時はROC曲線が対角線上に近づいていきます。
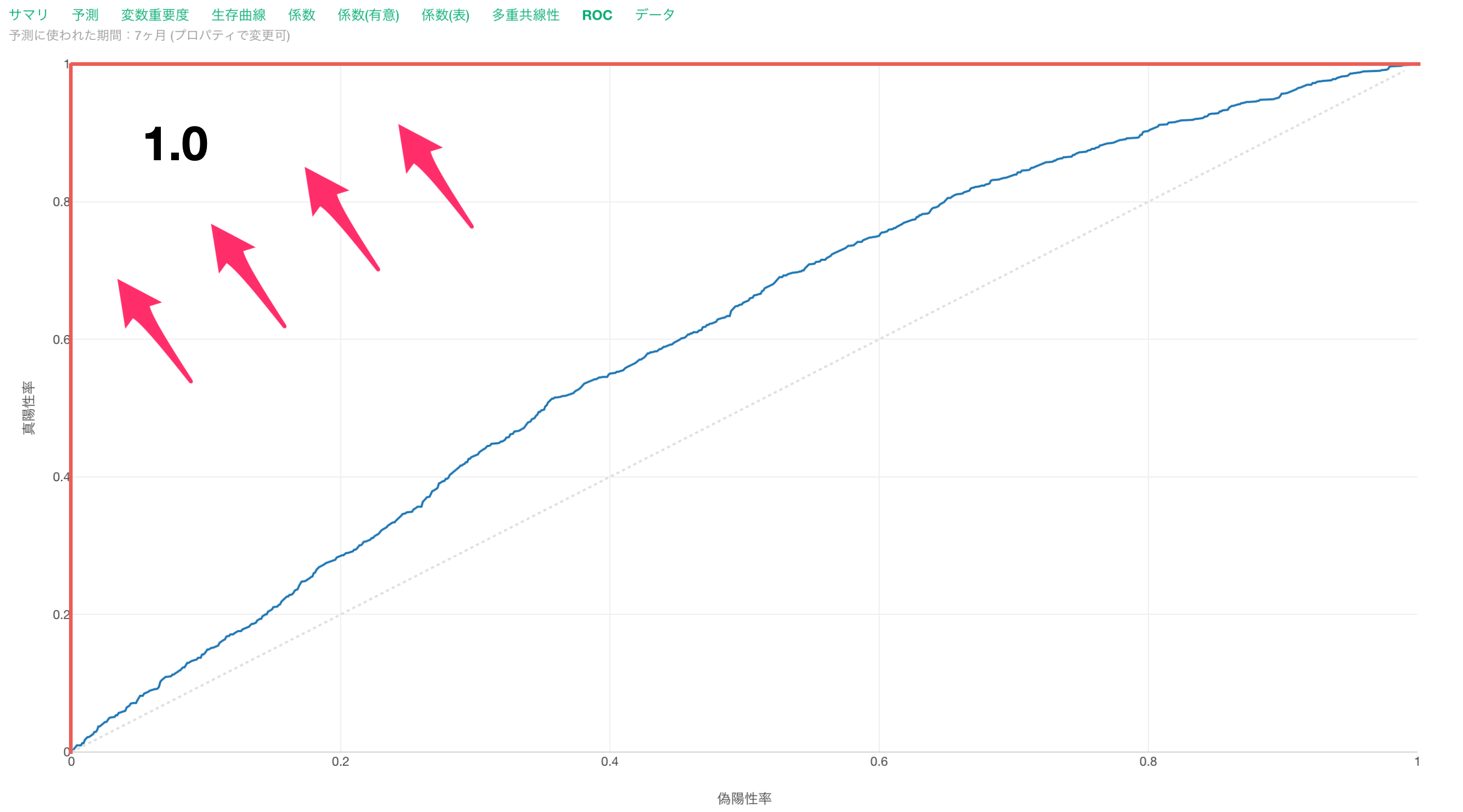
時点AUCが高い時はROC曲線が直角に近づいていきます。
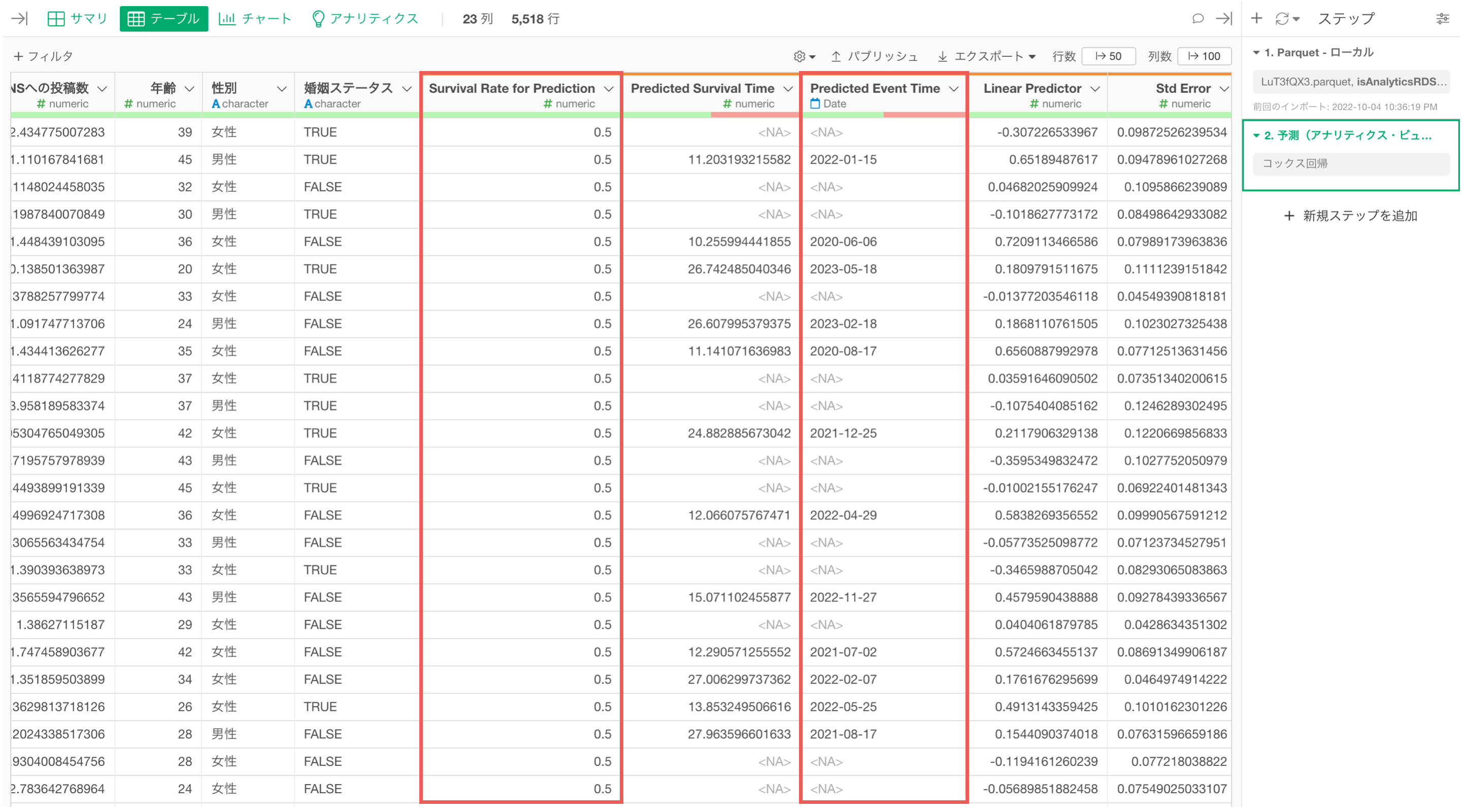
データ
データタブでは、モデルに使用したデータと予測値をテーブル形式で表示されます。
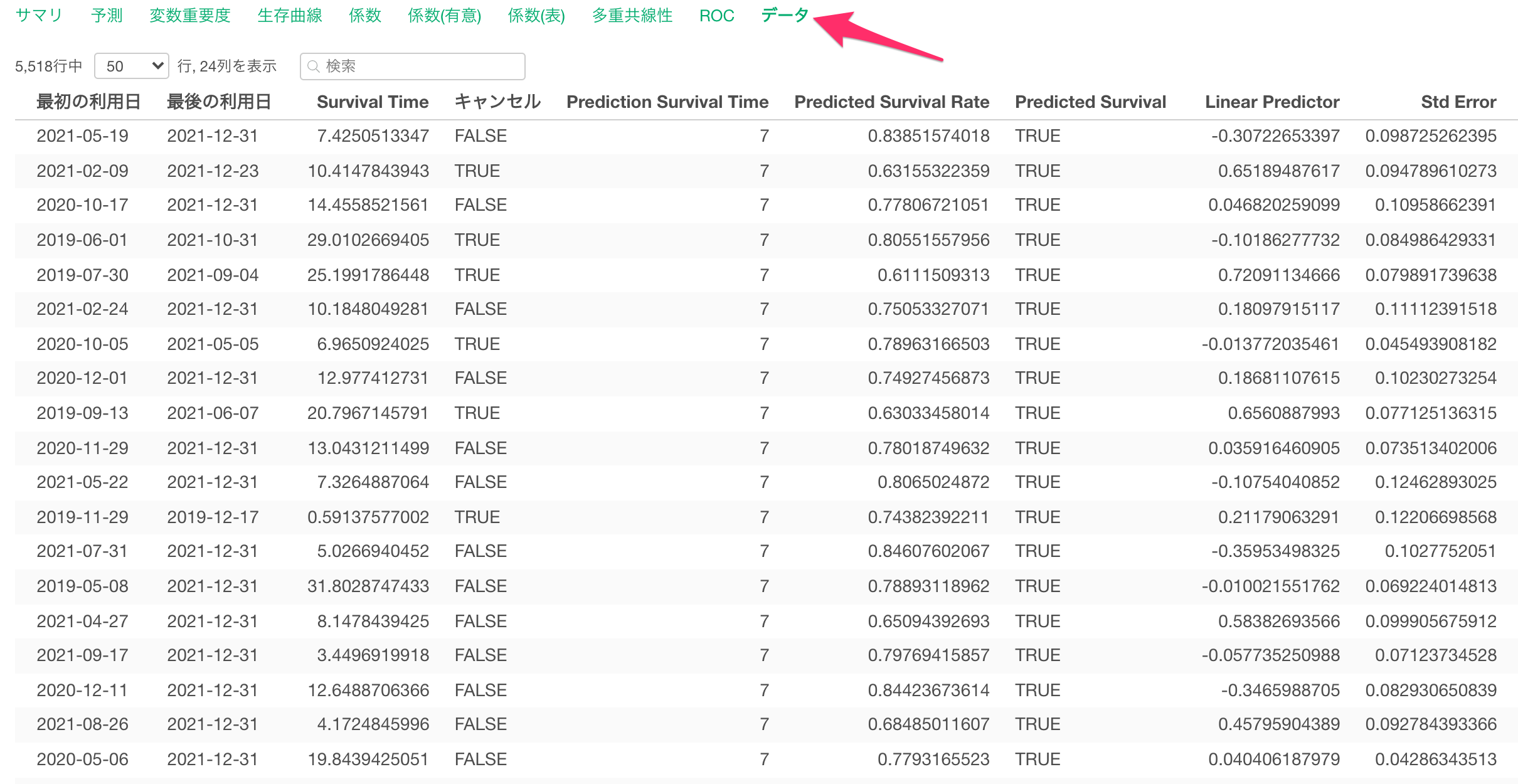
「Survival Time」は各観察対象(顧客)の生存期間を表しており、各観察対象の生存状態(キャンセル)も確認できます。
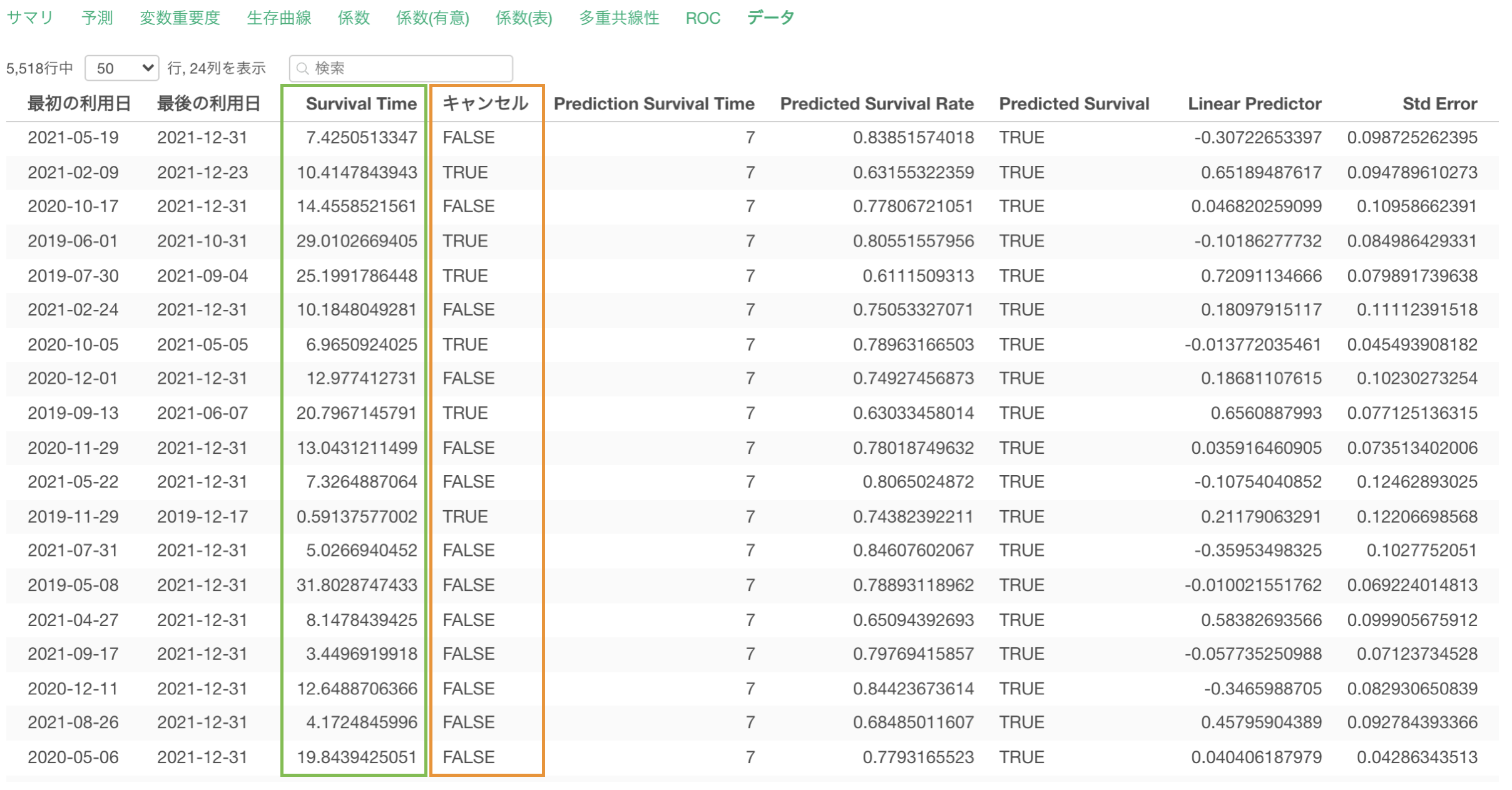
「Survival Time for Prediction」はどの時点での生存確率を予測しているかの情報です。(デフォルトでは観察対象の生存期間の平均値が利用されます。)
また、「Predicted Survival Rate」は、「Survival Time for Prediction」で設定した期間における生存確率を表していて、「Predicted Survival」は「Predicted Survival Rate」に対して設定したしきい値を元にした生存状態の予測結果です。
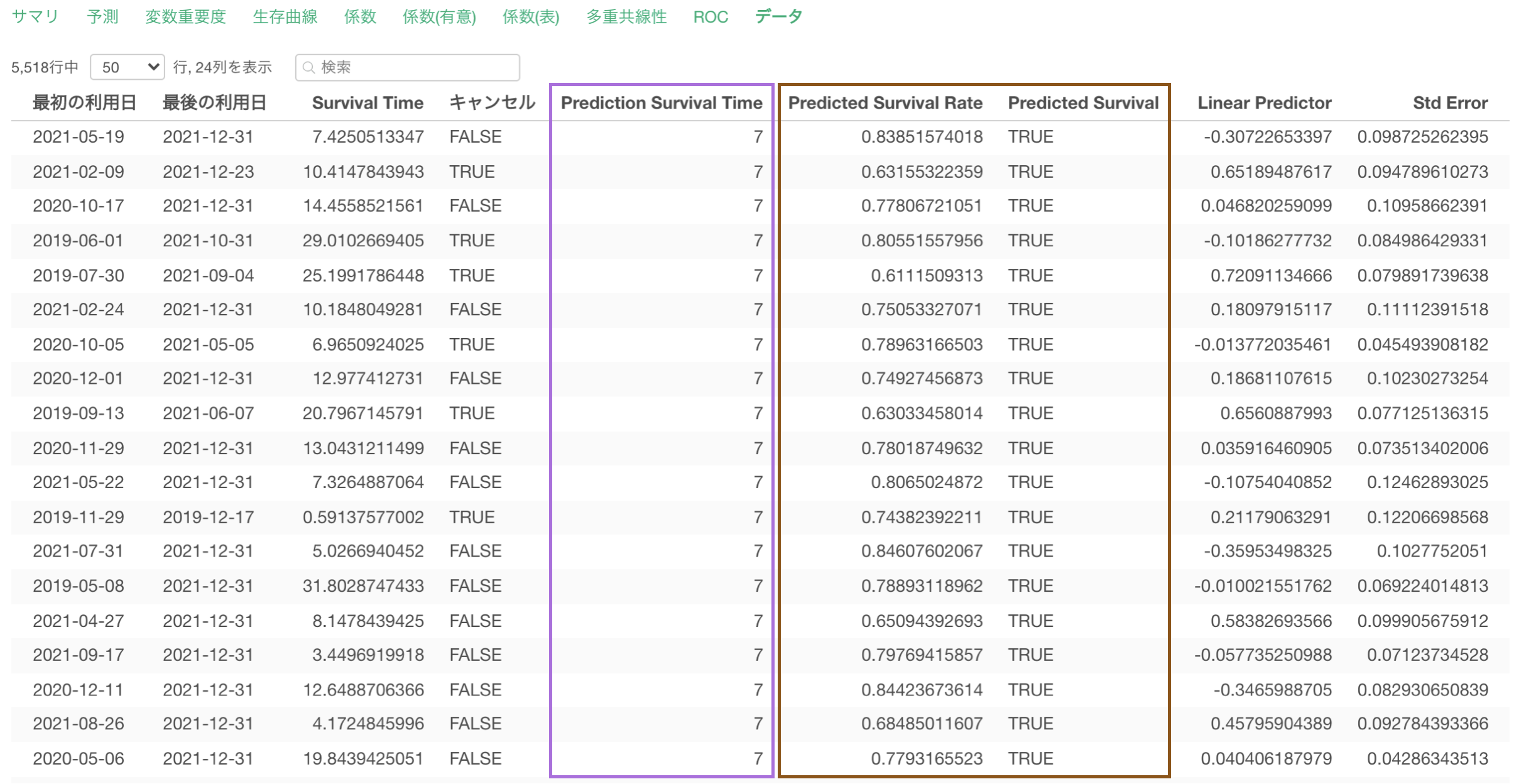
Nヶ月後の生存率の予測
作成したコックス回帰のモデルを使うと、今日を起点にしたときに「1カ月後の各観察対象(例: 顧客)の生存確率」を予測できます。
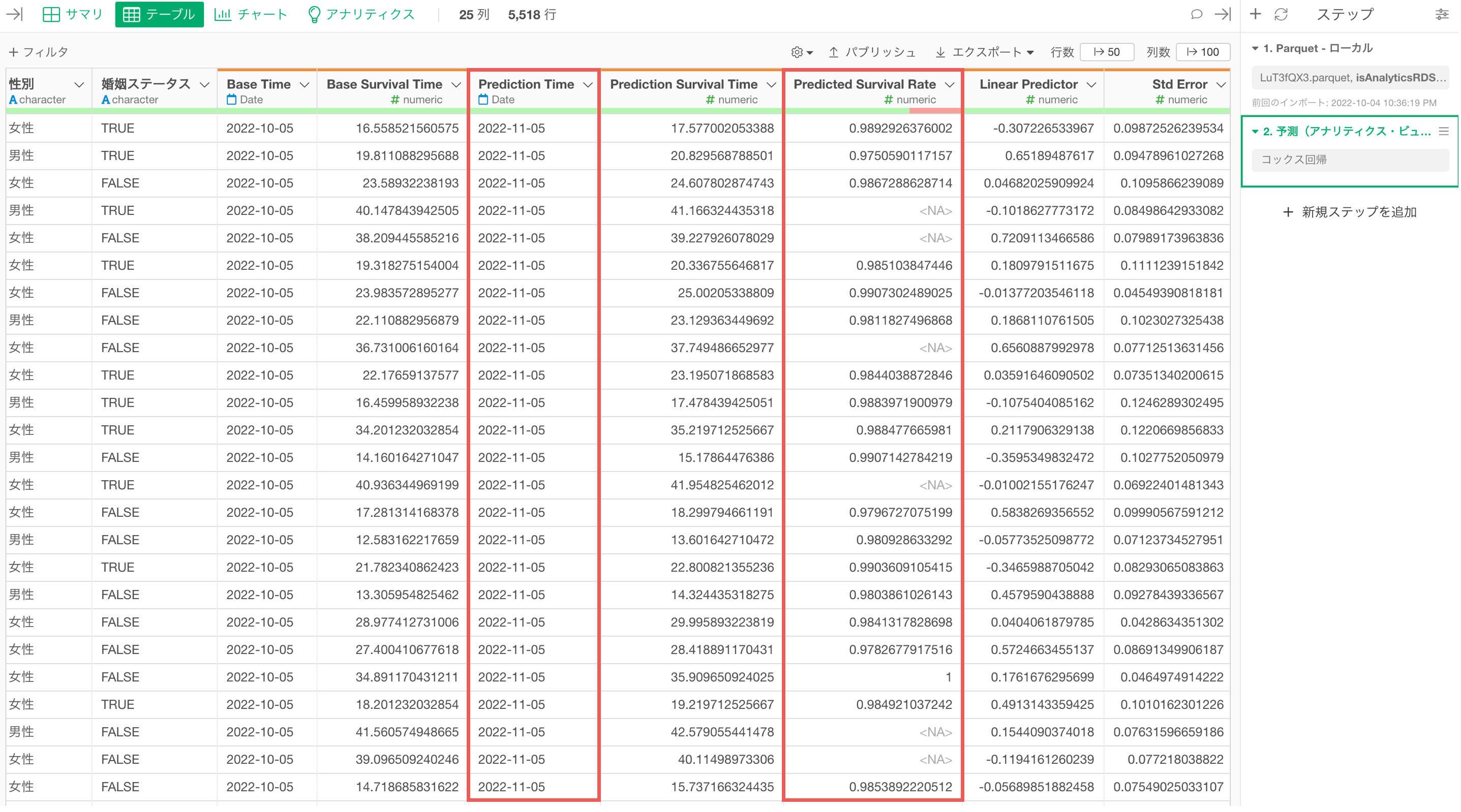
特定の生存率になる日付の予測
また、各観察対象(例: 顧客)の生存確率が50%になる「日付」も予測できます。
参考資料
コックス回帰に関する参考資料は下記をご覧ください。
コックス回帰に関するよくある質問
Q: 予測タブで表示されている実測値はどのように求められているのですか?
予測タブの実測値はそれぞれの予測変数のデータタイプによって表示が異なります。 詳しくはこちらのノートをご覧ください。
Q: 予測タブで表示されている予測値はどのように求められているのですか?
予測値のチャートはPartial Dependence Plot(PDP)と呼ばれるもので、注目している変数の値を変化させたときに、予測結果がどう変わるかを可視化したチャートとなります。詳しくはこちらのノートをご覧ください。
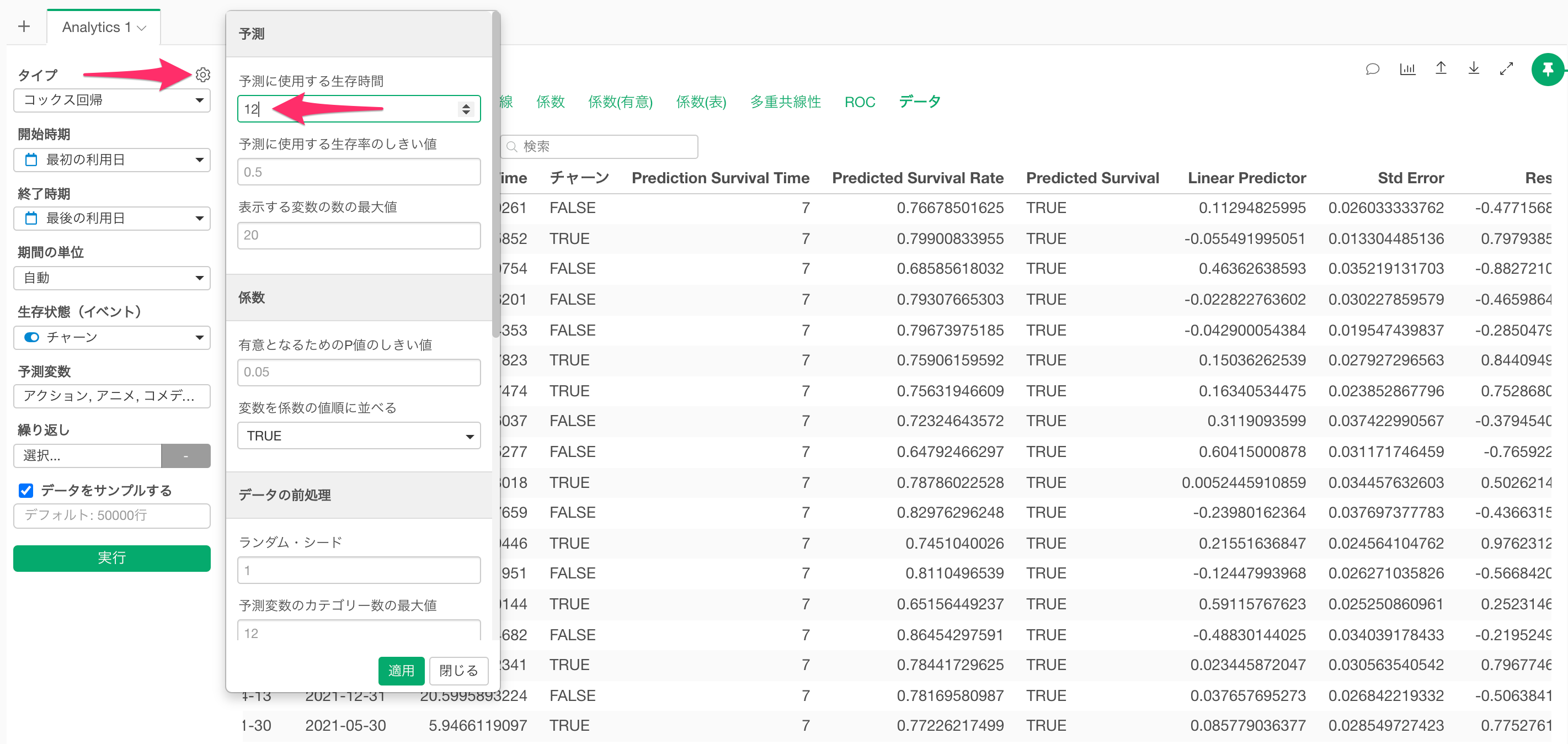
Q: 予測に使用する生存期間はどのように変更できますか?
「予測に使用する生存期間」のデフォルト値は観察対象の生存期間の平均値ですが、プロパティの「予測に使用する生存期間」から変更できます。
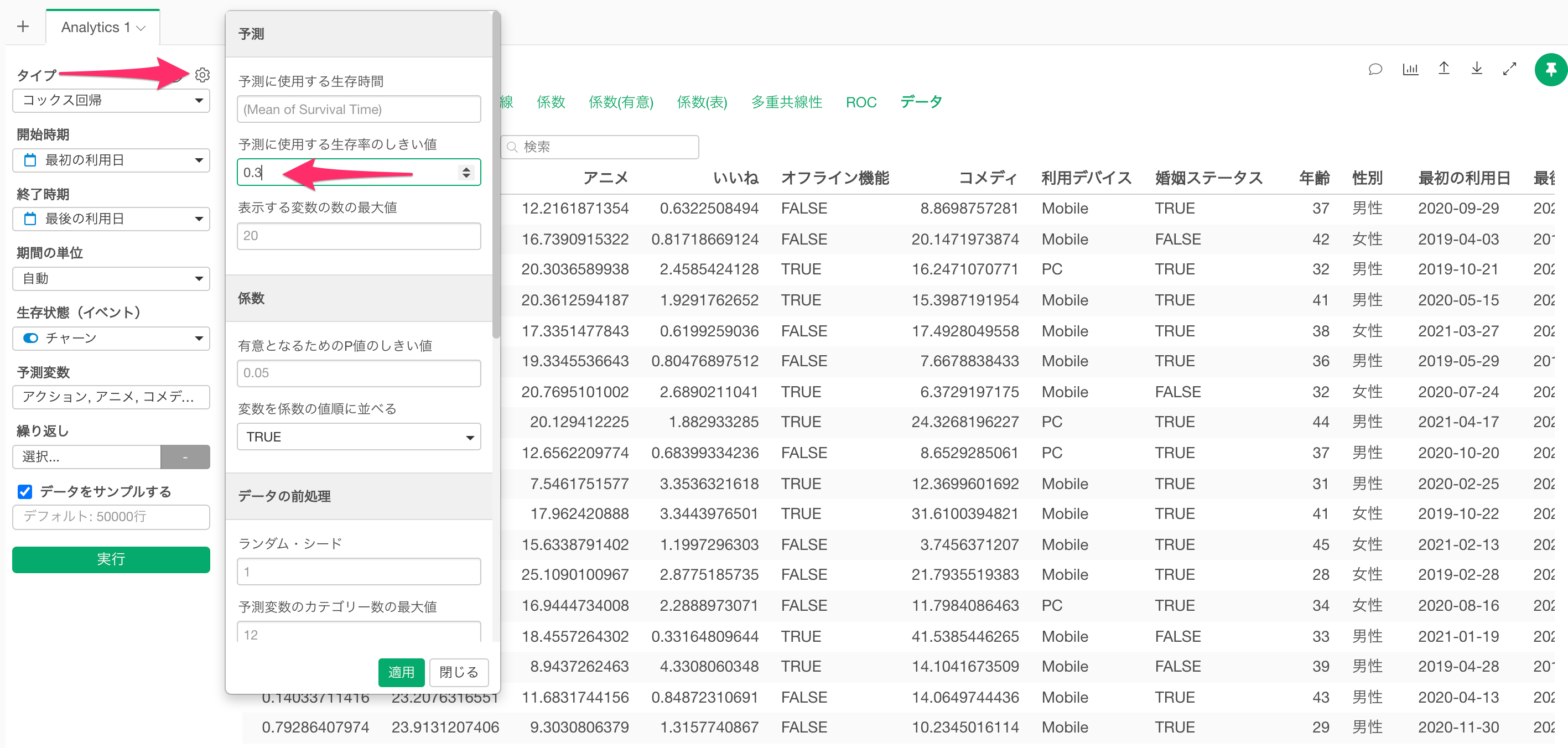
Q: 予測使用する生存率のしきい値はどのように変更できますか?
プロパティの「予測に使用する生存率のしきい値」から変更できます。しきい値のデフォルトは0.5になっており、0.5以上の場合はTRUEと予測し、0.5よりも小さい場合はFALSEと予測します。
Q: 時点AUCと一致係数はどちらを優先してみればいいでしょうか?
決まりのようなものはないのですが、予測において、何を重視したいかによってどの指標を重視するかを決めていただければよいかと思います。
例えば、一年後のように、特定の時点までにイベントが発生するのかどうかを予測することが重要であれば、1年後の「時点AUC」を見ていただくのがよいと思います。
どの時点ということに関係なく、イベントが発生しやすそうなほうから観察対象(例:顧客、従業員、など)にランク付けすることが重要なのであれば、「一致係数」をみていただくのがよいと思います。