因子分析・主成分分析における回転とは？

因子分析や主成分分析では、データから潜在的な要因（因子）を見つけ出します。しかし、最初に計算された因子は必ずしも解釈しやすいものではありません。そこで、回転という手法を使って、因子をより解釈しやすい形に変換します。

回転には大きく分けて2つのタイプがあります：

• 直交回転：因子同士が完全に独立（無相関）

• 斜交回転：因子同士に相関を許す

例えば、学力テストのデータを分析して「数学的能力」と「言語的能力」という2つの因子を見つけたとします。この2つの能力は実際には関連し合っている可能性があるため、回転方法の選択が重要になります。

軸の決め方の基本的な考え方

因子分析や主成分分析では、まずデータのばらつき（分散）を最大化する方向に軸（因子）を配置することから始まります。

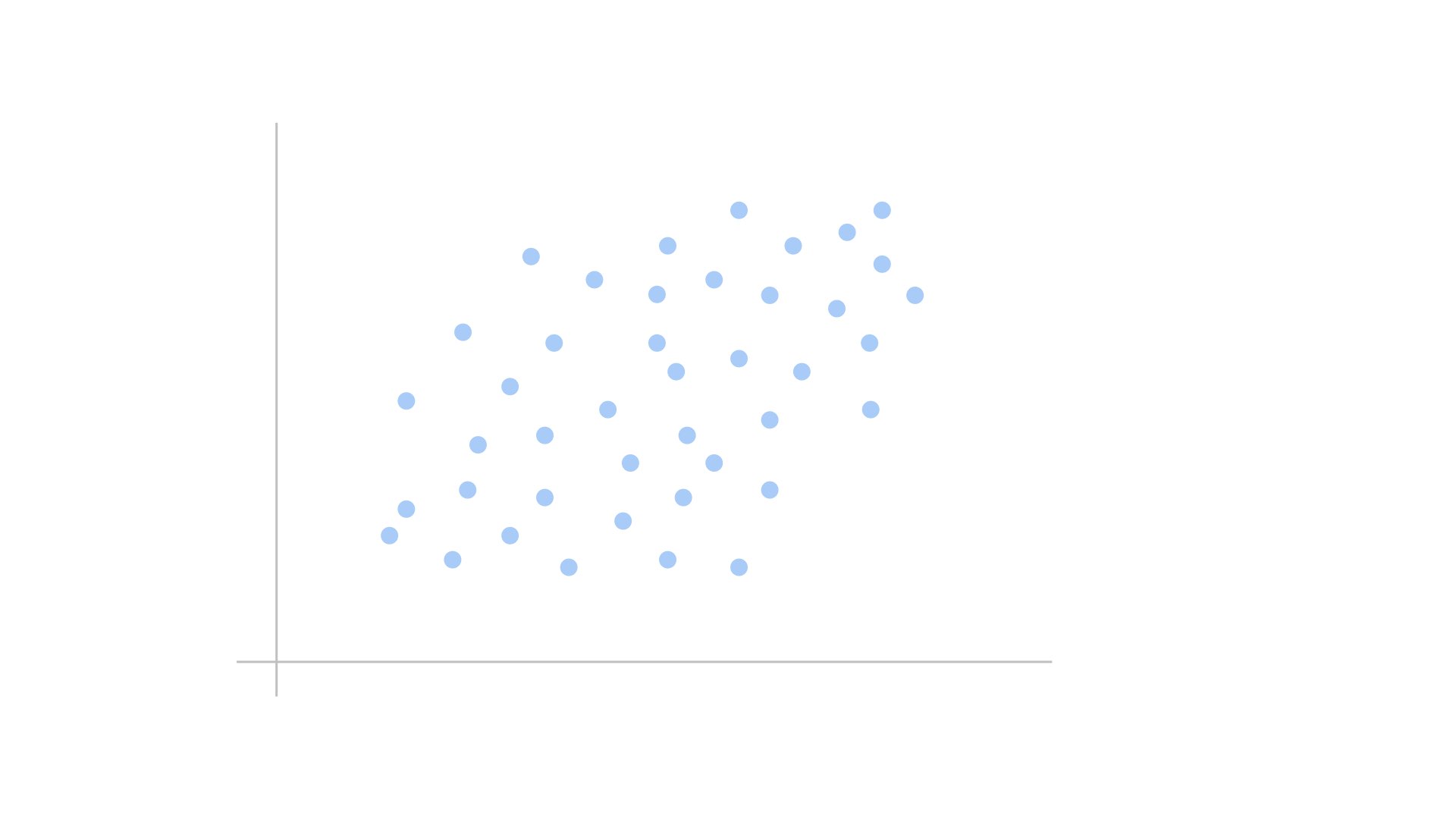
最初の状態では、データポイント（青い点）がランダムに散らばっています。

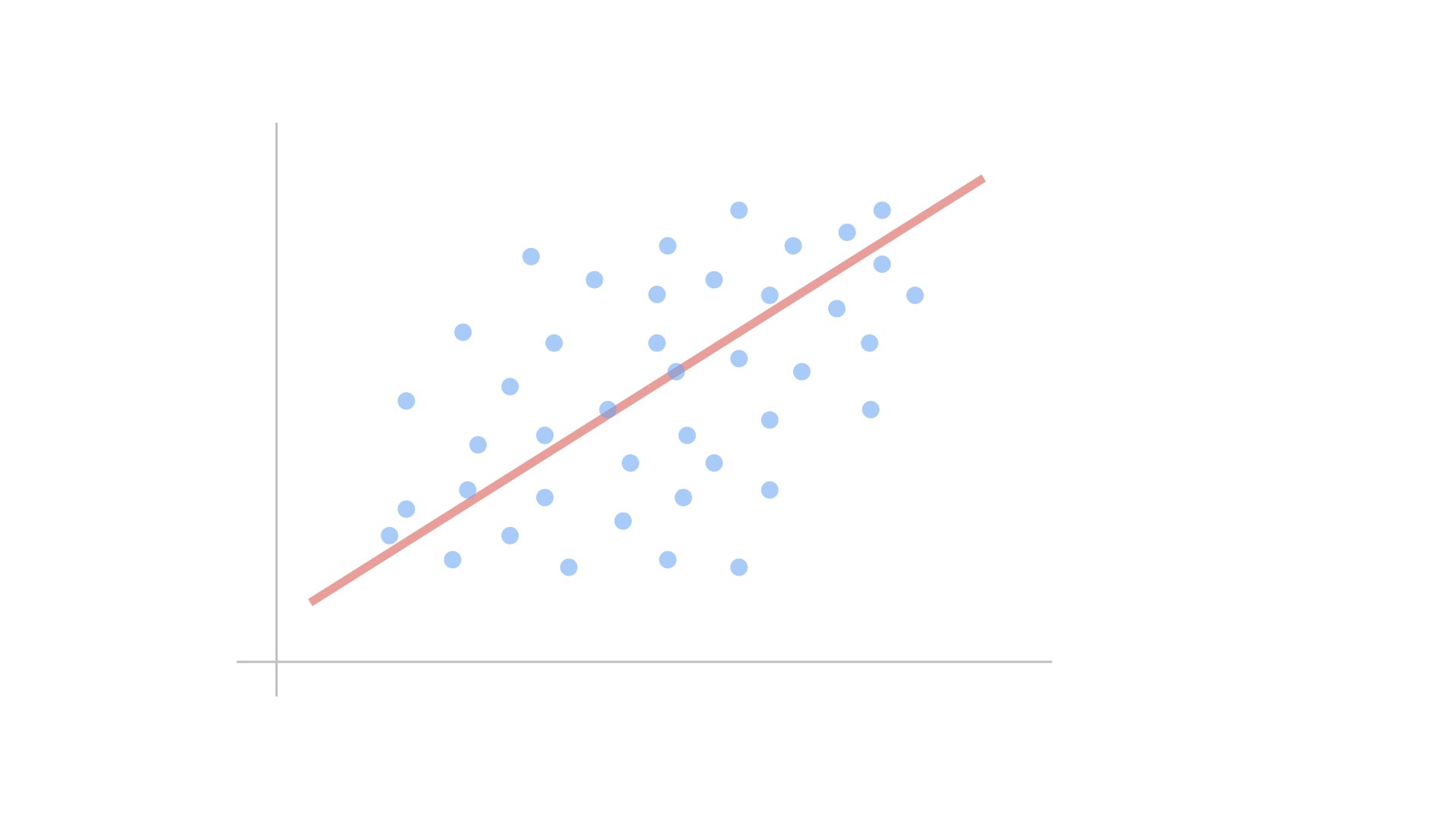
第1軸（赤い線）は、データのばらつきが最も大きくなる方向に引かれます。これにより、データの主要な変動パターンを捉えることができます。

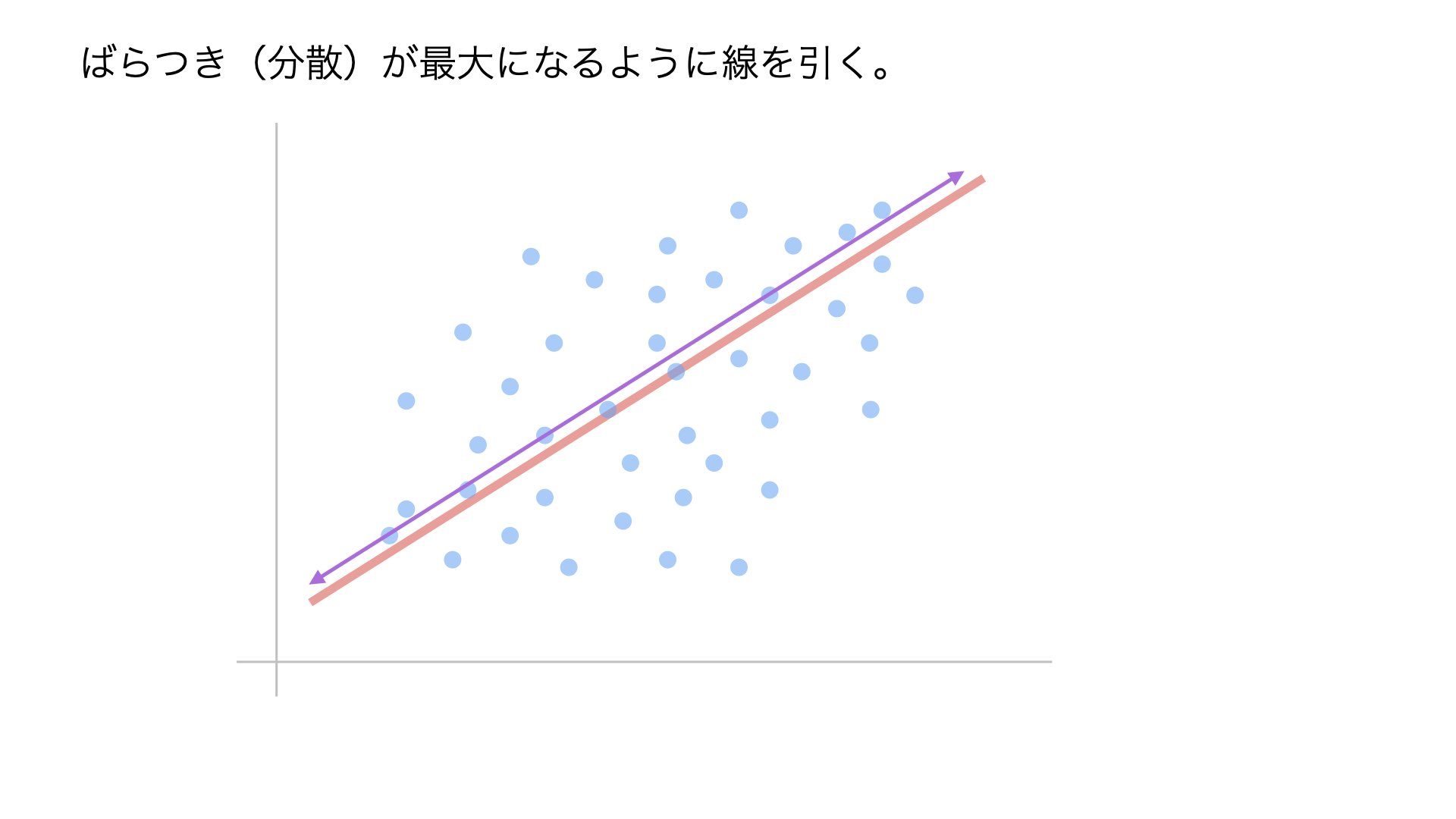
軸の決定方法は、データのばらつきが最大になるように線の方向を調整することです。紫色の矢印が示すように、様々な角度を試して最適な位置を探します。

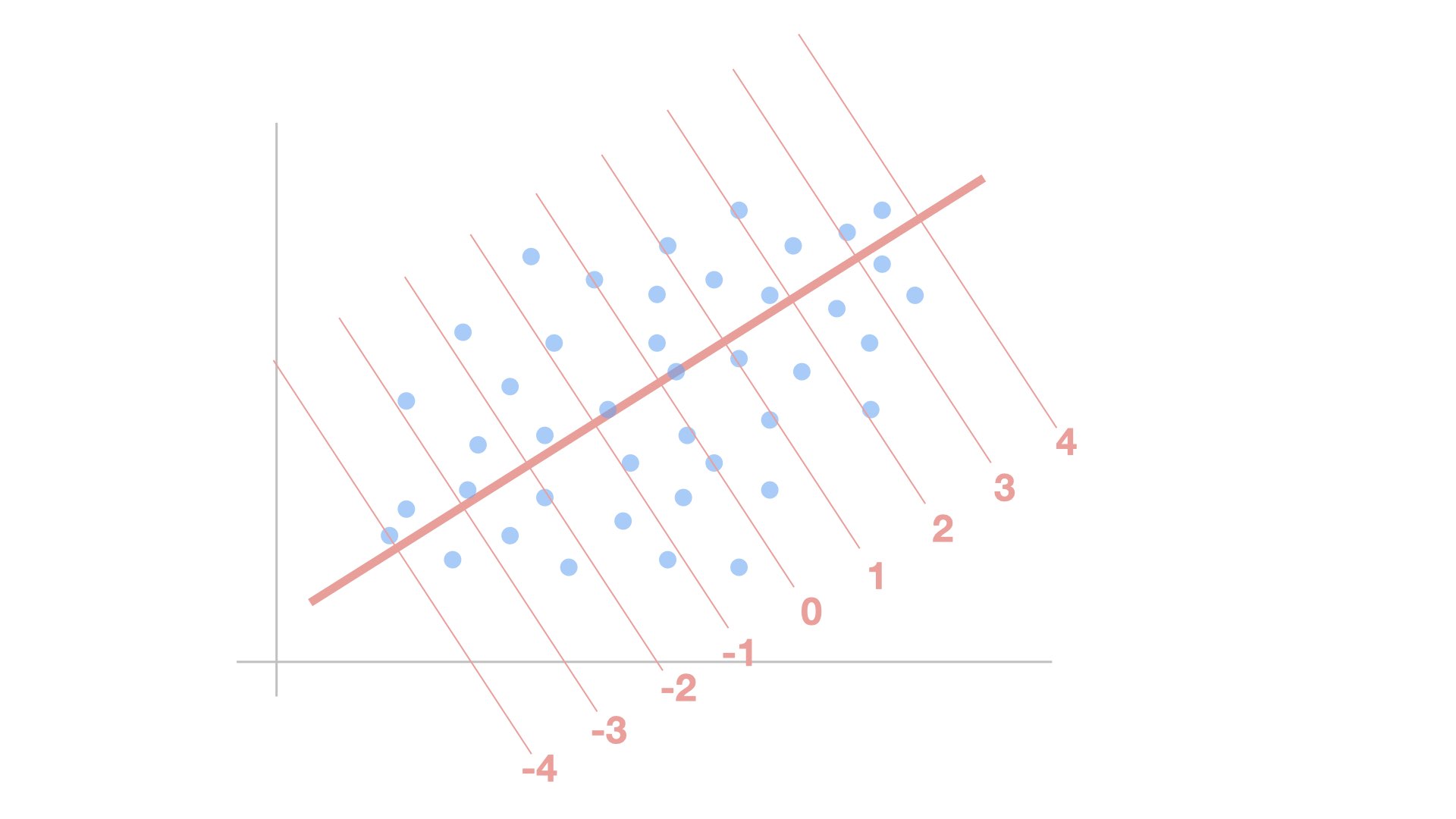
軸が決まったら、平行な線（等高線のような線）を引いて、各データポイントがどの「レベル」にあるかを数値化します。図では-4から4までの数値が振られています。これが因子得点となります。

直交回転

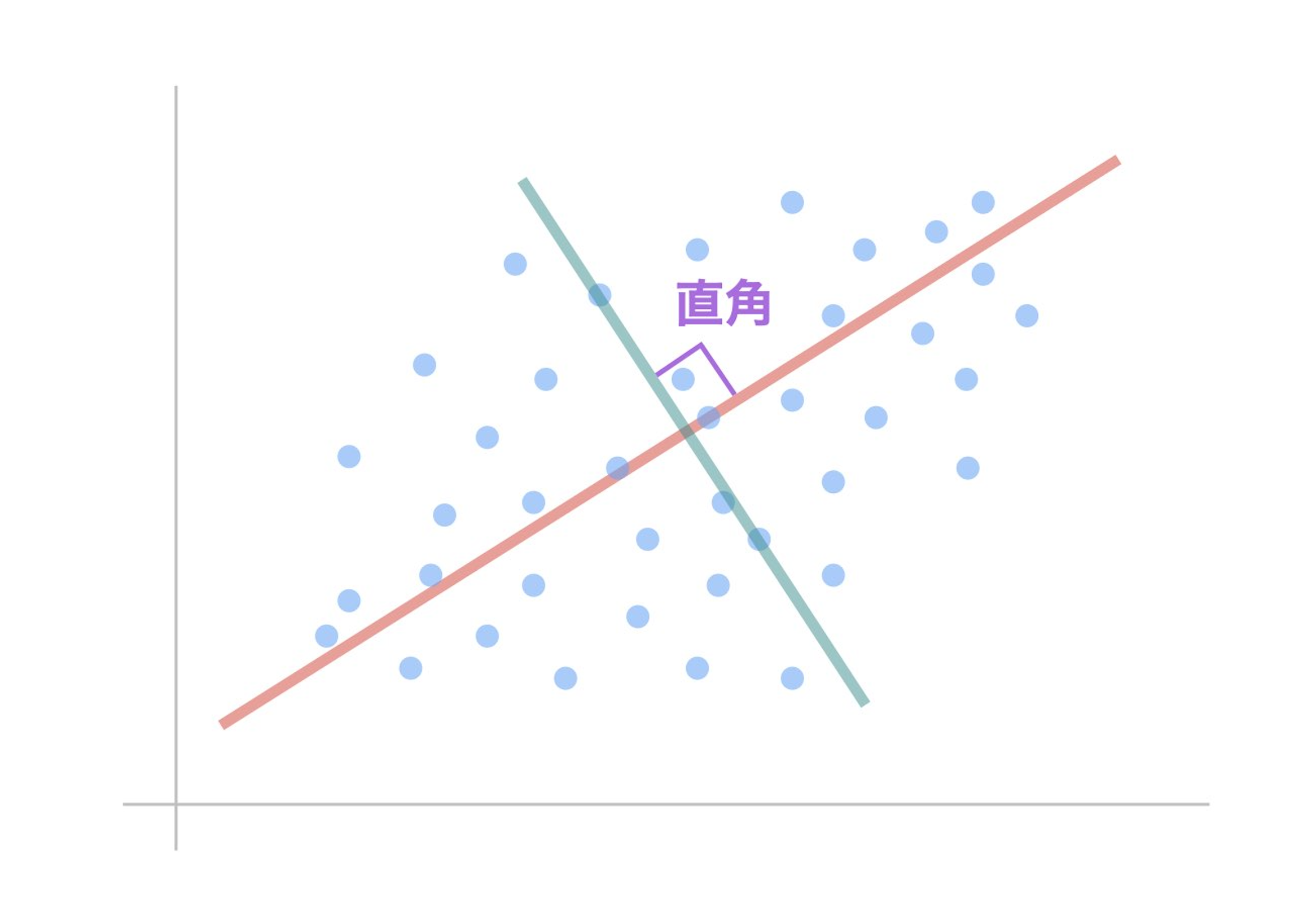
直交回転では、赤い線（第1因子）と青緑の線（第2因子）が常に直角を保ちます。「直角」と書かれた部分が90度の角度を示しています。

斜交回転

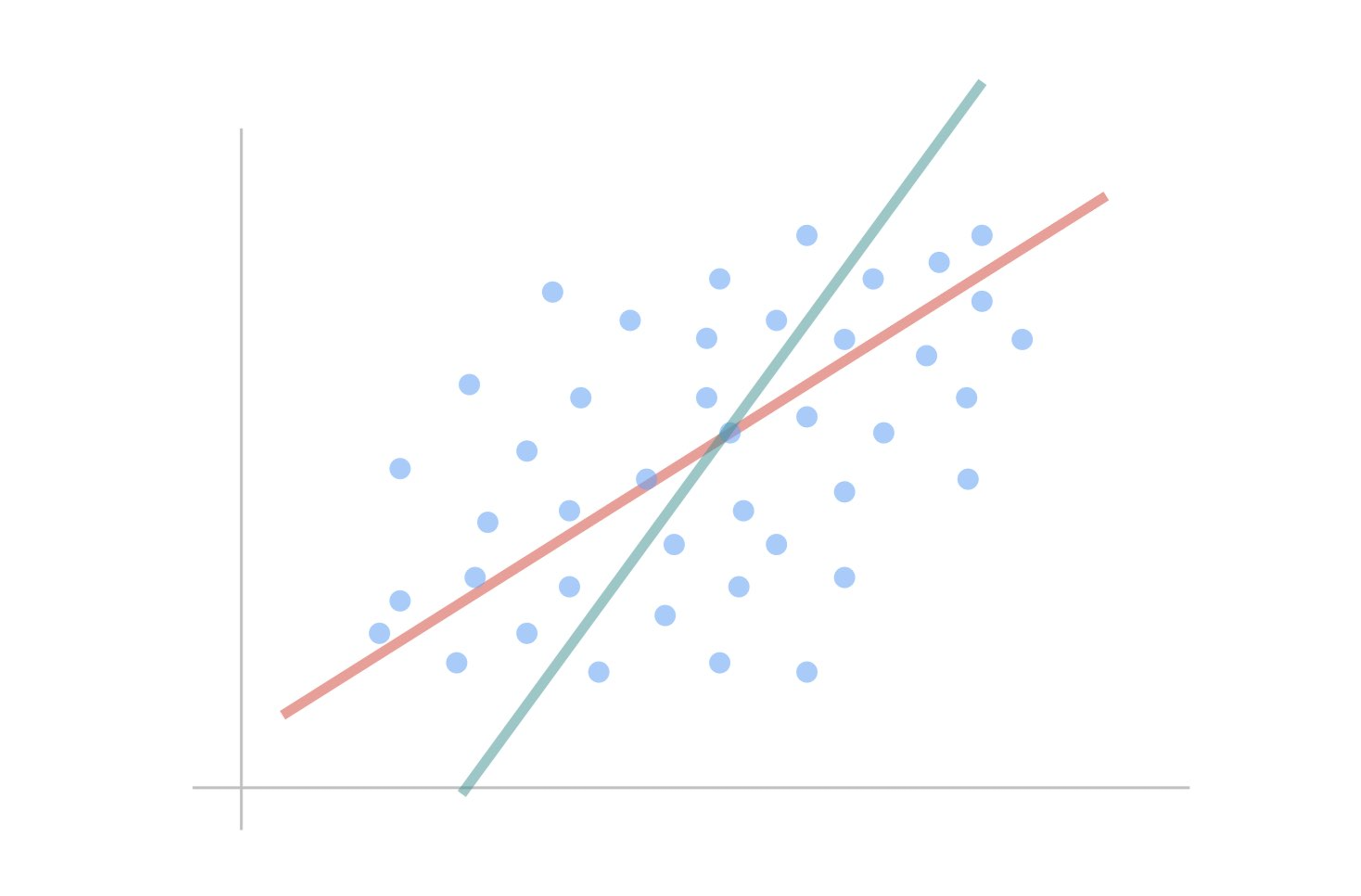
斜交回転では、2つの因子（赤い線と青緑の線）が直角以外の角度で交わります。これにより、因子間に相関が生まれることがあります。

2つの回転方法の比較

まとめ

回転方法の選択は、分析の目的と実際のデータの性質によって決まります。

直交回転を選ぶべき場合：

• 因子を独立した概念として扱いたい

• シンプルで理解しやすい結果が欲しい

• 因子間の相関を考慮する必要がない

斜交回転を選ぶべき場合：

• 因子間に関係があることが予想される

• より現実的なモデルを構築したい

• 因子間の相関も分析対象として重要