一般化線形モデル - GLM - 二項分布の使い方
一般化線形モデル(GLM)の二項分布は、「はい/いいえ」「成功/失敗」といった2値の結果を予測・分析する統計手法です。この手法は、ロジスティック回帰の発展形として位置づけられ、より柔軟で高度なモデリングを可能にします。例えば、「ある条件を満たすかどうか」「特定の事象が発生するかどうか」といった予測において、複数の要因の影響を詳細に分析できます。また、予測結果は0から1の間の確率として得られるため、結果の解釈が直感的で実務での活用がしやすい特徴があります。
この手法が特に注目される理由は、現実世界の複雑な関係性を表現できる点にあります。通常のロジスティック回帰では、説明変数と目的変数の間に単純な線形関係(多ければ多いほど良い、または少なければ少ないほど良い)を仮定します。しかし、実際のデータではより複雑な関係性が存在することがあります。例えば、「適度な量が最も効果的で、多すぎても少なすぎても効果が下がる」といった非線形な関係性や、「ある条件下では正の効果だが、別の条件下では負の効果になる」といった交互作用も、GLM - 二項分布では適切にモデル化することができます。
このアプローチを使用することで、より正確な予測モデルの構築と、より深い洞察の獲得が可能になります。また、過学習(オーバーフィッティング)のリスクが比較的低く、データサイズが小さめでも安定した結果が得られやすいという特徴があります。さらに、モデルの結果は統計的な裏付けを持っているため、意思決定の根拠として説得力があります。各要因が結果に与える影響の大きさや方向性を具体的な数値として示すことができ、「なぜそのような結果になったのか」という因果関係の理解にも役立ちます。ロジスティック回帰と比較すると、よりきめ細かな分析が可能で、現実の複雑な事象をより適切にモデル化できる点が大きな利点となっています。
1. どういった時に使えるのか
一般化線形モデル(二項分布)は、様々な分野で「Yes/No」の結果を予測・分析する際に活用できます。例えば、Eコマースでのキャンペーン効果を分析する場合、顧客の属性(セグメント、年齢層)、施策内容(タイプ、割引率)、コミュニケーション方法(メール、LINE、プッシュ通知)など、複数の要因が購買行動に与える影響を総合的に評価する必要があります。
また、金融分野では融資の返済遅延リスクの予測に活用され、取引履歴や収入といった基本情報に加え、過去の支払い行動パターンなど、複数の要因を組み合わせた分析が可能です。特に、収入と返済リスクの関係が単純な比例関係ではなく、一定の収入水準を超えると返済リスクが横ばいになるといった非線形な関係性も捉えることができます。
さらに工学分野では、機器の故障予測にも応用され、稼働時間や負荷状態、環境条件などから故障確率を予測します。例えば、温度と故障リスクの関係が、適温範囲では低く、高温や低温になるほど上昇するといったU字型の関係性もモデル化することができます。
参考となるデータ例:
- 顧客別の購入有無と属性データ
- 契約別の更新有無と取引データ
- 施策別の反応有無とメール配信情報データ
- 会員別の継続有無と行動データ
2. ユースケース
医療機関での使い方
- 疾病リスクの予測や早期発見のスクリーニングに使えます。
- 具体的には、患者の基本情報、生活習慣、検査値などから特定の疾病の発症確率を予測することで、リスク要因を特定できます。
- これにより、ハイリスク患者への予防的介入や検査優先度の決定に活用できます。
小売業での使い方
- 商品別のレコメンデーション効果予測に使えます。
- 具体的には、商品カテゴリー、価格帯、顧客の閲覧履歴などから、レコメンド商品への反応確率を予測することで、効果的な商品提案が可能になります。
- これにより、顧客別の最適な商品提案や、クロスセル施策の精度向上が実現できます。
品質管理担当者での使い方
- 検査工程の最適化に使えます。
- 具体的には、製品特性、製造条件、検査項目などから合格確率を予測することで、重点的に確認すべき項目を特定できます。
- これにより、効率的な検査計画の立案や品質改善施策の優先順位付けが可能になります。
リスク管理担当者での使い方
- 異常検知や事故予防に使えます。
- 具体的には、運転条件、環境要因、保守履歴などから故障や事故の発生確率を予測することで、リスク要因を事前に把握できます。
- これにより、予防保全の計画立案や安全対策の実施が可能になります。
3. Exploratoryで一般化線形モデル(二項分布)を実行する
使用するデータ
今回は「キャンペーン施策効果測定データ」を使用します。データはこちらからダウンロードが可能となっています。
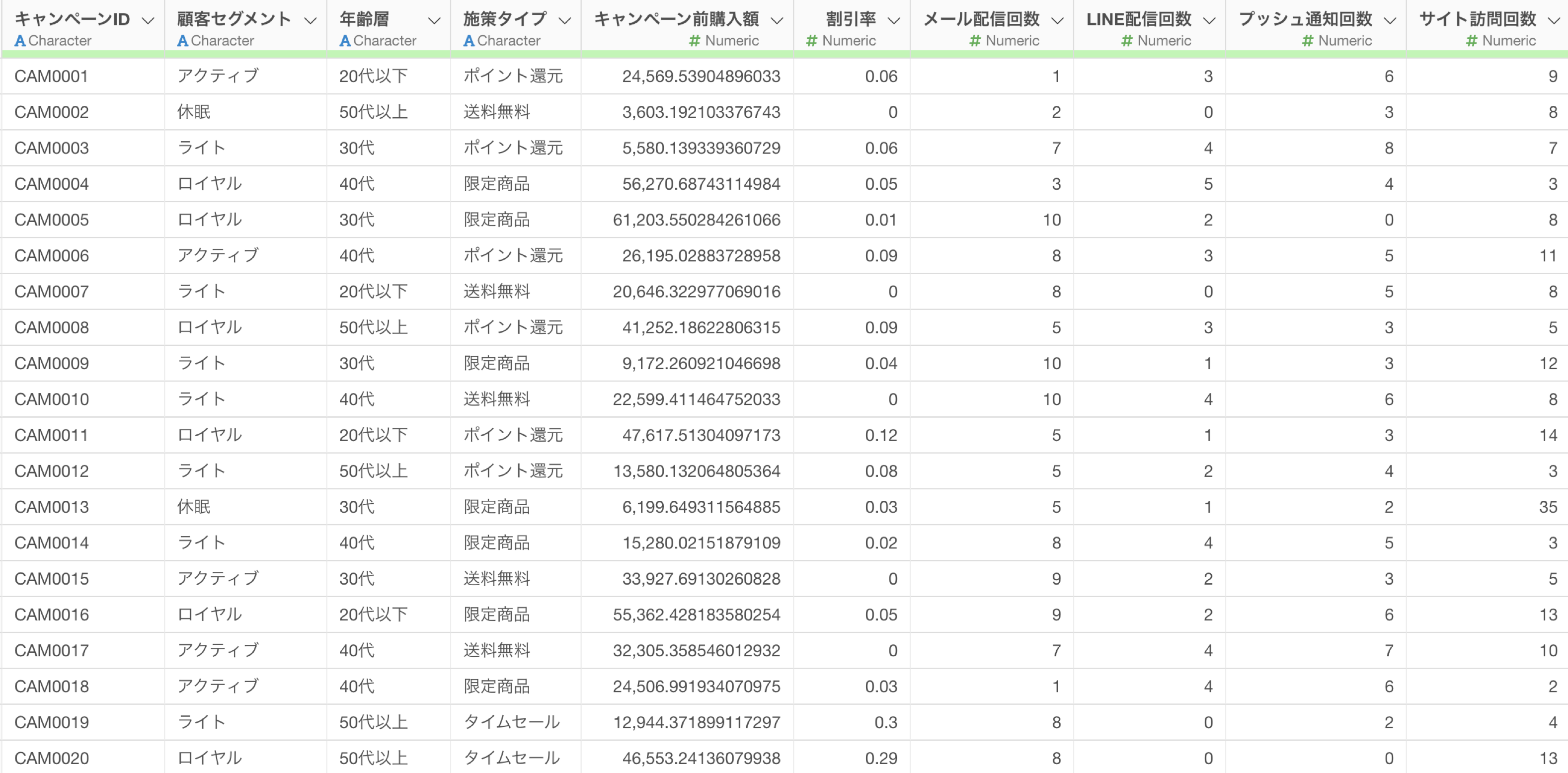
このデータは1行が1つのキャンペーン施策の結果を表しており、以下のような列が含まれています:
- 基本情報:キャンペーンID、顧客セグメント、年齢層
- 結果指標:キャンペーン反応(TRUE/FALSE)
- 施策情報:施策タイプ(ポイント還元、限定商品、送料無料、タイムセール)、割引率(%)
- コミュニケーション指標:メール配信回数、LINE配信回数、プッシュ通知回数
- 顧客行動指標:サイト訪問回数、メール開封率、LINE開封率、商品閲覧数、など。
一般化線形モデル(二項分布)を実行するためには、以下のようなデータ構造が必要となります:
- 目的変数(キャンペーン反応)は TRUE/FALSE の2値である必要があります
- 予測変数は数値型(配信回数、開封率など)やカテゴリ型(顧客セグメント、施策タイプなど)などの変数を使用します。
- キャンペーンIDのような識別子は分析から除外する必要があります。
アナリティクスを作成する
キャンペーン施策効果測定データから「アナリティクス・ビュー」を開きます。
タイプに「一般化線形モデル」を選び、「GLM - 二項分布」を選択します。
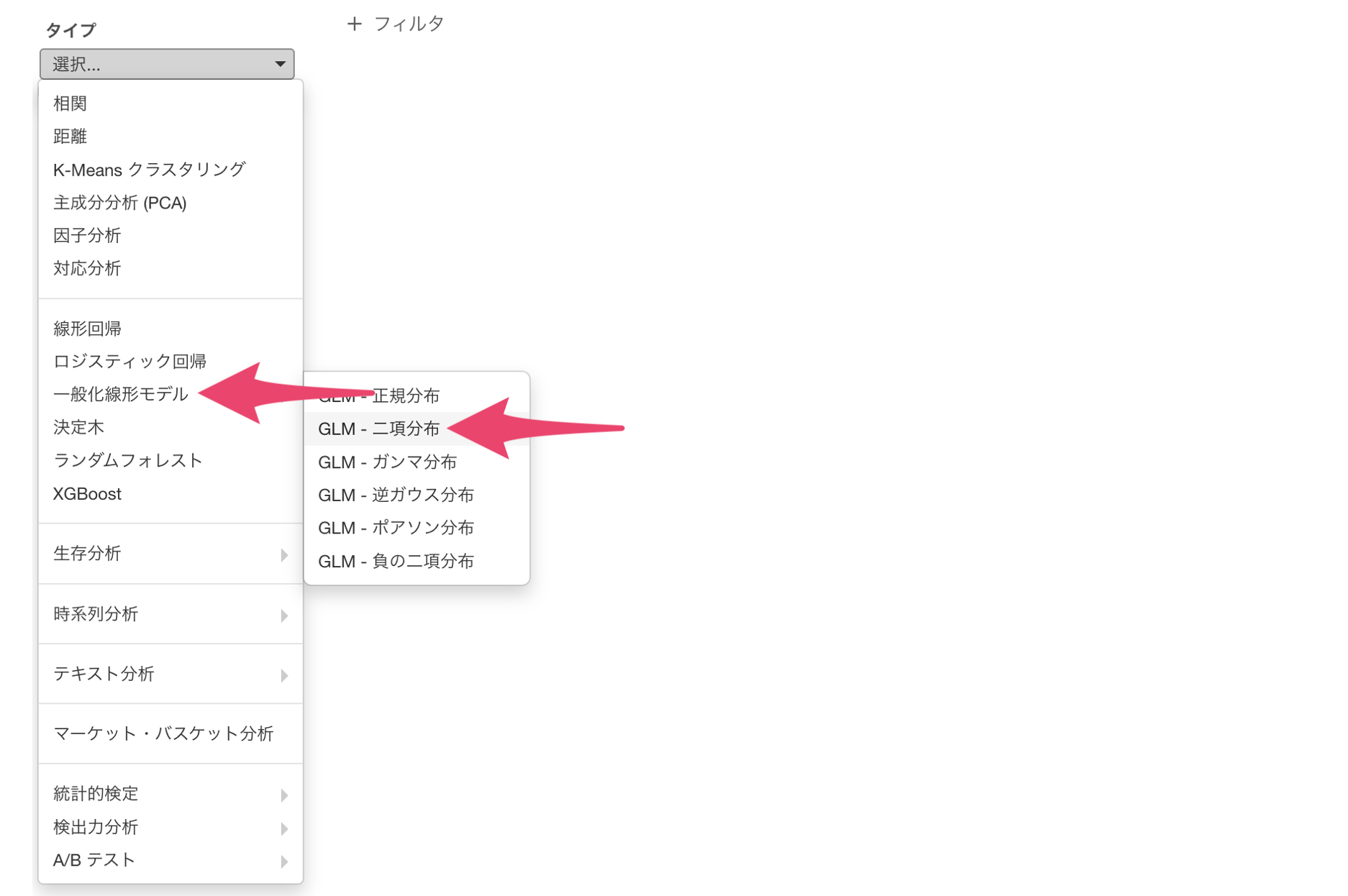
目的変数には、「キャンペーン反応」の列を割り当てます。
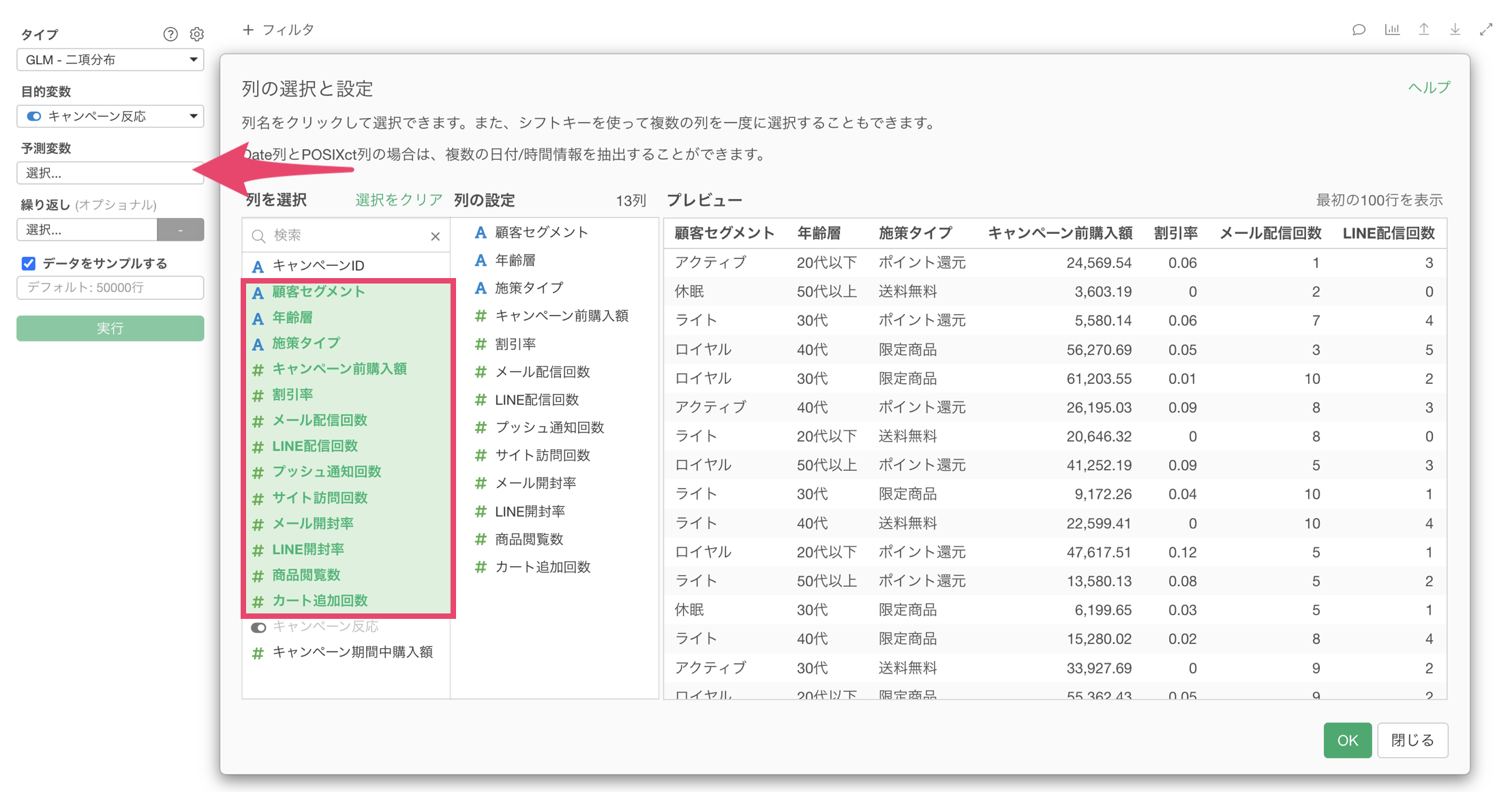
予測変数には、「顧客セグメント」から「カート追加回数」までの列を選択します。
最後に、「実行」ボタンをクリックして実行結果を確認します。
結果の解釈
一般化線形モデル(二項分布)では、キャンペーン施策の効果を多角的に分析するために以下のタブが用意されています。
多重共線性
「多重共線性」タブをクリックすると、予測変数間の相関が強すぎる(VIF > 10)組み合わせがないかを確認できます。VIFが10以上の変数がある場合、モデルの信頼性に影響を与える(傾きが不安定になる)可能性があるため、変数の選択を見直す必要があります。
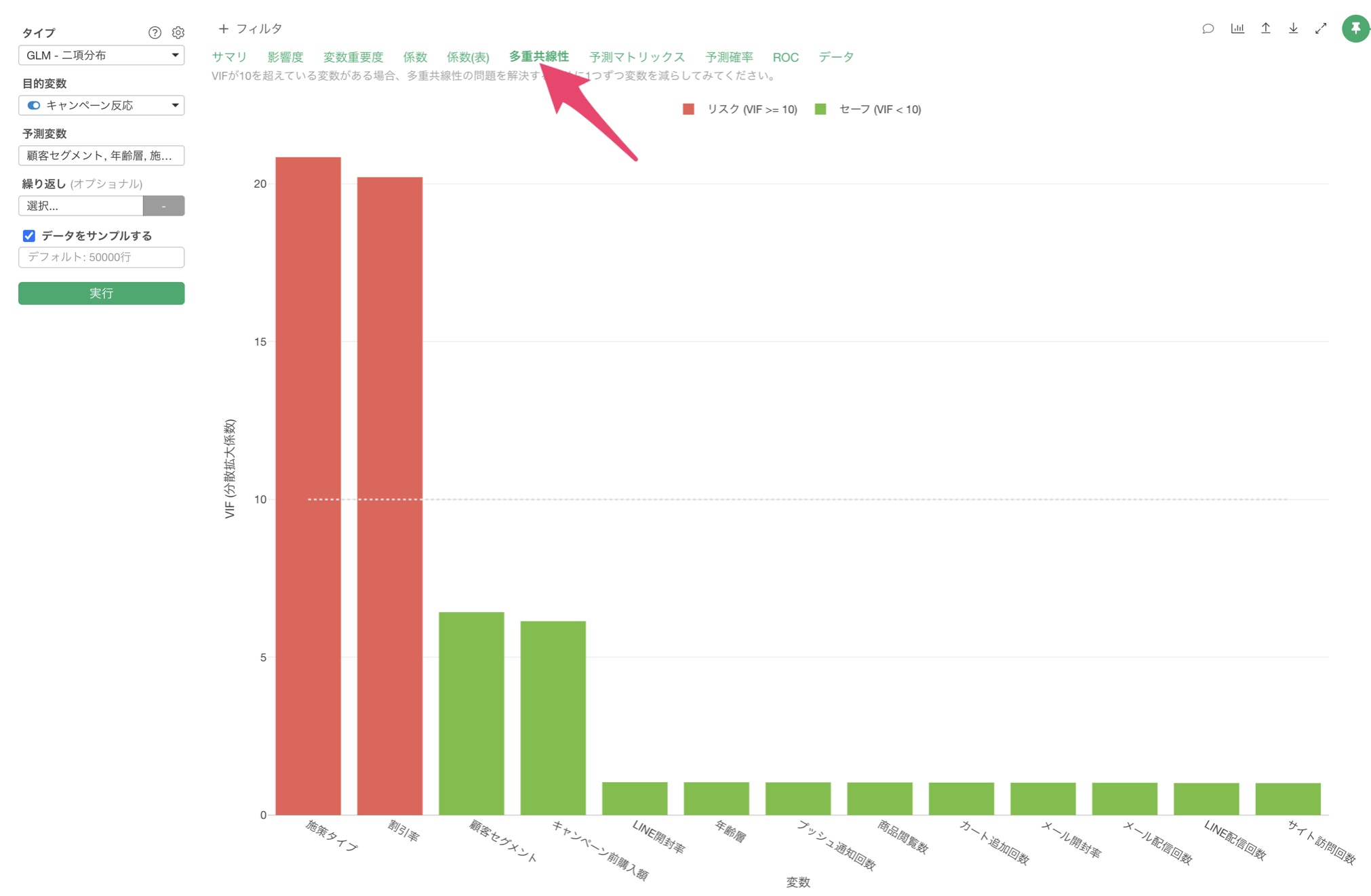
今回は「施策タイプ」と「割引率」の2つの列がVIFが10以上であり、予測変数間の相関が強いという結果になっています。
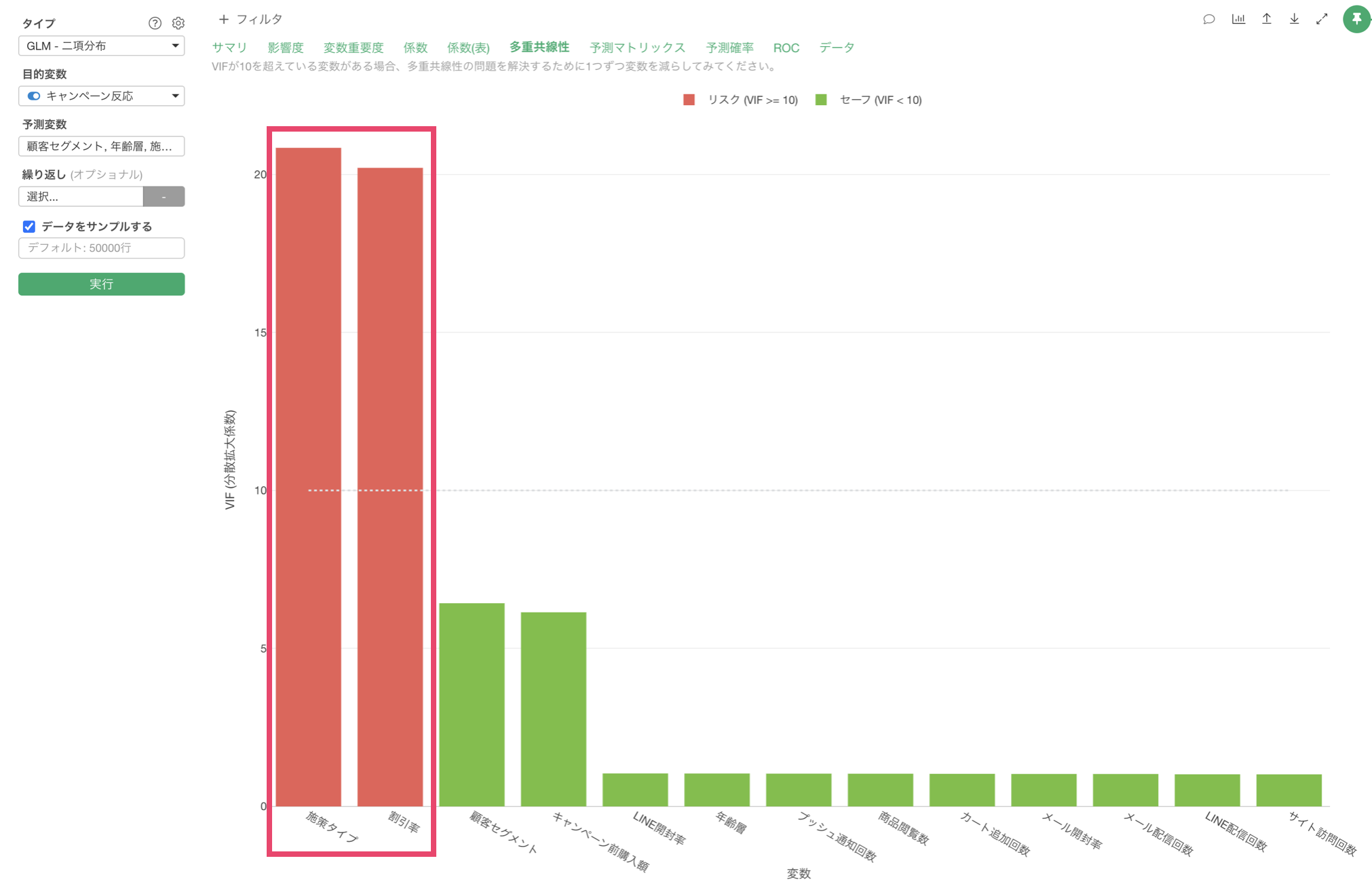
理由としては、施策タイプによって割引率には大きく違いがあり、これらの変数は相関が強いために多重共線性が発生しているという結果になっていました。
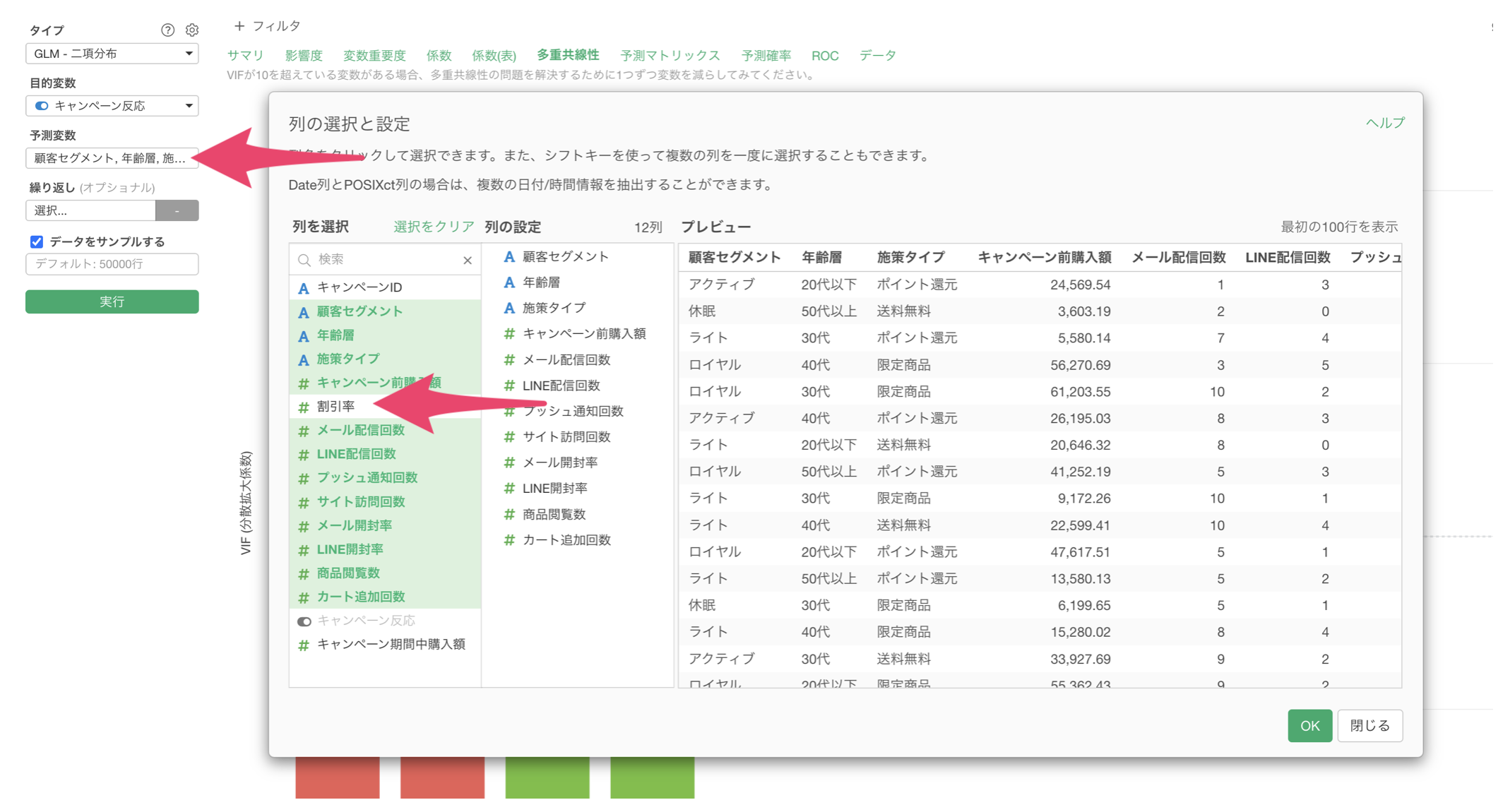
そのため、予測変数から「割引率」を除いて、実行をします。
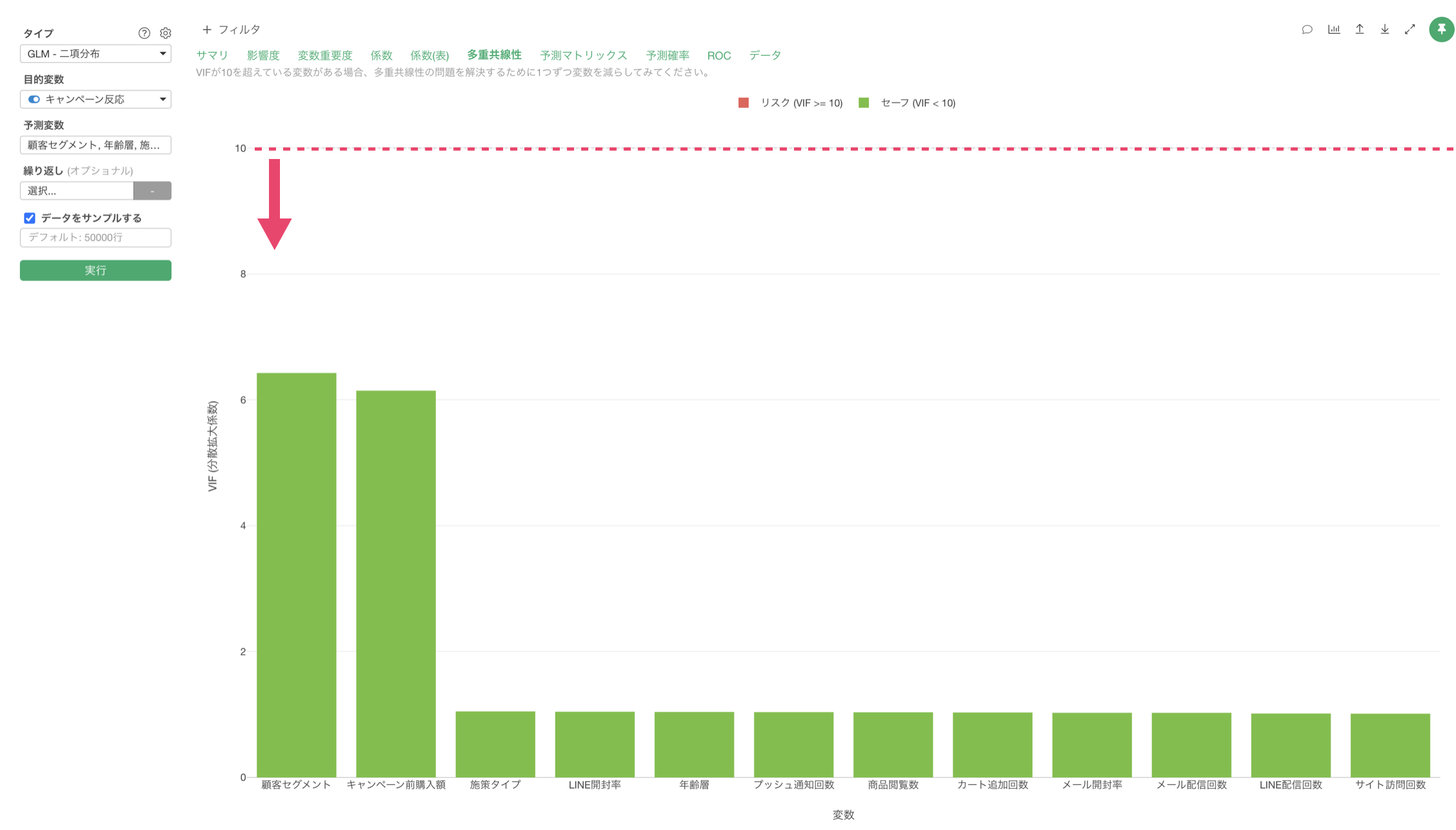
これによって、VIFが10以上のものはないため、予測変数同士に相関が強すぎる変数の組み合わせが無くなり、モデルが不安定であることはないことがわかります。
変数重要度
「変数重要度」タブをクリックすると、目的変数を予測する上でどの変数が重要なのかを確認することができます。
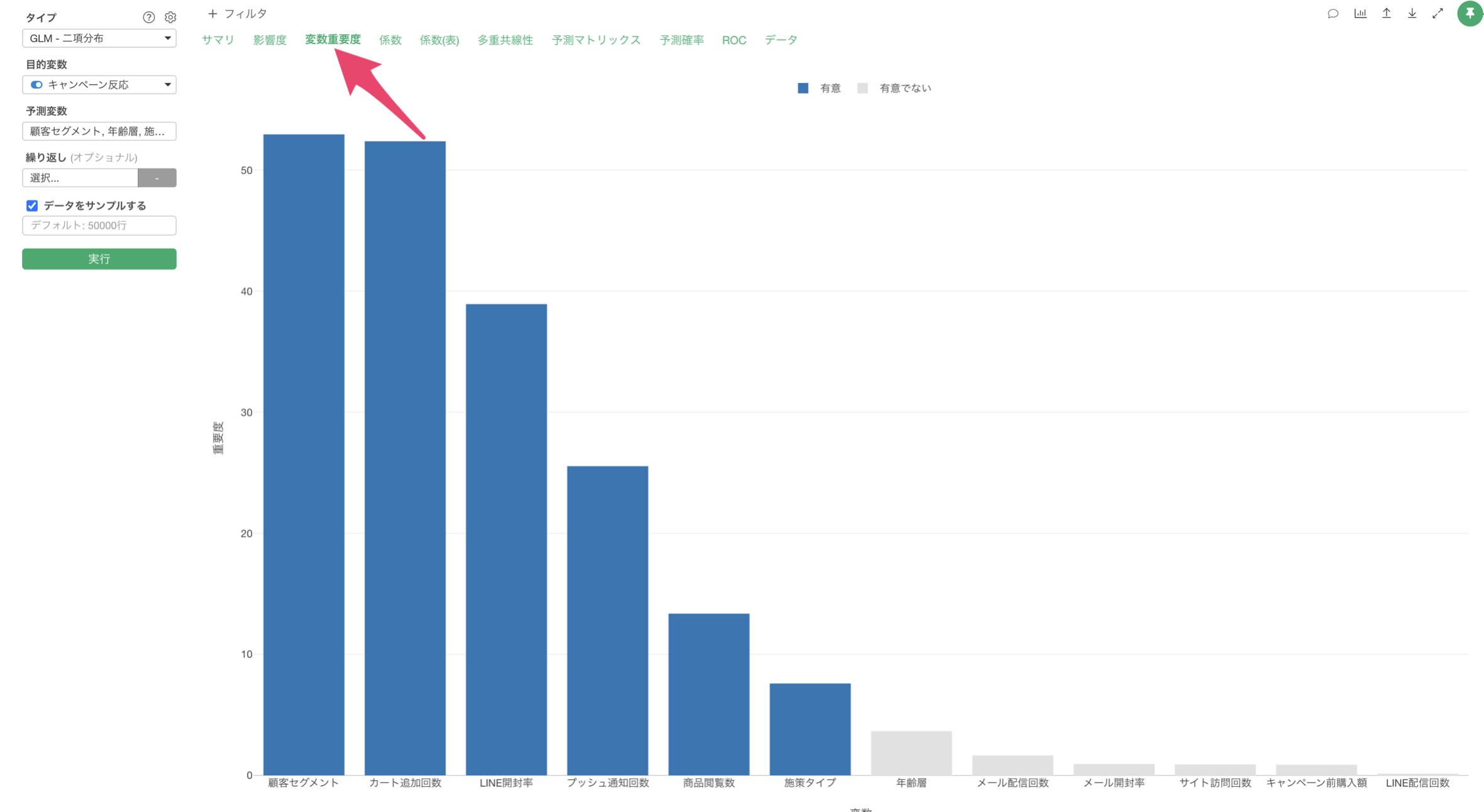
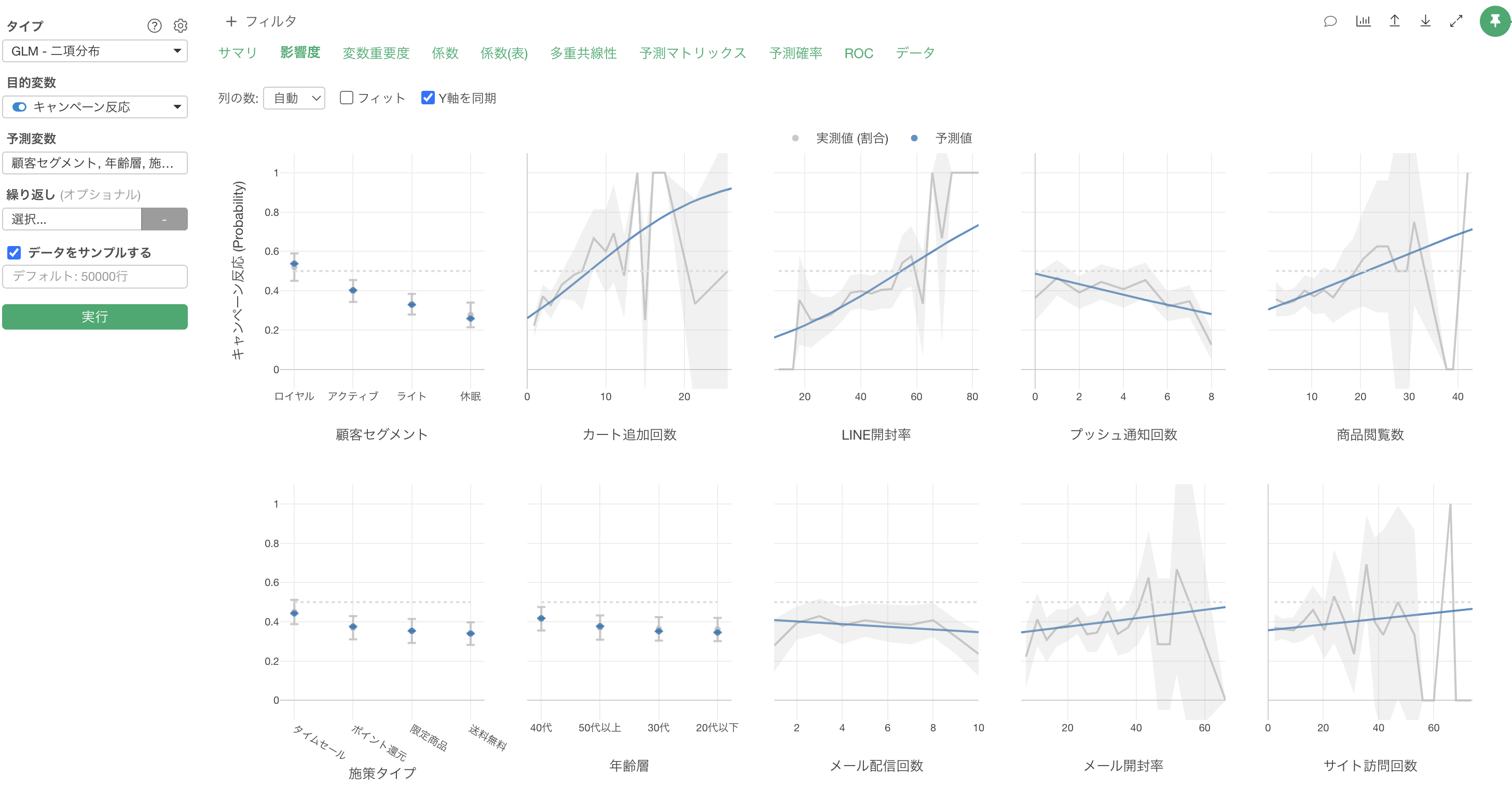
この結果から、キャンペーンに反応するかどうかの予測に最も重要な変数は顧客セグメントであり、次いでカート追加回数、LINE開封率の順となっていることがわかります。
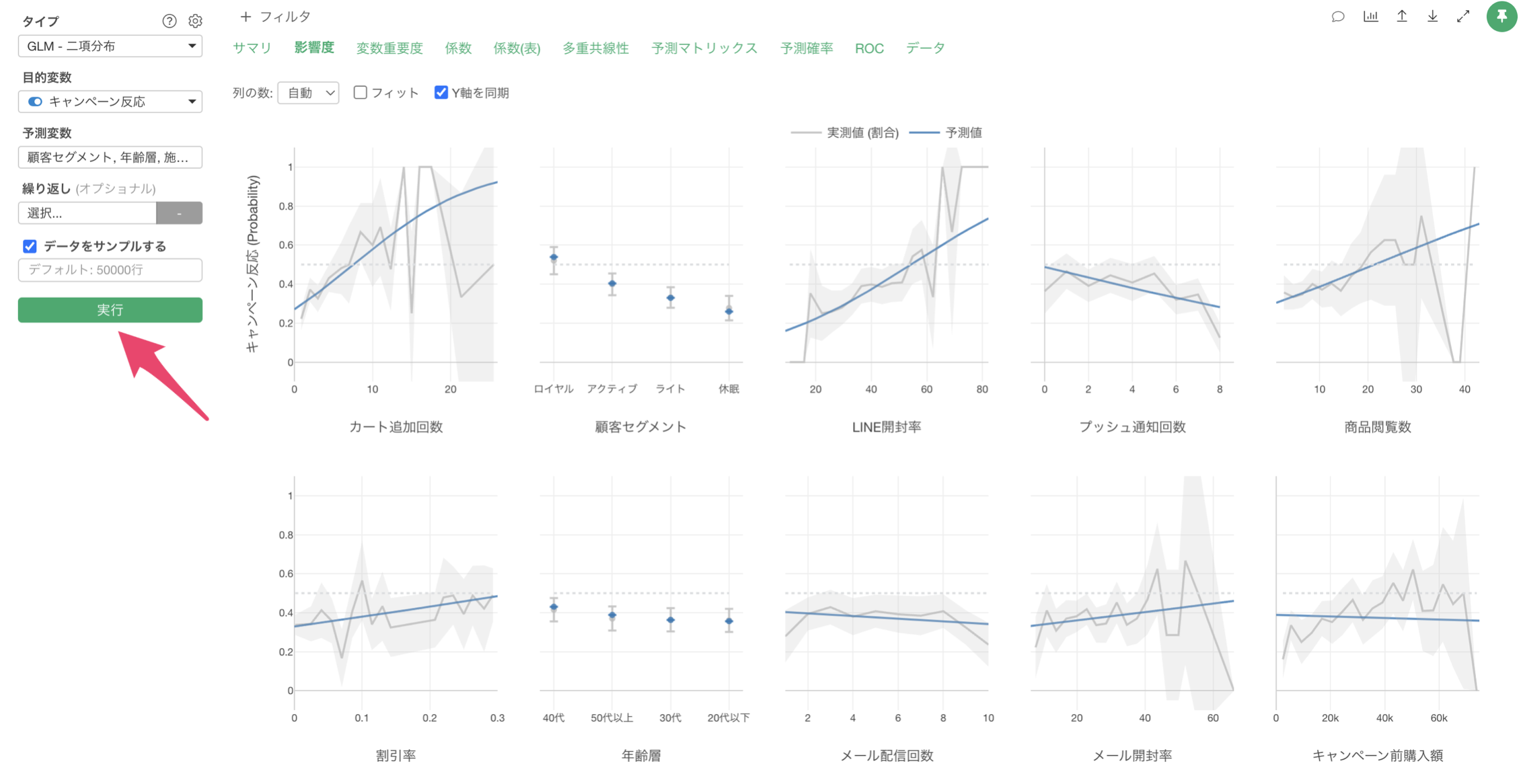
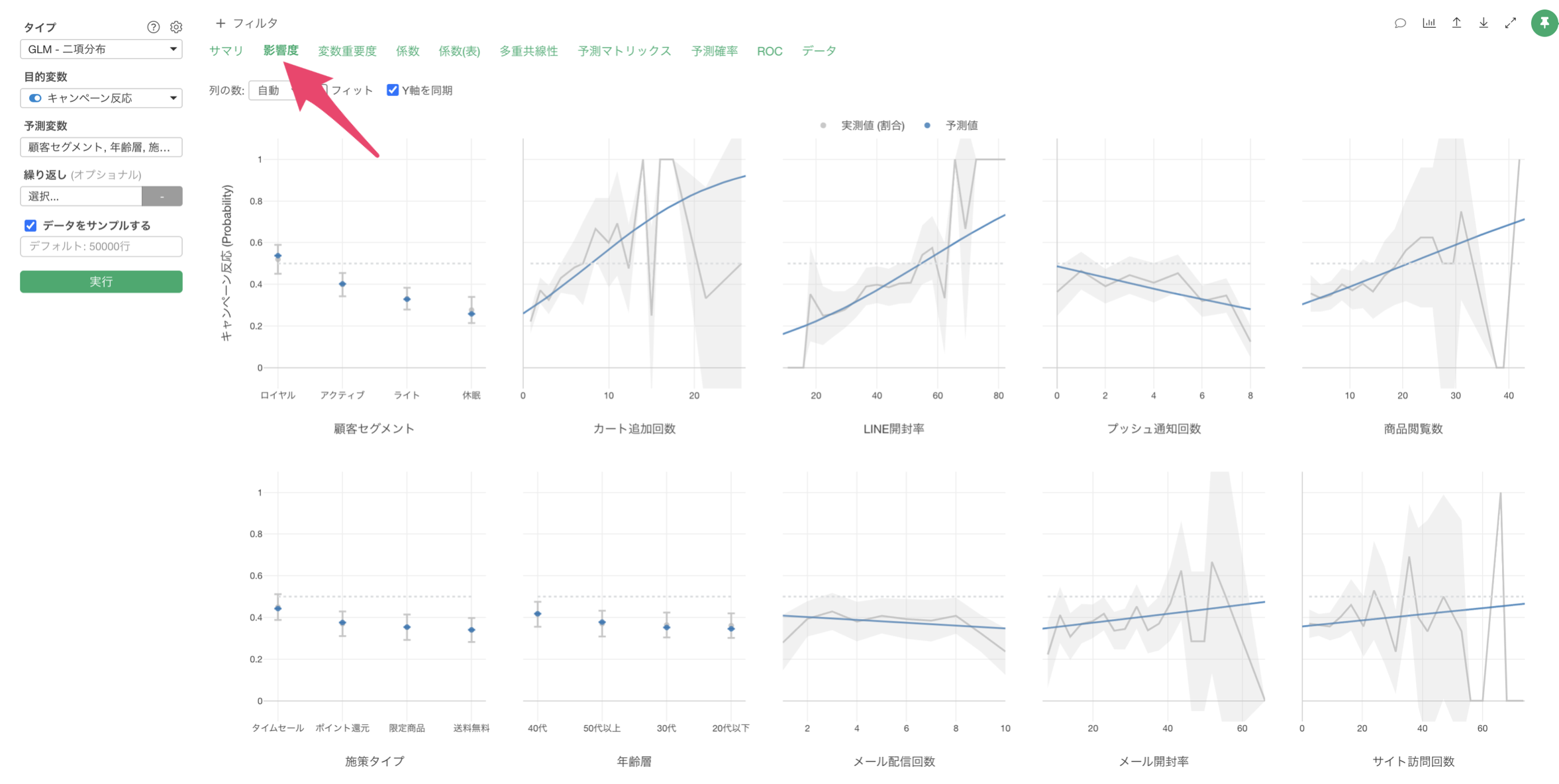
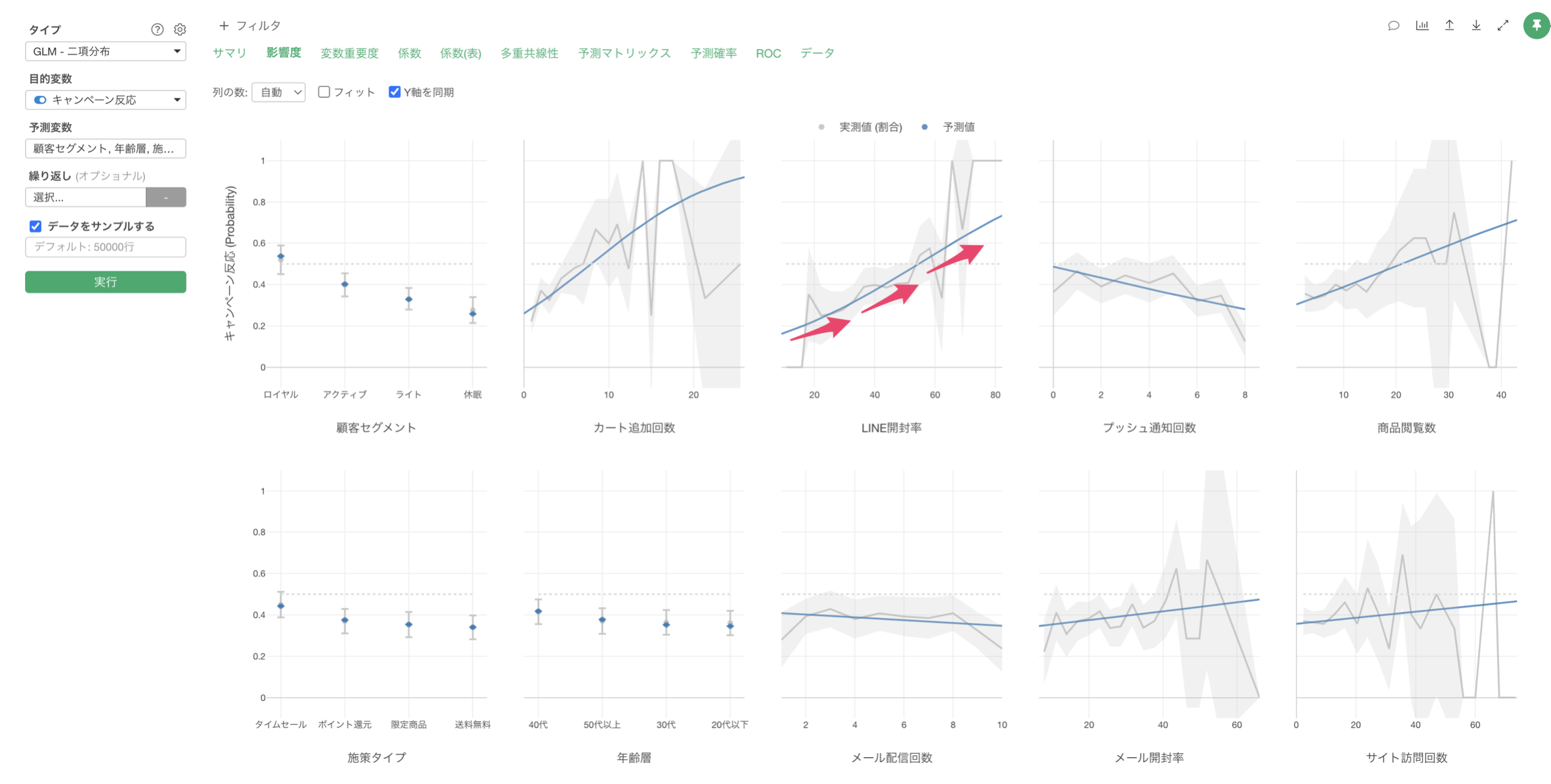
影響度
「影響度」タブでは、各予測変数がキャンペーン反応に与える影響の方向と強さを確認することができます。
例えば、顧客セグメントがロイヤル顧客の場合は、他のセグメントに比べてキャンペーンの反応率が高いことがわかります。一方で顧客セグメントが休眠の場合は、キャンペーンの反応率が低いようです。
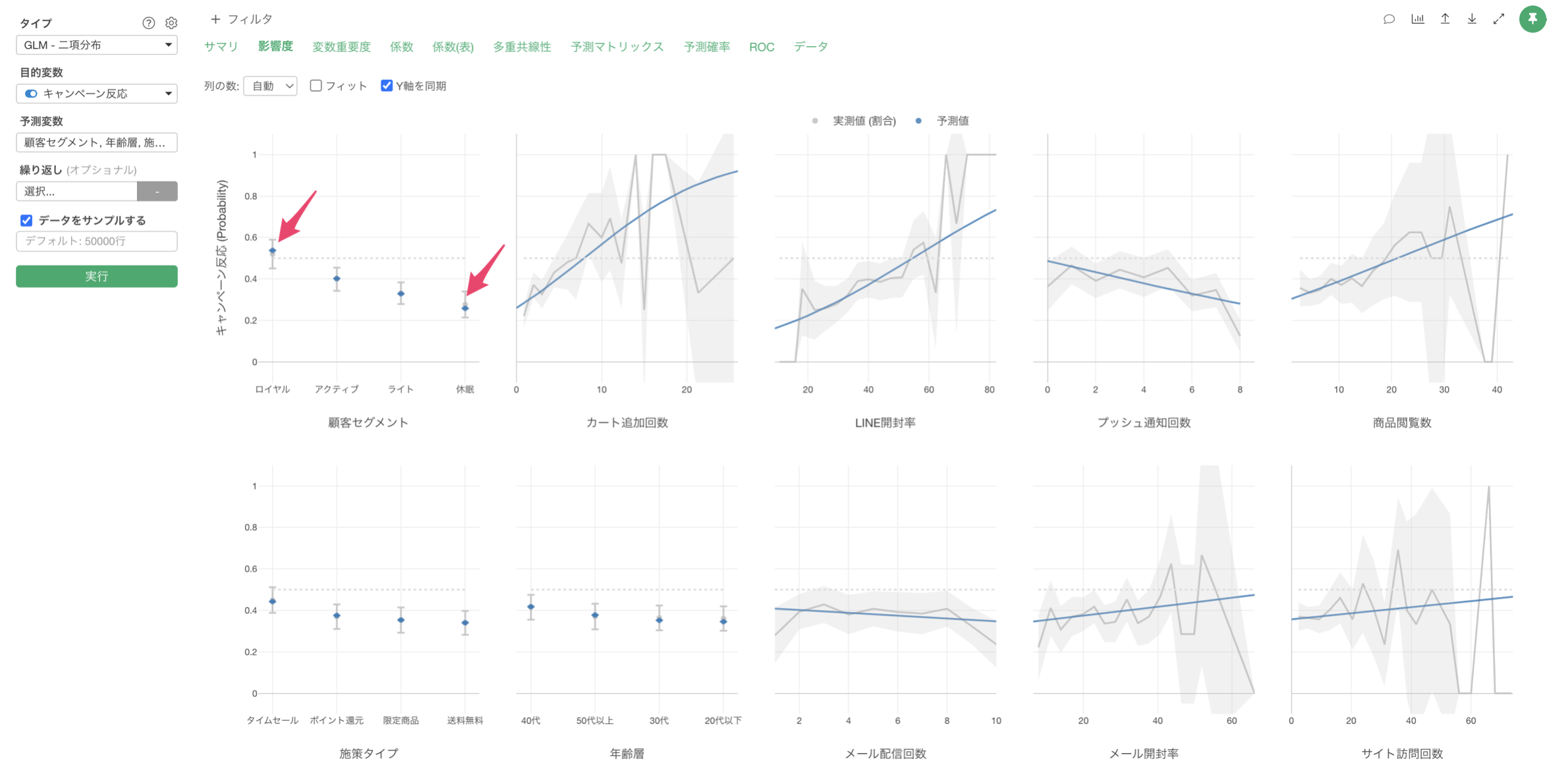
例えば、LINEの開封率の値が上がると、キャンペーンの反応率も増えることが確認出来ます。
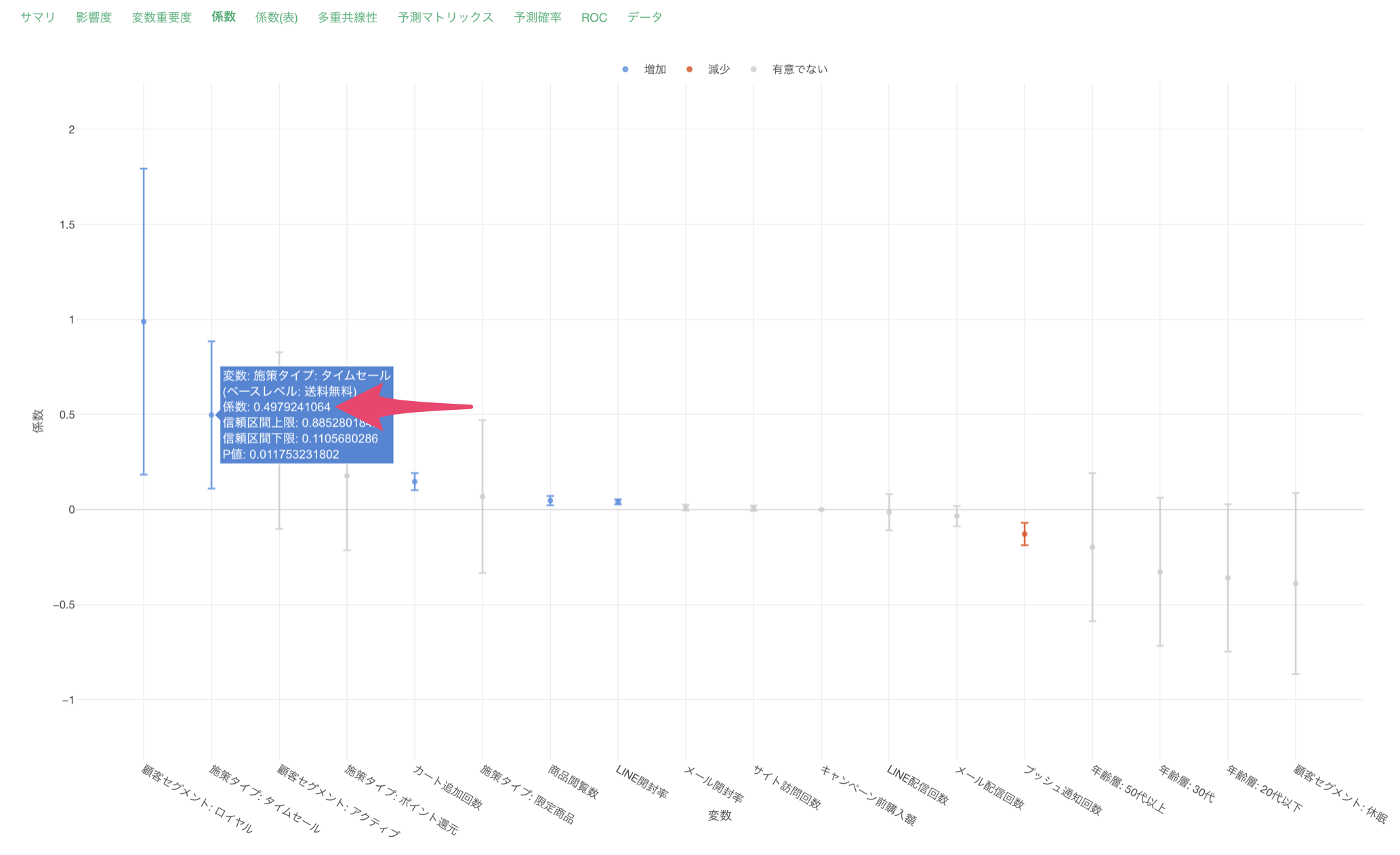
係数
「係数」タブでは、各予測変数の係数とその統計的有意性を確認することができます。
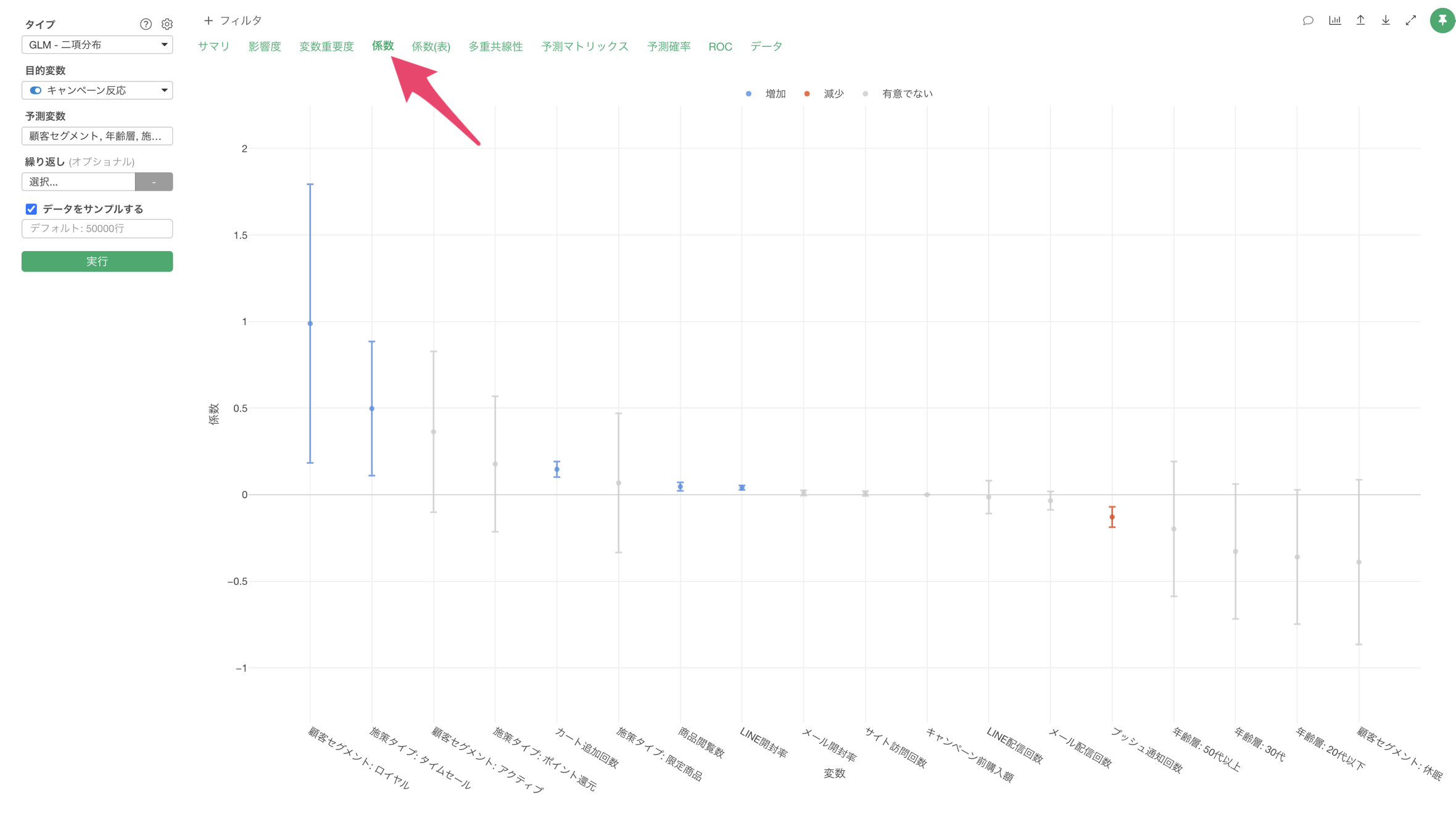
この結果から、各変数の効果の大きさと方向性を具体的な数値で確認できます。係数が正の値は、その変数が増加するとキャンペーンの反応率も増加することを示し、負の値は減少することを示します。P値が0.05未満の変数は、統計的に有意な影響を持っていると判断できます。
また、GLM - 二項分布の係数は、オッズ比の対数(log-odds)として表現されています。
LINE開封率の係数は0.0408ですが、オッズ比で解釈するために指数化すると、1%増加すると、キャンペーンに反応する確率のオッズ(可能性)が約1.042倍(4.2%増加)すると言った解釈になります。
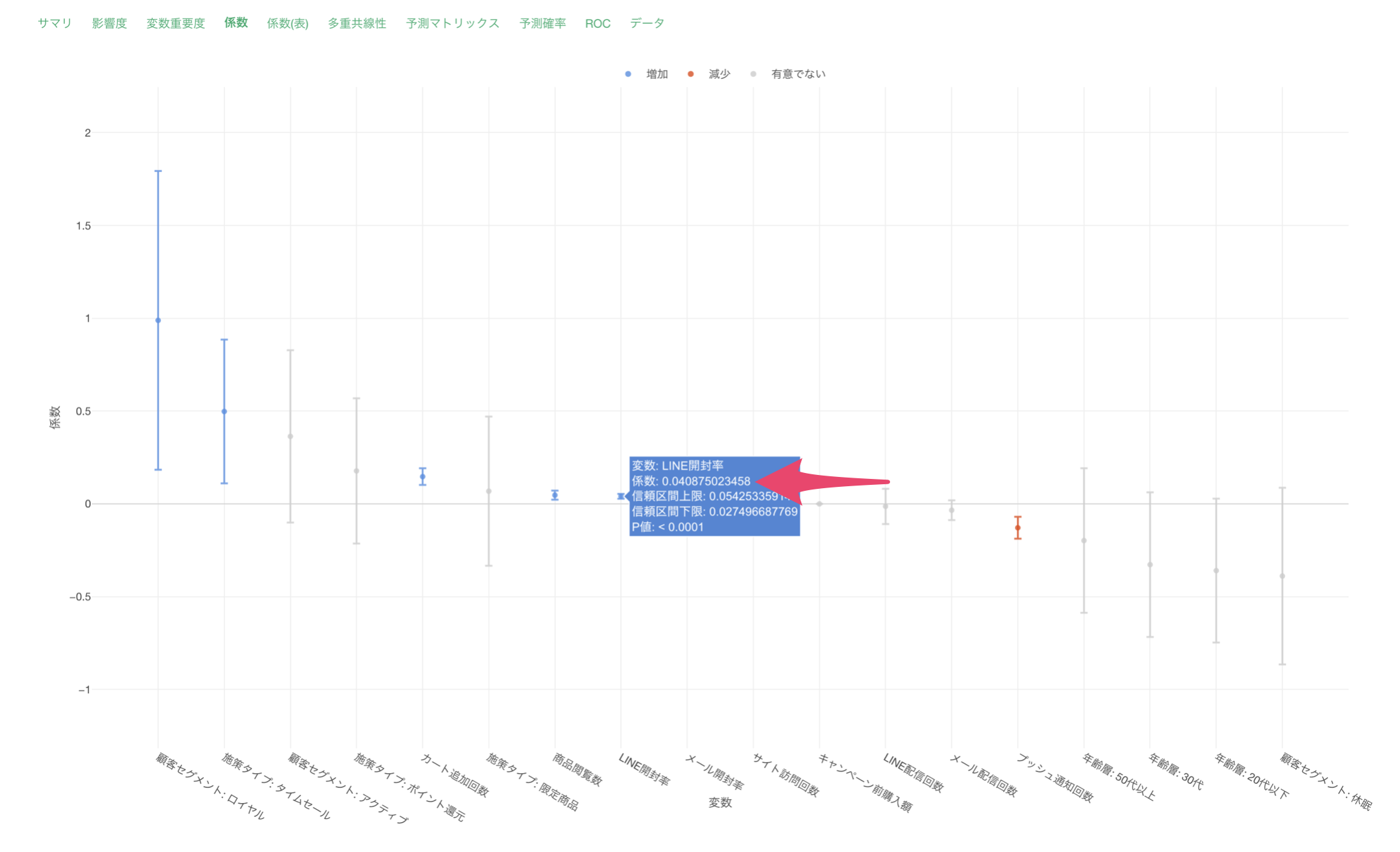
施策タイプが送料無料からタイムセールになることで、キャンペーンに反応する確率のオッズ(可能性)が約1.645倍(64.5%増加)になるといった解釈となります。
サマリ
「サマリ」タブをクリックすると、モデル全体の予測精度を確認することができます。
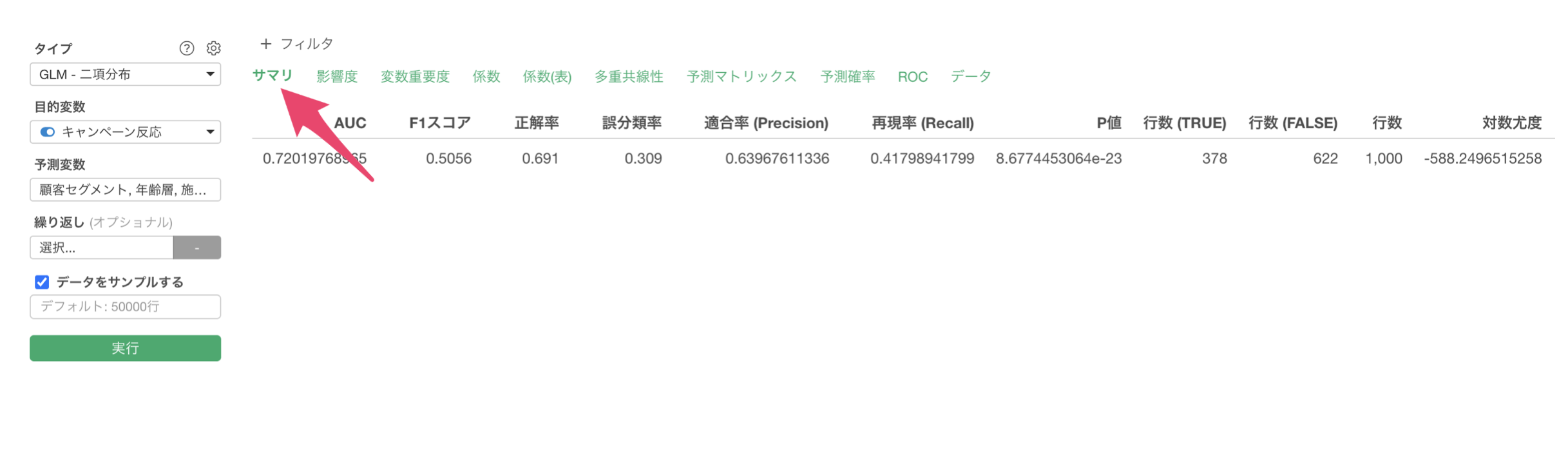
AUCはこのモデルに使われている予測変数が目的変数のTRUEとFALSEのデータをどれだけうまく切り分けることができるかを示します。
今回のモデルでのAUCは0.72であり、この予測モデルは一定の予測能力はあるものの、改善の余地があることを示しています。

4. まとめ
GLM - 二項分布は、キャンペーン反応や購入有無といった「Yes/No」の2値データを分析する際に、特に複雑な要因関係がある場合に効果的な分析手法です。
今回のキャンペーン施策の効果分析では、反応有無に影響を与える主な要因として、顧客セグメント、コミュニケーション施策(LINE開封率など)、施策タイプ(タイムセールなど)が関係があることがわかりました。具体的には、LINE開封率が1%上昇すると反応確率が約4.2%増加し、タイムセールは送料無料と比べて約1.65倍の反応が期待できることがわかりました。
これらの分析結果から、キャンペーンの反応率を向上させるためには、顧客セグメントに応じた施策設計、LINEの開封率を高める工夫、効果的な施策タイプの選択などが重要だと考えられます。