一般化線形モデル - GLM - ガンマ分布の使い方
一般化線形モデル(GLM)のガンマ分布は、0以上の小数を含む数値データを分析する際に特に有用な統計モデルです。通常の線形回帰では適切に扱えない、値が0以上で右に裾が長い分布を持つデータに対して効果的です。特に、保険金支払額、医療費、修理費用など、金額に関連するデータ分析でよく使用されます。
ガンマ分布GLMの特徴は、データの分散が平均の二乗に比例するという性質を持っていることです。これは、多くの金銭的なデータでみられる特徴と一致しています。例えば、保険金支払いデータでは、平均支払額が大きくなるほど、支払額のばらつきも大きくなる傾向がありますが、このような現象をガンマ分布GLMは適切にモデル化することができます。
さらに、ガンマ分布GLMは、説明変数が目的変数に対して乗法的な効果を持つことを仮定しています。これは、例えば年齢が1歳増えることで支払額が一定の割合で増加するといった、実務でよく観察される関係性を自然にモデル化できることを意味します。また、対数リンク関数を使用することで、予測値が常に正の値となることが保証され、金額データの分析に適しています。
1. どういった時に使えるのか
ガンマ分布GLMは、特に金額や時間など、0以上の値を取り、平均が大きくなるほどばらつきも大きくなるような現象を分析する際に適しています。例えば、保険業界での保険金支払額の予測では、事故の重大性や契約者の属性によって支払額が変動しますが、その変動は平均支払額が大きいほど大きくなる傾向があります。また、医療分野での入院期間の分析では、疾患の重症度や患者の年齢によって入院期間が変動し、平均期間が長くなるほどばらつきも大きくなる傾向があります。
このモデルは、説明変数が目的変数に対して掛け算的な効果を持つ場合に特に有効です。たとえば、自動車保険の修理費用分析では、車両の年式が1年古くなることで修理費用が一定の割合で増加するような関係性を適切にモデル化できます。また、製造業での製品不良率分析において、製造時間と不良率の関係性を分析する際にも、時間の経過とともに不良率が一定の割合で変化するような現象をモデル化できます。
以下のようなデータ例で特に有効です:
- 保険金支払データ(契約者属性、保険種類、事故状況と支払額の関係)
- 医療費データ(患者属性、疾患、治療内容と医療費の関係)
- 修理費用データ(製品年齢、故障内容、部品コストと修理費用の関係)
- 販売時間データ(商品特性、販売チャネル、季節性と販売所要時間の関係)
2. ユースケース
保険業界での使い方
- 保険金支払部門では、新規契約の査定や保険料設定の際に使えます。
- 具体的には、契約者の年齢、既往歴、生活習慣などの要因が支払額にどの程度影響を与えるかを分析する際にガンマ分布GLMを使うことで、各要因の影響度を正確に把握できるようになります。
- これにより、リスク要因に応じた適切な保険料設定や、支払リスクの高い契約の早期発見といった施策を実施できます。
医療業界での使い方
- 病院の経営企画部門では、診療科別の医療費予測に使えます。
- 具体的には、患者の年齢、疾患の種類、治療方法などが医療費にどのように影響するかを分析する際にガンマ分布GLMを使うことで、医療費の変動要因を特定できるようになります。
- これにより、診療科別の予算配分の最適化や、高額医療費が発生しやすい患者群の特定といった施策を実施できます。
データアナリストでの使い方
- ビジネスコンサルティングの場面で、クライアントの費用分析に使えます。
- 具体的には、プロジェクトの規模、期間、投入リソースなどがコストにどのように影響するかを分析する際にガンマ分布GLMを使うことで、コスト変動の要因を特定できるようになります。
- これにより、プロジェクトの予算策定や、コスト削減施策の提案といった具体的なアクションにつなげることができます。
品質管理エンジニアでの使い方
- 製造業の品質管理部門で、製品の不良率分析に使えます。
- 具体的には、製造条件、材料特性、環境要因などが不良率にどのように影響するかを分析する際にガンマ分布GLMを使うことで、不良発生のメカニズムを理解できるようになります。
- これにより、製造条件の最適化や、重点的な品質管理ポイントの特定といった施策を実施できます。
3. Exploratoryで一般化線形モデル(GLM - ガンマ分布)を実行する
使用するデータ
今回は「保険契約データ」を使用します。データはこちらからダウンロードが可能となっています。
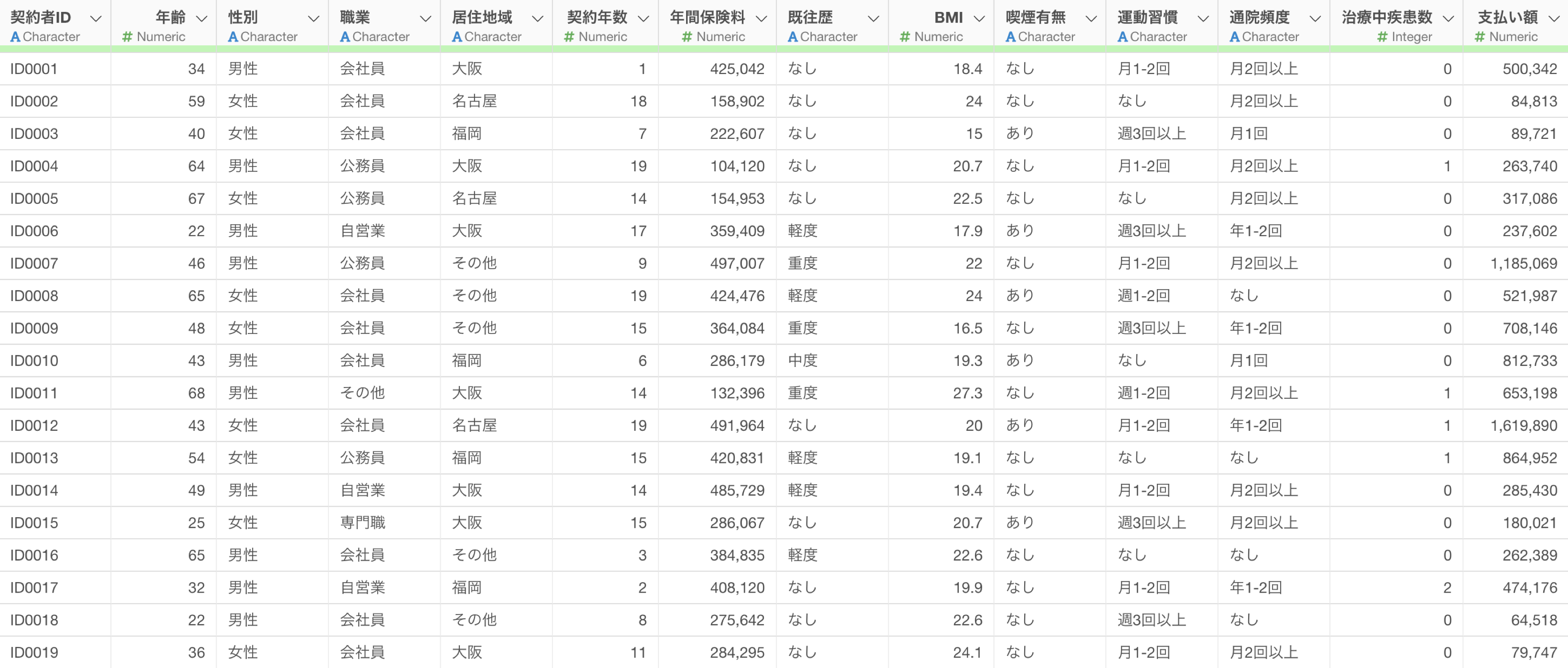
このデータは保険契約者の情報を含むデータセットで、1行が1契約者を表し、列には年齢や性別といった契約者の属性情報や、保険金の支払い額のデータなどがあります。
ガンマ分布GLMを作るためには、以下のようなデータの構造が必要となります。
- 目的変数は0より大きい連続値であること
- 目的変数の分散が平均の二乗に比例する傾向があること
- 予測変数は数値型(例:年齢、契約年数)やカテゴリ型(例: 性別、運動習慣)などの変数を使用します。
アナリティクスを作成する
保険契約データから「アナリティクス・ビュー」を開きます。
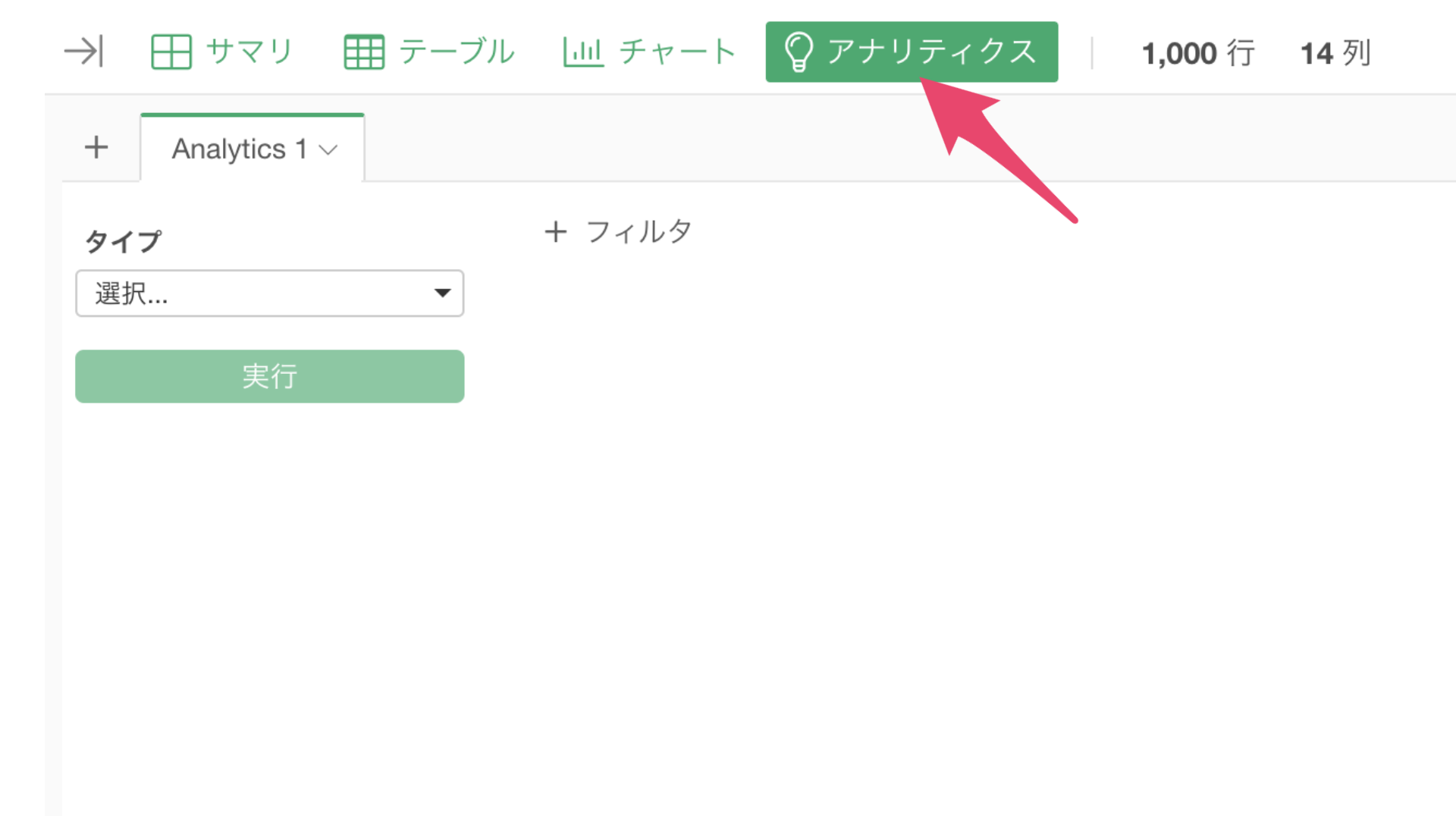
タイプに「一般化線形モデル」を選び、「GLM - ガンマ分布」を選択します。
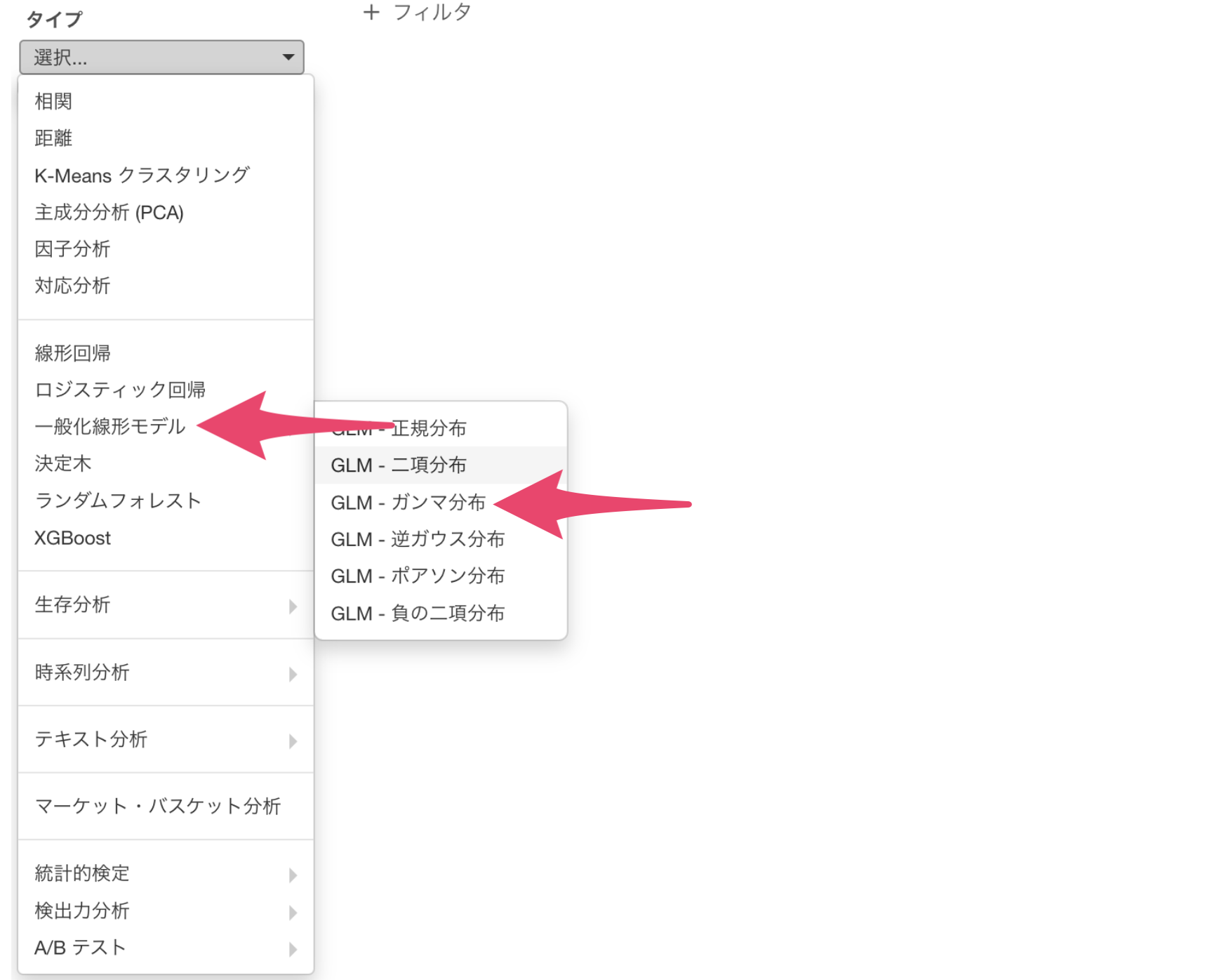
目的変数には、「支払い額」の列を割り当てます。
予測変数には、「年齢」から「治療中疾患数」までの列を選択して割り当てます。
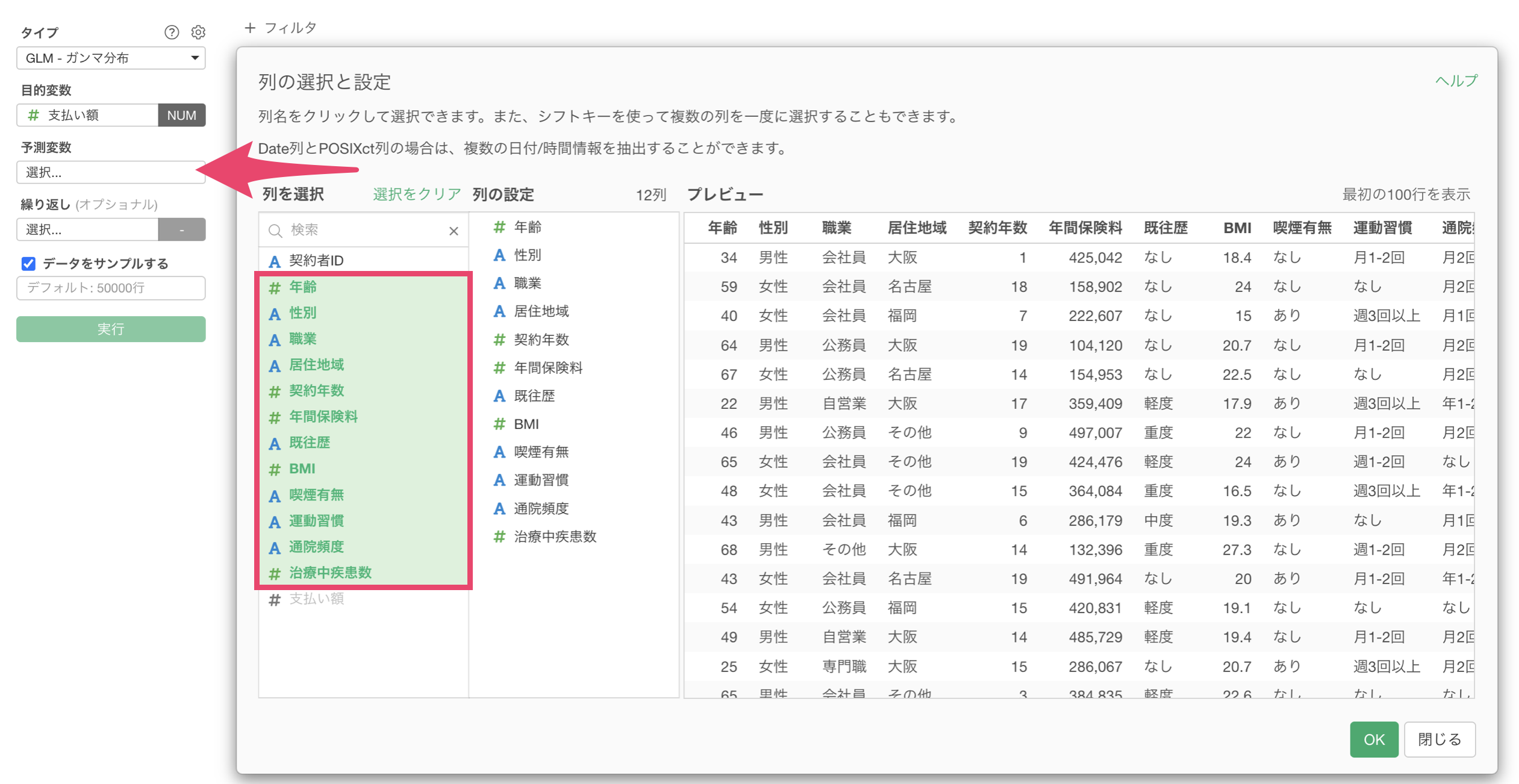
最後に、「実行」ボタンをクリックして実行結果を確認します。
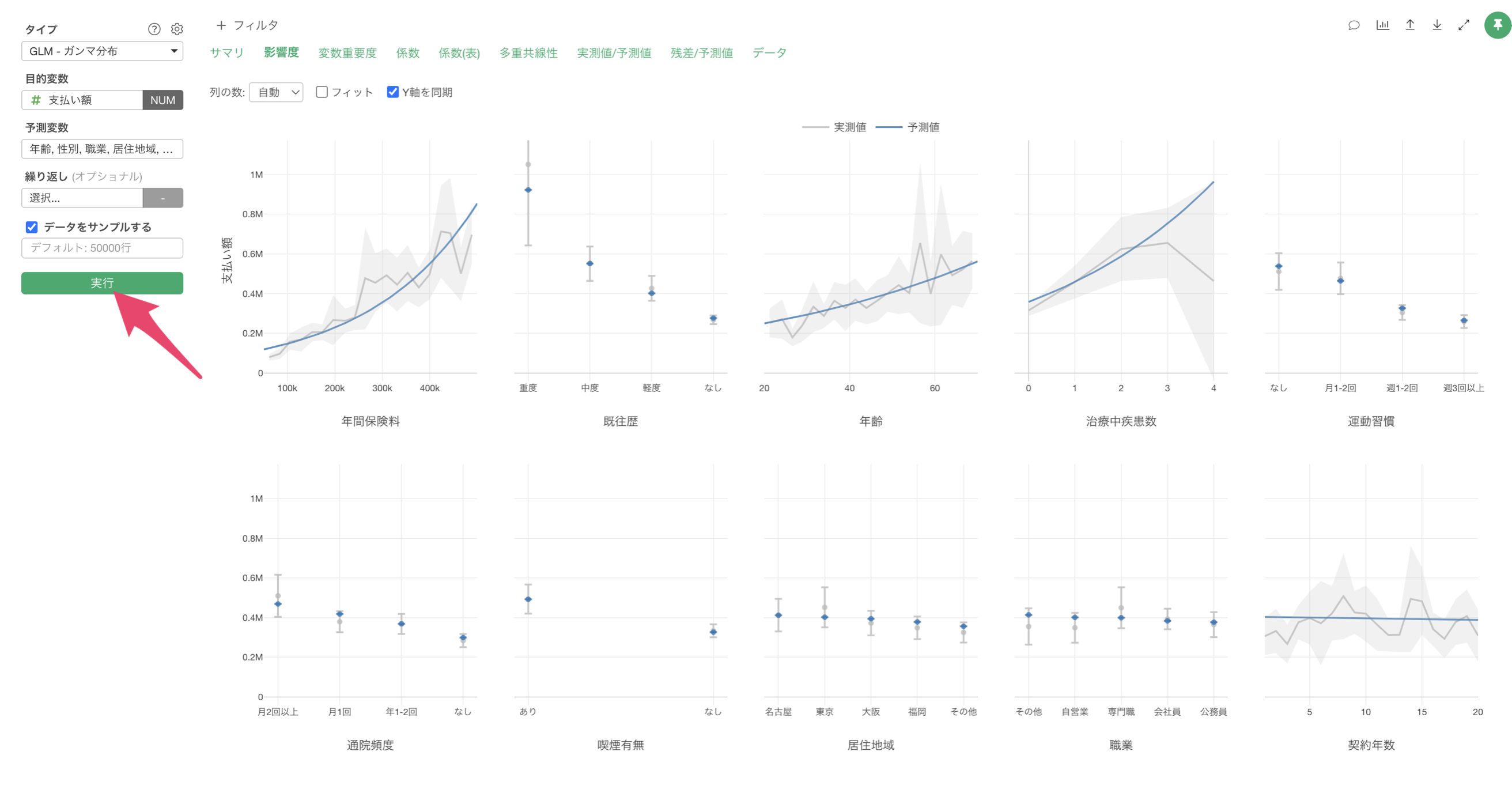
結果の解釈
一般化線形モデル(GLM - ガンマ分布)では、保険金支払額に影響を与える要因を解釈するために以下のタブが用意されています。
多重共線性
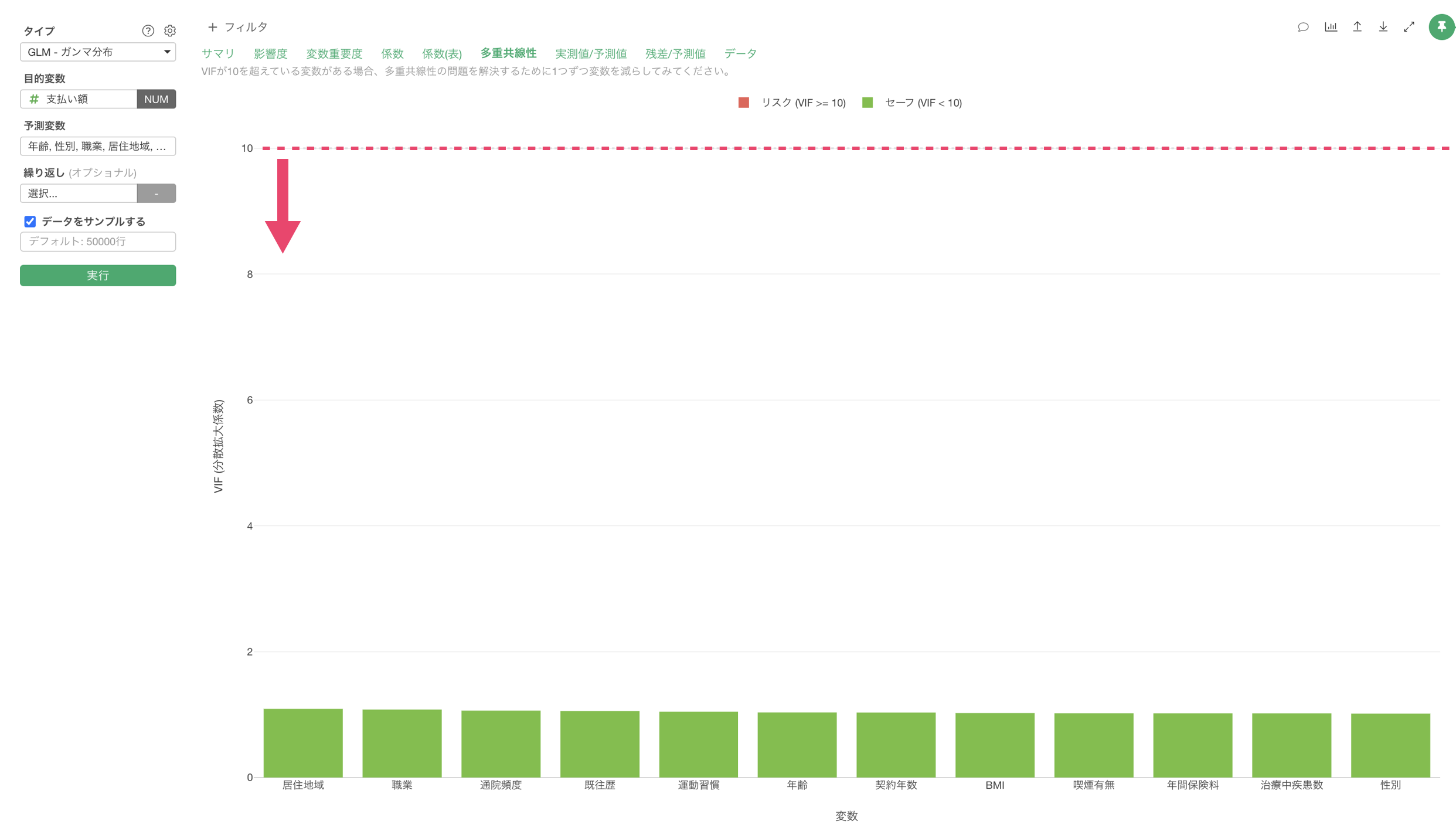
「多重共線性」タブをクリックすると、予測変数間の相関が強すぎる(VIF > 10)組み合わせがないかを確認できます。VIFが10以上の変数がある場合、モデルの信頼性に影響を与える(傾きが不安定になる)可能性があるため、変数の選択を見直す必要があります。
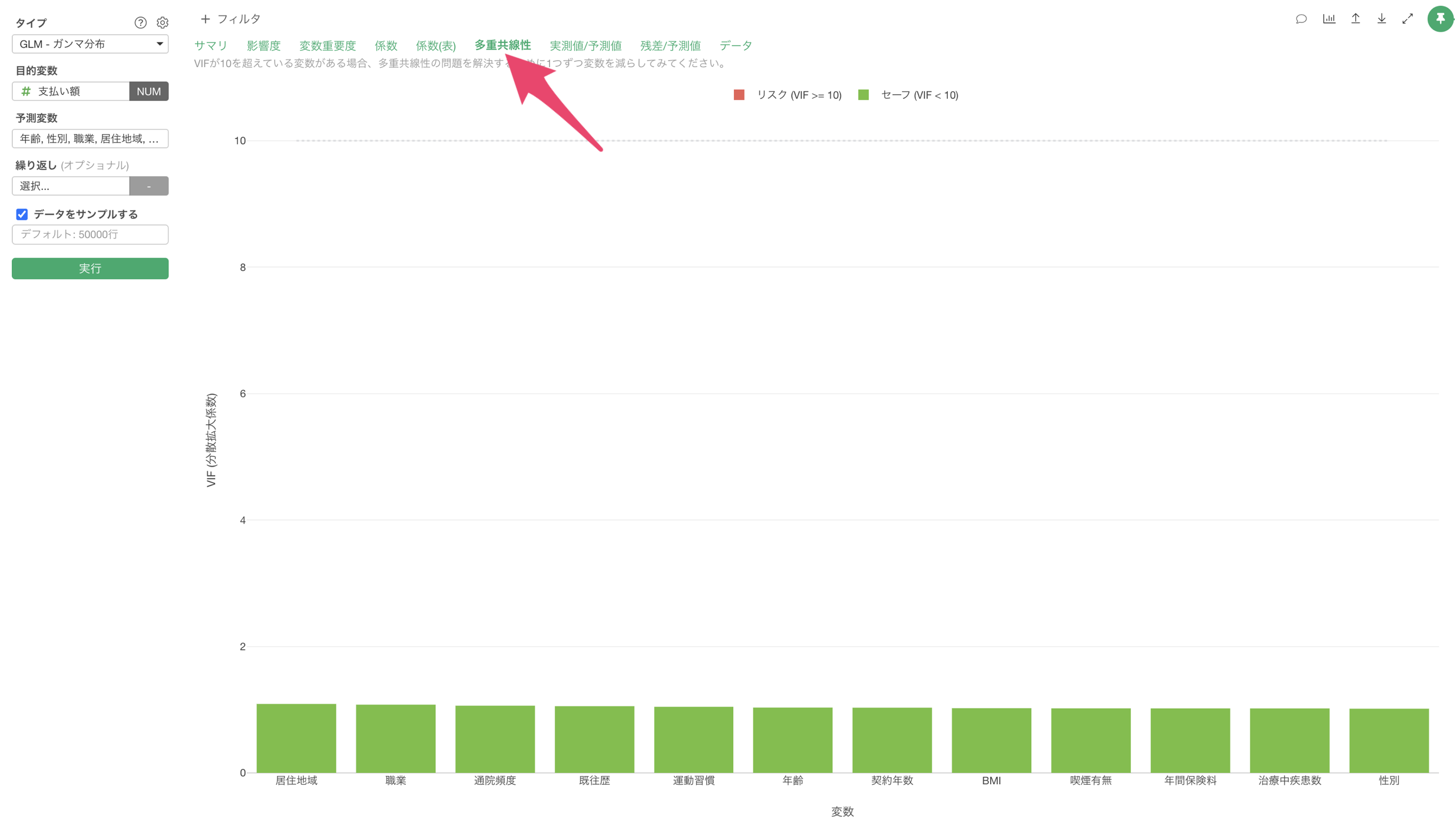
今回の結果は、VIFが10以上のものはないため、予測変数同士に相関が強すぎる変数の組み合わせがないため、モデルが不安定であることはないことがわかります。
変数重要度
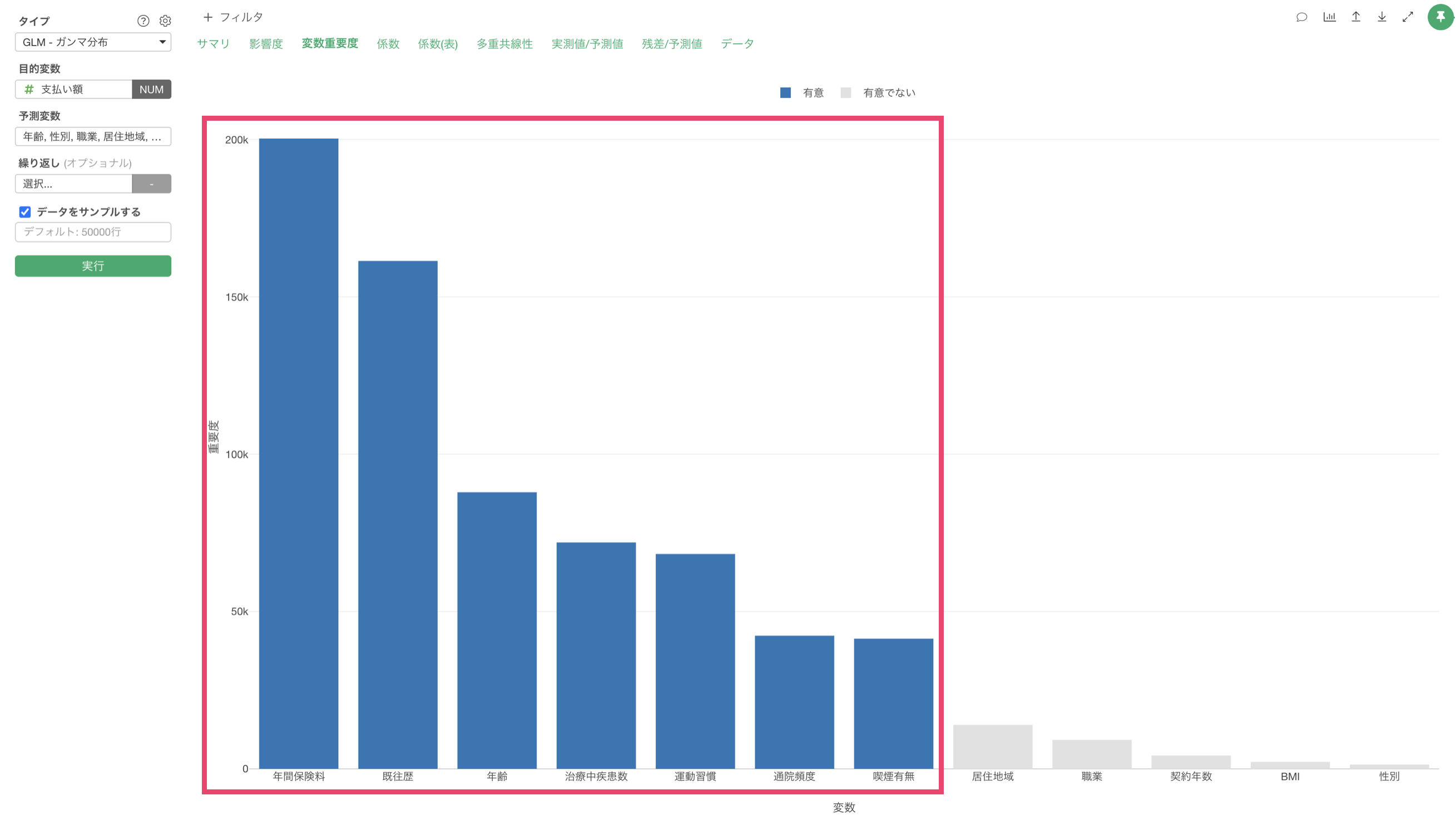
「変数重要度」タブをクリックすると、目的変数を予測する上でどの変数が重要なのかを確認することができます。
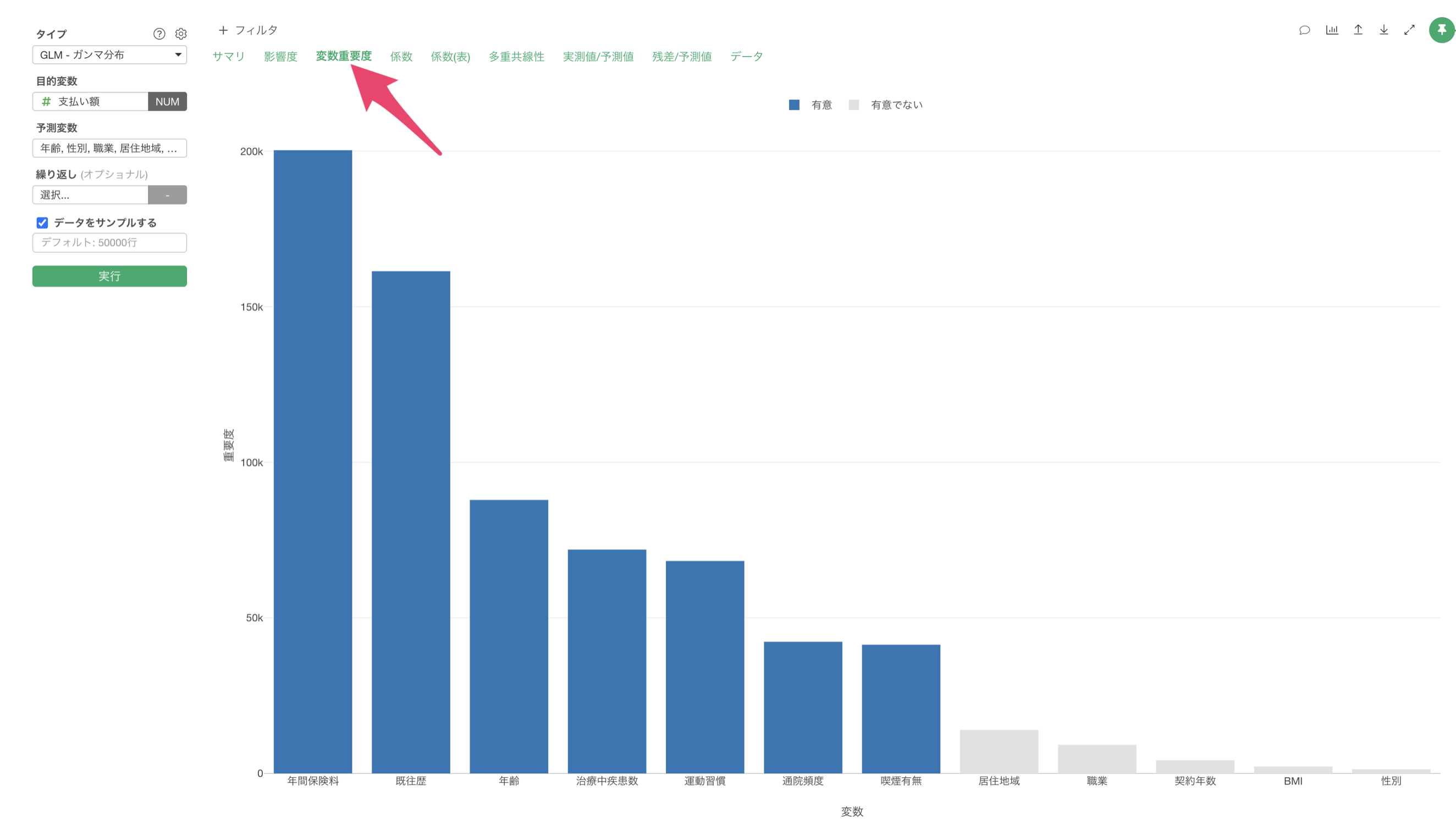
この結果から、支払額の予測に最も重要な変数は年間保険料であり、次いで既往歴、年齢の順となっていることがわかります。
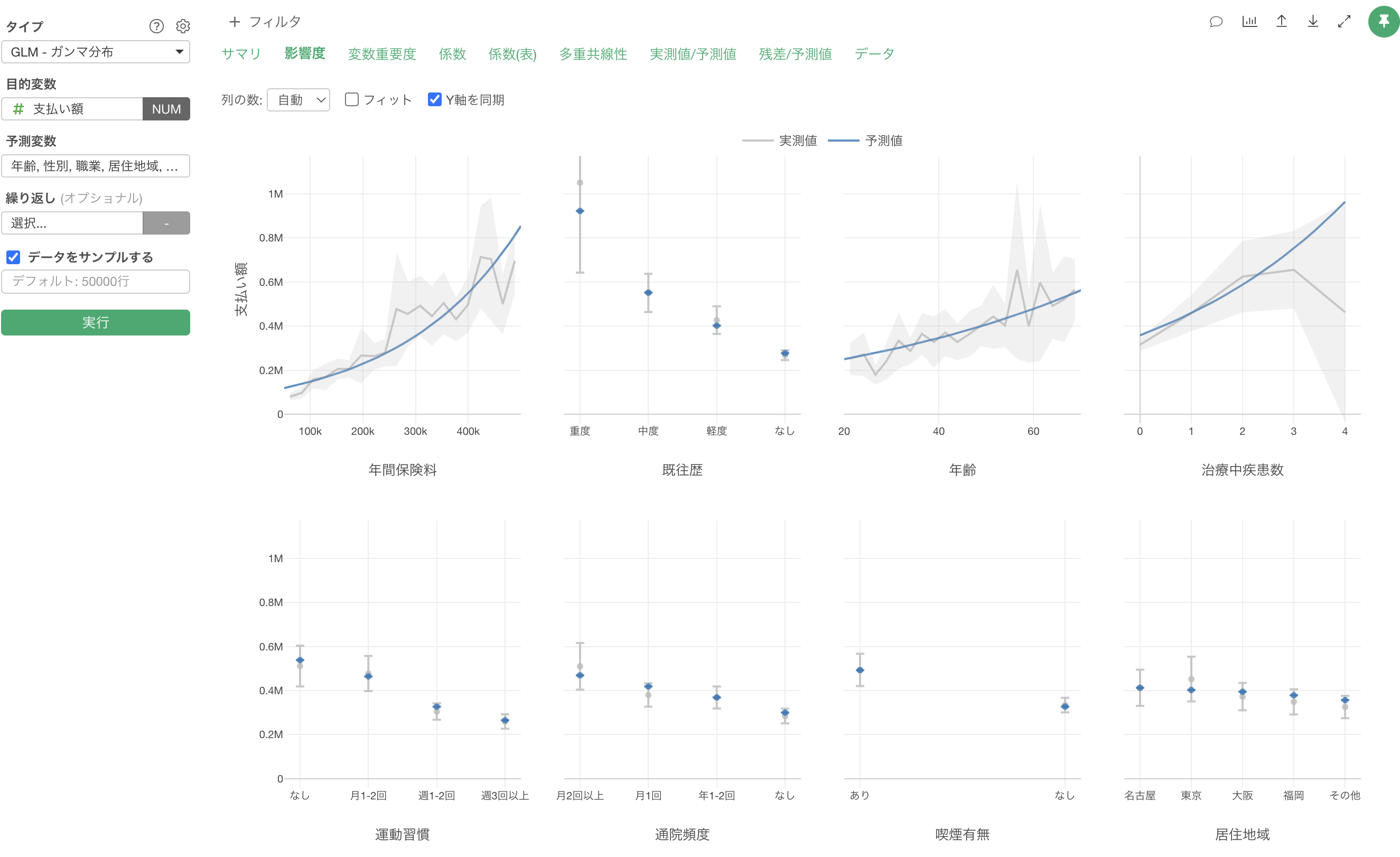
影響度
「影響度」タブでは、各予測変数が支払額に与える影響の方向と強さを確認することができます。
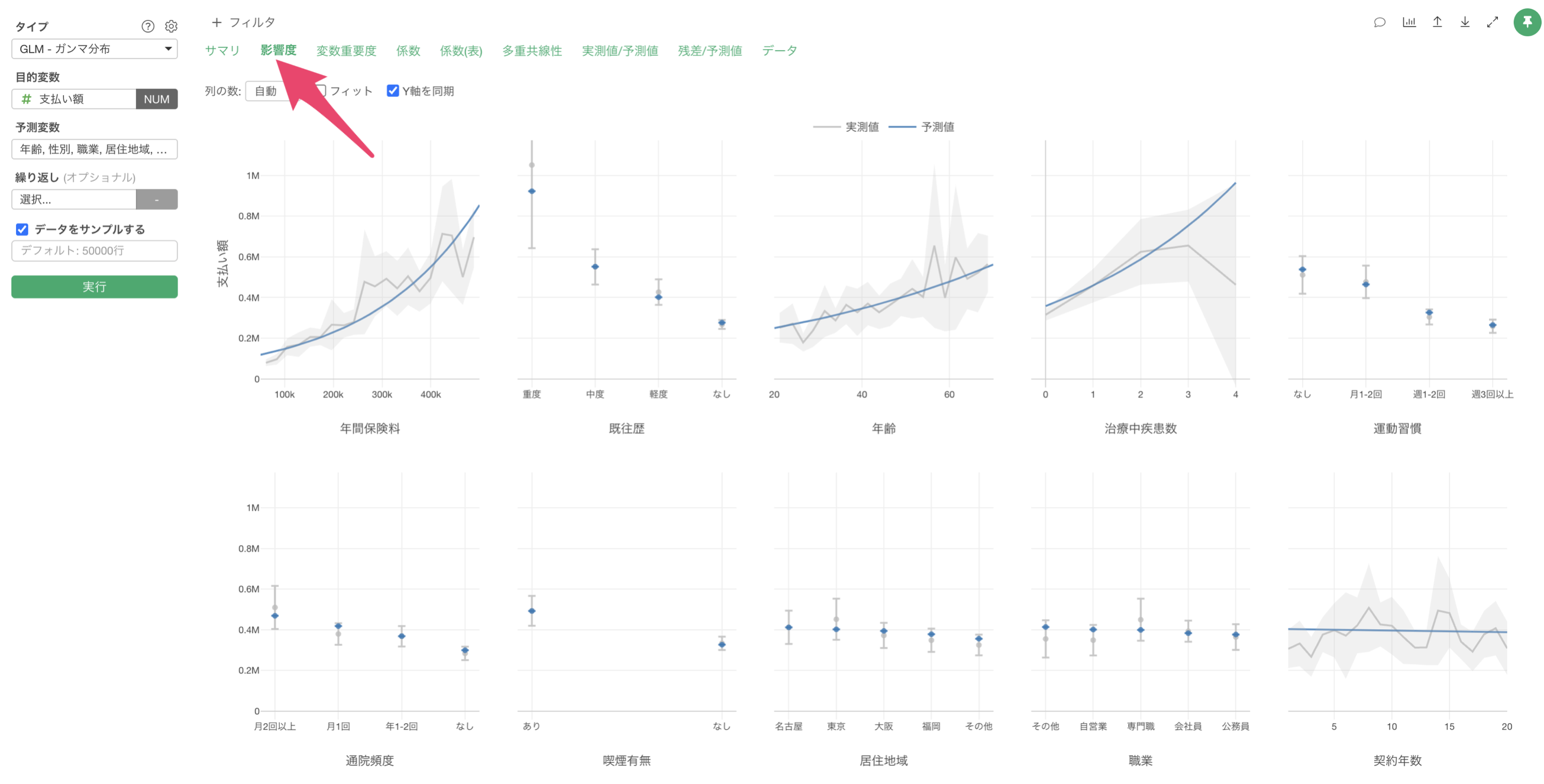
例えば、年間保険料の値が上がると、支払額も増えることが確認出来ます。
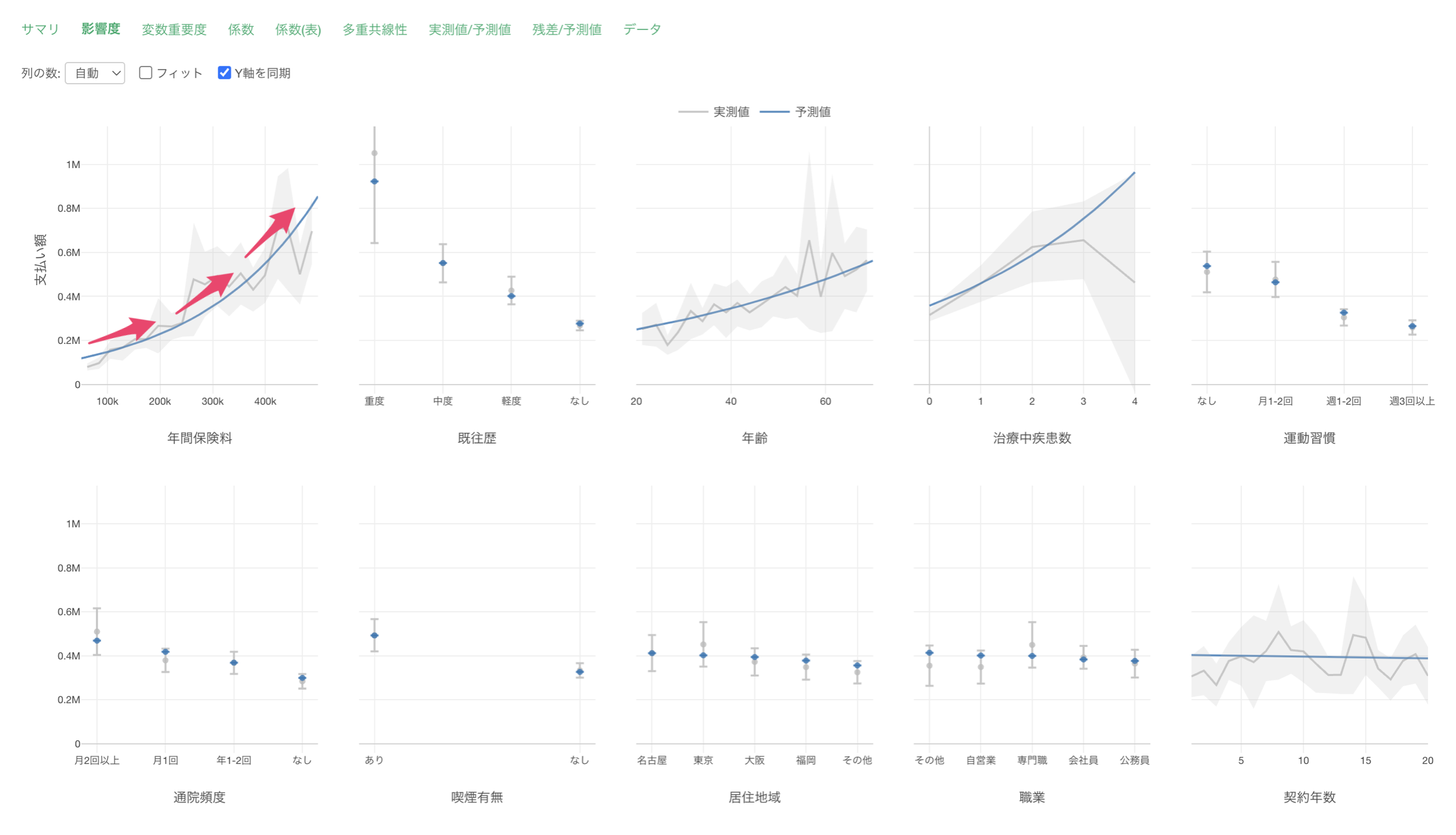
例えば、既往歴が重度の場合は、他に比べて支払額が高いことがわかります。一方で既往歴がなしの場合は、支払額が低い結果となっています。
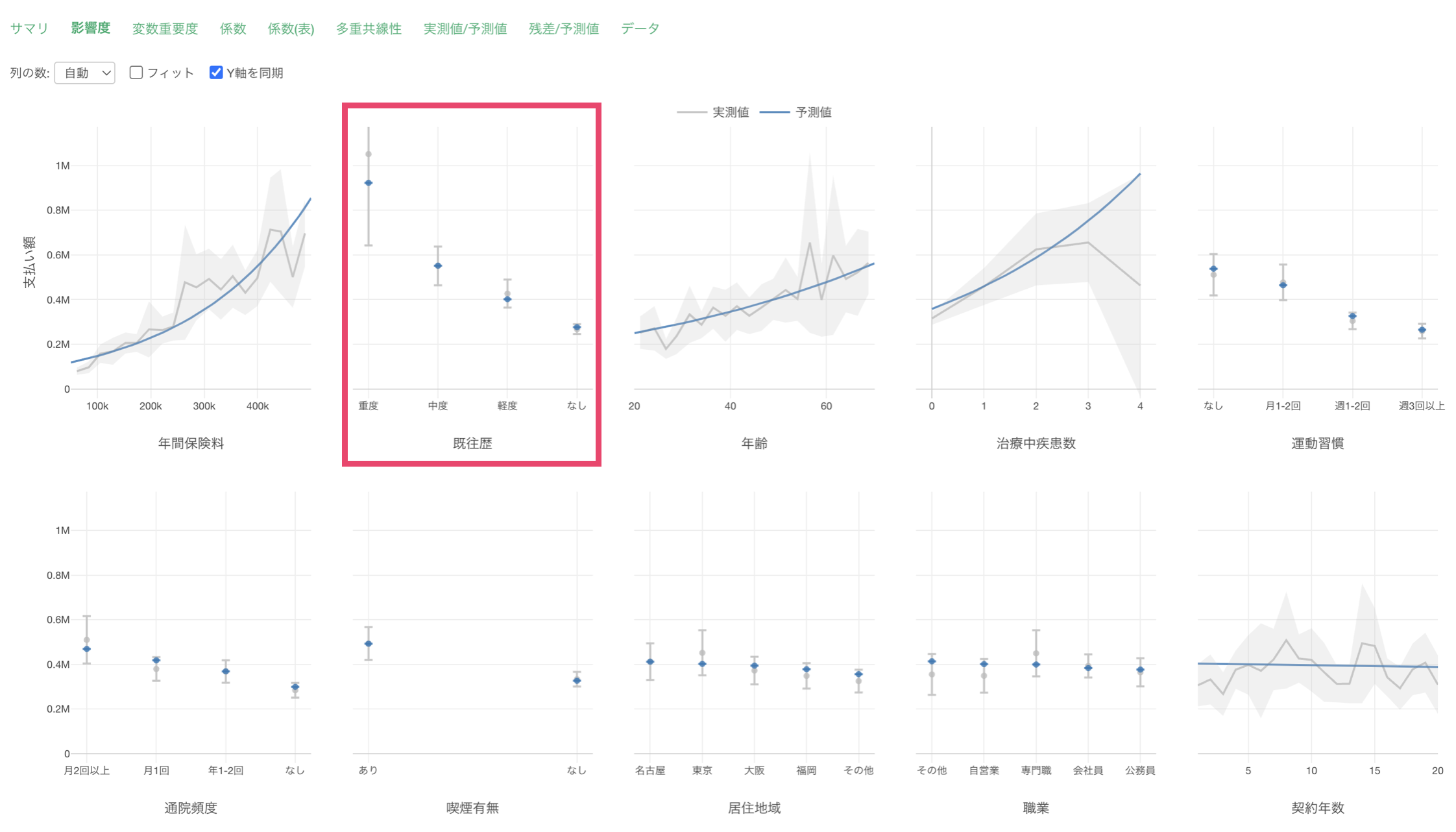
係数
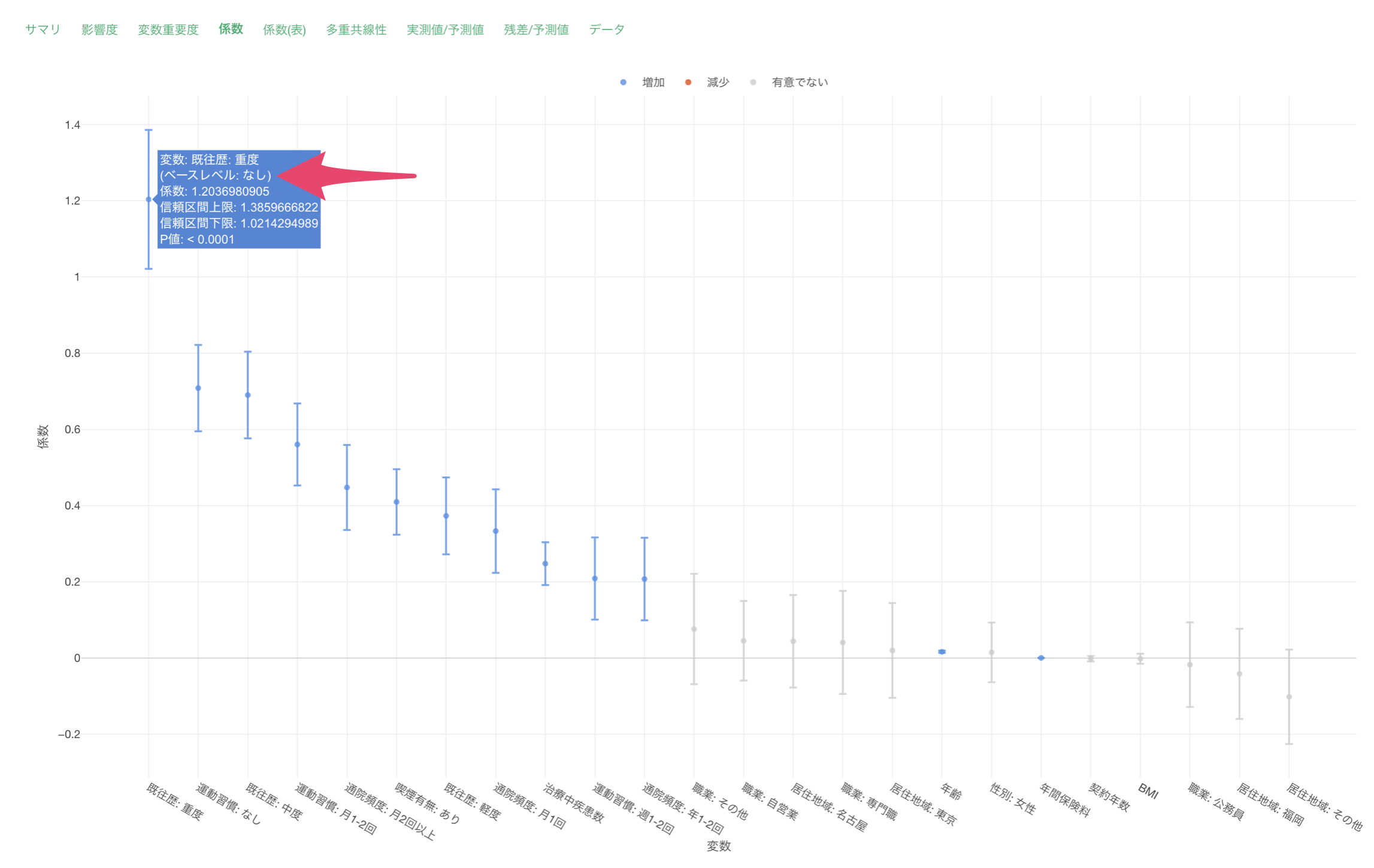
「係数」タブでは、各予測変数の係数とその統計的有意性を確認することができます。
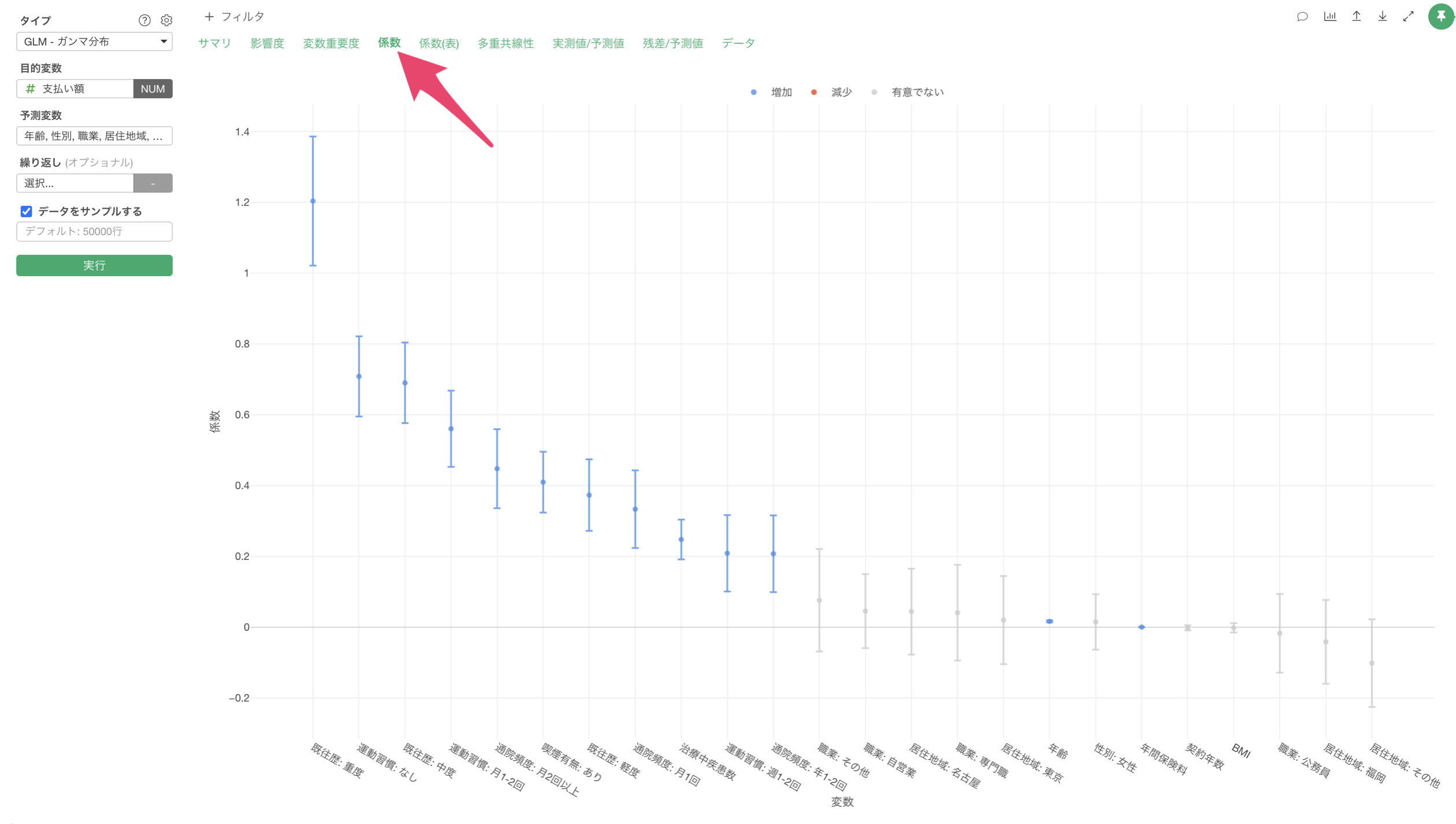
この結果から、各変数の効果の大きさを数値で確認できます。また、P値が0.05未満の変数は、統計的に有意な影響を持っていると判断できます。
ガンマ分布GLMでの係数は、対数リンク関数を使用しているため、解釈をする時には以下のようにします。
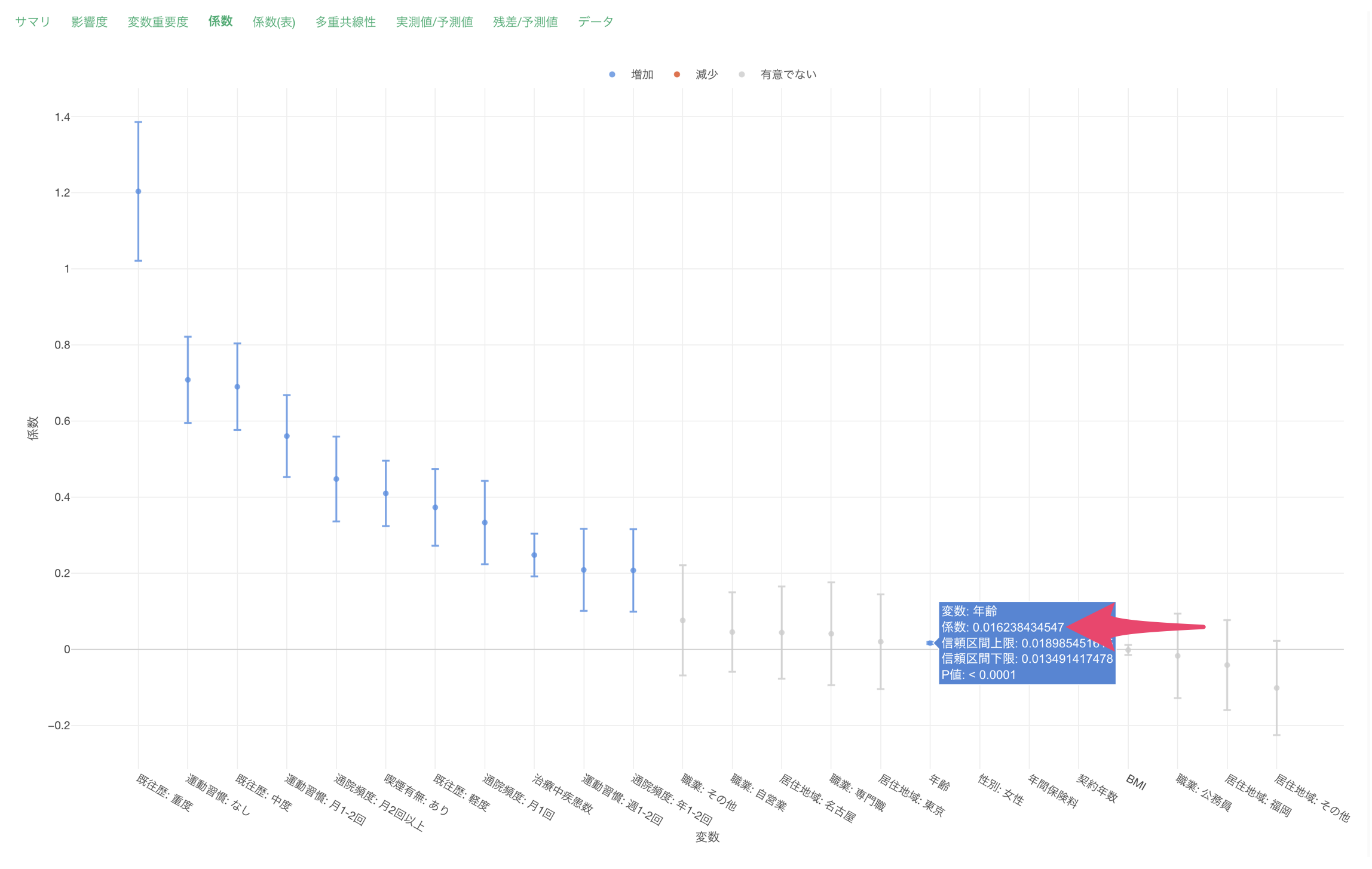
年齢の係数が0.016238であることは、「他の条件が同じ場合、年齢が1歳上がるごとに支払額が約1.6%増加する」ことを意味します。
- 係数の指数を取る: exp(0.016238) = 1.016
- この値から1を引く: 1.016 - 1 = 0.016
- パーセンテージに変換: 0.016 × 100 = 1.6%
既往歴の10度での係数が1.2037であることは、「他の条件が同じ場合、既往歴がなしと比較して重度の場合、支払額が約233%増加する」ことを意味します。
- 係数の指数を取る: exp(1.2037) = 3.33
- この値から1を引く: 3.33 - 1 = 2.33
- パーセンテージに変換: 2.33 × 100 = 233%
サマリ
「サマリ」タブをクリックすると、モデル全体の予測精度を確認することができます。

逸脱度の減少率
モデルが説明変数を加えることで予測精度改善しているかを表す指標で、値が大きいほど、モデルの説明力が高いことを意味します。
逸脱度減少率=Nullモデルの逸脱度−残差逸脱度Nullモデルの逸脱度×100 = 100逸脱度減少率=Nullモデルの逸脱度Nullモデルの逸脱度−残差逸脱度×100
基準値:
- 20%以上:とても良い
- 10-20%:十分な改善
- 5-10%:ある程度の改善
- 5%未満:改善が小さい
今回の場合は以下のように計算ができ、63.27%の減少は、予測精度が大きく改善したことを示しています。
(1055.61987056711 - 387.726042368186) / 1055.61987056711 × 100 = 63.27%4. まとめ
一般化線形モデル(GLM - ガンマ分布)は、保険金支払額のような0以上の小数を含む数値データの分析に適した手法です。特に、平均が大きくなるほど分散も大きくなるような現象を適切にモデル化できます。
今回の分析では、年間保険料、既往歴、年齢といった要因が支払い額に大きな影響を与えていることが明らかになりました。また、運動習慣や喫煙といった生活習慣も支払い額に一定の影響を与えていることがわかりました。このような分析結果は、リスク評価や保険料設定の改善に活用できることが考えられます。
参考資料
- アナリティクス・ギャラリー - リンク