A:この会社の給料のデータを見てたら男女間に差があるのがわかりました。
B:どれくらいの差があるの?
A:300ドルくらいの差があるんです。
B:なるほど、でも300ドルくらいだったら大した違いじゃないんじゃない?
A:いえ、やはり違いがあるにはあるので、これはレポートするべきだと思います。
B:でもちょとした違いがあるからっていちいちレポートしてたら、レポートすること多くなりそうだね。データはばらつくんだから、実は違いがないはずでも、実はちょっとした違いが出るなんてことはよくあることだよ。
A:それでは、どうすればレポートするべき違いがあるかどうか判断できるのですか?
B:こういうときには、t検定という仮説検定の手法が使えるよ。
t検定の基礎
t検定とは。。。
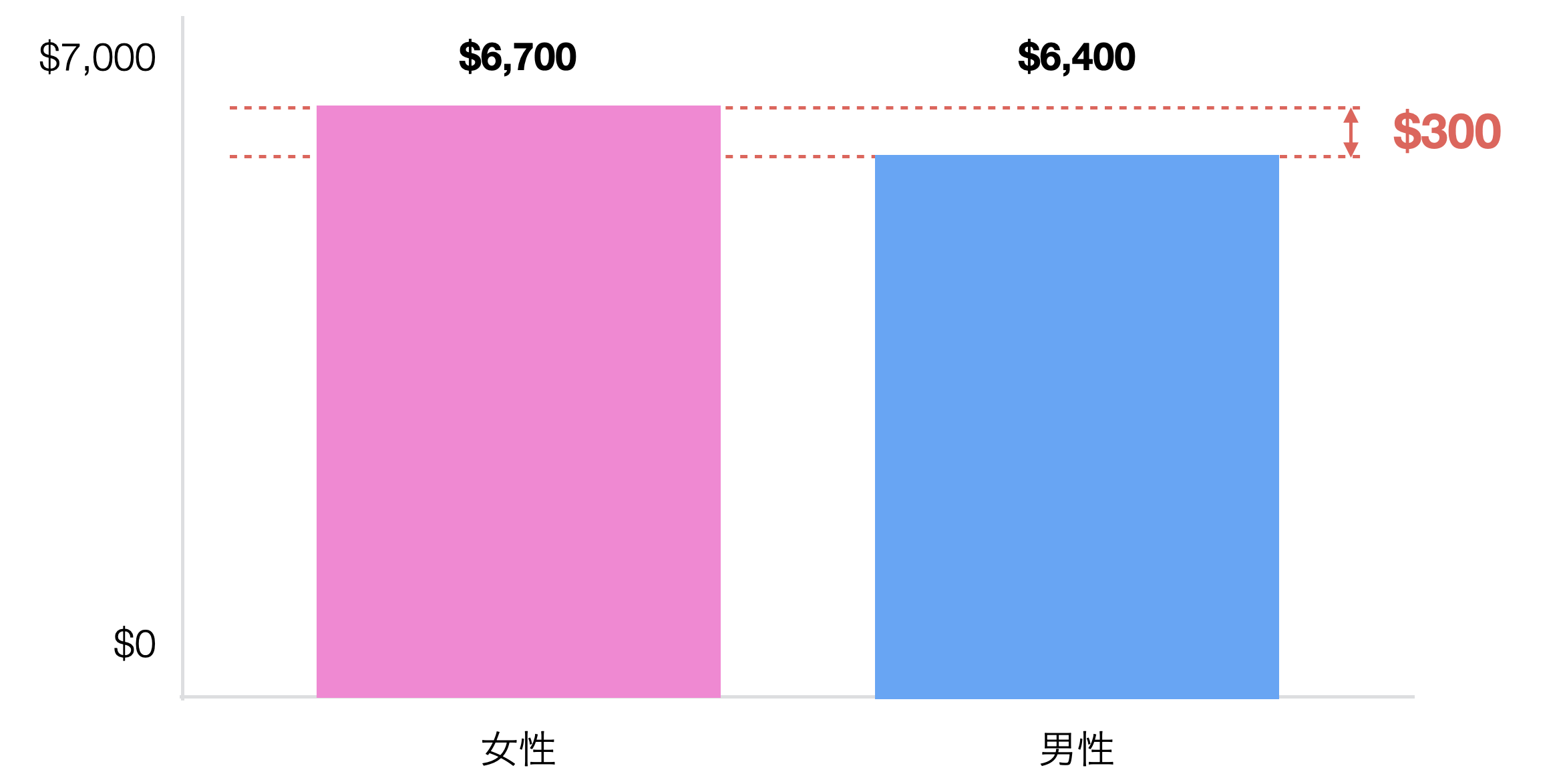
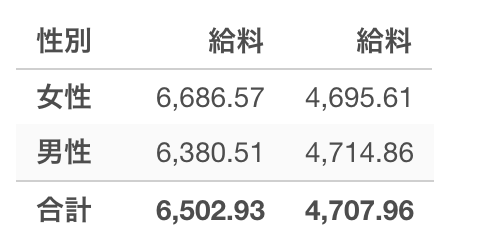
例えば今回の従業員データを使って男女間の給料の差について見てみると、女性の平均給料は6700ドル、男性は6400ドルで女性の方が多いことがわかりました。
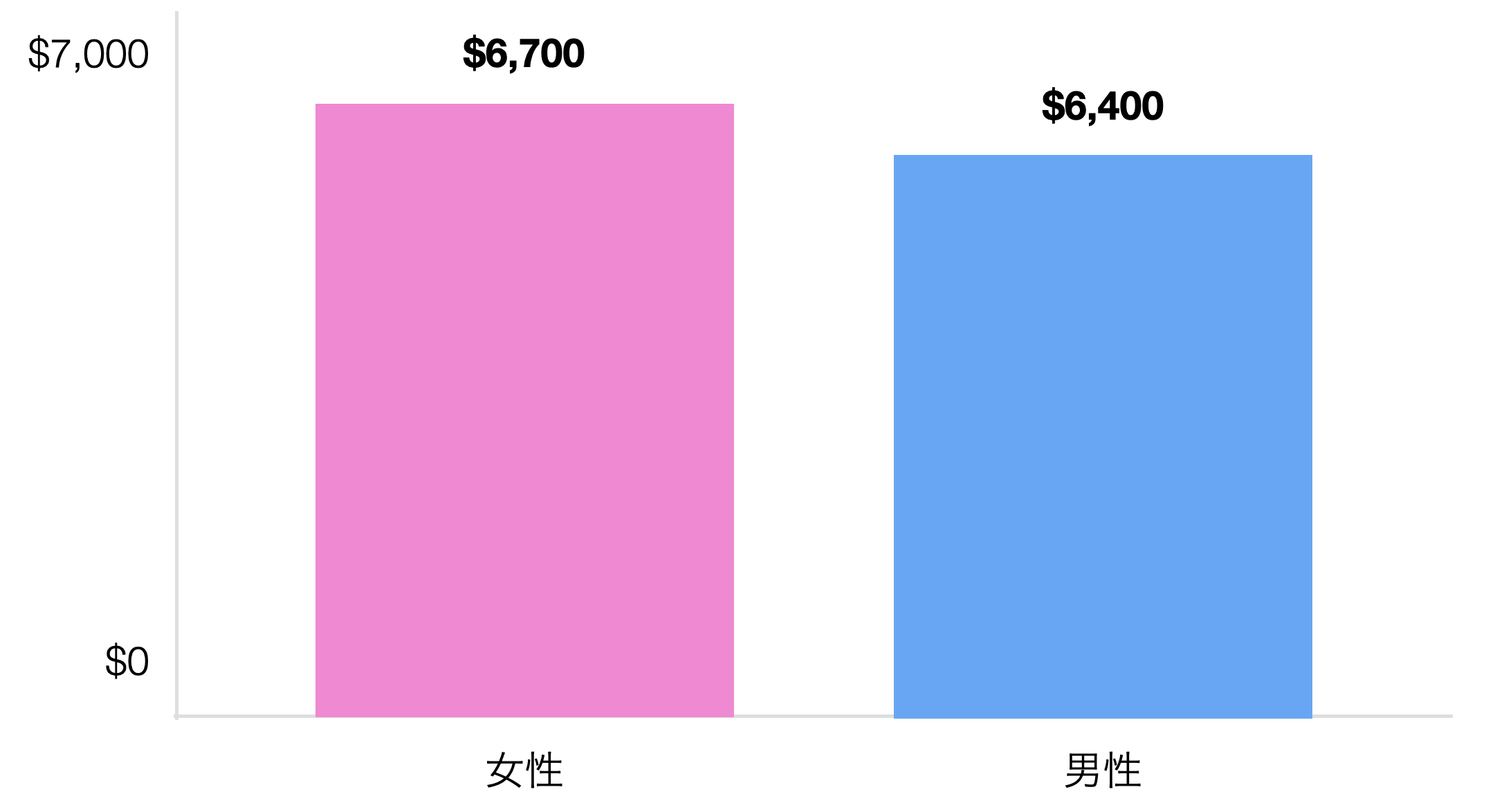
その差は300ドルなのですが、この違いを持ってこの会社では女性の方が給料が高いと言い切ってしまっていいのでしょうか。
そもそもデータはばらつくわけですから、それぞれの給料の分布も見てみましょう。
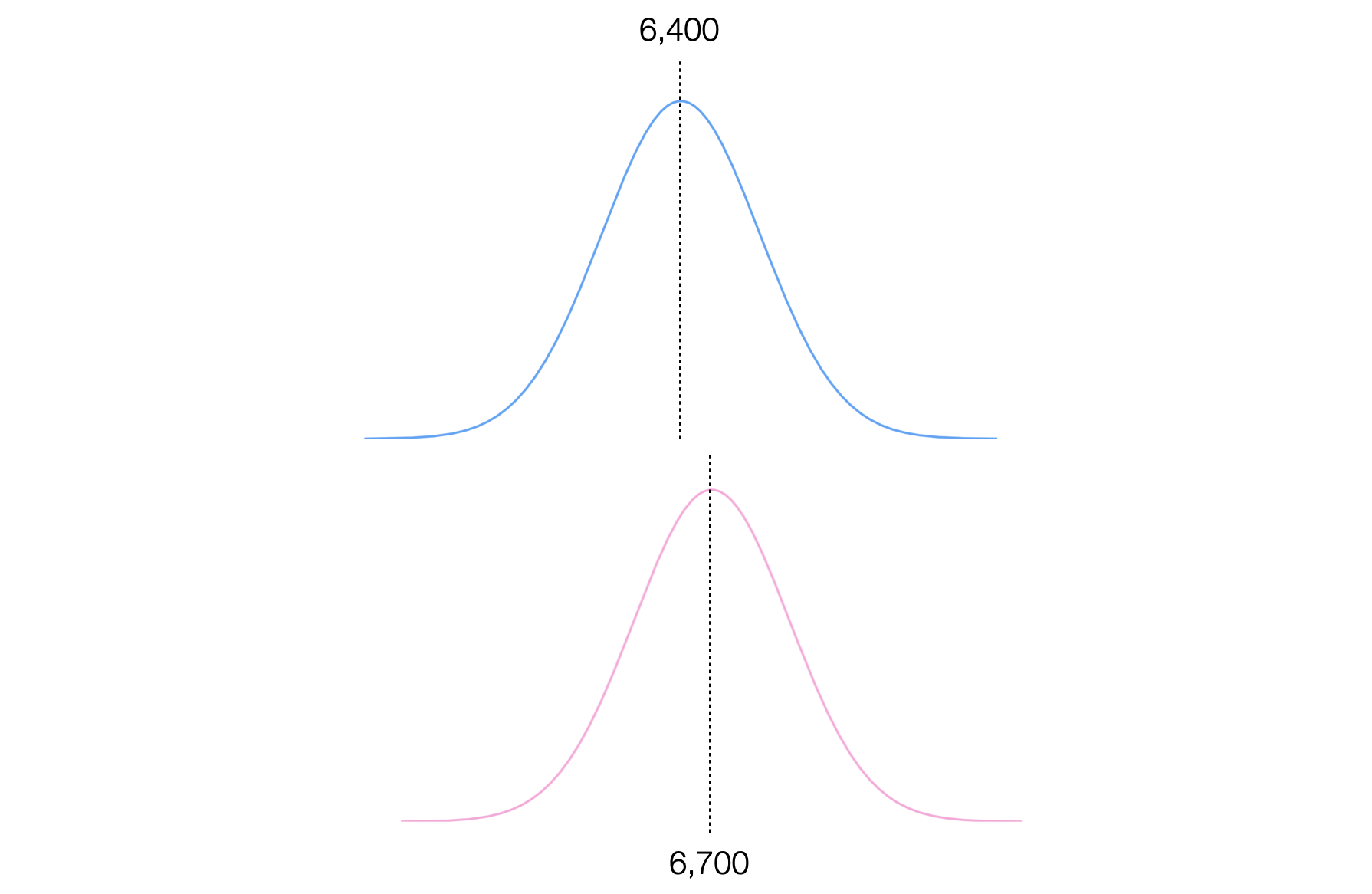
データの分布を比べるとあまり違いがないようにも見えます。しかし平均給料には300ドルの違いがあるというのも事実です。
そこで、この300ドルというのが違いがあると判断できるほど大きな違いなのかどうか、これを調べたい、その場合どうしたらいいでしょうか?
ここで仮説検定が使えるのですが、今回のように2つのグループ間の平均値の違いが有意なのかどうかを判断するには一般的にはt検定という検定手法を使うことができます。
しかし実はt検定にはいくつかのタイプがあります。広く使われているのはウェルチのt検定と言われる手法で、ここでも先ほどの男女間の給料の平均値の差が有意なのかどうなのか判断するためにもウェルチのt検定を使うことになるのですが、いきなりウェルチのt検定の話をするとすこし複雑なので、まずは他のタイプのt検定を見て行ってみましょう。そうすることで、t検定における考え方、その仕組みをより理解できるようになり、最終的にはウェルチのt検定の仕組みや背景もより深く理解できるようになると思います。
そこで、以下の順で解説していきたいと思います。
- Z検定
- 1つのサンプルのステューデントt検定
- 複数のサンプルのステューデントのt検定
- ウェルチのt検定
Z検定
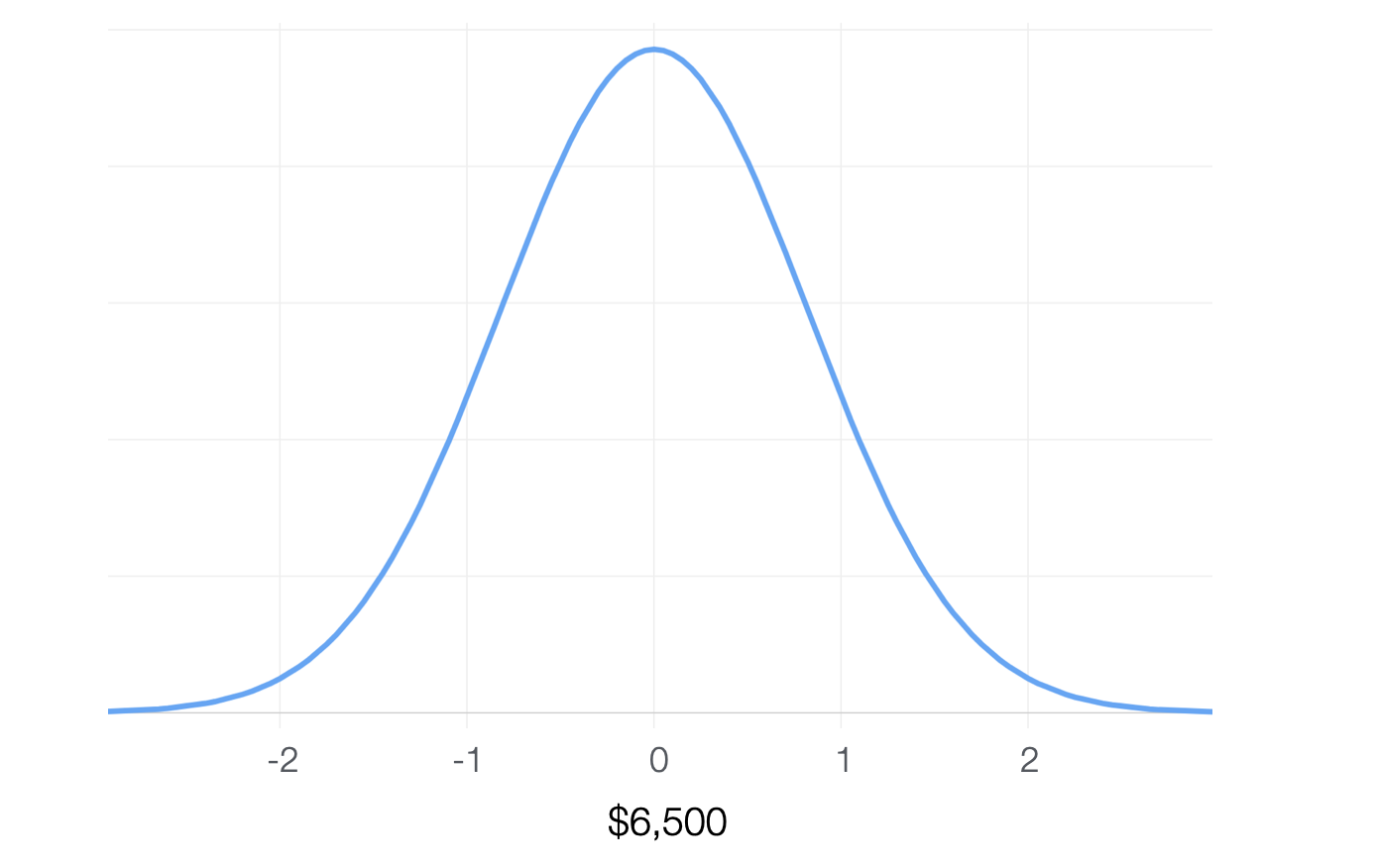
例えばこの会社の全体の平均給料は6500でした。そしてその中から女性の人たちだけをとってきてその平均給料を調べると6700ドルでした。この場合この6,700ドルは高いと言えるのでしょうか。つまり女性だから給料が高い、または小さいと判断できるのでしょうか。
手元にデータがあり、その平均値と標準偏差がわかっています。その場合に、この平均値は母集団の平均値と比べてどれだけ大きいのかどうかということです。
ここで使えるのがZ検定というものなのです。
帰無仮説
まずここでの帰無仮説は、手元にあるデータの平均値が母集団の平均値に差がない、つまり違いがないというものになります。ということは手元にあるデータは母集団からサンプルされたうちのデータの一つにすぎないということです。
ここで中心極限定理の話を思い出してみましょう。もし同じ母集団から何度もサンプルを繰り返したとするとそれぞれのサンプルから得られた平均値の分布は、ある程度のデータがあれば、正規分布の形になるという話をしました。
そしてこの分布のばらつきの指標のことを標準誤差と呼び、この標準誤差を±1.96倍したものが95%信頼区間の幅となるという話をしました。
ということは同じ母集団から何度も繰り返しサンプルするとそれらの平均はいつも母集団の真の平均であるとは限りませんが、それでもその平均から±1.96の間に95%の確率で収まるだろうと推定されます。
なのでもし帰無仮説が正しいのであれば、手元にあるデータの平均値はこの95%区間の間に入っているであろうと想定することができます。もしこの区間の外にあるなら、つまり1.96よりも大きい、または-1.96よりも小さいのであれば、P値の有意水準を5%とするのであれば、起きえないことが起きているということになります。
以下は両側合わせてその5%となる領域にハイライトしたものです。
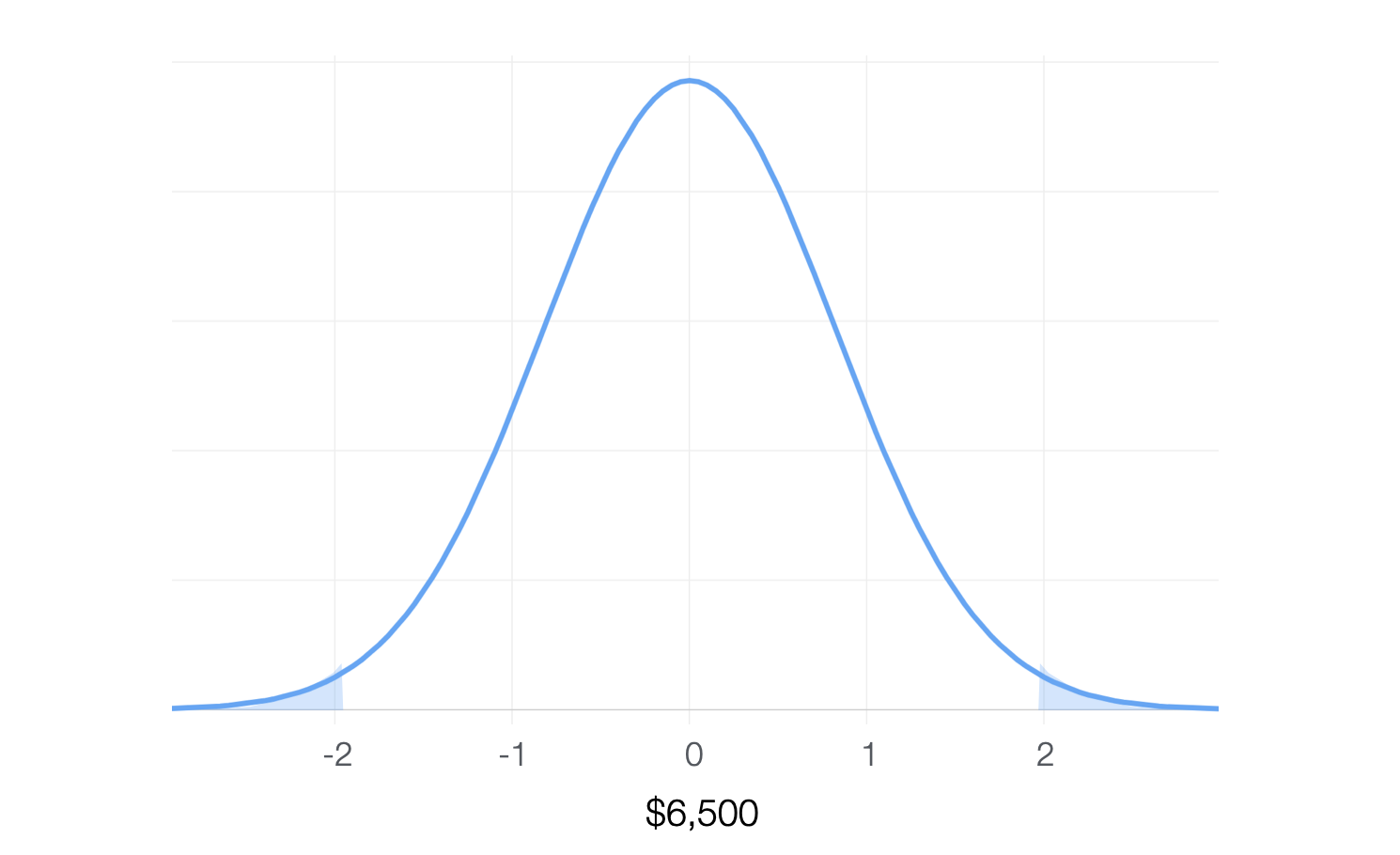
そこで手元のデータの平均値である6700ドルがこの分布のどこに来るか。そのためにはこの6,700ドルという数値を標準化すればいいですね。そしてその標準化された数値が1.96よりも大きいのであれば、それは5%以下でしか起きえないということで、帰無仮説を棄却できます。そのためにこの手元のデータから得られた平均値をそれが属するであろう平均値のばらつきをもとに標準化します。ここでのばらつきとは標準誤差になります。
ここでよく標準偏差と標準誤差の区別がつかなくなる場合があるので、一度整理しておきます。標準偏差は手元のデータのばらつきの指標です。ここでのばらつきとは1つのサンプルそのものの中のばらつきです。
それに対して標準誤差とは、同じ母集団から何回も繰り返しサンプルを取ったさいの平均値のばらつきのことです。
そしてこの標準化した値のことをこのZ検定ではZ値と呼びます。
Z値 = サンプル平均値 - 真の平均値 / 標準誤差そして標準誤差は、信頼区間の章で見たように手元の標準偏差をもとに中心極限定理を使って1/sqrt(N)倍小さくなるわけですから以下のように求めることができます。
標準誤差 = 標準偏差 * 1/sqrt(N)今回の例ですと、手元のデータの平均値が6700、全体の平均値が6,500なので、以下のような式でZ値を算出できます。
Z値 = (6700 - 6500) / 標準誤差 = 200 / 標準誤差手元のデータの標準偏差は4,700で、データ量は900行なので、標準誤差は以下のような式で算出できます。
標準誤差 = 4700 * sqrt(900) = 141,000そこでZ値は1.2765となります。
Z値 = 200 / 141,000 = 1.27651.27は1.96よりも小さいですね。チャートで見ると、以下のようになります。
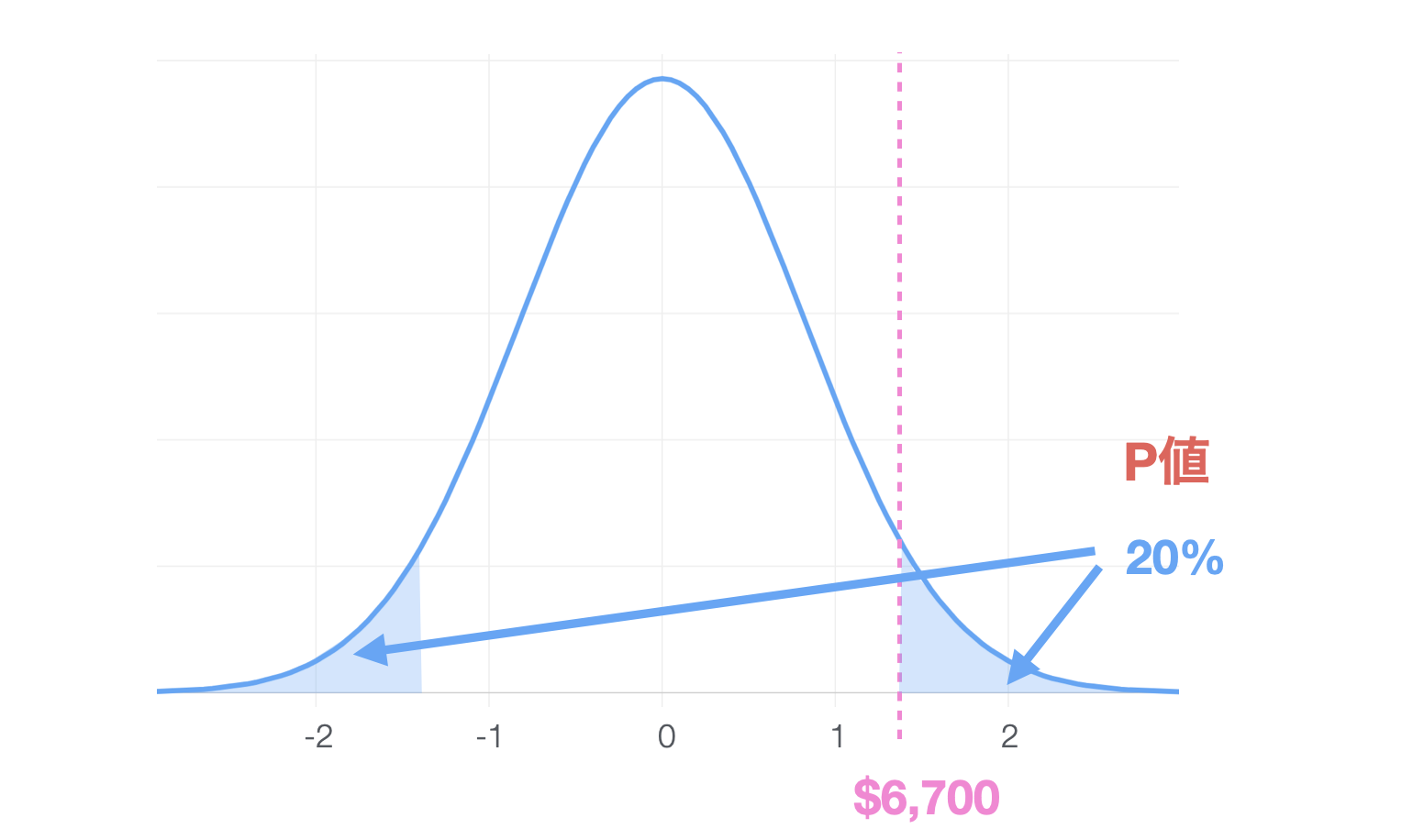
有意となるであろう領域よりも真ん中に近い方です。するとこの6700ドルかそれ以上に大きな数値、またはそれと対応する全体の平均値とは逆の小さい方として6300ドルかそれ以下に小さい数値がえられる確率は20%となりました。
そこで、有意水準が5%だとすると、この手元にあるデータの平均の6700ドルくらいであればよくあるばらつきだと考えられるわけですから、帰無仮説である「手元のデータの平均値と母集団の平均値に差はない」を棄却できません。
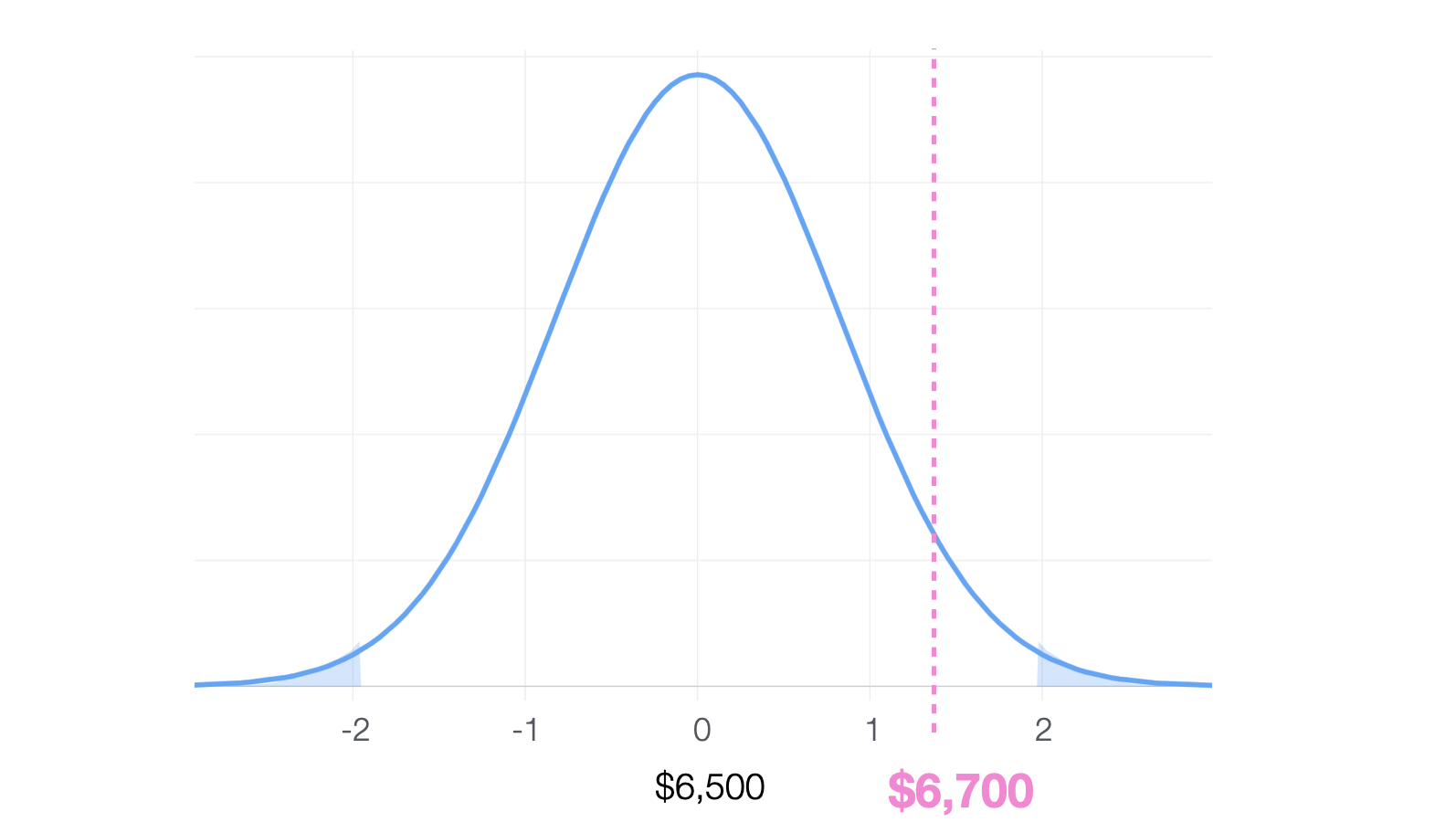
つまり結論としては違いがあるとは言えないとなります。
これがZ検定と言われるもので、ここではその確率分布として正規分布が使われました。これはある程度のデータがあればその平均値の分布は正規分布の形になるという中心極限定理によるものです。
さてここで注意しなくてはいけないことがあります。それはこのZ検定を使う際の以下の前提条件です。
正規性 - 分布が正規分布であるというものです。今回は平均値の分布が正規分布になるという仮定でしたので問題ありません。しかしもしデータが例えば10行くらいしかないのであれば、その平均の分布が正規分布となるとは限りません。それは母集団のデータの分布がどのような分布なのかによっても変わってきます。
独立性 - それぞれの行のデータが独立して母集団から抽出されていること。これは普通のデータであれば大抵の場合問題とはなりません。問題になるのは同じデータを何度もコピーして作られた場合に、例えばジョンという同じ従業員の行が何度も入っている場合などです。
標準偏差が既知である - 母集団の真の標準偏差がわかっている。今回は手元のデータの標準偏差からサンプルの平均の分布の標準誤差を算出しましたが、これは手元のデータと母集団が同じばらつきの大きさだと仮定していることになります。しかし、そもそも手元のデータの平均値と母集団の平均値が違うのではないかと疑うからこの検定をしているにも関わらず、標準偏差は同じだというのは変です。そうであれば、母集団の標準偏差がわかっているというのも嘘となります。
これが、ほとんどの場合においてZ検定が使われることはない理由です。そこでt検定が使われることになるのです。
t検定
a guy called William Sealy Gosset (Student 1908), who was working as a chemist for the Guinness brewery at the time (see Box 1987). Because Guinness took a dim view of its employees publishing statistical analysis (apparently they felt it was a trade secret), he published the work under the pseudonym “A Student”, and to this day, the full name of the tt-test is actually Student’s t-test.
ここで中心極限定理の話を思い出してみましょう。もし同じ母集団から何度もサンプルを繰り返したとするとそれぞれのサンプルから得られた平均値の分布は、ある程度のデータがあれば、正規分布の形になるという話をしました。そしてその分布のばらつきの指標のことを標準誤差と呼び、この標準誤差を±1.96倍したものが95%信頼区間の幅となるという話をしました。
さて、この標準誤差の算出の仕方はこの後にみるとして、まずはt検定の仕組みの理解を進めましょう。
ゴセット氏が発見した重要なことはどうすれば真の標準偏差が何であるかがよくわからないという事実を考慮した上で検定を行うことができるかということです。
そこで母集団の標準偏差がわからないのであれば、手元のデータの標準偏差から推定しようということになります。Z検定のときはZ値という統計量を使っていましたが、t検定ではt値という統計量を使います。しかし考え方は同じです。真の平均値からの差を標準誤差で標準化した値です。ですので式はほぼ同じです。
t値 = サンプル平均値 - 真の平均値 / 標準誤差そしてこの標準誤差を求める式もZ検定の時と同じです。
標準誤差 = 標準偏差 * 1/sqrt(N)ただここで唯一違うのは標準偏差の計算です。Z検定におけるZ値の計算には母集団の標準偏差が使われていたのに対し、ここではサンプルの標準偏差を元にした母集団の標準偏差を推定した値です。そしてこの推定された標準偏差はNの代わりにN-1で割ることになります。
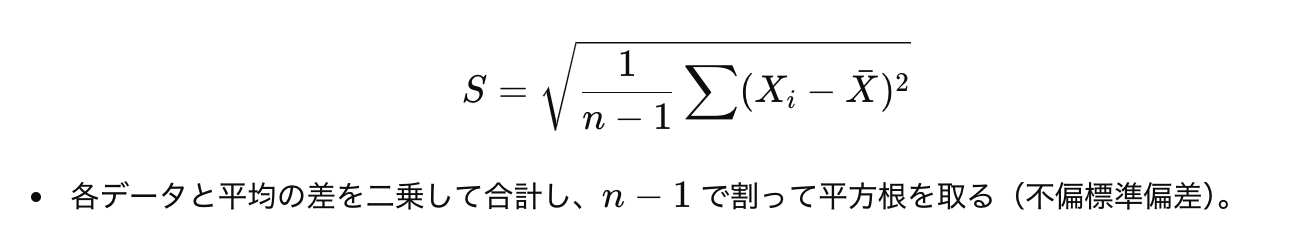
標本データから母集団の分散を推定する際、単に標本の平方和の平均(標本分散)を使うと、「母分散の期待値が過小評価される(バイアスがかかる) 」という問題があります。
そのため、標本の分散を計算する際に 「不偏分散(unbiased variance)」 を求めるために、分母をN−1 にする補正が必要になります。
自由度
さてこの自由度ですが、なんだかややこしそうな言葉です。まず、統計学の手法を使ってデータを分析していく際にはほぼ気にすることはありません。ただ、特に仮説検定の道具とも言える確率分布の定義を理解する際に出てきますので、ここで簡単に説明します。
まず、自由度とは、統計データにおいて 自由に変えられるデータの数 を表す概念です。簡単に言うと、「データの制約がない、独立して選べるデータの数」です。
例えば、3つの数値があってそれらの平均値を求める場合を考えてみましょう。その場合平均値を求める式は以下のようになりますね。
平均値 = A + B + C / 3さてこの場合、もしA、B、Cの合計が30だとすると、自由に選べるのは最初の2つの数だけとなります。というのも例えば、Aが10、Bが12だとすると、Cは自ずと8だと決まってしまいます。するとAとBの2つに関しては自由に数字を選べるが、残りのCはそうでないとして、この場合の自由度は2ということになります。
そしてこれはもし数値の数が10個だったときも同じです。合計が例えば100などと決まってしまえばその中で自由に選べる数字は9つだけで、最後の1つは自ずと決まってしまいます。
そこで、この場合の自由度を求める式は以下のようになります。
自由度 = 数値の数 - 1 このN-1という補正を入れることで、このt値はZ値と若干変わってきます。といってもデータ量が少なければ、気づくような違いとなりますが、ある程度のデータになるとほぼ違いはありません。Nが2のときであれば、2で割るか2−1の1で割るかは大きな違いとなりますが、Nが1000であれば1000で割るか999で割るかは大した違いではなくなります。
t分布という確率分布
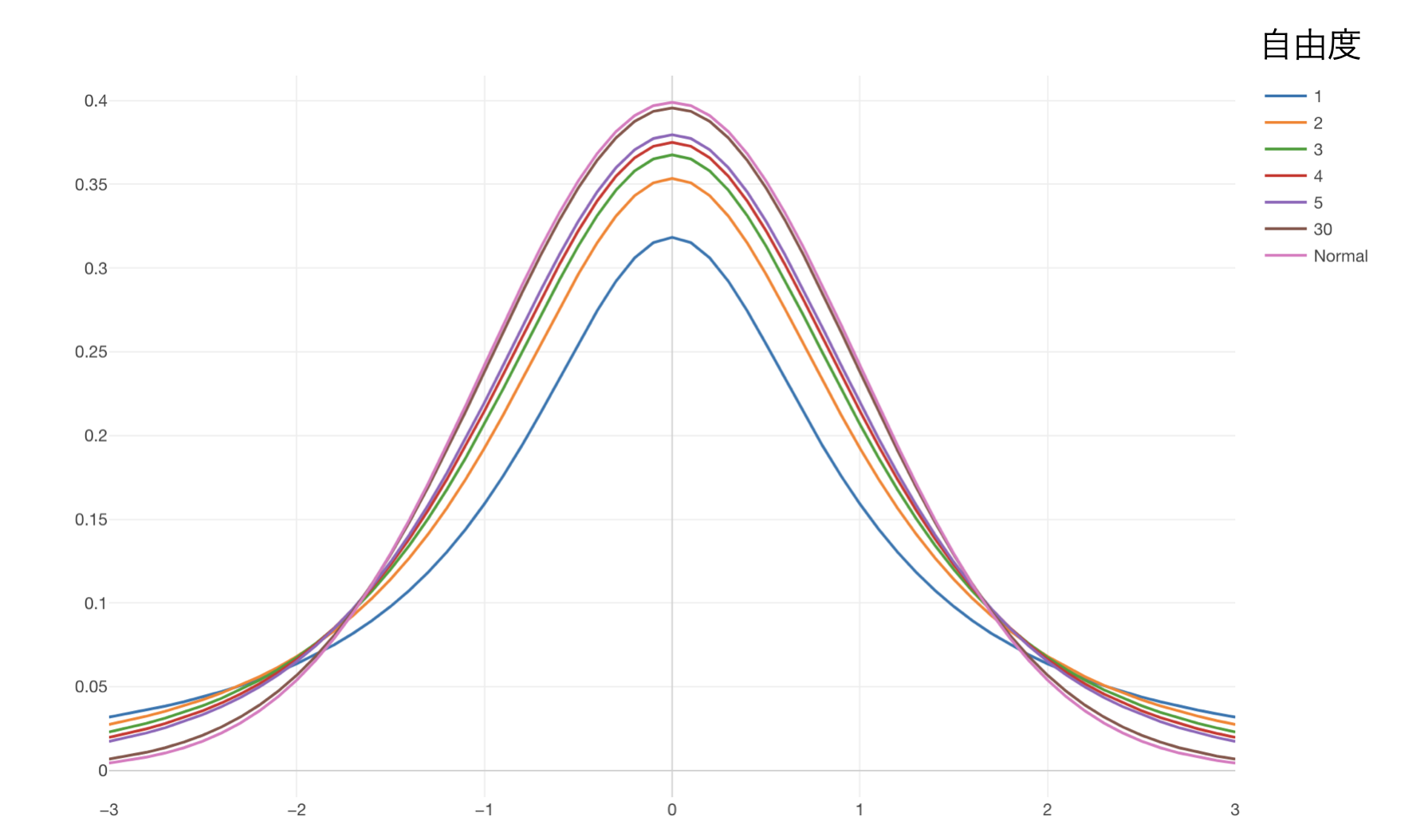
同じ母集団からサンプルを何回も繰り返し、このt値を算出すると、Z値が正規分布に従うように、そのt値はt分布という確率分布に従うということがわかっています。
ここでt分布とは何でしょうか?一見正規分布のように見えますね。それもそのはず基本的に正規分布と言ってもいいような分布です。
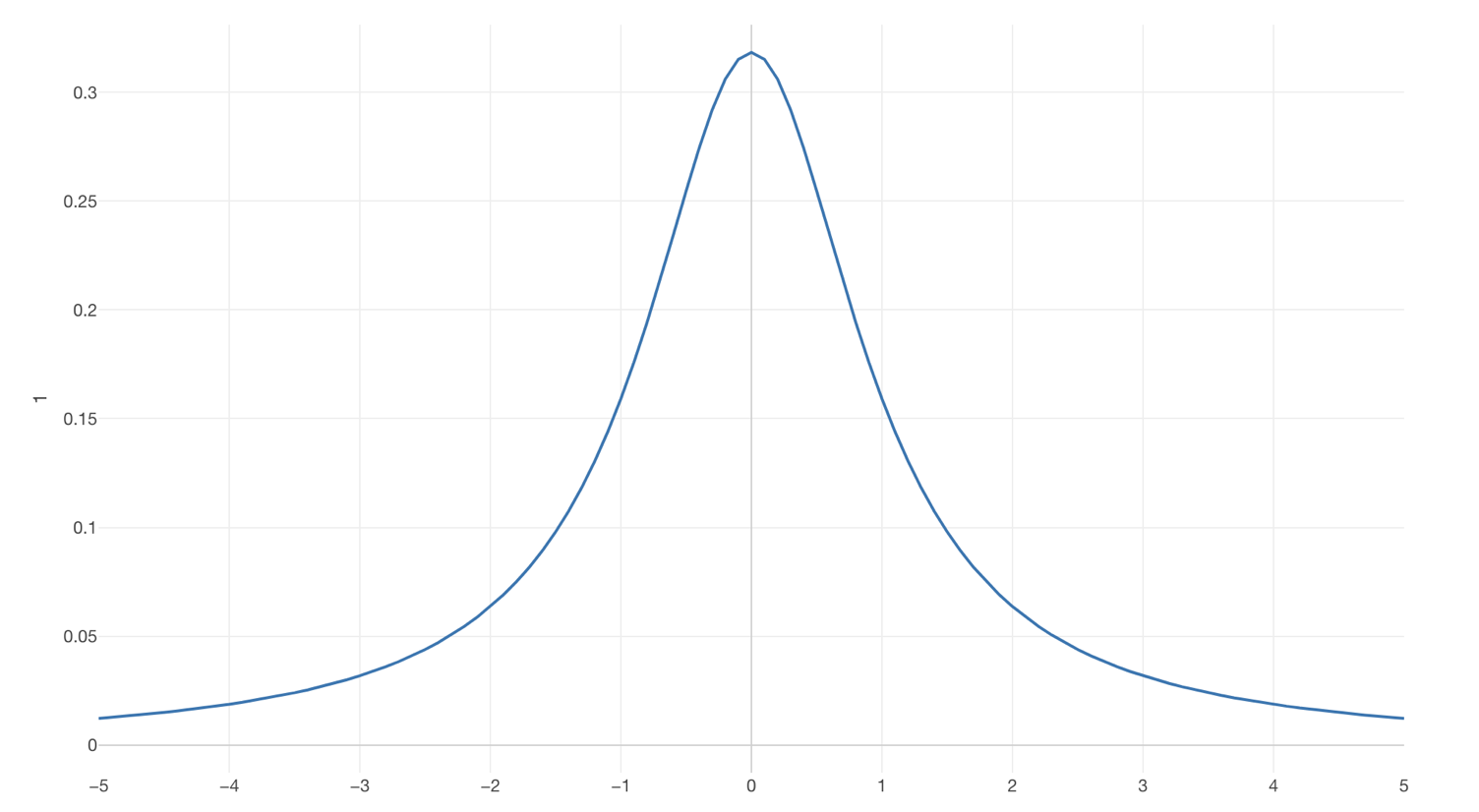
データが少ない時は裾野のあたりが正規分布に比べて少し太いかんじの分布なのですが、データの量がある程度になると正規分布となります。これはこのt分布を描くための式には自由度というパラメーターがあり、この値がデータの量によって変わるからです。
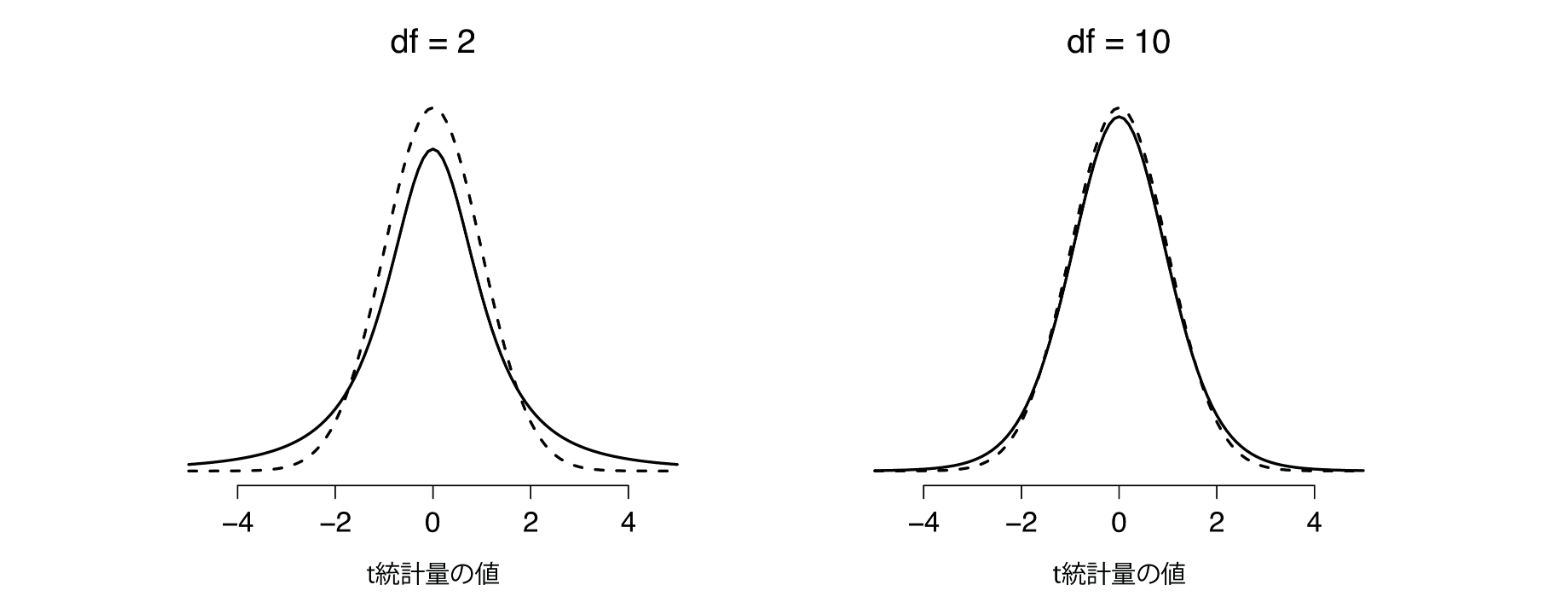
ここでの自由度はN-1です。ということは例えば1000行のデータがあったとすると自由度は999ということになります。
標本の標準偏差を元に推定された標準偏差を使うため、標本サイズが小さいと推定誤差が大きくなり、分布の両端の高さが高くなります。例えばt値が3だったとすると、もしデータが31行だとすると自由度は30となります。その場合、t分布はほぼ正規分布と同じような分布となりますが、t値が3のときその値がそれ以上の値が起きる確率というのは1%未満となります。しかしデータが3行しかなければ自由度は2なので、t値が3以上の値が起きる確率というのはさきほどよりも高くなります。
つまり母集団の標準偏差が未知であれば、それを推定せざるをえないわけで、その限りにおいてはデータが少なければその推定値自体のばらつきが大きくなり、データが多ければ逆にそのばらつきは小さくなるということです。これは中心極限定理が効くからですね。
データが少ない場合、正規分布であれば有意になっていたt値でも(例えばt値が2.5)、t分布の場合には有意とならないかもしれないということです。
つまり、t値が従う確率分布であるt分布はまさにこのデータが少ない場合の不確実性を加味した分布と言えるのです。
Let’s do it
それでは、実際にt検定を行ってみましょう。
私たちのウェブサイトを訪れた人たちのサイト滞在時間の平均は18分だということがわかっています。そして、統計学のページを訪れる人たちの滞在時間の平均は20分です。この違いは有意なのでしょうか。もし有意なのであればもっと統計学の記事を増やすといった施策を行うことになるかもしれません。しかし、この違いがただのデータのばらつきなのであれば、わざわざ統計学の記事を増やす必要もありません。もちろん、世の中のために統計学の記事を増やすことはいいに越したことはないのですが、私たちには限りられた時間しかありません、そこで何に優先順位をつけるかということですね。
さきほどZ検定の時に使ったデータを使います。
そして1標本のt検定を選びます。
ステューデントのt検定
これまでは、母集団の平均値がわかっていて、それに対して手元にあるデータの平均値が有意と呼べるほどに違うのか、つまり手元にあるデータは母集団からサンプルされたと言えるのか、それとも違うのかということが検定したい問題でした。
しかし、実際のビジネスや大学の現場で「一つのサンプルのt検定」が使われることはあまりありません。そもそも母集団の平均値を知っているということがあまりないからです。前節の例では、これまでのデータ全体があたかも母集団かのように扱いましたが、実際は母集団はそこにデータとなっていないものも含めたものです。たまたま私たちのウェブサイトにきた人だけでなく、来てないが来る可能性のあるような人たちも含めた全てが母集団とすべきでしょう。でなければこの分析結果を元に、何か対策をうとうとするわけですが、その対策を打つ対象はこれからのウェブサイトにやってくる人たちで、それは新しい人たち、つまりまだデータとして取れてない人たちなのです。
t検定がよく使われるケースというのは、2つのグループの平均値の差を調べる時です。例えば、先ほどの例であればビジネスユーザーとパーソナルユーザーの2つのグループのそれぞれのサイト滞在時間に違いがあるのかどうか調べたい場合などです。そして今回はこれでいよいよ
ところで、みなさんすでに忘れてしまった人も多いかと思いますが、私たちがほんとうに調べたかったのは手元にある従業員データの会社の男女の平均給料に違いがあるかどうかでした。その場合に使うのはt検定なのですが、独立したサンプルのt検定です。これまで長々と1サンプルのZ検定や1サンプルのt検定を説明してきたのは、いきなり独立したサンプルのt検定に入ると新しいことが多すぎて混乱すると思ったからです。
独立したサンプルのt検定には2つのタイプのものがあります。それはステューデントのt検定、そしてウェルチのt検定です。しかしどちらもこれまで見てきた1サンプルのt検定と考え方は同じです。しかし、差があるかどうかといったときの対象が異なるため、t値の計算の仕方が若干異なります。
まずはステューデントのt検定を見ていきましょう。
ステューデントのt検定
従業員データを見てみると女性の給料は6,700ドル、男性は6,400ドルでした。その差は300ドルです。さて

t検定における帰無仮説
この検定における帰無仮説は2つのグループの間には違いがない、つまり2つのグループの平均値には差がないということになります。
覚えていますか。仮説は反証できる仮説でなければいけません。違いがあるという仮説は反証することができません。今回のように300ドルの差があれば違いがあるじゃないか、で終わってしまいます。そうではなく、だれもが納得のいく数値として定義できる反証の基準が必要となるのです。そこで2つのグループ間には違いがないと定義すると、差がないのですから期待される数値は0です。これは誰もが納得できる数値です。もちろん現実にはデータがばらつくのですから、2つのグループには違いがないにも関わらず、その平均値の差が全く0ということはないでしょう。問題はその差がどれだけ0から遠いのかということになりますが、ここで確率分布を使って確率的に判断することになります。
ところで、2つのグループに違いはないという帰無仮説は、2つのグループは同じ母集団からランダムにサンプルされたと考えることができます。もし同じ母集団から来ているのであれば、その2つのグループ間の平均値の差は0なはずです。もちろんこれは理論的な話であって、実際に現実の世界でどうなるかは別の話です。
というのも同じ母集団からサンプルされたとしても、ランダムにサンプルされている限りはそれぞれのデータは若干違うはずですね。するとそれぞれのグループで平均値を計算するとそれらの値は若干異なるはずです。そしてそうした異なる平均値の差を計算すればおそらく0ではないでしょう。
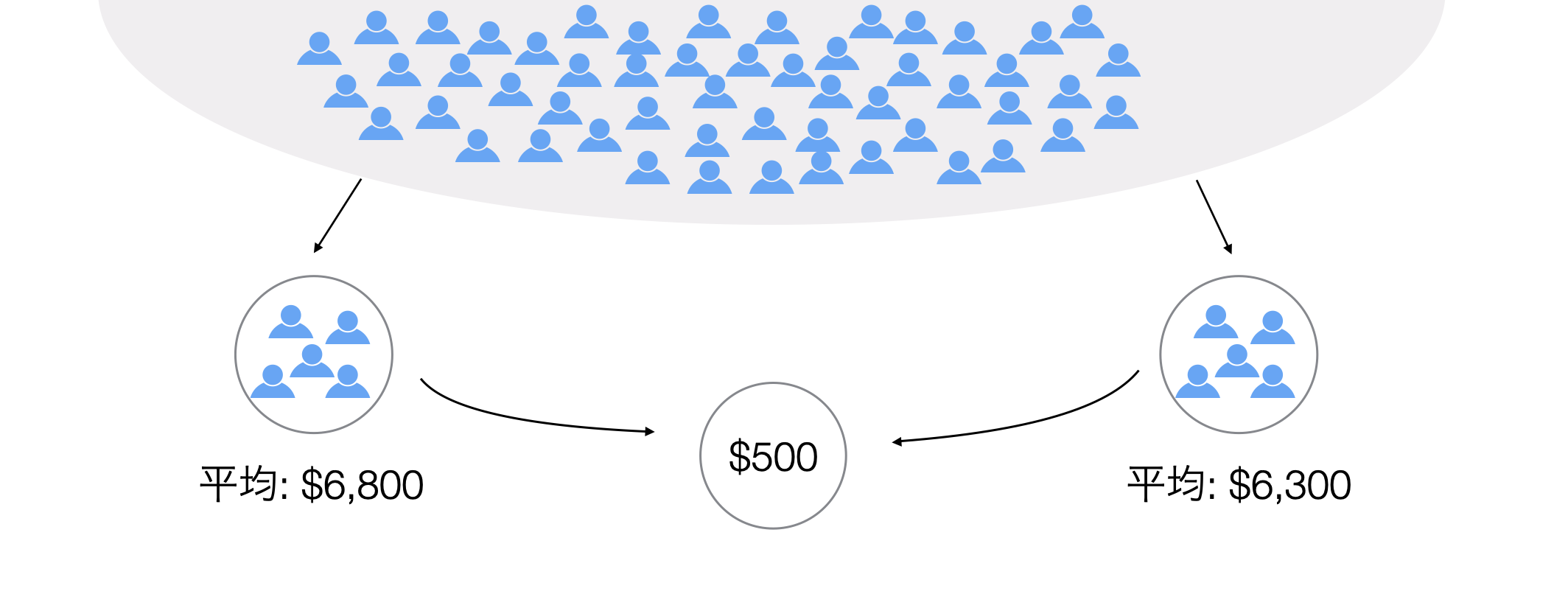
それは絶対的にこういう数値だったら大きいとか小さいと判断できるわけではありません。ここで判断の元となるのはデータのばらつきです。極端なケースでもしデータにばらつきがないのであれば、この300ドルの違いは違いがあると判断するに値するほどの違いと言えるでしょう。というのもこうしてばらつくことのないデータであれば、同じ母集団から何回サンプルしてきたとしてもいつも同じ300ドルの差が出るだろうからです。しかし、現実はデータはばらつきます。5000ドルの給料の人もいれば10000ドルの給料の人もいます。ということはサンプルするごとにサンプルされたグループの平均値は違うでしょう。そしてその違いは300ドルくらいの大きさなのかもしれません。
であれば、同じ集団、つまり男性という母集団があったとして、そこから何回も繰り返しサンプルしたとすると、それぞれのサンプルの平均値の差が300ドルであることもあるかもしれません。
そうであれば、男女間の給料に差があるとなっていた根拠の300ドルは、たとえ同じ男性だとしてもそれくらいの差はあるということですから、これは大したことない、ただのデータのばらつきで説明ができると言えるのです。
今ここで問題になっているのは2つのグループ間の平均値の差がどれだけ大きいのかです。これが帰無仮説である同じ母集団からとったサンプルだとしても多少の差はある、しかしそうした差に比べて、今手元にある2つのグループ間の差はどれだけ大きいのか、どれだけあり得ないほど大きいのかということです。そこでこの差の数値を標準化することになります。これは前の1サンプルのt検定でやったのと同じです。
その計算は以下のようになります。

さてこの標準誤差の計算方法なのですが、これまでとは少し違います。
標準偏差の「プールされた」推定値
ステューデントのt検定では2つのグループの母集団の標準偏差は同じであると仮定します。それではこの標準偏差をどうやって推定すればよいでしょうか。これまでのように対象となるサンプルのデータが1つであれば、そのデータの標準偏差から標準誤差を推定することができました。
しかし今回はデータが2つあります。そこで単純にその2つを平均してやればよいということになります。ただ正確には、重みつき平均値を求めることになります。これを「プールされた標準偏差」として使用します。
まずは重み付き平均の計算の仕方を簡単に攻め値します。
例えば2つのグループがそれぞれ10人だったと考えてみましょう。そしてそれぞれの給料の平均が5000ドル、4000ドルだったとします。その場合、2つの平均の平均は4500ドルとなります。
(5000 + 4000) / 2 = 9000 / 2 = 4500この場合は両方のグループともに同じ人数なので重みづけの心配はありません。両方の平均値に与える重みは1:1となります。しかし、それでも念の為重みをつけたいとしましょう。その場合、それぞれの人数を対応する平均値に掛けて上げれば良いのです。
5000 * 10 + 4000 * 10 / 2 = 45000しかしこれではもはや全体の平均値ではなく、むしろ全体の合計値に近い値になってしまいます。そこで分母の方も同じように全体の人数を掛けることで、平均値となります。
(5000 * 10 + 4000 * 10) / (10 + 10) = 4500ようは分子にも分母にも10をかけているわけですから、答えは元の10をかけていなかった場合と同じとなります。なんかめんどくさいことをしているように見えるかもしれませんが、これが重みづけ平均の計算の仕方です。さて重みづけ平均が意味をなしてくるのはここからです。
もし片方のグループは8人でもう片方は2人だったらどうでしょう。それぞれの平均値を足して2で割るのは、この人数差を考慮していない分それは全体の平均を表しているようには見えません。そこでこの人数差を計算式に加味するために先ほどの重みづけ平均の計算式を使うと、その平均は4800となります。
(5000 * 8 + 4000 * 2) / (8 + 2) = 4800これは5000と4000の中間である4500に比べて5000の方によった数値となっています。それもそのはずで、なぜなら5000という平均値の方にはより人数が多かったからです。
さて、これをここでの標準偏差の重みづけ平均に応用してみましょう。
まずは標準偏差は分散をルート(平方根)したものですね。
標準偏差 = sqrt(分散)ルートした値を重みづけ平均するのはややこしくなるため、元の分散のほうの値を重み付け平均し、その後にルートすることで標準偏差に戻してみたいと思います。
分散の平均 = (分散A + 分散B) / 2これに重み付けをします。
分散の重みづけ平均 = (分散A * N1 + 分散B * N2) /(N1 + N2)こうして求まった分散の重みづけ平均値にルートすれば標準偏差の重み付け平均が算出できます。
標準偏差の重みづけ平均 = sqrt((分散A * N1 + 分散B * N2) /(N1 + N2))さてここで1つ言い忘れていたことがあります。それはこの重み付け平均の計算をする際にバイアスの補正、つまり自由度のことを考慮していませんでした。ここでの標準偏差は正確には母集団の推定された標準偏差です。その場合はNではなく、N-1というバイアスの補正をかける必要があります。すると上記の式でNに関するもの全てに−1を加えます。
標準偏差の重みづけ平均 = sqrt((分散A * N1-1 + 分散B * N2-1) /(N1-1 + N2 -1))
標準偏差の重みづけ平均 = sqrt((分散A * N1-1 + 分散B * N2-1) /(N1 + N2 -2))式はややこしくなりましたが、やろうとしていることは同じです、2つのグループの推定された標準偏差の重み付け平均をしたということです。
さて、この標準偏差が求まったら、この標準偏差の推定値を元に標準誤差を計算したいのですが、
標準誤差 = 標準偏差 * 1/sqrt(N)としたいところですが、そして、先ほど計算した標準偏差に、1/sqrt(N)を掛け合わせたいのですが、今回は2つのグループがあるのでN1とN2があります。
そこでsqrt(N)の部分が
標準誤差 = 標準偏差 * sqrt(1/N1 + 1/N2)となります。
ところでここで出てくる標準誤差とは何の標準誤差なのでしょうか。1サンプルのt検定のときは手元のデータの平均に関心があり、その値が母集団の平均、つまり真の平均に比べて有意なほど大きいのかどうかを判断したかったのです。そこでその大きさを標準化した数値として標準誤差で割って上げたのでした。つまりここでの標準誤差は平均値の標準誤差ということになります。平均値がどれだけばらつくかの指標ということですね。
そして、手元のデータを元に推定値である標準偏差を計算し、それに1/sqrt(N)を掛け合わせたることで標準誤差を計算し、その標準誤差をもとに手元の平均と母集団の平均の差がどれだけ大きいのかを表す指標としてt値を計算しました。
今回のステューデントのt検定では2つのサンプルがあり2つの平均値があります。そして私たちはその差に関心があり、その差が有意と呼べるほど大きいかどうかを判断したいのです。そこでこの差のを標準化するために標準誤差で割りたいのです。つまりここでの標準誤差とは差の標準誤差のことであり、差がどれだけばらつくかの指標と考えることができます。
さて、ここで標準誤差が求まったのであとは、2つの平均値の差を標準誤差で割ることで標準化し、t値を計算します。
t = mean(A) - mean(B) / 標準誤差これがステューデントのt検定におけるt値の計算方法です。
そしてもし同じ母集団から何度も2つのサンプルを抽出しこのt値を計算するということをなん度も繰り返したのであれば、上記の式を使って算出されたt値の分布は、当たり前かもしれませんが、0を中心とした左右対称なt分布となります。

このt分布は以前見たように自由度によって多少形が変わってきます。その自由度は今度はデータが2つあるために以下のようになります。
自由度 = N1-1 + N2-1 = N - 2ここではN1とN2を足した全体の数をNとしています。繰り返しますが、t分布はデータの量が増えると正規分布になります。正確には上記の自由度が大きくなると正規分布になるということなのですが、データの量が増えると自由度が大きくなるため、正規分布に近づく、または正規分布になるということです。

そして、t値とt分布がわかれば、あとはいつもの仮説検定の手続きを行うだけです。つまり、t分布を元に、もし2つのグループに違いがないとしたときでも手元のデータから算出されたt値かそれ以上に大きい値が起きうる確率はどれくらいなのかということを計算できるようになります。そしてこの確率がt検定におけるP値となります。
それが有意水準よりも低ければ有意、高ければ有意でないと判断し、有意であれば帰無仮説を棄却できるので2つのグループには差があるという結論となり、逆に有意でなければ帰無仮説を受け入れ続ける、つまり差はないと結論づけることになります。
もしt値が1だとすると、その場合のP値はデータ量がある程度あったとすると32%となります。つまり帰無仮説が正しいとすると得られた1かそれ以上に大きい、または−1かそれ以下にに小さい値が得られる可能性は32%ということであり、
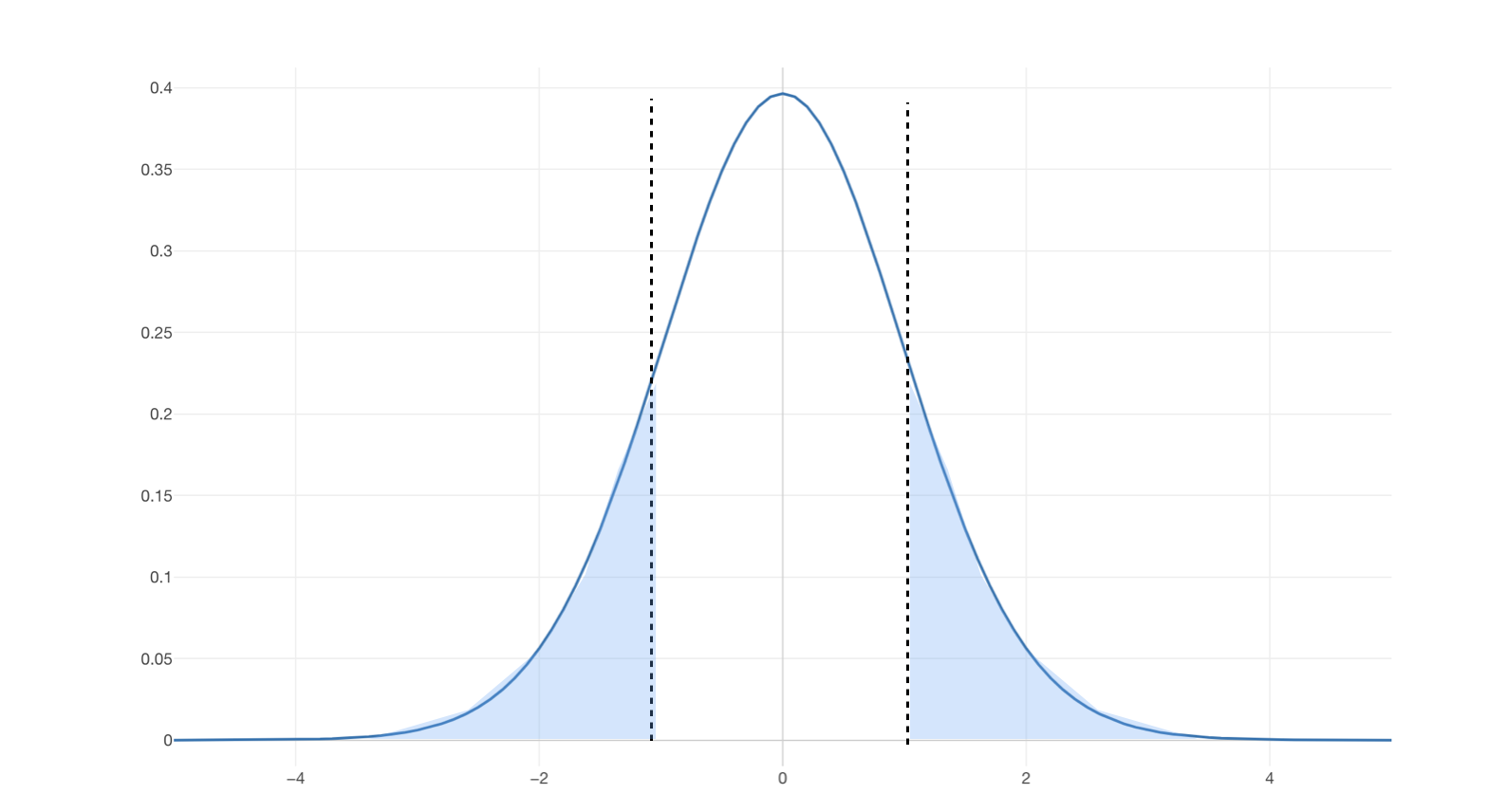
有意水準が5%であれば、それよりも大きな値なため有意ではないと判断できます。つまりそれくらいであれば2つのグループに違いがない、つまり同じ母集団から出てきてるグループだとしても、それくらいの差であればサンプル誤差と言える範囲ですよということです。
片側検定と両側検定
ところで、t値はいつもプラスの値というわけではありません。マイナスの場合もあります。
Let’s do it!
ウェルチのt検定
この章の最初に最終的に行き着きたいのはウェルチのt検定だという話をしたのを覚えていますか。ようやくそこにやってきました。さて、そもそも私たちが調べたかったのは男女間の給料に差があるかどうかということでした。そしてその答えをステューデントのt検定で出したのですが、実は1つ問題があります。
というのはステューデントのt検定にはいくつかの前提があるのですがそのうちの1つを満たしていないのです。それは等分散というやつです。これは2つのグループの母集団のばらつきの幅、つまり標準偏差が同じであるというものです。これを見極めるための検定手法というものもありますが、それはANOVA検定の際に紹介します。
今回のデータは2つのグループの標準偏差はほぼ等しいため特に問題がありません。
しかしこれら2つのグループの標準偏差が同じでないことはよくある話です。
そもそも2つの標本の平均値が同じでないとしたら,そこでなぜ同じ標準偏差を持っていることが仮定できるのでしょうか。
そういった場合を考慮したものがウェルチのt検定というものです。
これらを考慮した上でグループ間の差を標準化するためには以下のような式を使うことができます。

この場合の分母は見たところややこしそうですが、これは三角関数という手段を使ってAの標準誤差とBの標準誤差の平均を計算しようとしています。
<image>
感覚的には2つの標準偏差の平均と考えてもらって差し障りありません。
さて、ここでのウェルチのt検定における自由度を求める数式は
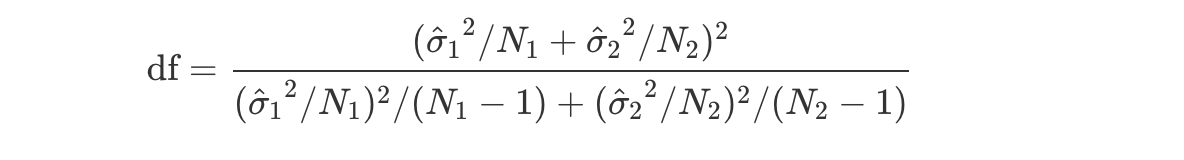
これを日本語にすると以下のようになるのですが、これでもわけわかりませんね。
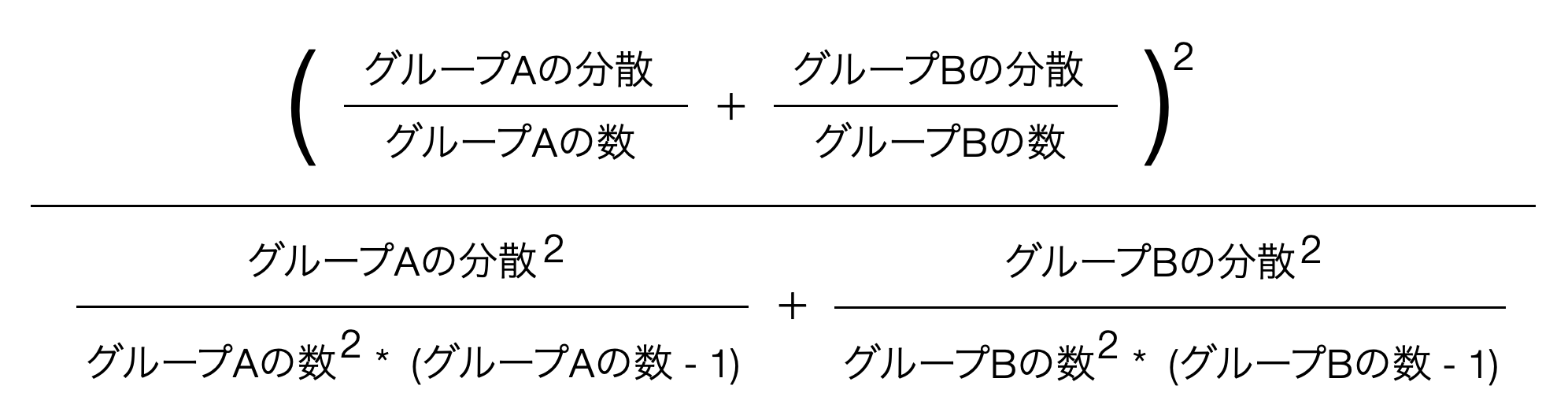
これらの数式の説明はこの本がカバーする範囲を超えますので、これ以上は踏み込みません。またこれらの数式を覚える必要も、数式のロジックを理解する必要もありません。しかし、重要なポイントとしてはウェルチの検定では「自由度(df)」の値がスチューデントの検定より少し小さくなる傾向にあり,そして必ずしも整数にはならないということです。
前提条件
ウェルチのtt検定の仮定はスチューデントのt検定のものと非常によく似ています。ただし,ウェルチの検定では分散の等質性についての仮定がありません。そのため,仮定されているのは正規性と独立性だけということになります。これらの仮定の具体的な内容は,ウェルチの検定とスチューデントの検定で同じです。
Let’s do it!

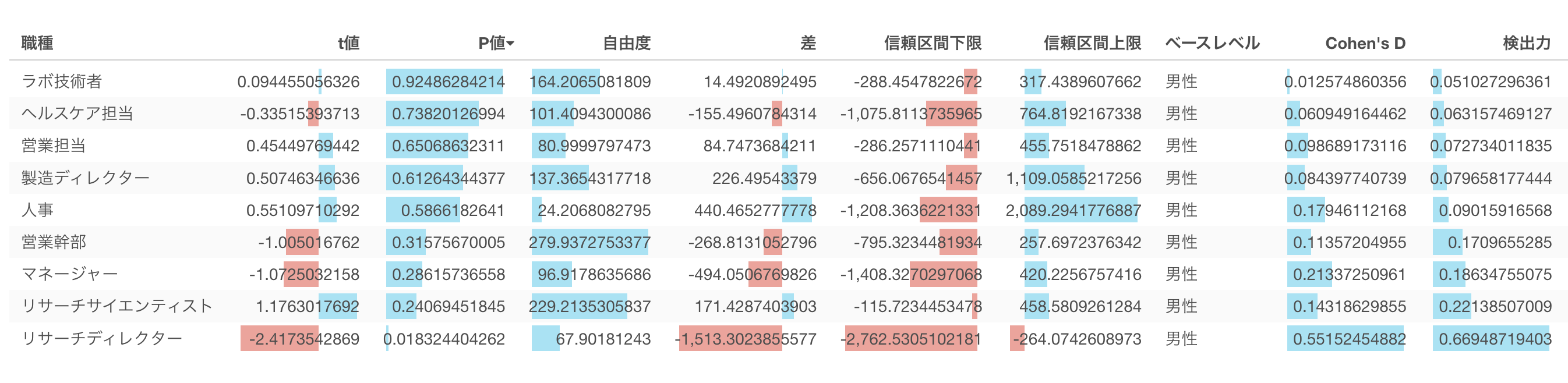
職種ごとに見てみる
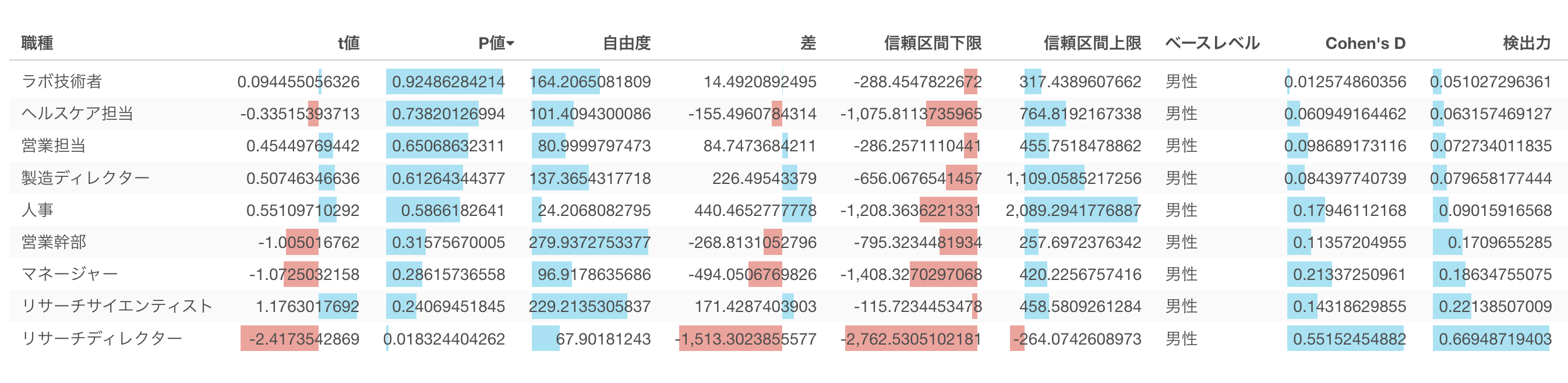
効果量
今回の検定では全体では男女間の給料の違いは有意ではありませんでした。しかし職種ごとに見てみるとリサーチディレクターの場合のみ有意という結果になりました。
さて、この有意だった際に一つ考慮すべきことがあります。それは中心極限定理です。中心極限定理によればデータの量が増えればばらつきは小さくなるという話をしました。ということは、同じ300ドルの差だとしても、データ量が増えればそのばらつきが変わらない限りは有意となりやすい傾向があります。
t値の詳細を省いた概念的な計算式は以下となります。
t = mean(A) - mean(B) / 標準誤差データの量が増えれば増えるほど、この標準誤差が小さくなるわけですから、t値の値は大きくなります。
そしてt値が大きくなればなるほどP値は小さくなるためそのぶん有意となりやすくなります。
<image>
逆に、差が1000ドルだとすると値としてはそれなりに大きいにも関わらず、データが少ないせいで標準誤差が大きくなり、その分t値が小さくなり、その分P値は大きくなるため有意とならないこともあり得ます。
つまり、統計的に有意ではあるが、そこで問題になっている差は大したことなかったり、また逆に、統計的に有意とはならかったが差はそれなりに大きかったりする場合があるということです。つまり、その根拠となるP値をもってしても、有意かどうかという結論だけではそれをもって違いがあるないの判断をするには物足りないということです。
そこでこの検定を行った際に問題となっている対象、t検定の場合であれば2つの平均値の差がどれだけの大きさであるのかを示す指標として効果量というものが使われます。検定の結果を報告する際に、P値だけでなく、この効果量もいっしょに提示することで、意思決定するさいに、有意だという結論を補足する情報として役立ちます。
この効果量はそれぞれの検定手法によって異なる指標があるのですが、t検定においてはもっとも一般的に使用されている効果量の指標はコーエンのd(Cohen’s d)と言われるものです。
これは基本は非常にシンプルな指標です。手元のデータの標準偏差で標準化したものです。t値を求める際には、標準誤差を使って標準化しましたが、ここではそのまま手元のデータの標準偏差を使います。そこで基本的には以下のような式で求めることができます。
差 / 標準偏差この章ではいくつかのタイプのt検定の手法を見てきました。ここでもそれぞれの手法についての効果量を見ていきたいと思います。
1サンプルのt検定
まずは1サンプルのt検定の効果量です。
t値を求める式は
(手元のデータの平均値 - 母集団の平均値) / 標準誤差効果量の場合は標準誤差の代わりに標準偏差となります。
(手元のデータの平均値 - 母集団の平均値) / 標準偏差ステューデントのt検定
ステューデントのt検定におけるt値の計算式は以下となります。
t = mean(A) - mean(B) / 標準誤差そしてこの場合も標準誤差の代わりに標準偏差で割ることで標準化します。
ただここで思い出して欲しいのですが、ここでの標準偏差の計算は気をつけなければいけません。というのも2つのグループがあるため2つの標準偏差があります。単純にそれら2つの標準偏差の平均を取りたいところですが、それぞれのデータ量(行数)が違うため重み付け平均をとらなくてはいけません。そこで以下のような式になります。
標準偏差の重みづけ平均 = sqrt((分散A * N1-1 + 分散B * N2-1) /(N1 + N2 -2))標準偏差が求まればそれで割ることで効果量が算出できます。
効果量 = mean(A) - mean(B) / 標準偏差の重みづけ平均ウェルチのt検定
ウェルチのt検定の場合は2つのグループのばらつきが同じであると仮定できないため、2つの推定された標準偏差の重みづけ平均をとるのではなく、単純に2で割るという形の平均を取ります。そのさいにルートして標準偏差にする前の分散の平均を取り、その平均値をルートして標準偏差とします。
効果量 = mean(A) - mean(B) / sqrt((分散A + 分散B) / 2)さてこのようにして求まった効果量dですが、これにはいちおう以下のようなガイドラインがあります。
| Cohen’s d | 効果の大きさ |
|---|---|
| 0.2 | 小さい |
| 0.5 | 中程度 |
| 0.8 | 大きい |
いちおうと言ったのは、これは絶対視するものではなく、あくまでもガイドラインとして参考にしてくださいというべきものです。
p値が有意でも、効果量が小さいとその差は「統計的には有意だが、実際にはほとんど意味がない」可能性があるということです。
そして「差が統計的に有意かどうか」と「その差が実質的に意味があるかどうか」は違う話だということです。もちろん基本的には相関しているものではあります。ただ、データ量によってそうとも言えないことがあるということです。
統計的有意性に使うp値は差がただのデータのばらつきの範囲なのかどうかを判断するものであって、小さいほど有意となりやすいものです。 効果量は差が「どれくらい大きいか(実際に意味があるか)」を示すものであって大きいほどより意味のある違いだと言えます。そして、P値はデータ量によって変わってくるのに対して、効果量はデータ量にに左右されにくいという特徴があります。