3つ以上の平均値の比較
女子学生:2つのグループ間の平均の違いについて調べるときはt検定が使えますが、グループの数が3つ以上の場合はどうするんですか?
男子学生:その場合はANOVA検定を使えばいいんですよね。
女子学生:ANOVAってどういう意味なんですか。
先生:ANOVAはAnalysis Of Varianceの略で、日本語ではANOVA検定、または分散分析と呼ばれます。
女子学生:分散に関する分析ということですか。
先生:平均値の違いに関する分析なんだけど、分散、つまりデータのばらつきを元に分析するからそういう名前がついています。この章では、ANOVA検定と呼ばれる検定手法について見ていきたいと思います。
ANOVAの基礎
ANOVA検定と言っても実はいくつかのタイプのものがあります。まず、一般的で最もよく使われるものがOne-way ANOVA(一元配置分散分析)と呼ばれるものですが、これは1つの説明変数に含まれる複数のグループによる平均値の違いが十分に大きいと言えるのかを分析するときに使われるものです。例えば3つの学校による平均点の違いを調べるときなどです。
これに対して2つの説明変数による平均値の違いを分析するのがTwo-way ANOVA(二元配置分散分析)と言われるものです。例えば3つの学校による平均点の違いについて調べたいのですが、それぞれの学校では男女の割合が若干違います。その場合学校による違いなのか男女による違いなのかがよくわかりません。そこでこうした2つの変数による影響を同時に調べるための手法がTwo-way ANOVAです。
さらにANOVA検定には他にもいくつかのタイプがあるのですが、この本ではその中でも一般的によく使われるOne-way ANOVA(一元配置分散分析)を紹介します。この章ではこのタイプの検定を単純にANOVA検定と呼びます。
学校のテスト結果の分析
これから学校のテスト結果という例を使ってANOVA検定の解説をしていきたいと思います。
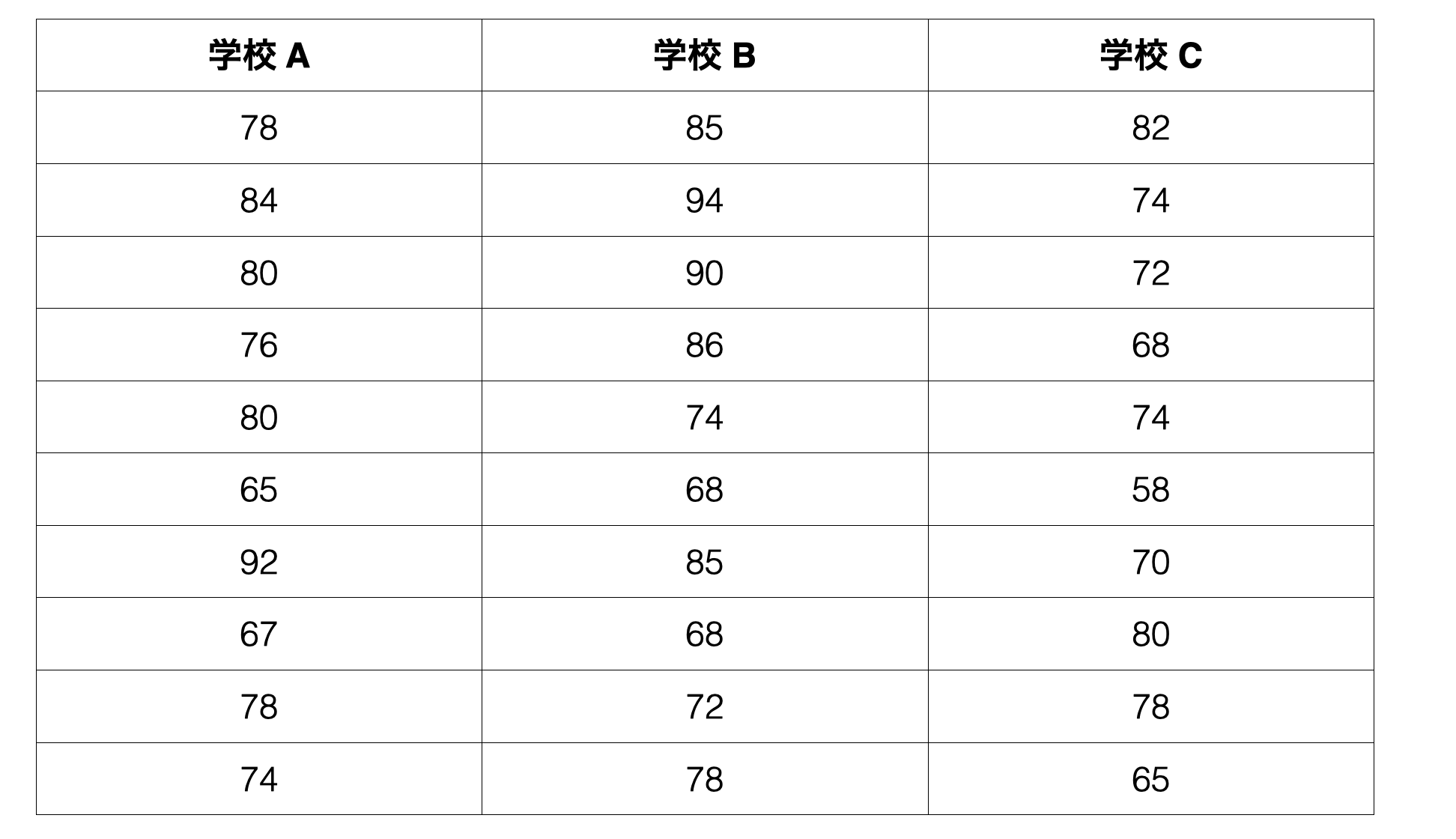
ある学区には3つの学校があります。これらの学校では生徒の数学の成績に違いがあるのかどうか調べようとしていたとしましょう。以下がそれぞれの学校での数学の生徒ごとのテスト結果です。
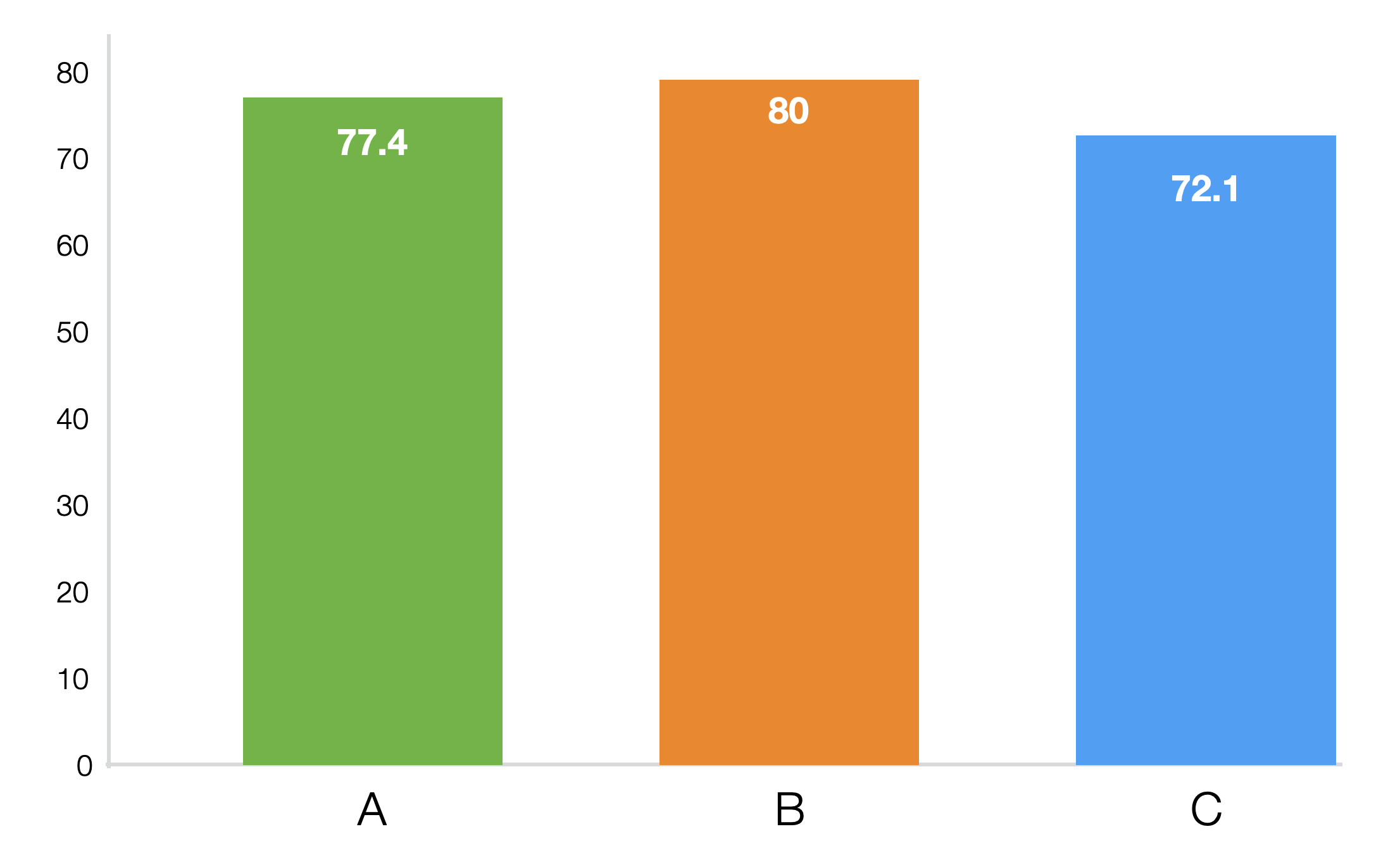
それぞれの学校の平均スコアをチャートにしたのが以下のものです。
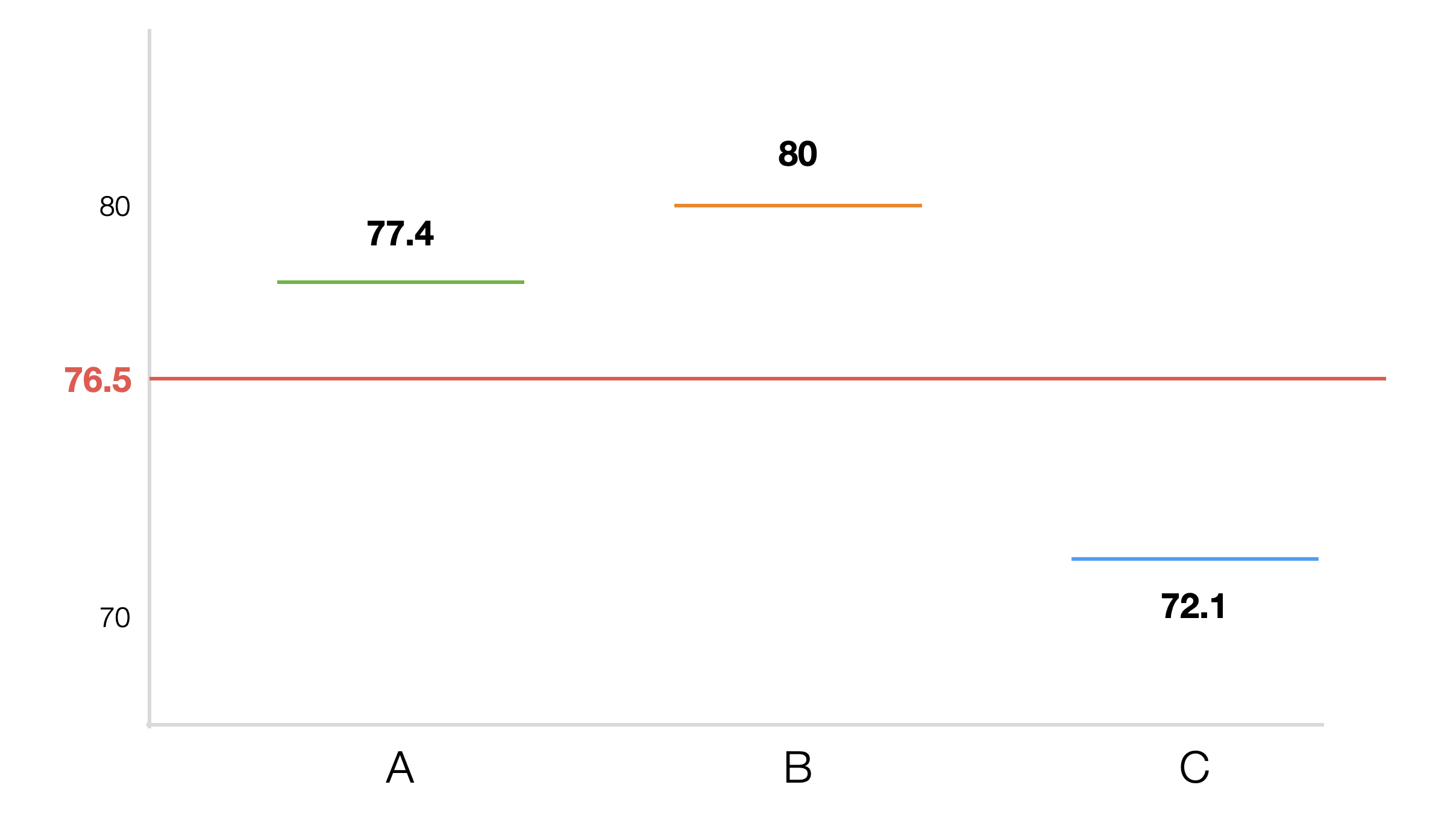
平均点を比べると学校Bが最も高く、その後にA、そしてCという順位になっています。さて、これらの差はほんとうに違うと言えるほどのものなのでしょうか、それともただのデータのばらつきによる差なのでしょうか。もしグループの数が2つであれば、前節で学んだt検定が使えますが、今回はグループの数が3つなので使えません。そこで3つ以上でも使えるANOVA検定を使うことになります。
帰無仮説
ANOVA検定における帰無仮説は、複数のグループ間の平均値には差がないというものです。学校の例では3つの学校の平均点の間には差がない、つまり平均点が同じであるということです。
それではもし検定の結果帰無仮説を棄却できたとすると、それはいったい何を意味するのでしょうか。もちろん、「差がない」の反対は「差がある」ということなのですが、ANOVA検定においてはグループが3つ以上あります。そこで差があるというのは何の差があるのかはっきりしません。しかし、実は単純です。複数のグループのうち少なくとも1つの平均値は他と有意な差があるというものです。学校の例であれば、3つの学校のうち少なくとも1つの学校の平均点は他の学校と有意な差があるということになります。
ばらつきの分析
さて、帰無仮説が「差がない」だとしても、データはばらつくわけですから、若干は違いがあるでしょう。そこでそれら複数のグループの平均値の差は、同じ母集団からランダムに取り出した複数のグループ間の差と同程度なのか、それともそういった同じ集団からからでてきたという前提では説明しきれないほど大きい差なのかが問題となります。
そこで複数のグループ間の平均の差の大きさを統計値として表す必要があります。t検定の時は、2つのグループ間の平均値の差を標準化したt値を統計値として算出し、このt値の大きさを元に差が有意かどうかの判断をしました。
ANOVA検定の場合はグループが複数あるため単純に差と言っても全ての組み合わせの数だけ複数の差があります。学校の例であれば、AとB、BとC、AとCといった具合にです。そこで差の代わりに複数の平均値のばらつきの大きさを使います。
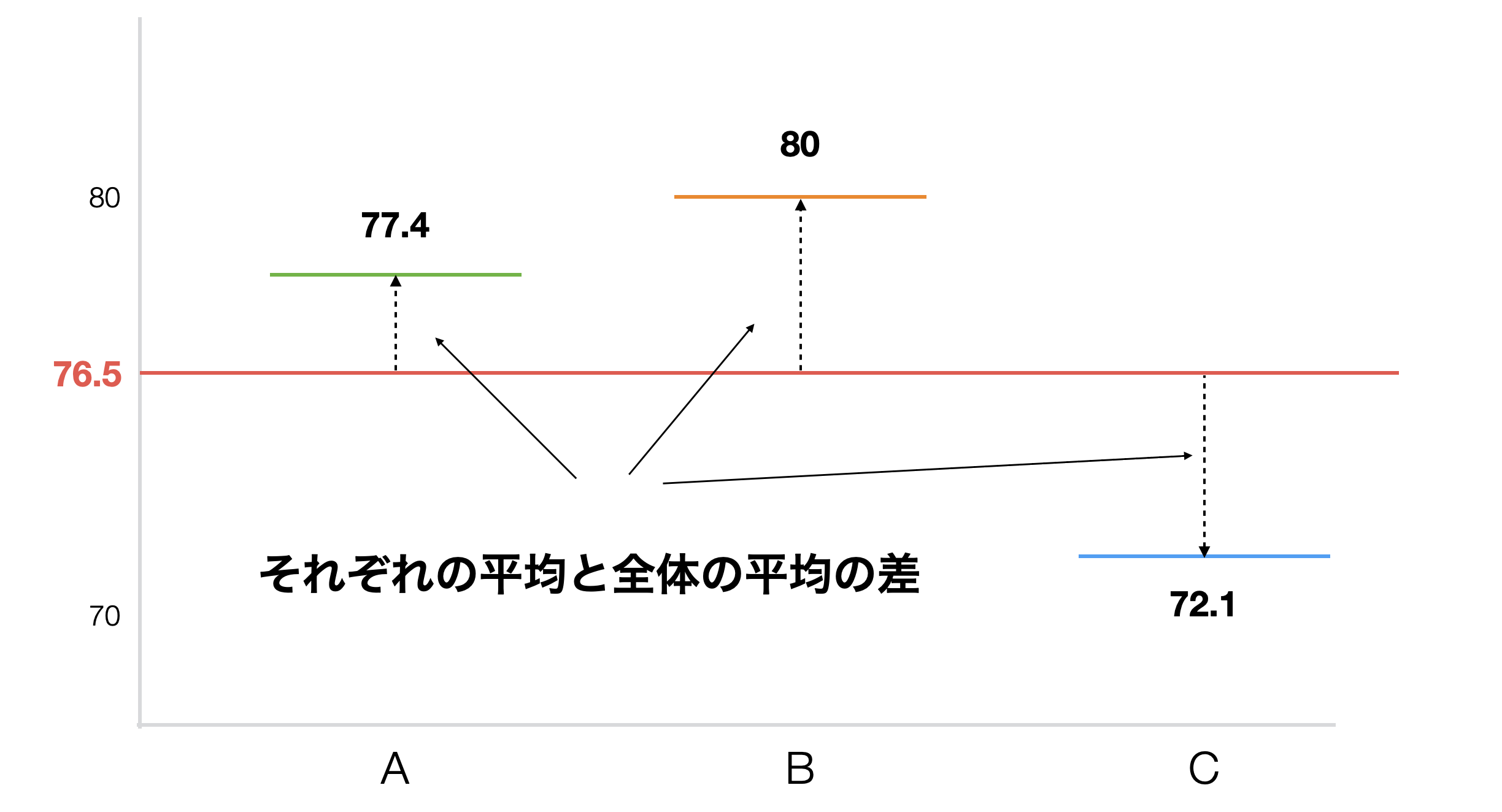
実はこれこそがANOVA検定が分散分析、つまりばらつきの分析と呼ばれる所以です。ANOVA分析では、データ全体のばらつきをグループ間の平均のばらつきとグループ内のばらつきに分けることができると考えます。
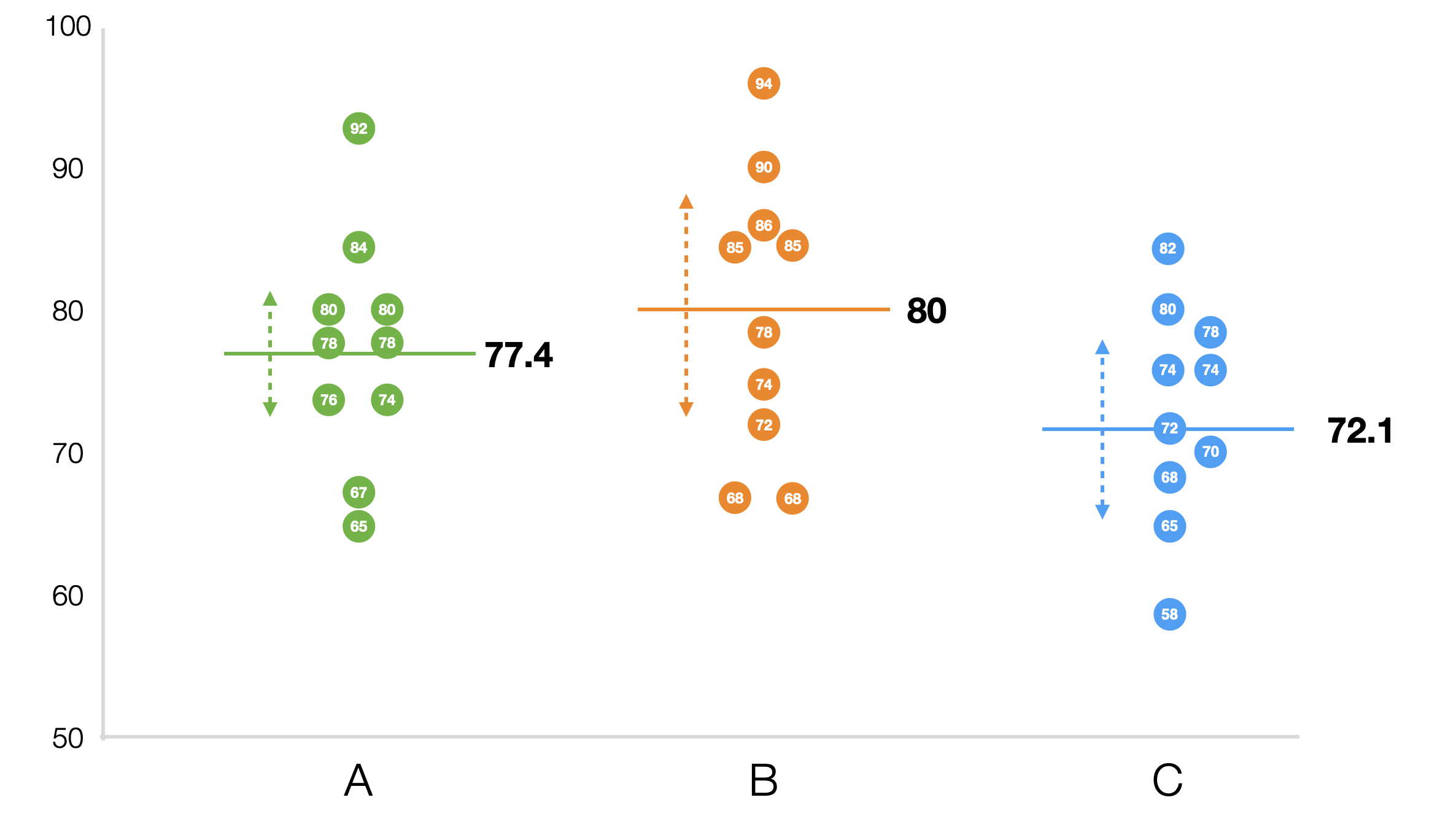
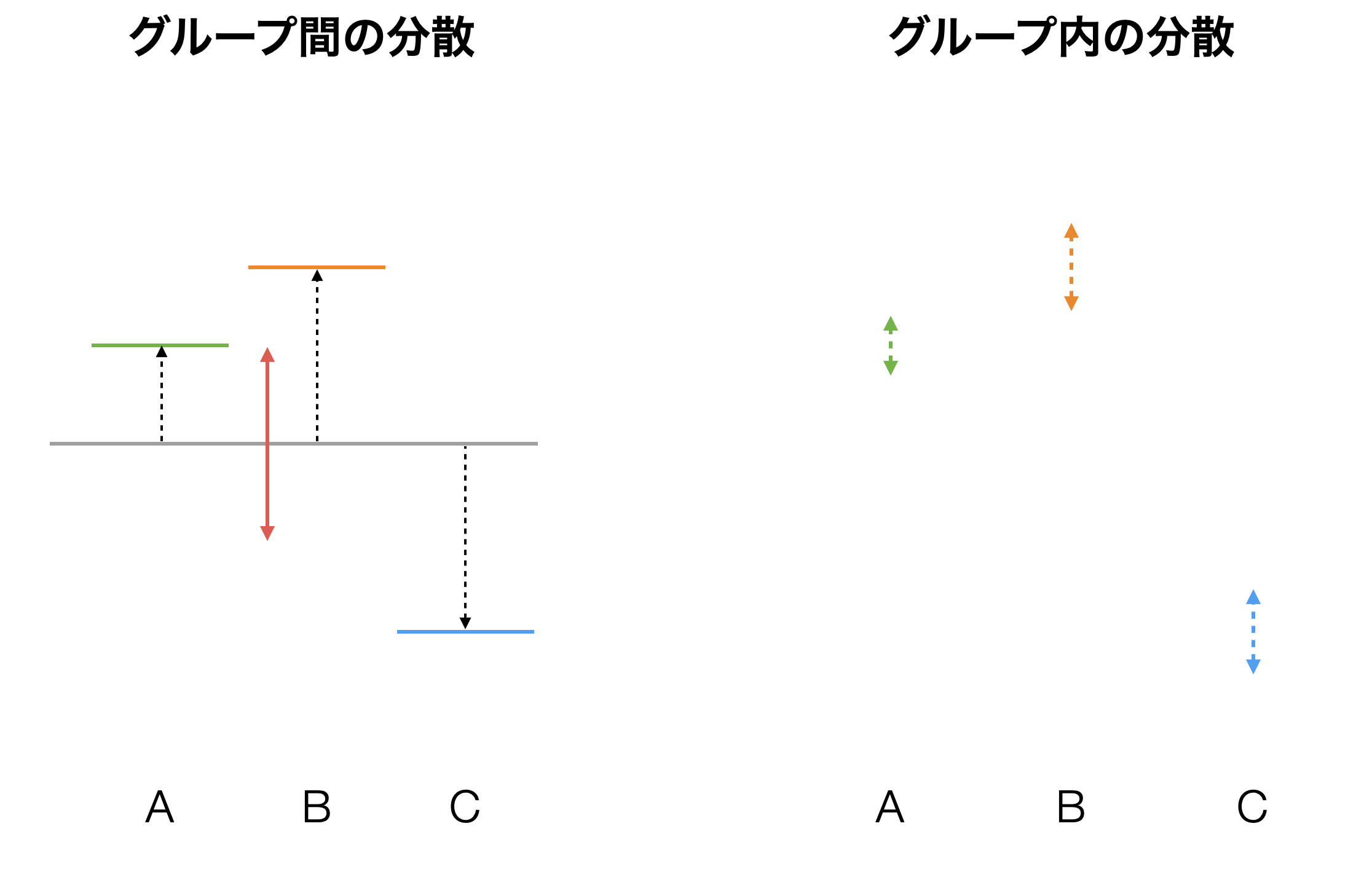
例えば学校の平均点といったデータがあった場合、全生徒の平均点はばらついています。このデータを学校というグループによって分けると、全体のばらつきは2つのタイプのばらつきに分けられます。1つは学校間の平均値のばらつきで、もう1つはそれぞれ分けられた学校内でのそれぞれの生徒の平均点のばらつきです。この学校間の平均点のばらつきとは学校の違いによってできたもののはずです。もし学校間に違いがないのであれば、学校間の平均点のばらつきは小さいでしょう。逆に、学校間に違いがあるのであれば、学校間の平均点のばらつきは大きいでしょう。
ところで、このグループ間の平均値のばらつきが大きいのか小さいのか、もう少し正確に言うとそれは統計的に有意と言えるほど大きいのか、それともただのデータのばらつきと言えるほど小さいものなのか、どう判断すれば良いのでしょうか。
そこで、このばらつきの大きさの比較対象となるのが、このグループ以外の要因によってできたもの、すなわちグループ内のばらつきです。
学校の例で言えば、それぞれの学校の生徒の点数にはばらつきがあります。
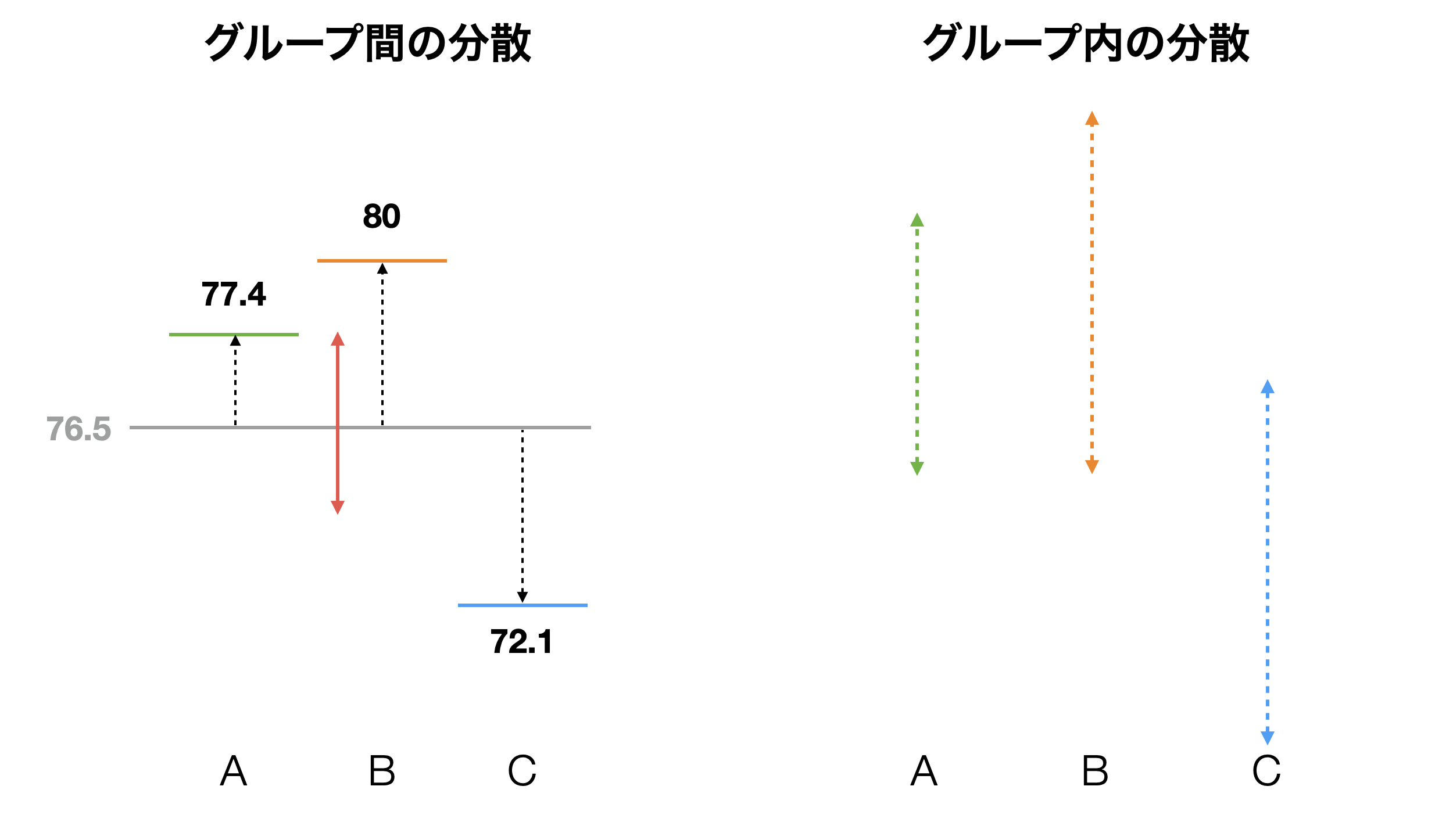
こうしたばらつきは学校の違いという要因では説明できません。他に何か別の要因があるのでしょう。例えば、家庭環境、勉強の習慣、ダイエット、またはただの偶然、などといった具合にです。
そして、この学校という要因で説明できるばらつきが、それ以外の要因によるばらつきと比べてどれだけ大きいのかをF値という統計値によって計算し、この値を元に、学校の違いによるテストの平均点の違いが有意なのかどうかを判断しようとする手法がANOVA検定です。
F値と呼ばれるグループ間の平均値のばらつきとグループ内のばらつきの比率を算出するための式は概念的に以下のようになります。
\[\begin{aligned} F値 = \frac{グループ間の平均値のばらつき}{グループ内のばらつき} \end{aligned}\]F値の計算
ここから、F値を計算するにはグループ間の平均値のばらつきとグループ内のばらつきを算出する必要があります。それぞれ順を追って詳しくみていってみましょう。
グループ間の平均のばらつき
グループ間の平均値のばらつきとは、正確には「グループ間の平均値のばらつきの2乗平均」のことです。これはそれぞれの平均値と全体の平均値との差を求め、それらを2乗したものを足し上げ、その後平均をとります。この平均を取る前の2乗したものを足し上げた数値を「グループ間の平均値のばらつきの2乗和」と呼びます。
ここでは、まずこの「2乗和」の計算を見ていきたいと思います。
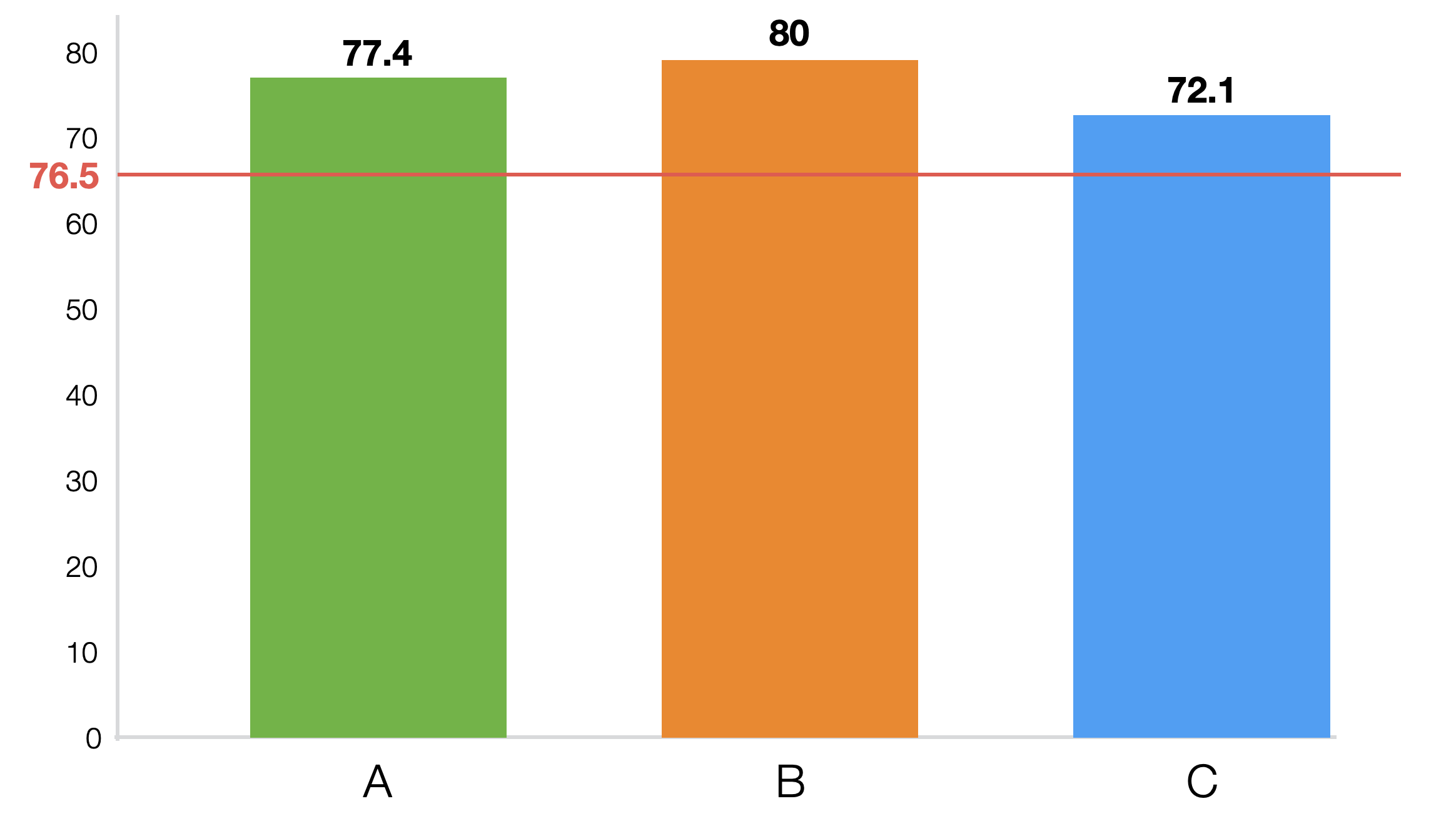
学校の例では、全体の平均値は76.5なので、まずそれぞれの学校の平均値との差を計算します。この値を偏差と呼びます。
| 学校 | 平均スコア | 偏差 |
|---|---|---|
| A | 77.4 | 0.9 |
| B | 80 | 3.5 |
| C | 72.1 | -4.4 |
分散の計算の時にも見たように、これらの偏差の値を足し上げると0になりますから、ここでもそれぞれの偏差を2乗します。
| 学校 | 平均スコア | 偏差 | 偏差の2乗 |
|---|---|---|---|
| A | 77.4 | 0.9 | 0.81 |
| B | 80 | 3.5 | 12.25 |
| C | 72.1 | -4.4 | 19.36 |
これらを2乗したものを足し上げることで、学校という要因によるばらつきの大きさを計算したいところなのですが、これでは全体のばらつきを「グループ間の平均のばらつき」と「グループ内のばらつき」の2つに分けたことにはなりません。

というのは全体のばらつきとは全員、つまり全生徒の点数のばらつきだからです。そこでそれぞれの学校の生徒の数である10をさきほどの偏差の2乗に掛ける必要があります。
| 学校 | 平均スコア | 偏差 | 偏差の2乗 | 偏差の2乗 x 人数 |
|---|---|---|---|---|
| A | 77.4 | 0.9 | 0.81 | 8.1 |
| B | 80 | 3.5 | 12.25 | 122.5 |
| C | 72.1 | -4.4 | 19.36 | 193.6 |
こうしてデータ量(生徒数)を掛けるというのは、それぞれのグループ間での人数の違いを考慮するという点からも重要です。今回はたまたまそれぞれのグループの人数が同じですが、もし5人しかいないグループと100人いるグループがあった場合、それぞれの平均値をそのまま足し上げてしまうと、100人いるグループの重みを無視してしまうことになります。
そこで、偏差の2乗にグループの人数を掛け合わせてから、足し上げることで、グループの違いが与える影響をより正確に測ることができるのです。
そしてこれらすべての重み付け偏差2乗を足し上げたものが「グループ間の平均値のばらつきの2乗和」となります。
\[\begin{aligned} 8.1 + 122.5 + 193.6 = 324.2 \end{aligned}\]ここまでやってきたことを数式にすると以下のようになります。
\[\begin{aligned} グループ間のばらつき = Aの数 \times (Aの平均 - 全体の平均)^2 + Bの数 \times (Bの平均 - 全体の平均)^2 + Cの数 \times (Cの平均 - 全体の平均)^2 \end{aligned}\]それでは次にグループ内のばらつきの大きさについて見ていきましょう。
グループ内のばらつきの大きさ
以下のチャートはぞれぞれの学校のそれぞれの生徒の点数を丸で表しています。
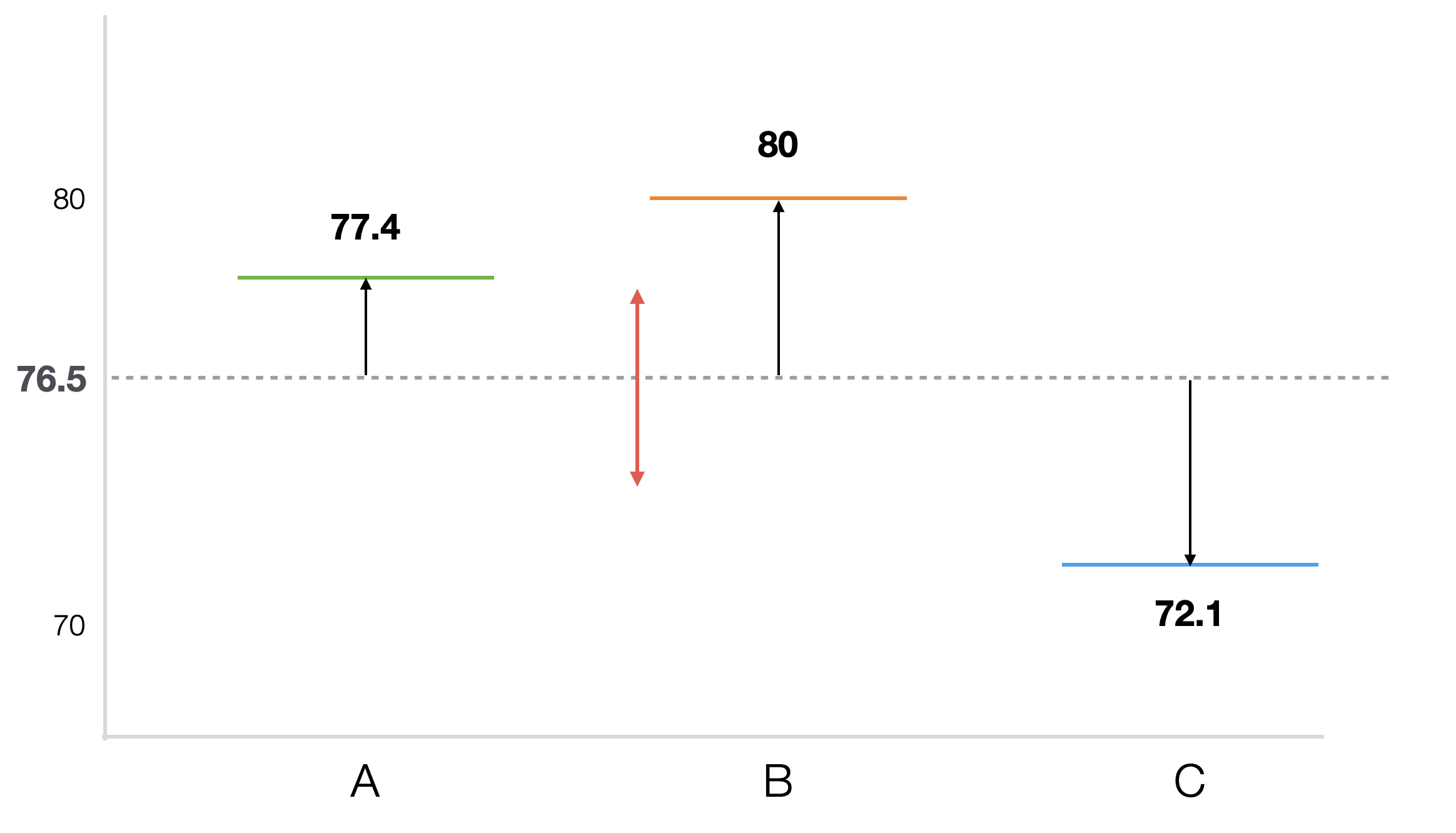
見ての通りそれぞれの学校の生徒の点数にばらつきがありますが、このグループ内のばらつきの大きさをこれから計算したいと思います。
まず、それぞれの生徒とそれぞれの生徒が属する学校の平均との差である偏差を計算します。
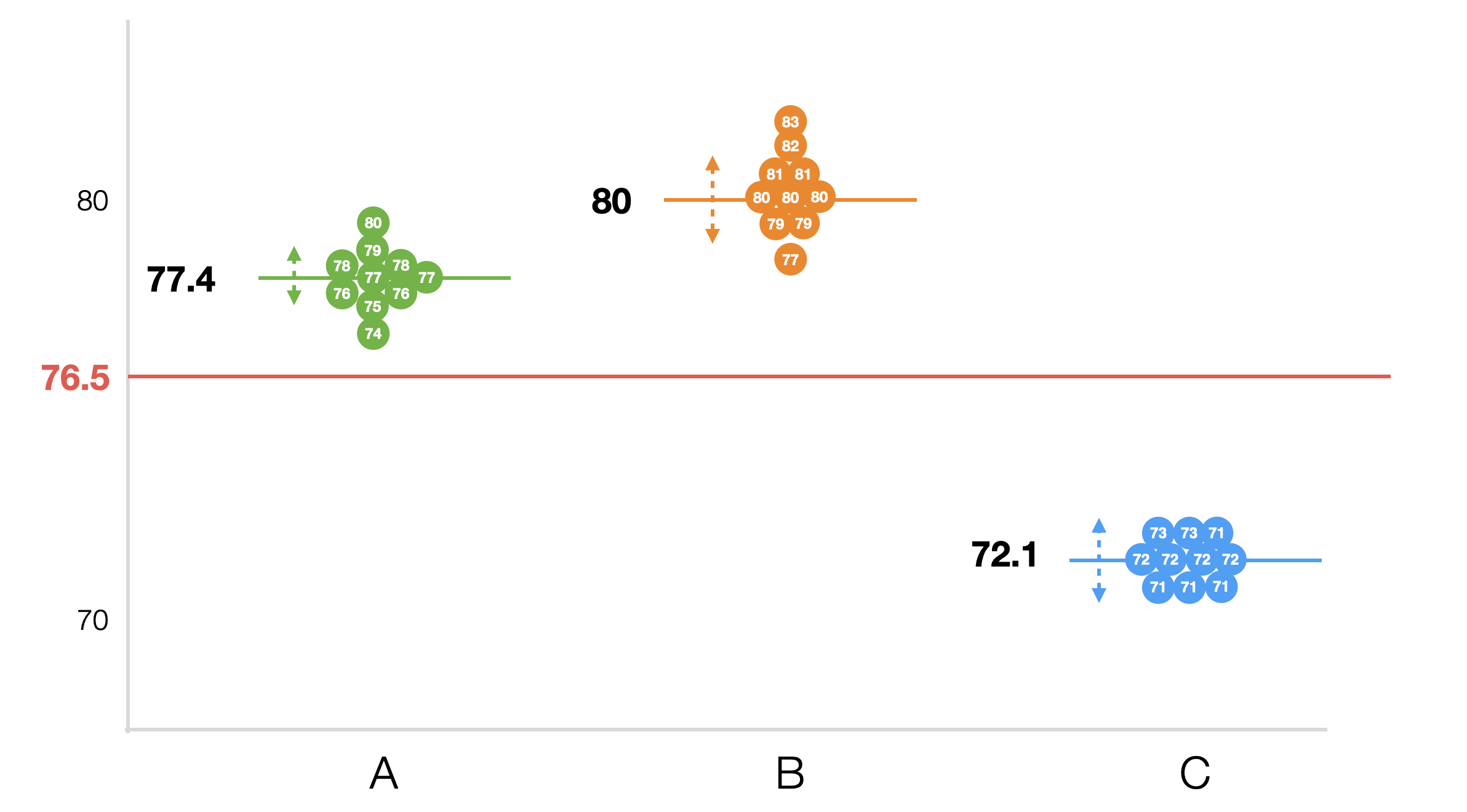
そしてこれらを2乗したものをそれぞれの学校毎に足し上げます。
これらを全て足し上げると、1793.3となります。これがグループ内のばらつきで、「グループ内2乗和」と呼ばれるものです。
全体のばらつきの大きさ
ところで、さきほどのグループ間の平均のばらつきの大きさとグループ内のばらつきの大きさを足し上げると全体のばらつきの大きさになるはずです。

全体のばらつきとはそれぞれの値が全体の平均からどれだけばらついているかのことです。
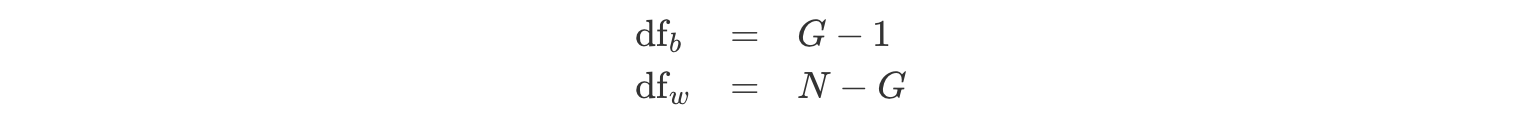
これはいわゆる分散と同じものです。ただ、ここでは人数分で割って平均を計算するのではなく、その手前のそれぞれの値と全体の平均との差の2乗を足し上げた値を「全体のばらつきの和」として使います。
そこで、まず全体の平均値である76.5との差である偏差を計算し、それぞれを2乗(偏差の2乗)します。
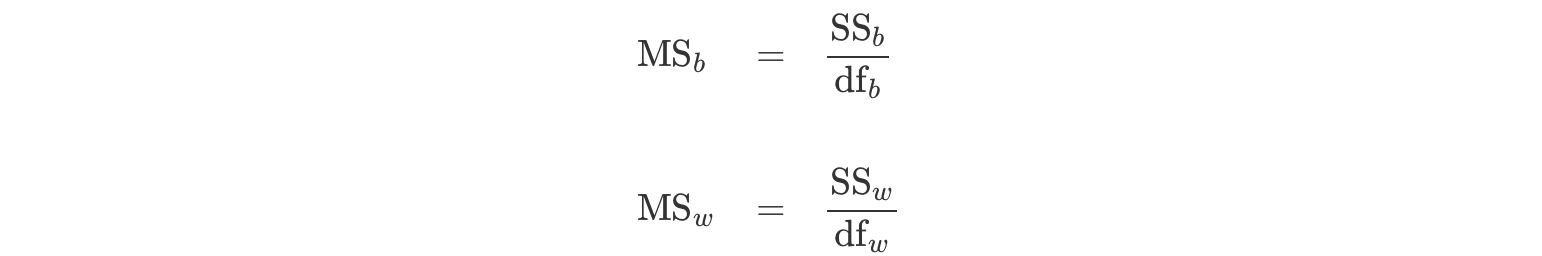
その上で、これら全ての偏差の2乗の値を足し上げると、2117.5となります。これを「全体のばらつきの2乗和」または「ばらつきの総和」と呼びます。
これまでに計算したグループ間の平均のばらつきの2乗和である324.2とグループ内のばらつきの2乗和である1793.3を足し上げると2117.5となりますが、これがまさに今計算した全体のばらつきの2乗和と同じ値になります。
\[\begin{aligned} グループ間のばらつきの和 + グループ内のばらつきの和 = 324.2 + 1793.3 = 2117.5 \end{aligned}\]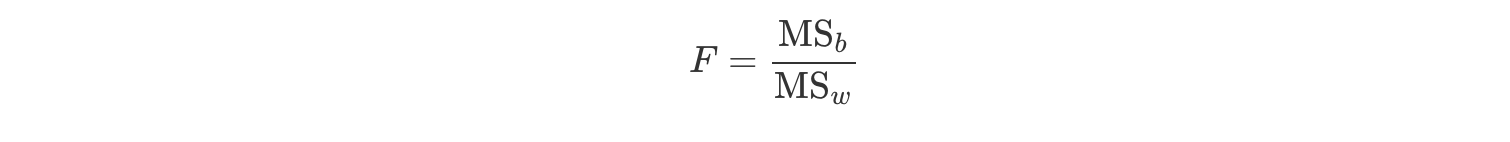
F値の計算
それではここからいよいよ、グループ間の平均のばらつきとグループ内のばらつきの比率であるF値を計算していきたいと思います。
ところで、一つ注意が必要です。このF値の計算に使うばらつきには、これまでのようにグループ間のばらつきの2乗和やグループ内のばらつきの2乗和をそのまま使うのではなく、それらを「平均」したものを使います。
そこでそれぞれの平均をどのように計算するのかを見ていきましょう。
グループ間のばらつきの平均
これまで、グループ間の平均のばらつきの2乗和が324.2と求まっています。そこで、この総量をグループの数で割ることでグループあたりの平均のばらつきの大きさを計算します。この値をグループ間2乗平均と呼びます。
ただここで注意が必要です。例えば学校の例の場合は3つのグループがあるわけですからグループ間2乗和を3で割りたいところです。しかし、これまでにも不偏分散の計算で見てきたように、ここでも手元のデータ(サンプル)から母集団に関するばらつき(分散)を推定したいため、偏りのないグループ間の分散(不偏分散)を求めるためには、3から1を引いた自由度で割る必要があるのです。
ここでの自由度は全体の平均が決まっているのであれば、複数のグループの平均値のうち自由に動かせるものはグループの数(N)から1を引いたものとなります。
\[\begin{aligned} 自由度 = グループの数(N) - 1 \end{aligned}\]今回は3つの平均のばらつきですから、グループの数は3となり、自由度は3から1を引いた2となります。
先ほどの学校のグループ間の平均の2乗和324.2を自由度2で割ると、グループ間の平均のばらつきの2乗平均(グループ間2乗平均)が162.1と算出されます。
\[\begin{aligned} グループ間2乗平均 = \frac{(324.2}{2} = \frac{324.2}{2} = 162.1 \end{aligned}\]グループ間の平均値の差が大きいのであれば、この値は大きくなるでしょう。逆にグループ間の違いが小さいのであれば、小さくなるでしょう。
しかし、この値をもって3つのグループ間の差が統計的に有意であると言えるほど十分に大きいのかどうかは、このグループによる要因以外のばらつき、つまりグループ内のばらつきの平均がどれくらいかによって変わってきます。
グループ内のばらつきの平均
ここまでで、グループ内2乗(平方)和、つまりグループ内のばらつきの総量は1793.3とすでにわかっています。そこで、この総量を全員の人数で割ることでグループ内のばらつきの平均を計算します。この値をグループ内2乗平均と呼びます。
ただここでも、母集団に関するばらつきを推定したいわけですから、偏りのない分散(不偏分散)を求めるためにグループ内ばらつきの2乗和を全員の数で割る代わりに自由度で割る必要があります。
\[\begin{aligned} グループ内のばらつきの2乗平均 = \frac{グループ内ばらつきの2乗和}{自由度} \end{aligned}\]さて、この自由度に関して注意が必要です。
今回は、それぞれの生徒のスコアと全体の平均値との差を計算したのではなく、それぞれの学校の平均値との差を計算しました。ということは、それぞれのグループの平均値がわかっていた場合、その平均値を計算するためには最後の一人以外は自由に値を決めれますが、最後の一人の値は他の人の値が決まってしまえば、自ずと決まります。これがそれぞれのグループで起きます。このことを考慮して自由度を計算すると以下のようになります。
\[\begin{aligned} 自由度 = (学校Aの生徒の数 - 1) + (学校Bの生徒の数 - 1) + (学校Cの生徒の数 - 1) \end{aligned}\]これは以下のようにまとめることができます。
\[\begin{aligned} 自由度 = 学校Aの生徒の数 + 学校Bの生徒の数 + 学校Cの生徒の数 - 3 = 全生徒の数 - 3 \end{aligned}\]そこでグループ内のばらつきの平均(不偏分散)を求める際の自由度は以下のような式で表すことができます。
\[\begin{aligned} 自由度 = N(データ量) - グループの数 \end{aligned}\]これまでにすでに計算されたグループ内2乗和である1793.3をさきほどの自由度27で割ることで、グループ内のばらつきの平均(2乗平均)を計算します。
\[\begin{aligned} グループ内のばらつきの2乗平均 = \frac{グループ内ばらつきの2乗和}{自由度} = \frac{1793.3}{27} = 66.4185... \end{aligned}\]それでは、グループ間のばらつきとグループ内のばらつきが計算できたので、さっそくF値を求めてみましょう。
グループ間のばらつきとグループ内のばらつきの比率
グループ間のばらつきの2乗平均、そしてグループ内のばらつきの2乗平均が求まったので、あとはこれらの比率であるF値を計算するだけです。
\[\begin{aligned} F値 = \frac{グループ間のばらつきの2乗平均}{グループ内のばらつきの2乗平均} \end{aligned}\]先ほどの学校の平均スコアの例では、グループ間の平均値のばらつきは162.1、グループ内のばらつきは約66.42でしたので、それらの比率を計算すると2.44となります。
\[\begin{aligned} F値 = \frac{162.1}{66.42} = 2.44 \end{aligned}\]これが今回の学校のテストの平均の違いの大きさを表すF値となります。
F分布
さて、F値が計算できてもそれだけでは、グループ間の平均値の差が有意なのかどうかは判断できません。私たちが知りたいのはその数値が「平均値に差がない」という帰無仮説を棄却できるほど十分に大きいのかどうかです。そこで必要となるのが、手元のデータから得られたF値かさらに大きい値が出るであろう確率を出してくれるF分布という確率分布です。
同じ母集団から繰り返し複数(たとえば3つ)のサンプルを抽出した上でF値を算出するとそれらのF値のばらつきはこのF分布という確率分布に従うことがわかっています。
このF分布の形は2つの自由度によって変わります。1つはグループの数に関する自由度で、F値の計算をする時の分子に当たるグループ間の平均のばらつきの2乗平均に使われたものです。もう一つはデータの量に関する自由度で、これは分母に当たるグループ内のばらつきの2乗平均に使われたものです。今回はグループの数に関する自由度は2、データ量に関する自由度は27でしたので、その場合は以下のようなF分布となります。
以下は2つの自由度の値を変えた時にF分布の形がどう変わるかをチャートにしたものです。df1がグループ間の自由度、df2がデータ量の自由度の値となります。
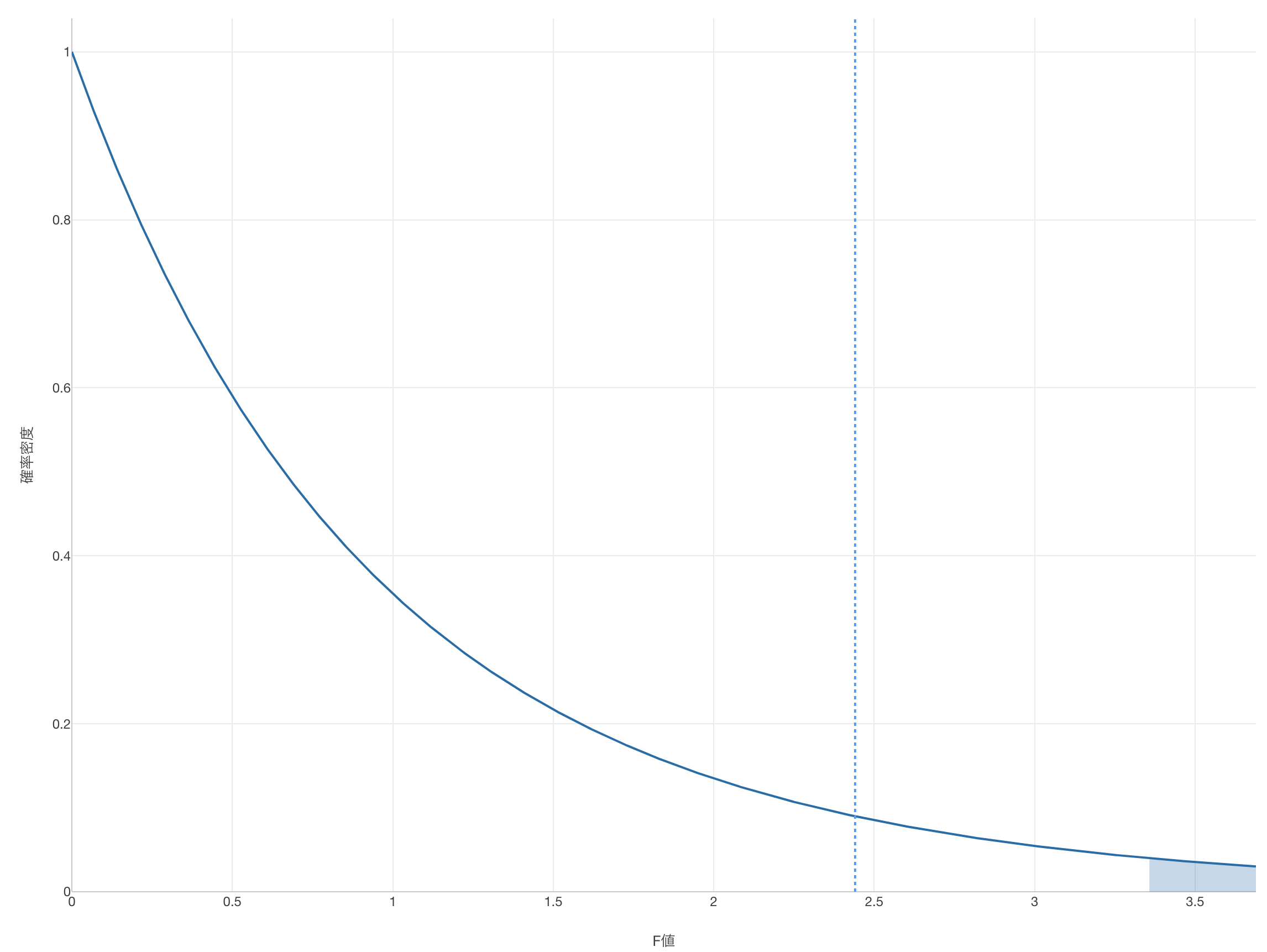
このF分布のX軸はいつも0から始まり値は大きくなるだけです。というのも、F値が比率であるという性質上、値が0よりも小さくなることはないからです。そのためF分布を確率分布として使うANOVA検定はいつも片側検定となります。
そこで、P値の捉え方も、手元のデータから算出されたF値かそれよりも大きい値が得られる確率となります。
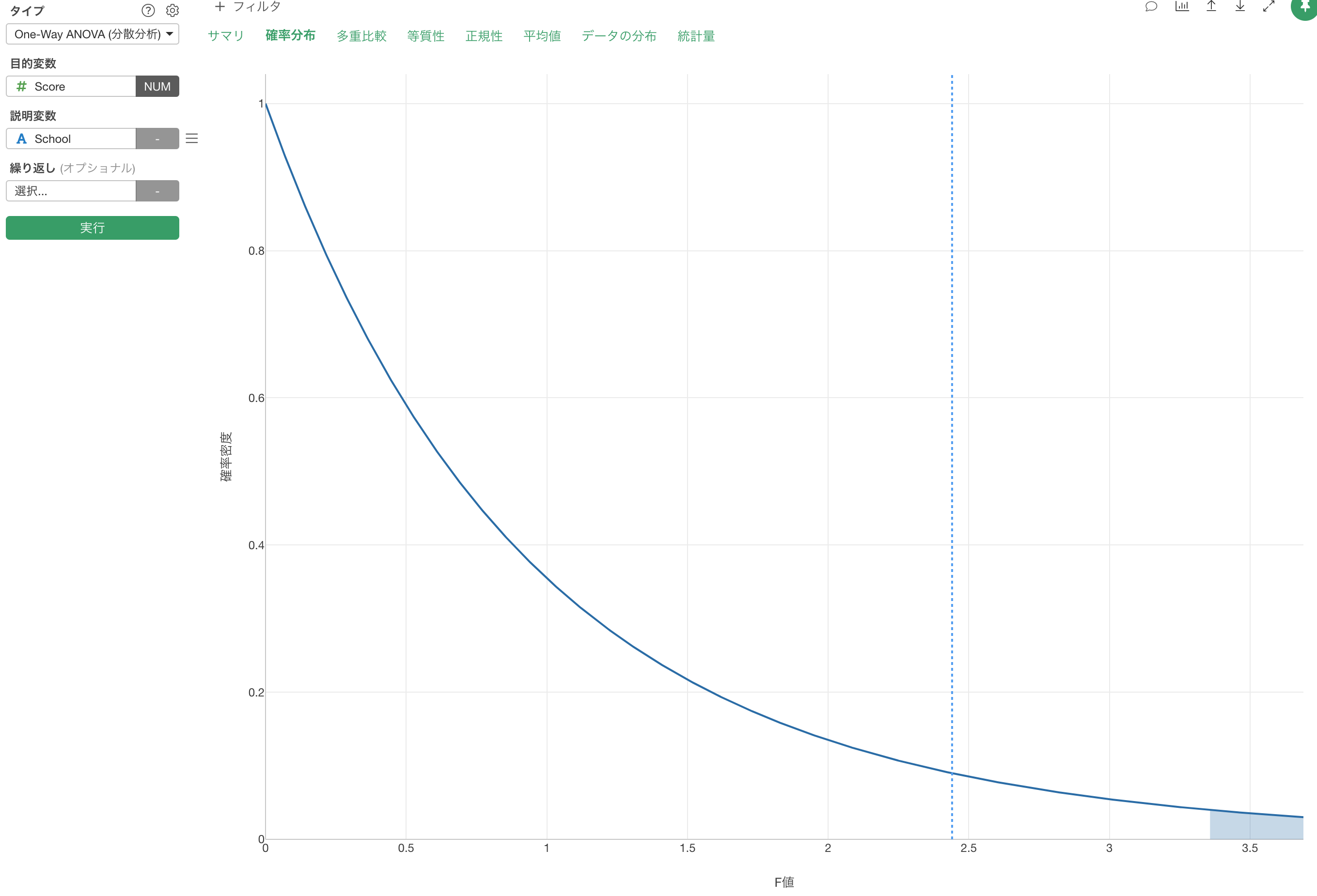
学校のスコアの例では、F値は2.44であるため、もし帰無仮説が正しいのであれば、F値が2.44かそれ以上に大きい値が得られる確率は10.6%ということになります。
P値が求まれば、あとはt検定と同じです。有意水準が5%であれば、もしP値が5%よりも小さければグループ間の平均値の差は有意となります。逆にP値が5%よりも大きければ「平均値に差がない」という帰無仮説を棄却できないため、有意とはなりません。
Let’s do it!
それでは、ここからは実際にExploratoryを使ってANOVA検定を行ってみましょう。そこで、2つのデータを使ってみたいと思います。まず一つ目は今回ANOVA検定におけるF値の計算をするさいに見てきた学校の成績データです。これまでマニュアルでやってきた計算の答えがあっているのかを確認してみましょう。
その後に、これまで使ってきた従業員データを使ってANOVA検定を行ってみたいと思います。
学校の成績データ
学校の成績データはこちらからダウンロードできます。ダウンロードしたデータはExploratoryの方にインポートしてください。
インポートが終われば「学校の成績」データフレームを開き、「アナリティクス」ビューに移ります。
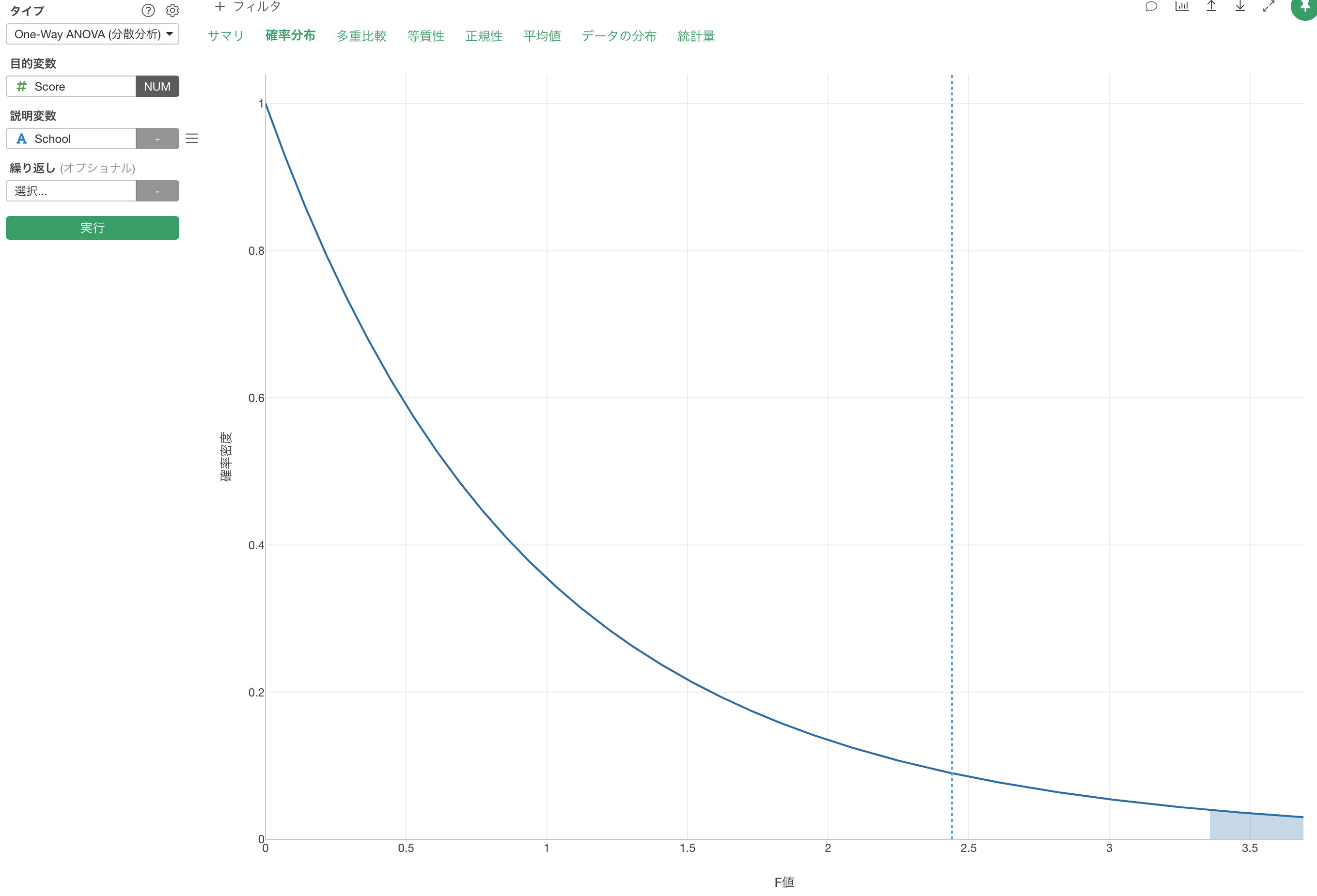
そしてタイプに「One-Way ANOVA(分散分析)」を選び、目的変数に「Score」を、説明変数に「School」を選びます。
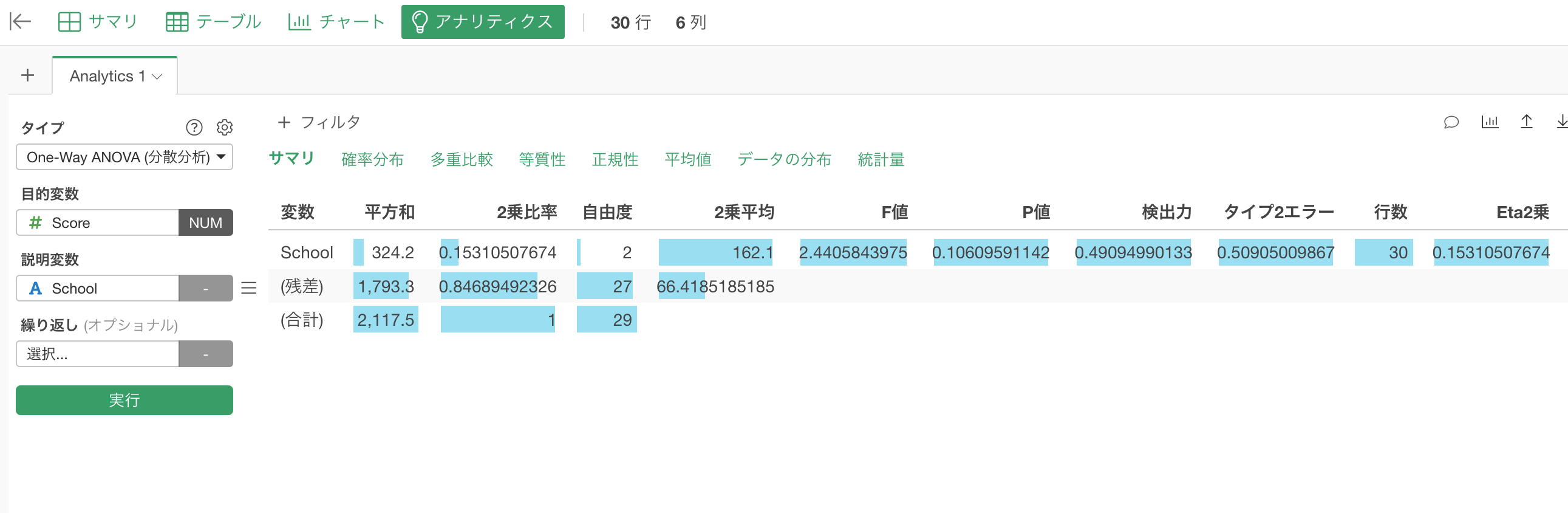
「実行」ボタンをクリックすると、「サマリ」タブの下にこれまでに計算してきた数値が表示されているのを確認することができます。

結論から言うと、P値が0.106、つまり10.6%なため、有意水準を5%とすると帰無仮説を棄却できません。つまりこれらの学校の平均値には統計的に有意と言えるほどの差はないということになります。
このP値の10.6%という値は、F分布という確率分布においてF値の列にある2.44という数値かそれ以上に大きな数値が得られる確率として算出されたものです。帰無仮説である「これらの学校の平均値の間には差がない」が正しいとすると、それでもこのデータに見られるような違いが起きる確率は10.6%だということです。
このF値がF分布のどこに位置するかについては確率分布のタブの下で見ることができます。
今回のANOVA検定においては実質的にはこれでおしまいですが、せっかくですので、今回のP値の算出する元となったF値の計算過程を見てみましょう。
F値の計算
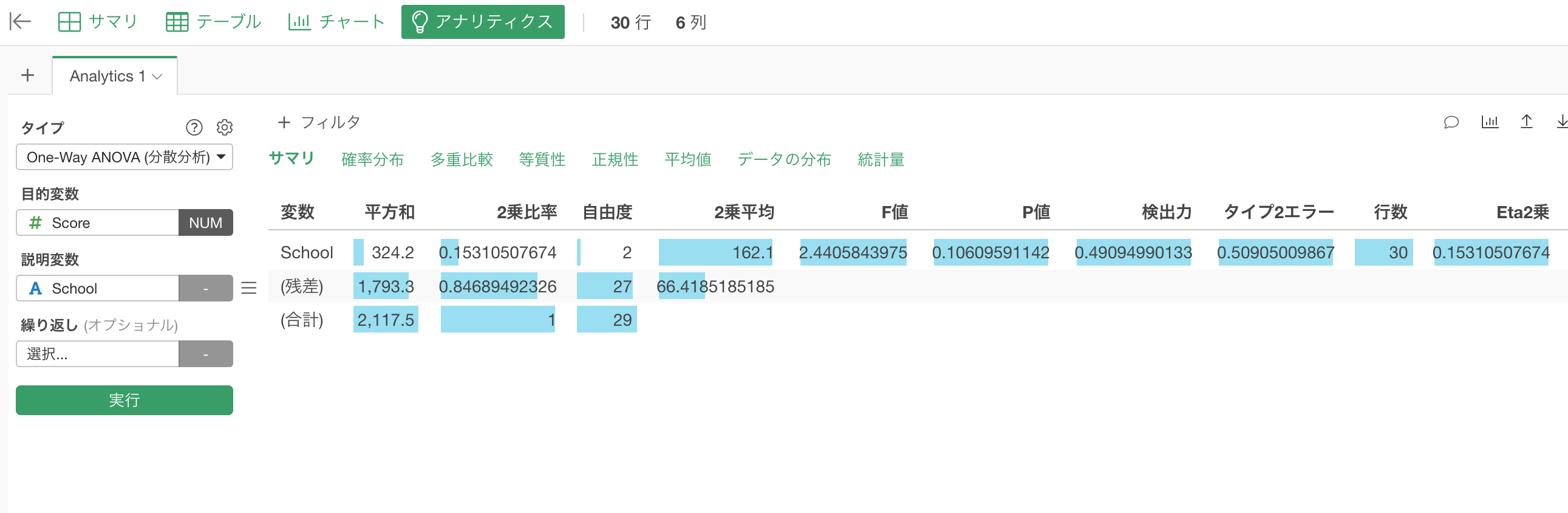
F値の計算過程はサマリ・タブの下で確認することができます。

すでに説明したようにF値とはグループ間の平均のばらつき(分散)の大きさをグループ内のばらつき(分散)の大きさと比べた比率です。
ばらつきの2乗和
まず、1行目は変数がSchool(学校)と書いてありますが、この行がグループ間の平均値のばらつきに関する情報となります。そして2行目がSchool(学校)以外のばらつき、つまりグループ内のばらつきに関する情報です。3行目は全体のばらつきに関する情報です。

2乗和の列の下にはそれぞれのばらつきの2乗和の値が表示されています。学校間のばらつきの2乗和(1行目)と学校内の2乗和(2行目)を足し上げると全体の2乗和(3行目)となります。
ばらつきの2乗平均
2乗和を自由度で割ったものが2乗平均です。学校間の2乗和324.2を自由度2で割ると2乗平均の162.1となります。同じく、学校内の2乗和1793.3を自由度27で割ると2乗平均の66.41…が求まります。
F値の計算
最後に、学校間の2乗平均162.1を学校内の2乗平均66.41…で割ると、F値2.4405…がもとまります。
従業員データを使ったANOVA分析
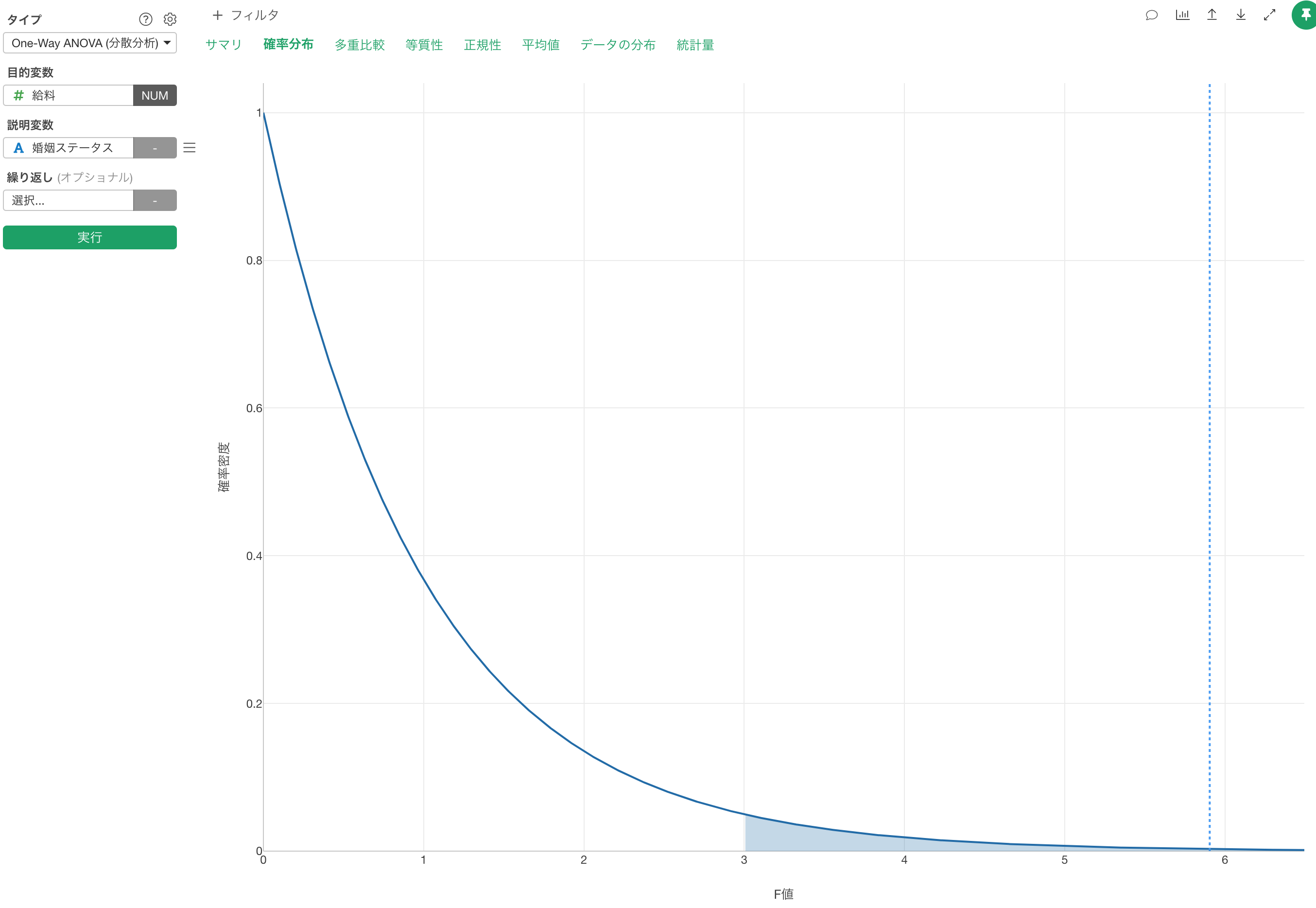
ここではもう1つANOVA検定を行ってみたいと思います。従業員データに「婚姻ステータス」という変数がありますが、婚姻ステータスの違いによって給料が変わるのか、その違いは統計的に有意と言えるのかどうか、ANOVA検定を使って調べてみましょう。
プラスボタンをクリックして新しいアナリティクスのタブを開きます。
タイプに「One-Way ANOVA(分散分析)」を選び、目的変数に「給料」、説明変数に「婚姻ステータス」を選び、「実行」ボタンをクリックします。

まずは、P値を確認すると0.2%(0.00279…)ですので、有意水準が5%とするとそれよりも小さいため、婚姻ステータス間で給料の平均値の違いは有意であると判断できます。このP値の算出の元となったF値は5.90ですが、この値がF分布においてどのあたりに来るかは「確率」タブの下で確認することができます。