One-Way ANOVAの前提条件
他の統計的検定と同様に,分散分析もデータに対するいくつかの仮定に依存しています。とくに重要な仮定は以下の3つです。
- 正規性
- 分散の等質性
- 独立性
これまで見てきたどの計算もこの仮定なしには正しく機能しないからです。
より正確には,それでもすべての計算をして F 統計量にたどり着くこと自体はできるのですが,その F 統計量で実際に私たちが測定したいものを測定できているという保証が得られないのです。
これはその F 統計量を用いた検定を基に引き出された結論は,どれも間違っている可能性があるということを意味します。
では,この残差に関する仮定が正しいことをどうやって確認したらいいのでしょう。前述の通り,この仮定には3つの異なる主張が含まれていますので,それらを別々に見ていくことにしましょう。
正規性
残差は正規分布していることが仮定されています。正規正検定(シャピロ・ウィルク検定)で評価できます。
分散の等質性
母集団の標準偏差に関しては,それぞれのグループが別々の標準偏差を持つ( σk )のではなく,1つの値(つまり σ )しかないという点に注意してください。これは分散の等質性(等分散性)の仮説とよばれます。分散分析では,母集団の標準偏差はすべてのグループで同じであると仮定されています。
独立性
分散の等質性の確認方法
等分散性の仮定を検定する方法はいくつかあります。その中でも論文などでもっとも一般的に使用されているルビーン検定と,それに深く関連したブラウン・フォーサイス検定について説明します。
ルビーン検定は驚くほど単純です。私たちの手元に Yik 個の目的変数があるとしましょう。私たちがすべきことは,グループ平均値からの偏差の絶対値に対応した新しい変数を定義することだけなのです。ここでは新しい変数を Zik と表しましょう。
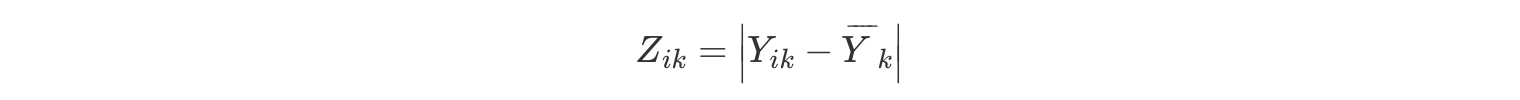
さて,これが何の役に立つのでしょうか。まず, Zik が一体何なのか,私たちが何を検定しようとしているのかについて少し考えてみましょう。 Zik の値は, k 番目のグループにおける i 番目の観測値がそのグループ平均値から離れている程度を表します。そして私たちの帰無仮説は「すべてのグループで分散が同じである」というもので,これはつまり,グループ平均値からの全体的な偏差がすべてのグループで同じであるということです。ということで,ルビーン検定の帰無仮説は「 Z の母集団平均値はすべてのグループで同じである」というものになるのです。そして私たちに必要なのは,「すべてのグループで平均値が同じである」という帰無仮説に対する統計的検定です。これに見覚えはないですか? そうです。これは分散分析です。つまり,ルビーン検定とは,新しく作成した変数 Zik に対して分散分析をするのと同じなのです。
ではブラウン・フォーサイス検定はどうでしょう。何か際だった違いがあるのでしょうか。ありません。ルビーン検定との違いは, Z 変数の値の求め方が少し違うということだけです。この検定では,グループの平均値の代わりに中央値からの偏差を使用するのです。これがブラウン・フォーサイス検定です。
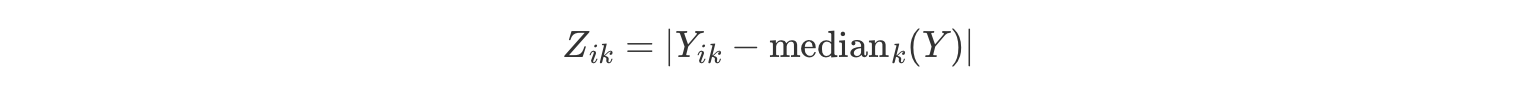
mediank(Y) はグループkの中央値です。標準的なルビーン検定の場合もブラウン・フォーサイス検定の場合も,検定統計量(これはFと書かれることもあればWと書かれることもあります)は通常の分散分析で計算されるF統計量とまったく同じ方法で算出されます。ただ,Yikの代わりにZikが使用されているだけなのです。
Exploratoryを使ったルビーン検定
Exploratoryの中ではルビーン検定手法を使った等質性の検定は自動で行われていて、「等質性検定」のタブの下でその結果を確認することができます。

検定結果は有意でない(P値が0.12)ため、「すべてのグループで平均値が同じである」という帰無仮説を棄却できない、つまり分散は等質であるという結論となります。等質性の仮定については問題なさそうです。
ブラウン・フォーサイス検定手法を使って等質性の検定を行いたい場合は、プロパティより手法を変更できます。
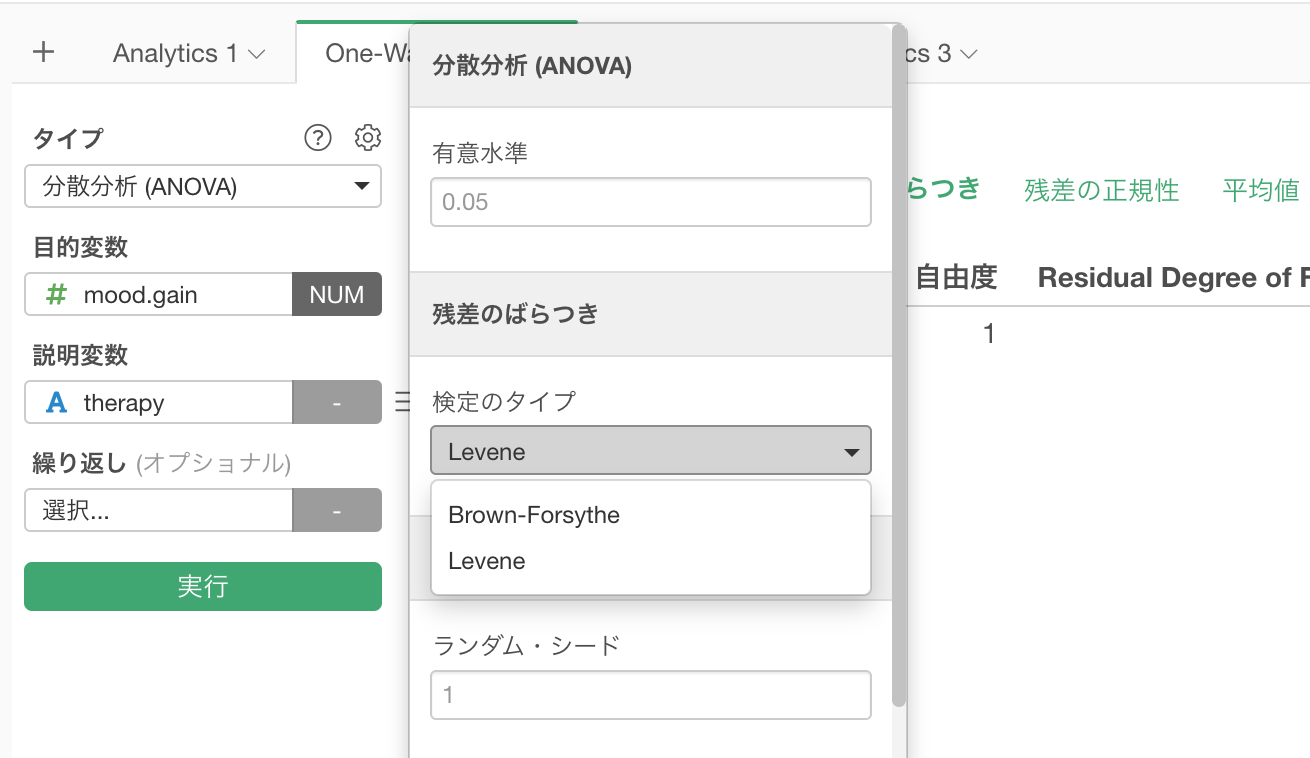
この場合、P値やF値の値はルビーン検定に比べて変わりますが、結果は同じです。

検定結果は有意でない(P値が0.13)ため、「すべてのグループで平均値が同じである」という帰無仮説を棄却できない、つまり分散は等質であるという結論となります。
正規性の仮定の確認方法
正規性の仮定については、「正規性の検定」タブの下でシャピロ・ウィルク検定手法の結果を確認することができます。

検定結果は有意でない(P値が0.10)ため、「正規分布している」という帰無仮説を棄却できないため、正規分布している、つまり正規性の仮定も満たしていることになります。