カイ2乗検定
女子生徒:これまでの検定では目的変数が数値型の列でした。でも、今回の従業員データのように別のデータ型もあります。その場合はどうすれば良いのですか?
先生:いい質問ですね。これまでは複数のグループ間で給料などのような数値における違いがあるかどうかを検定してきたけど、例えば離職のようにTRUEかFALSEのような値を持つロジカル型、また結婚ステータスのように独身、既婚、離婚といった値を持つ文字列型の変数における違いもありますね。
男子生徒:でもそれは文字列だから平均値などを計算できないので無理なのではないですか?
先生:例えば離職の場合、男女間で違いがあると思いますか?その場合、その違いってどういった数値で表されると思いますか?
女子生徒:男性が200人離職していて、女性が100人離職しているので男性の方が多いですね。
男子生徒:でも、この会社は男性の方が1000人いて女性は300人しかいないので、男性の方が多いとは言えないんじゃないかな。ここは割合に直した方がいいんじゃないかな。例えば男性で離職した人たちの全体に占める割合、つまり離職率は15%、しかし女性の離職率は17%だとすると、女性の方が離職しやすいと言えますね。
先生:そういうことです。目的変数がロジカル型や文字列型の場合は割合にしてあげることで、数値となります。そしてこの場合問題となるのは、この15%と17%の違いは有意な違いなのかどうかということなのです。そして、このようなときに使うことができる仮説検定の手法がカイ2乗検定なのです。
カイ2乗検定の仕組み
カイ2乗検定は2つのカテゴリー型の変数に関係があるかどうかを調べる時に使える統計的検定手法です。カテゴリー型には文字列型やロジカル型が含まれます。ここでの興味の対象、つまり目的変数は割合となって表されます。
例えば目的変数がロジカル型の離職の場合、
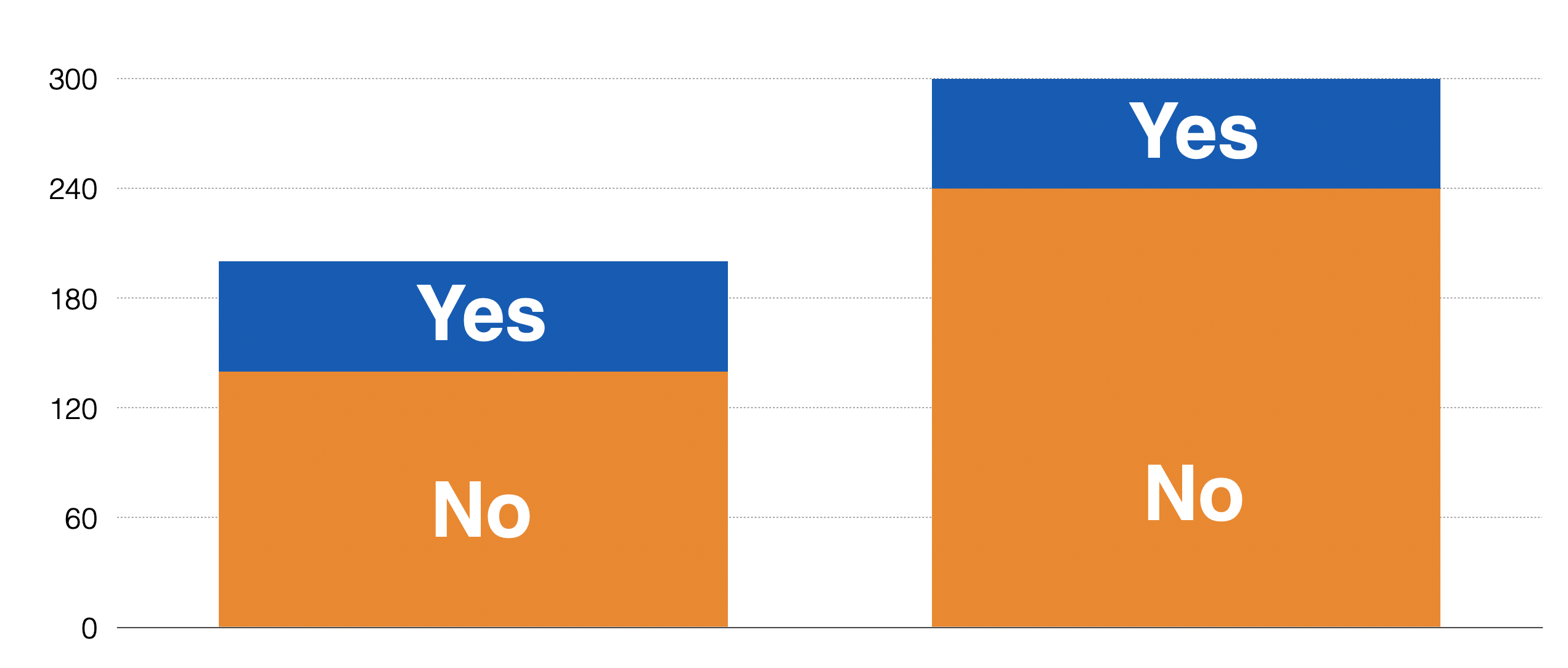
これを割合として表すと以下のようになります。
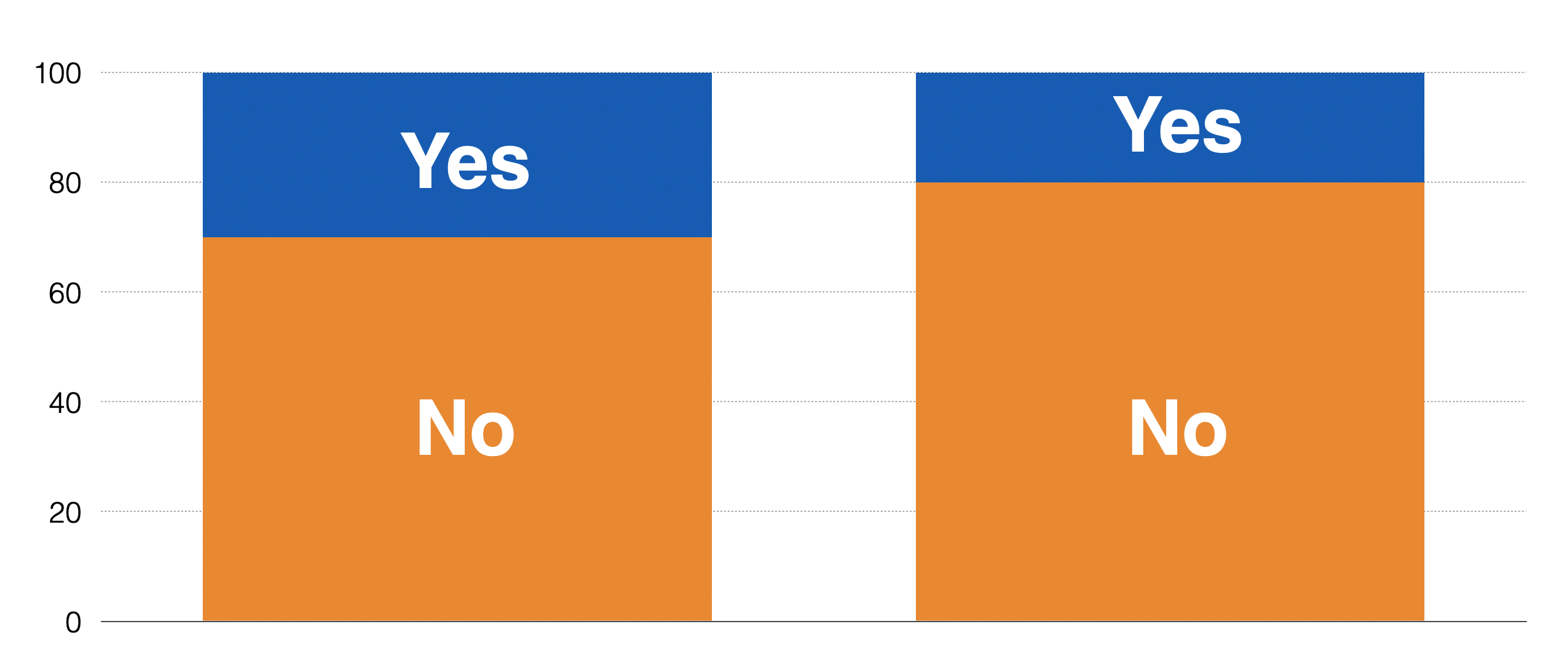
目的変数のグループの割合構成が、説明変数のグループ間で異なるのかどうかをテストしたいということです。
帰無仮説
ですのでこの場合の帰無仮説は、説明変数の複数のグループ間で目的変数の割合は同じ、変わらないとなります。
例えば上記の例の場合、男女間で離職率は変わらないというのが帰無仮説です。
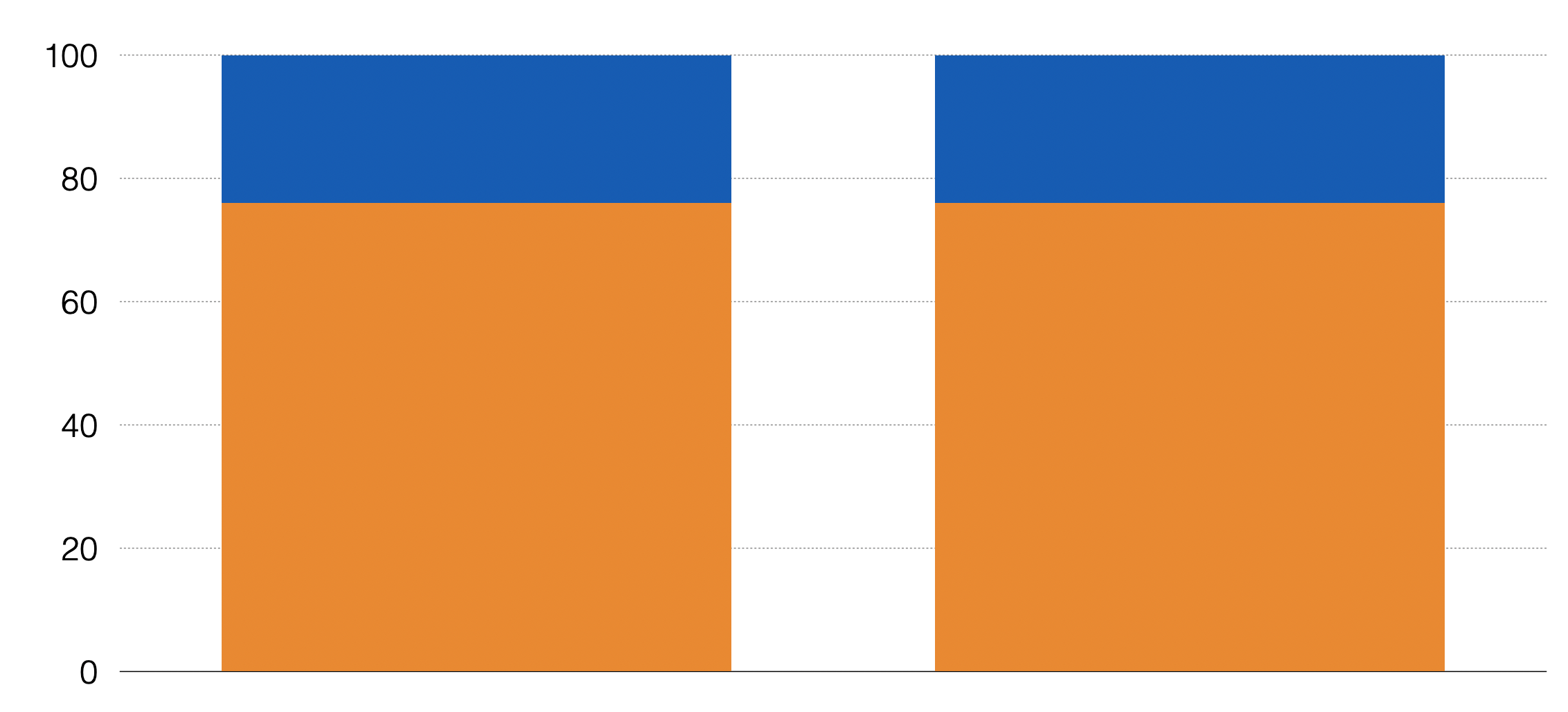
しかしデータはばらつくわけですから、離職率が全く同じということはありません。そこでどれくらいの大きさであればただのデータのばらつきで片付けることができ、どれくらいの大きさであればその違いは帰無仮説を棄却するに足るほど大きいのかを調べる必要があるのです。
そこで、その違いの大きさを測る指標としてカイ2乗というものを計算する必要があります。
カイ2乗値
まず、最初に覚えておいて欲しいのはカイ2乗値とはずれの大きさの指標だということです。2つのカテゴリー型の変数間に関係がなければ、それらを比率で表すと同じであるはずです。
<image>
この同じ比率である状態に比べて、手元にあるデータの比率はどれくらいずれているのかを示すものがカイ2乗値です。そのためこの値が大きければずれが大きいと言うことで、逆に小さければずれがちいさいということです。そしてずれが大きければ、その分関係がないという帰無仮説を棄却できる可能性が高くなるということです。
帰無仮説が正しいとする時に期待される状態
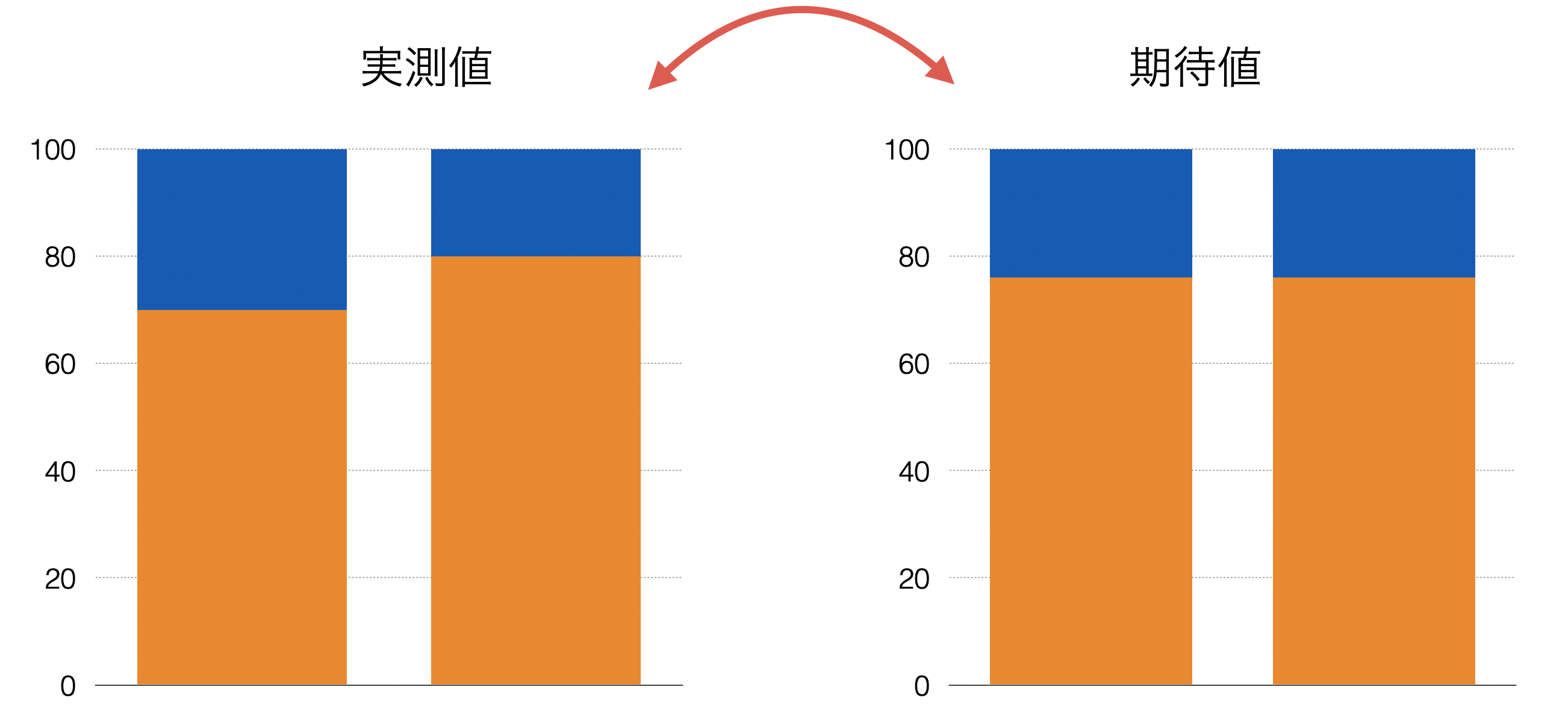
それではこの違いがないという期待されている値をどのように算出すればよいのでしょうか?実はこれは意外に単純です。例えばこのようなデータの場合を考えてみましょう。
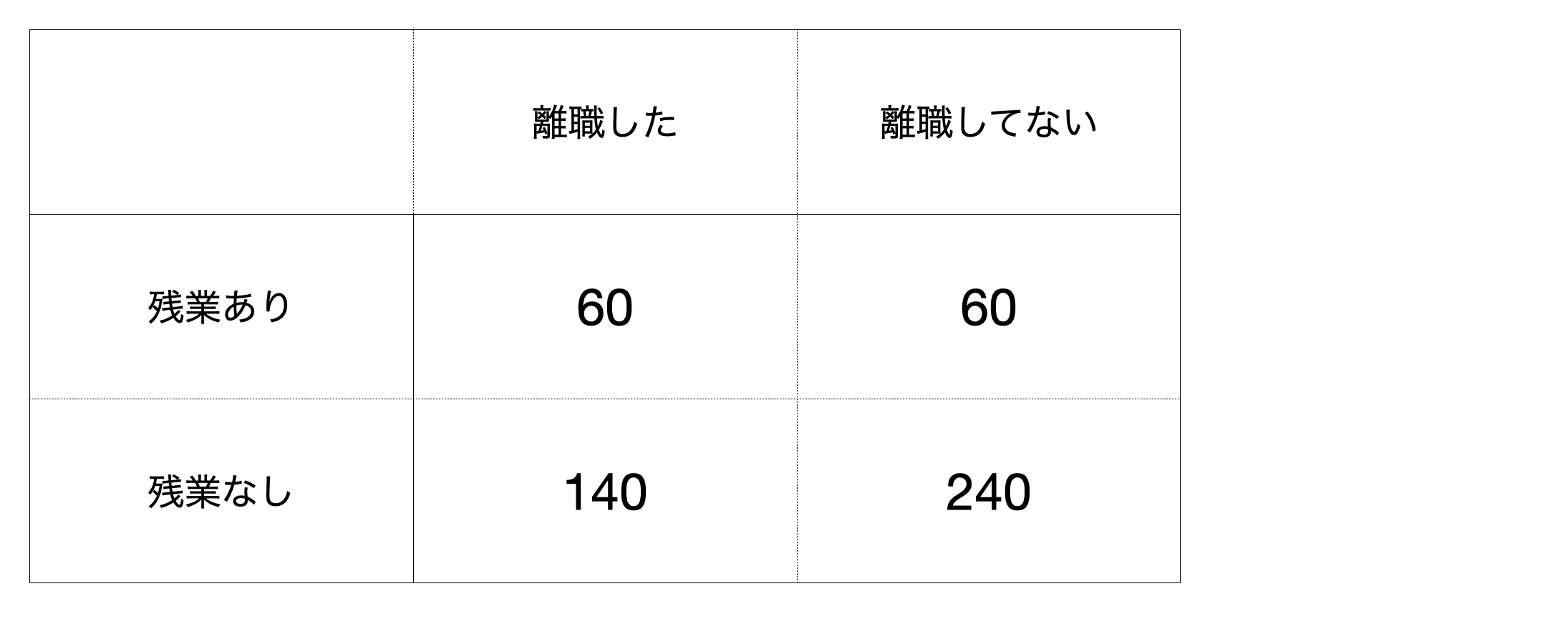
この場合離職した人たちの割合は24%、してない人たちは76%です。
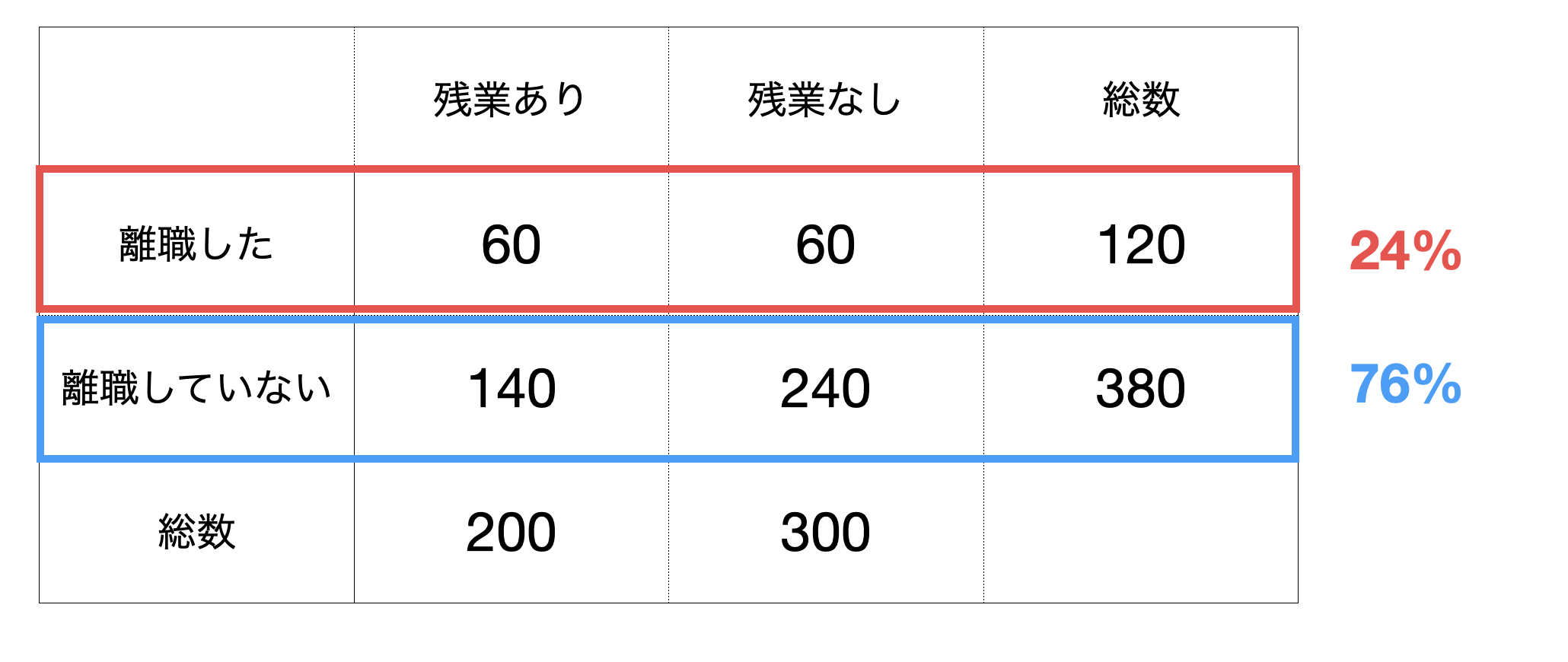
もし残業したかどうかが離職するかどうかに関係ないのだとしたら、残業している人たちのグループもしていない人たちのグループも、離職した人たちとしてない人たちのの割合はそれぞれ24%、76%となるはずです。
その場合、残業した人たちは200人いるので、そのうちの24%が離職した、76%が離職していないとなるでしょう。
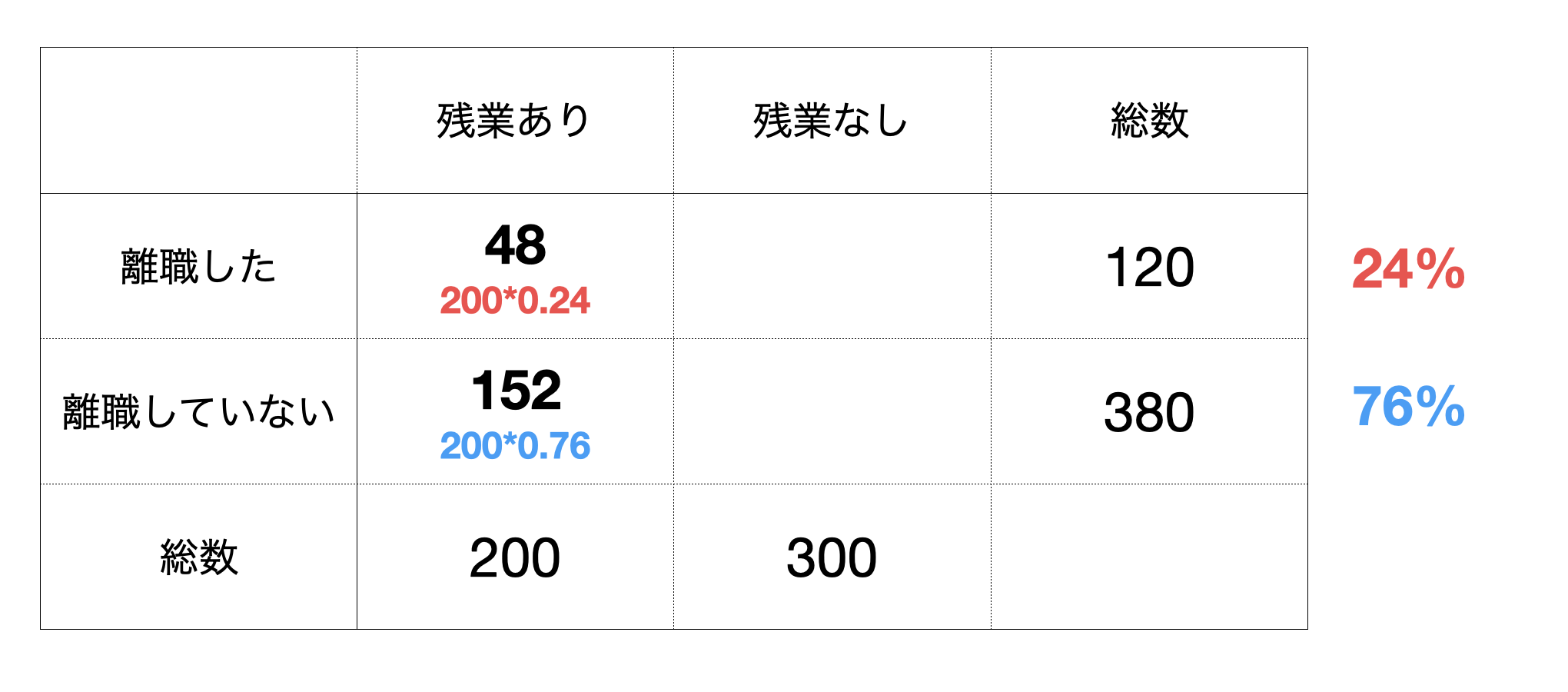
同じように、残業してない人たちは300人いるので、そのうちの24%が離職した、76%が離職していないとなるでしょう。
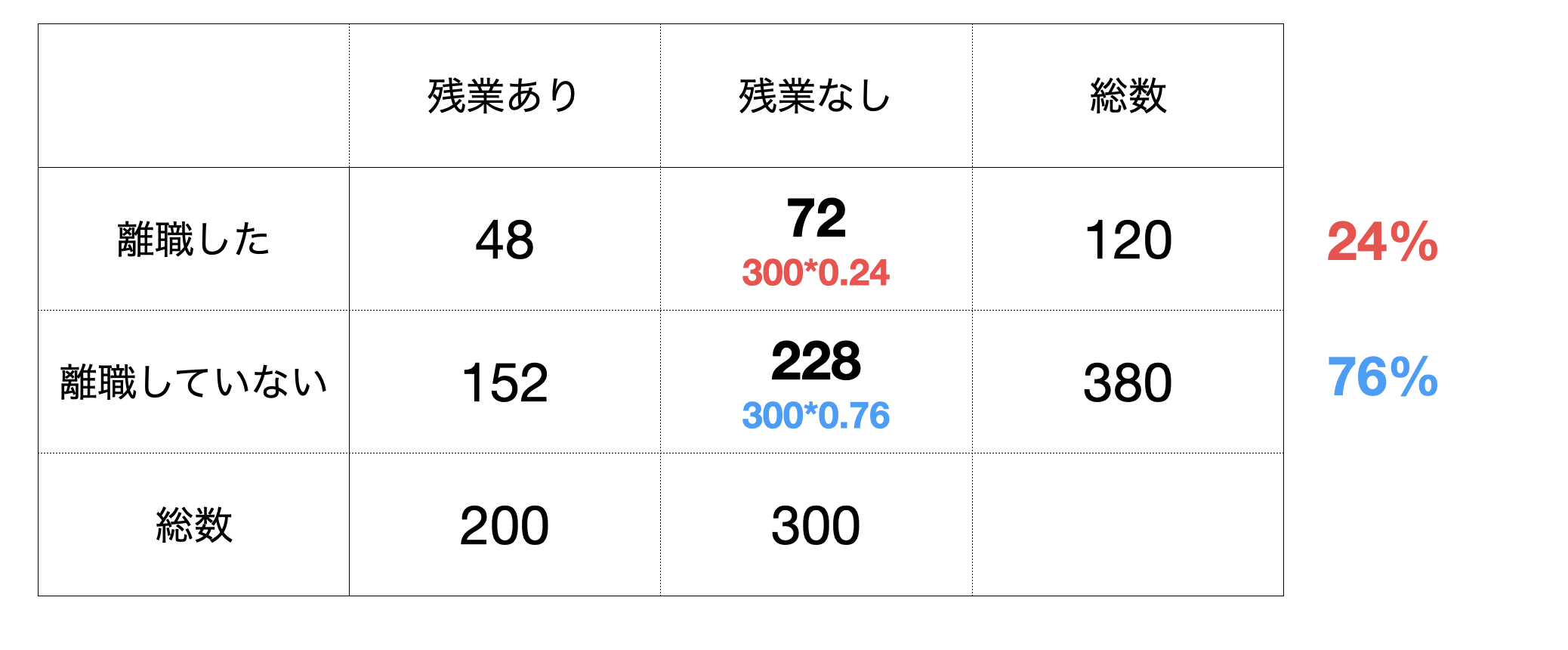
こうして帰無仮説が正しいのであれば、つまり残業と離職が関係ないというのだれば期待される人数構成が決まりました。もちろん、残業あり、残業なしにおける離職率はどちらも24%となります。

さてここで期待値が決まったわけですから、次は実測値、つまり手元にあるデータがどれだけこの期待値とずれているかを数値と表すことになります。
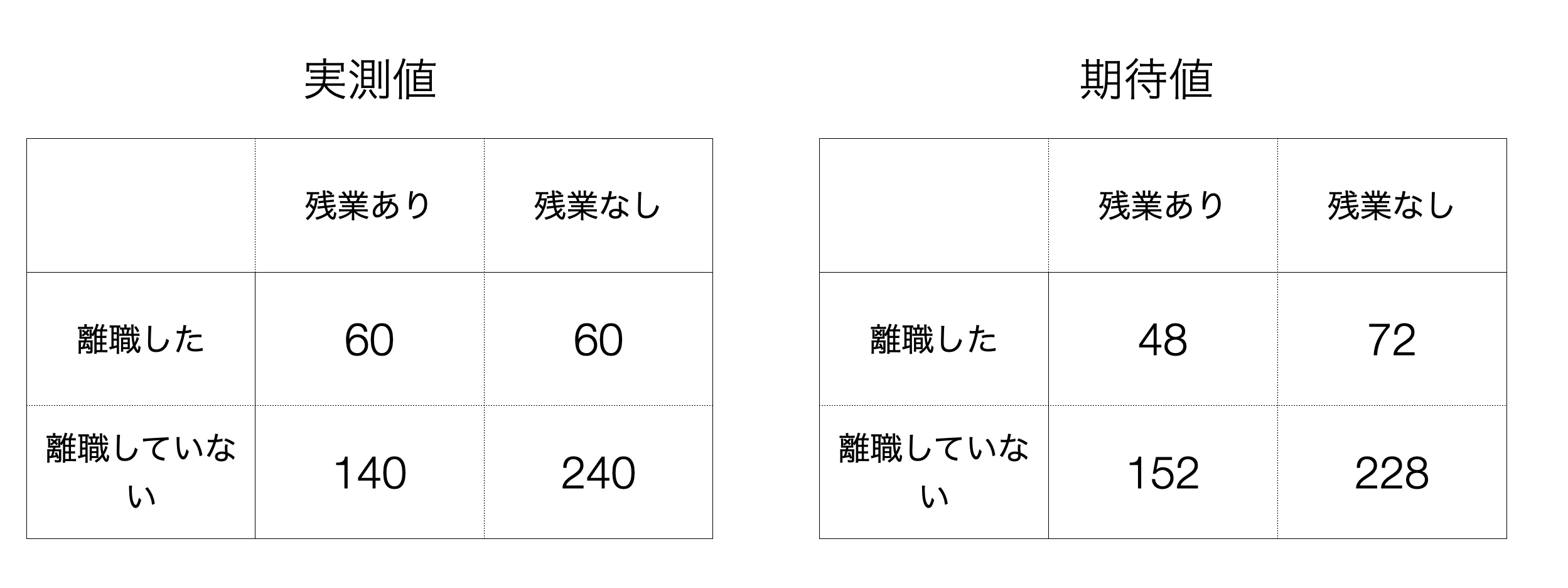
これも比較的単純です。それぞれの組み合わせの数字を引き算し、それらの平均値を求めるだけです。
例えば残業ありで転職した人たちの場合、実測値は60ですが期待値は48なので、その差は12となります。これを全ての組み合わせで行い足し上げます。
((60-48) + (140-152) + (60-72) + (240-228)) = 0ところが、単純にずれを計算して足し上げると0となってしまいます。これは標準偏差の計算の時にも同じようなことがありました。そこで標準偏差の計算の時と同じようにここでも先に2乗してから足し上げます。
\[\begin{aligned} (60-48)^2 + (140-152)^2 + (60-72)^2 + (240-228)^2 = 576 \end{aligned}\]これがずれの値です。ただこの数値はずれを表しているのですが、1つ問題があります。というのももし元の値のスケールが大きい場合、例えば2万人、20万人いるデータを扱っていた場合、このずれの数値は自ずとかなり大きな数値になります。
そこで元のデータのスケールに関わらず、単純にずれの大きさを表すために「標準化」をしてみたいと思います。そのためには、それぞれの組み合わせで期待される数値の何倍ほどずれがあるかと言うことを計算すればよいことになります。
例えば残業ありで転職した人たちの場合、実測値と期待値の差は12、それを2乗した数値は144です。この144は期待値である48からすると3倍大きい数値となります。これをそれぞれの組み合わせの数値に対して行い、最後に足し上げます。
144/48 + 144/72 + 144/152 + 144/228 = 6.579この6.579という算出された数値がカイ2乗値となります。
カイ2乗分布
同じ母集団のデータから2つのグループをランダムに抽出し、それぞれのグループの割合を出し、それを期待値と比べてカイ2乗値を計算するということを何度も繰り返すと、これらのカイ2乗値はカイ2乗分布という確率分布にしたがいます。
ただこのカイ2乗分布はt検定やANOVA検定の時に見た確率分布と同じで自由度によって形が変わってきます。
以下は自由度1から15までのカイ2乗分布を表したものです。
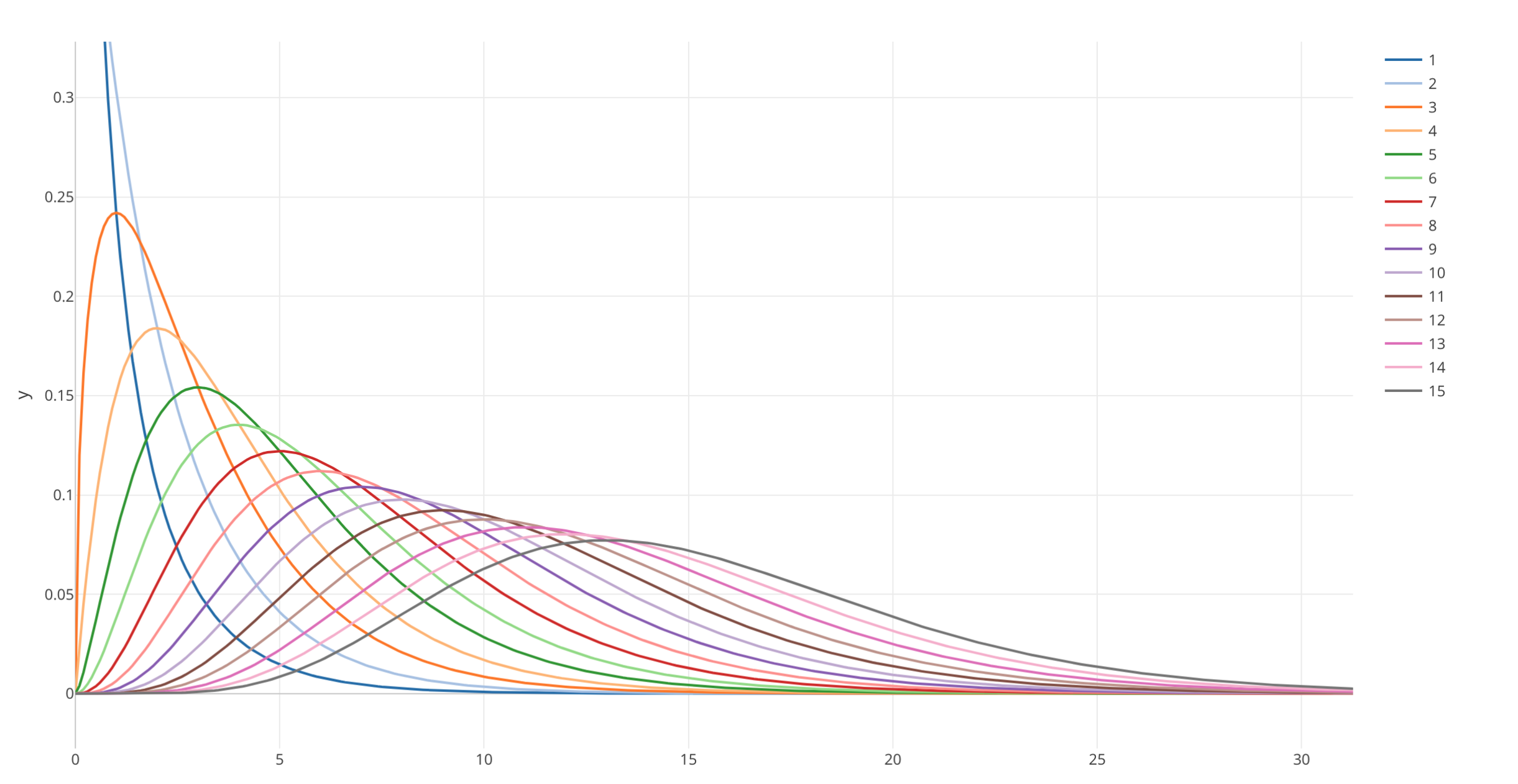
カイ2乗分布における自由度はそれぞれの変数のカテゴリーの数から1を引いたものです。
例えば上記の例では残業という変数にはTRUEとFALSEの2つの値しかありませんが、そのうち1つが決まるとあとは自ずと決まります。そこで2から1を引いた1が自由度ということになります。離職も同じでTRUEとFALSEの2つの値しかないので、自由度は1となります。
そしてこれらを掛け合わせた1が残業と離職の関係における自由度となります。
(2 - 1) x (2 - 1) = 1もし職種と結婚ステータスの関係を調べているのであれば、そのさいは職種が9、結婚ステータスが3つの値となるので、自由度は12となります。
(9 - 1) x (3 - 1) = 12今回は残業と離職の関係ですから自由度は1なので以下のようなカイ2乗分布を使うことになります。
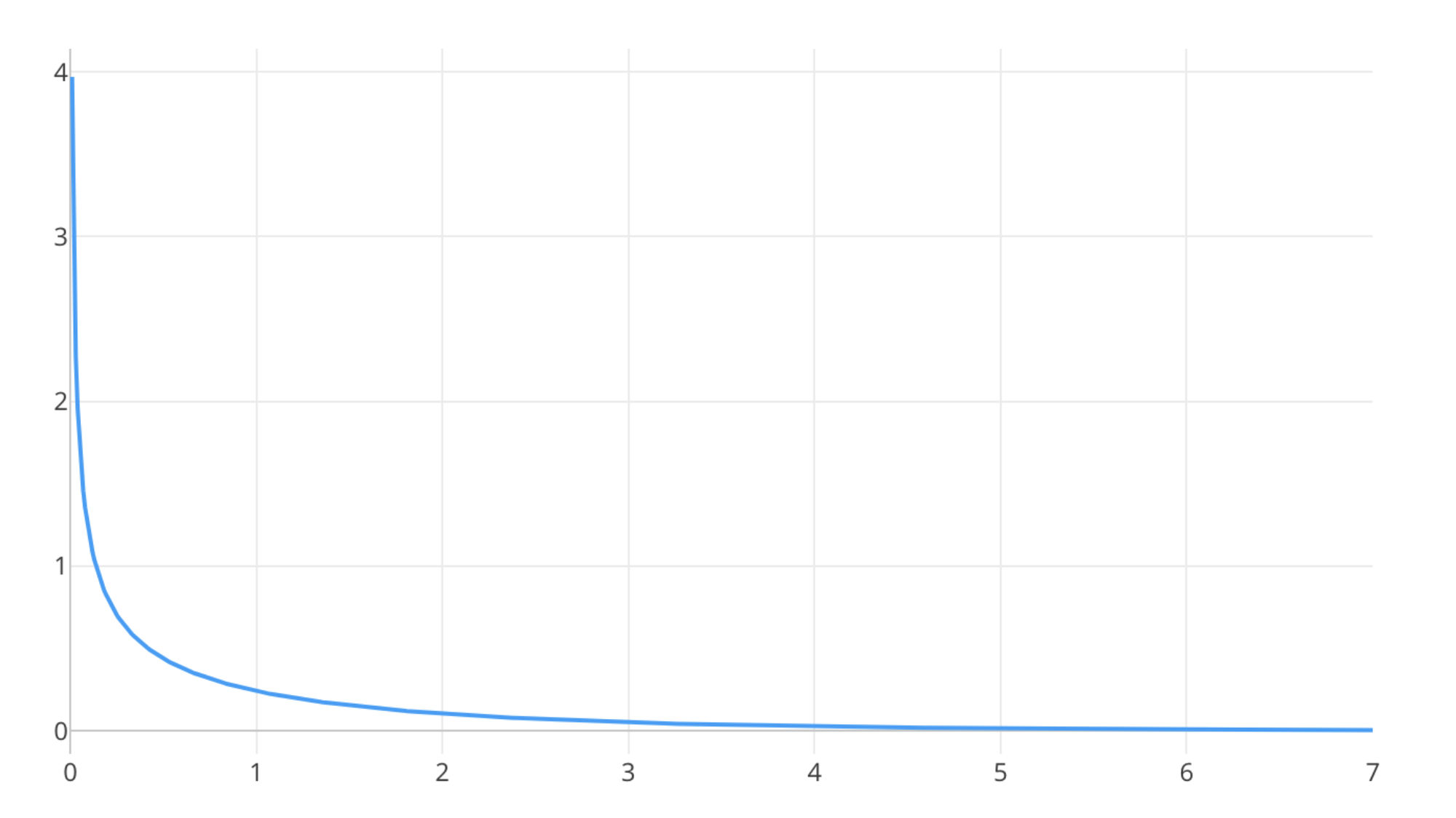
この分布を使って得られたカイ2乗値かそれよりも大きい値が得られる確率、つまりP値を求めることになります。これはカイ2乗値よりも右側のカイ2乗曲線の下の面積となります。
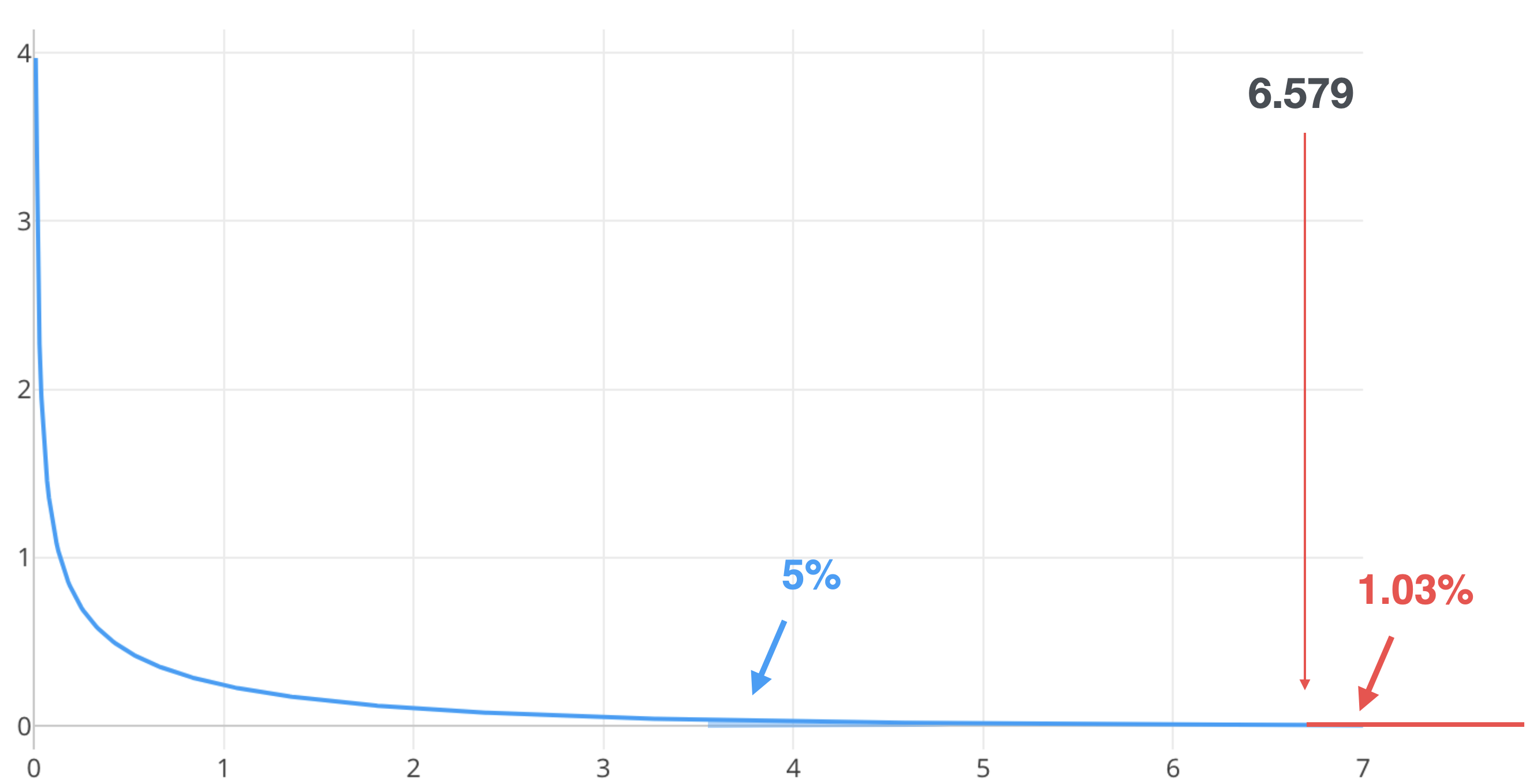
そしてこのP値が棄却水準である5%よりも低ければ、帰無仮説を棄却することができるため、今回の場合であれば残業と離職の関係は有意だと意思決定することができます。逆に、5%よりも高ければ、帰無仮説を棄却できないため有意だとは言えません。
Let’s do it
もちろん、これまでに見てきたのはカイ2乗検定を行う時にどのように統計量であるカイ2乗値やP値を算出するのかという概念を説明してきましたが、実際にみなさんがこうした計算を行うことはありません。そこで実際にExploratoryを使ってカイ2乗検定を行い、その結果を解釈してみましょう。
Exploratoryを使ってカイ2乗検定を行う
まずはアナリティクス・ビューの下に行きます。
カイ2乗検定を選び、「離職」を目的変数に、「残業」を説明変数に選び、実行ボタンを推します。すると以下のような結果が出てきます。
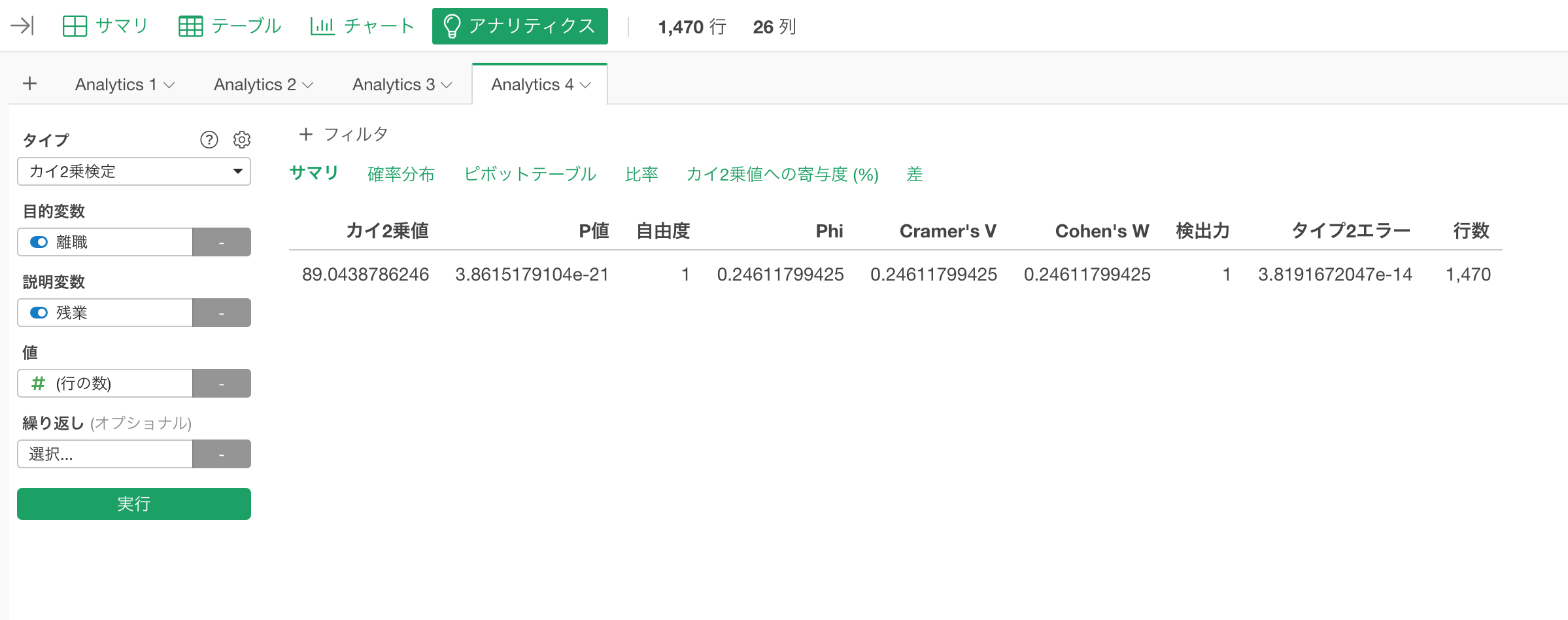
この場合のカイ2乗値は89.04となっています。この値がカイ2乗分布のどのあたりに来るかというのは確率分布のタブの下で確認することができます。
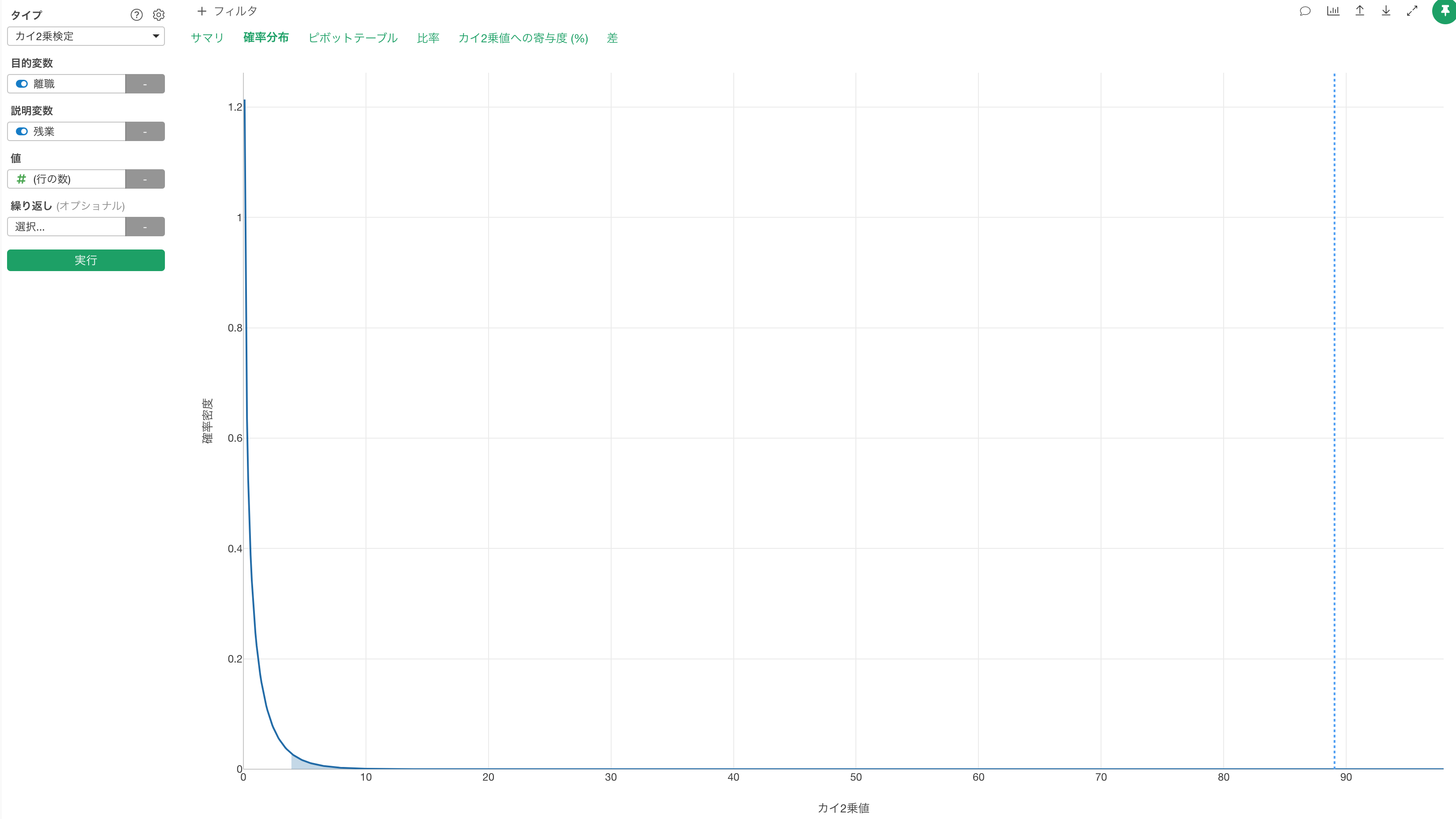
かなり右の方に来ているので、おそらく有意だろうと想定できます。というのも、このカイ2乗値からさらに右の方へ行く部分の曲線の下の面積の割合ですから相当小さそうです。
サマリ・タブの下でP値が確認できますが値が3.8615179104e-21となっています。右の方にeという値が入っている数値は指数標記というものです。
一般的にはマイナスとプラスの場合があるのですが、仮説検定のP値にはたまに出てくる数値でその場合にはいつもマイナスです。マイナスは0.1の何乗かということを表します。今回のようにe-21ということは0.1の21乗ということになり、0が21個並んだ後にeの左側に買われている数字、つまりこの場合は3.8615179104が来るということになります。
あまりにも小さくまともに0を書いていると書く場所が失くなるためこういった標記方法で記されています。eを見れば、それはかなり小さい数値だということで、一般の感覚だとほぼゼロに近いというものです。
いつものように5%の棄却水準を使うと、それよりも低いので帰無仮説である「残業と離職は関係がない」という帰無仮説を棄却し、有意だと判断することができます。
比率タブに行くと実際手元のデータの目的変数と説明変数の関係がどのようになっているかを確認することができます。
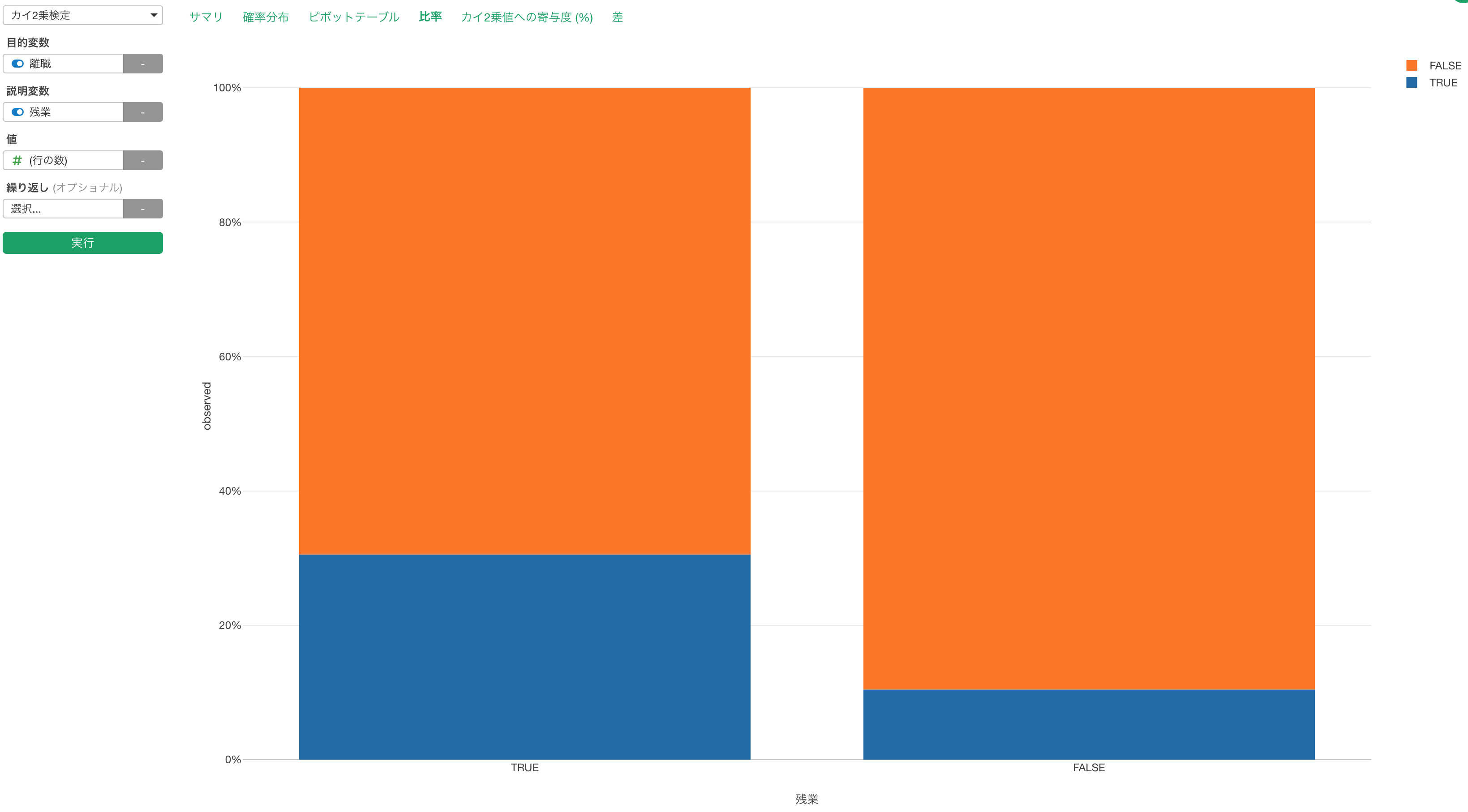
効果量
これまでのt検定やANOVA検定などでも見てきましたが、ここでも効果量というものがあります。カイ2乗検定とはずれがどれだけ大きいのかですが、この数値を調整することで効果量を計算します。
いくつかのタイプの効果量があるのですが、ここでは一般的によく使われるクラメールのVを紹介します。ただそのためにはまずPhi(ファイ)を最初に紹介する必要があります。
Phiの計算方法はカイ2乗値をデータ数で割って、ルートをするだけです。
\[\begin{aligned} Phi = \sqrt{\frac{カイ2乗値}{N}} \end{aligned}\]ただこのPhiに関しては残業と離職の組み合わせのように2X2の場合はいいのですが、それ以上のカテゴリーの数がある場合には正確な値を求めることができないと言われています。そこでこのPhiを求める式に調整を入れたものがクラメールのVなのです。
クラメールのVは2つの変数のうちカテゴリーの数がより少ない方を選び、その変数のカテゴリーの数から1を引いものでカイ2乗値を割り、最後にルートをします。式にすると以下のようになります
\[\begin{aligned} クラメールのV = \sqrt{\frac{カイ2乗値}{N * (より少ない変数のカテゴリー数 - 1)}} \end{aligned}\]両者の値とも0から1の間をとり、0はまったく関連なし、1は完全に関連を意味し、大抵の場合はその間のどこかの値をとります。ガイダンスとして、以下のように解釈できます。
| 効果量 | 効果の大きさ |
|---|---|
| 0.1 | 小さな効果 |
| 0.3 | 中くらいの効果 |
| 0.5 | 大きな効果 |
2つのタイプのカイ2乗検定
実はカイ2乗検定には2つのタイプがあります。これまで見てきたのはカイ2乗検定の中でも独立性の検定と言われるものです。これは2つの変数に関係があるかそれともないかを検定するものです。上記の例では残業という変数と離職という変数の間に関係があるかどうかを調べました。
もう一つのカイ2乗検定は適合度の検定とよばれるもので英語ではGoodness of fitと呼ばれています。これは1つの変数のなかでのカテゴリーの比率が期待されているものと違うのかどうかを調べるものです。
ここでの期待値とはすでにわかっているものがあった場合です。例えば自分たちのビジネスの顧客の年齢層(10代、20代、30代など)のグループ比率が市場の一般的な年齢層の比率と同じようなものなのか、それとも違うのかを調べるといったものです。
この場合もカイ2乗値の計算の仕方は同じです。左側は実測値、右側は期待値となります。
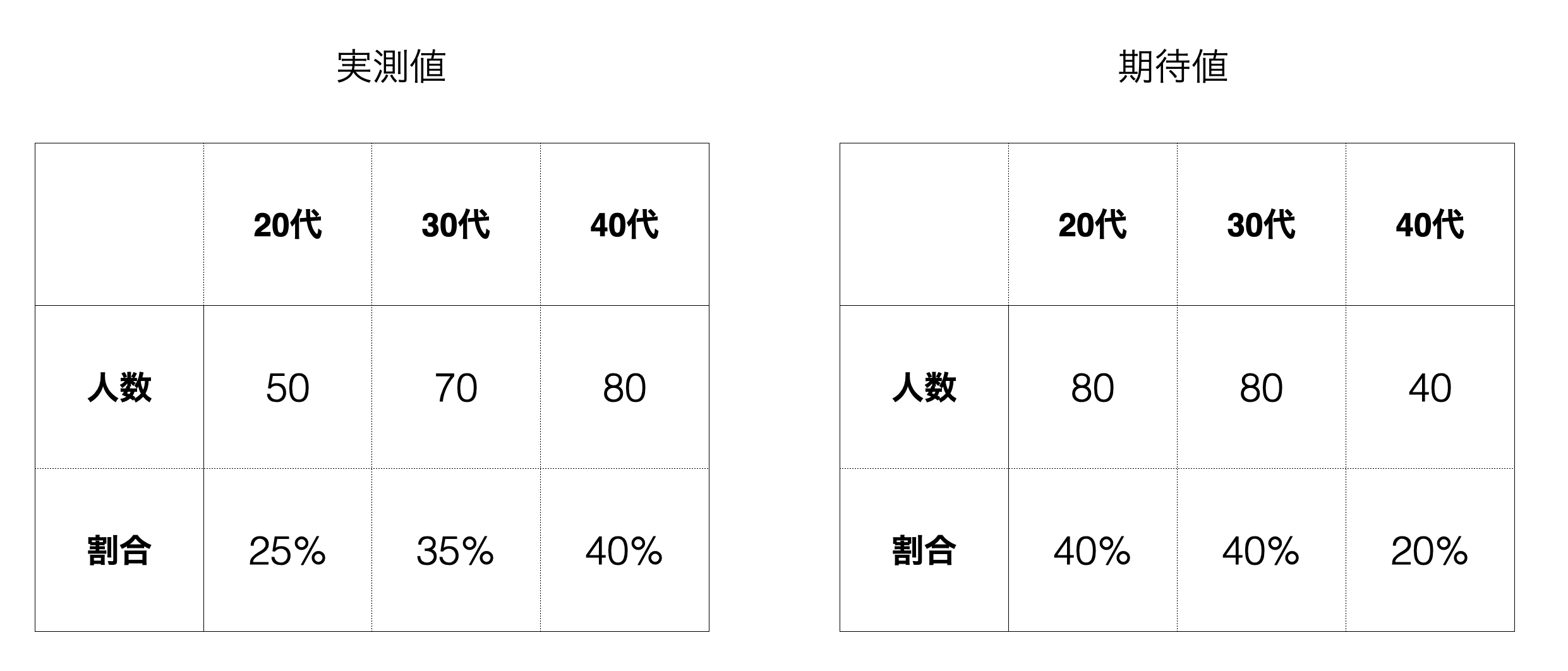
この場合それぞれの人数の実測と期待値の差を計算し、それを2乗したものを期待値で割り、それらを合計します。
例えば実測値の20代は50なので
\[\begin{aligned} \frac{(50-80)^2}{80} + \frac{(70-80)^2}{80} + \frac{(80-40)^2}{40} \end{aligned}\]次は自由度の計算です。この場合は3つのカテゴリーのため、3から1を引いて2となります。そこで自由度2のカイ2乗分布を使って上記のカイ2乗値かそれ以上に大きい値が得られる確率を求めます。