第8章 仮説検定
これまで、推測統計における2つの大きな枠組みのうち,推定というものの背後にある考え方について説明してきました。この章ではもう1つの枠組みである仮説検定について考えてみたいと思います。
仮説検定とは、母集団に関する仮説が正しいかどうかを、手元にあるデータと確率論を使って検証するための統計学的手法です。これは科学的思考の章で話したことを思い出してみてください。「私たちが正しいと思っていることをどうすれば正しいとわかるのでしょう。」この質問に答えるために大きく二つの考え方があるという話をしました。1つは演繹法とういうものですが、それは一般的に正しいと受け入れられている前提からスタートして論理的に正しい答えを求めるというものです。しかし、この考え方には落とし穴があります。というのはその前提が間違っているかもしれないということです。
そこで帰納法では実際に現実世界で起きていることを観察し、そこから十分な証拠を集めた上で一般的にも通用する答えを求めようとするものです。この演繹法とから帰納法の両方を使って、私たちが興味の対象に対して持つ仮説を演繹法におけるところの前提としたときに、そこから論理的または理論的に正しいと思われる結論と、現実世界で起きている現象が辻褄があっているのかどうかを検証するのが仮説検定です。
ただこのための続きや、実際に行なっていく際の考え方が、初めての人にとっては少しややこしいもので、統計学の授業でもこの仮説検定の考え方や出てくる専門用語で多くの人が混乱する場所です。しかし、この仮説検定の考え方や使い方を理解するためには特に高度な数学的な知識が必要というわけではありませんし、一度慣れてしまうとそんなに複雑なものでもありません。
そこでまず、仮説検定における考え方についてしっかりと説明し、その後に仮説検定を行うにあたっての基本的な手続き、解釈の仕方などについて解説していきたいと思います。
演繹と帰納
アメリカに住んでいると、友達の家などで大きなパーティが開かれることが多いのですが、そういったときに必ず「俺はワインに詳しい」という人が出てきます。私もワインは大好きなのでそういう人がいればワインについて話したりするわけですが、こういうときにかなり強気に主張してくる人がいます。
実際ある晩、フレデリックという若い男性が「フランスワインとカリフォルニアワインは全然違うので、飲めばすぐにわかる」と言いはじめました。まあ実際この2つの国または地域から出てきたワインには結構違いがあったりするものですし、ソムリエのような人であれば実際こうした違いには敏感なのかもしれません。
フランスからやってきたフレデリックはフレンチワインはカリフォルニアワインとは決定的に味が違うと主張します。彼に言わせるとフレンチワインにはテロワールがあるので、あじに深みがあると。
その場にいるみんなも、彼のフレンチ訛りの英語のアクセントと、彼がフランスから来たということで、なるほど彼はワインのことを知っているのだろう、そして彼がそういうのだからフレンチワインとカリフォルニアワインには決定的に違うのだろうと。
そこで例の科学的手法を思い出してみてください。
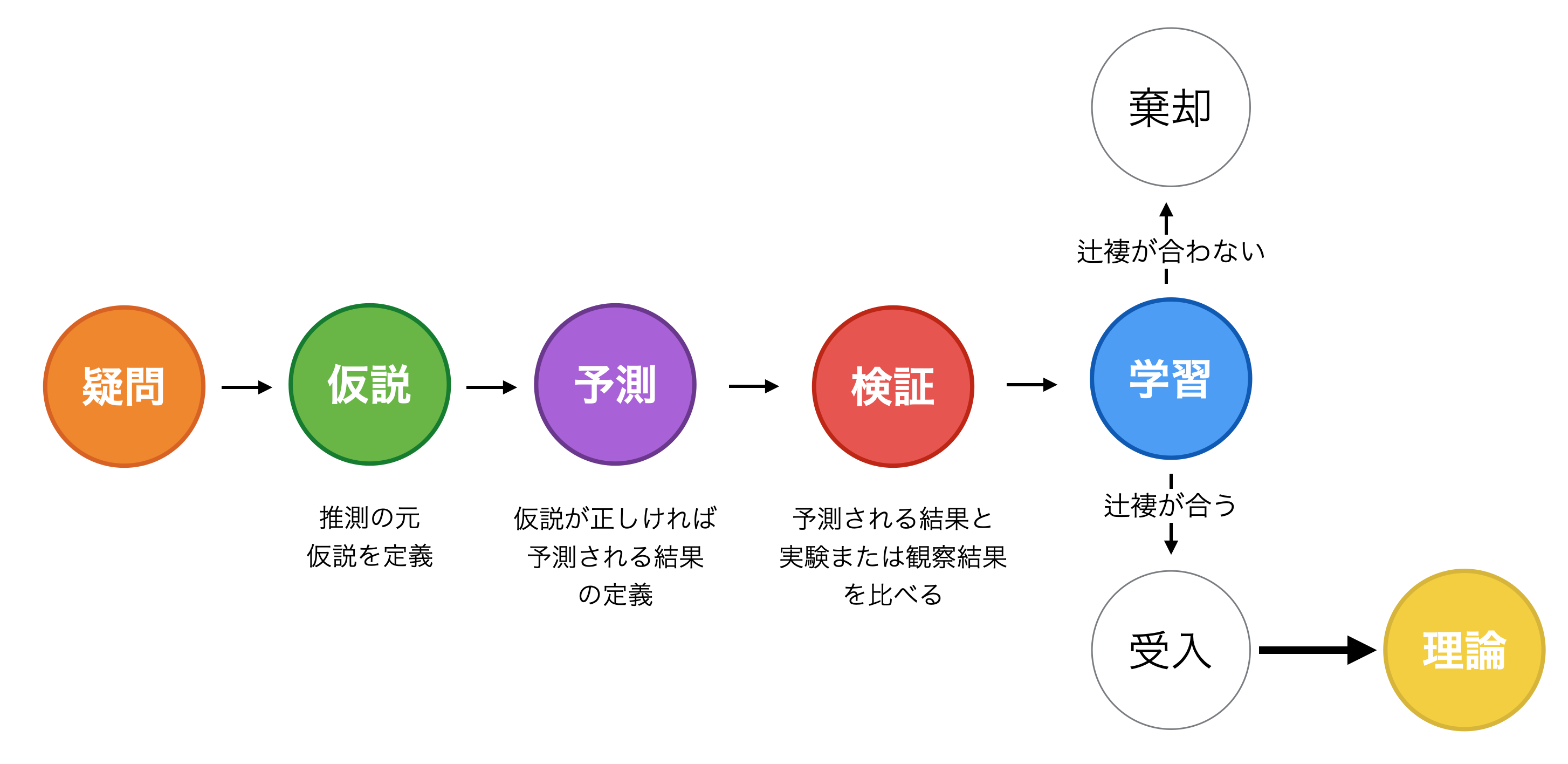
今ここで疑問となっているのは「フレデリックはフレンチワインとカリフォルニアワインの違いがわかる」のかどうかです。
そこで一つの仮説が出てきました。
彼はフランス出身で、これまでワインをよく飲んできたのでフレンチワインに詳しい。そのため、フレンチワインとカリフォルニアワインの違いがわかる。
そしてこの仮説が正しいのであれば、「フレデリックはフレンチワインとカリフォルニアワインの違いがわかる」と予測できます。
ここまでは演繹的な考え方です。論理的には筋が通っていそうで、納得できるものでもあります。
しかし、だらかといってフレデリックが実際フランスワインとカリフォルニアワインとの違いがわかるかどうかは別の話です。このどっから出てきたかもわかならい、今日初めて会った人が、本当にワインにくわしく、この2つのタイプのワインの味を見極めることができるという保証はどこにもありません。そもそも彼がフレンチワインをよく飲んでいたというのはほんとうでしょうか?最近はフランでは特に若い人はワインをあまり飲まないという話を聞いたことがあります。また同じフランスでも地域によって違いもあるかもしれません。そもそも彼がほんとうにフランス人だというのはほんとうでしょうか?お隣にベルギーという国がありますが、ここではフランス語を話しますが、ワインの生産よりもビールの生産、消費で有名なお国です。実はフレデリックはベルギー人だったなんてことはないのでしょうか。
もしそうならなぜこんな主張をするのかって?それは独身の彼は女性の多いこのパーティで、見栄を張りたいからではないでしょうか?ワインに詳しい人が女性に人気があるのかどうか知りませんが、単純な男性は女性の前ではなんでもいいから競争的になるものです。
なーんてことを疑い深く考える人たちの頭ではどうも納得がいきません。
するとそんな納得のいかない私たちを見計らったかのように、急にシリコンバレーのテック企業で働くクリスが、「じゃあ、テストしてみればいいじゃん!」と言い出しました。フェイスブックやネットフリックスといったシリコンバレーのテック企業では、長々と議論するよりも、さっさと実験してみればいいじゃないかという文化があります。そしてこれこそが、科学的手法です。
理屈がほんとうに正しいのかどうかは、現実世界で実際に試してみればいいのです。これこそが帰納的な考え方です。
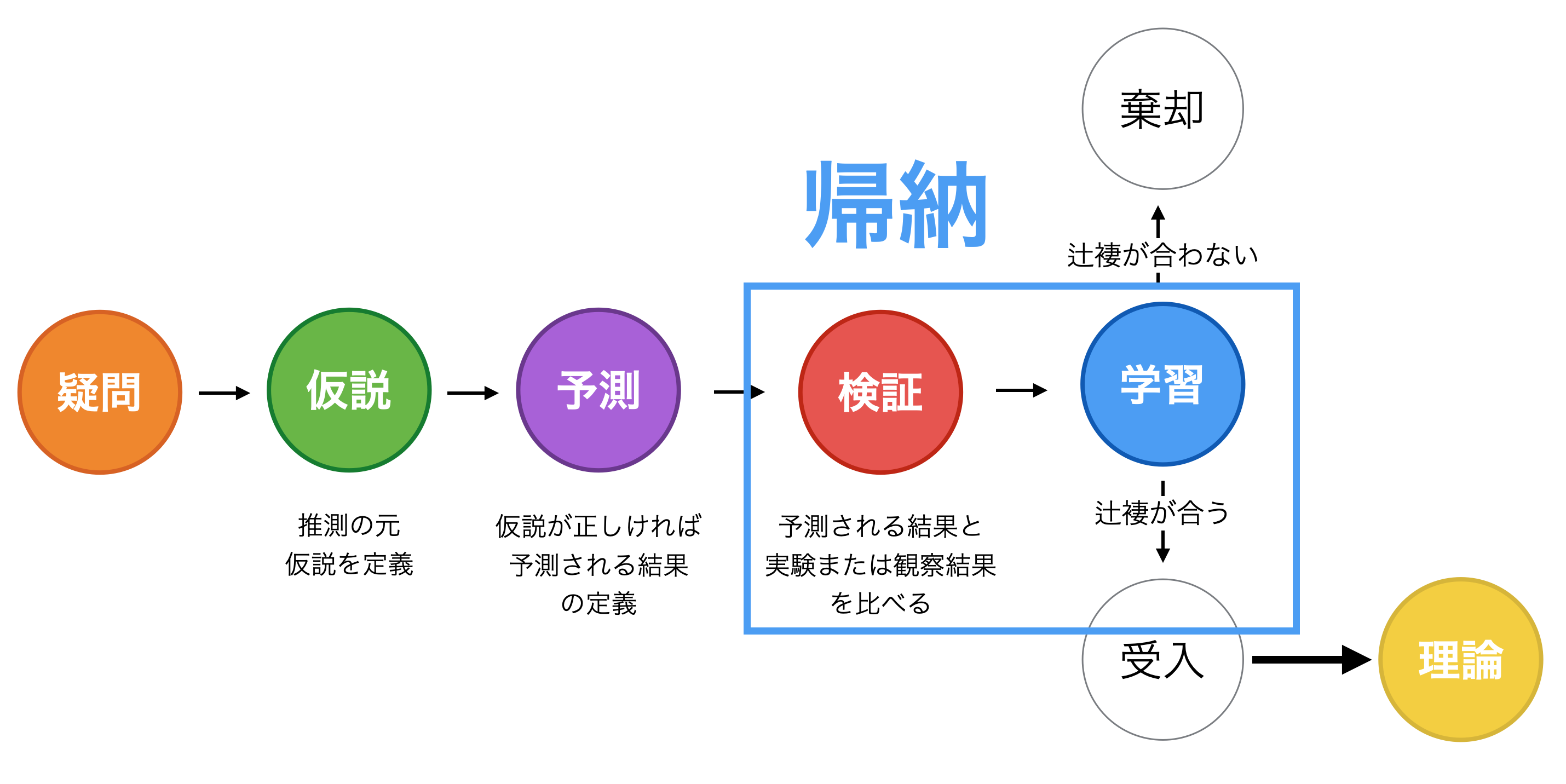
科学的思考の話を思い出してください。ガリレオ・ガリレイの時代まで理論だけで地球が中心で他の惑星や太陽はその周りを回っているという説を受け入れていました。そこではどんなに太陽が中心であるという説を説明してもそれまでの一般的に受け入れられている説を覆すことができなかったのです。そこでガリレオが行ったのは現実の世界で起きていることを観察し、理論との整合性を検証するというものでした。つまり帰納的に真実を追求するということでした。
実験
それではどうテスト(実験)するかということなのですか、ワインの世界ではよく行われるのですがブラインドテイスティングを行うことにしました。ブラインドテイスティングとは、ワインを試飲する人はラベルも何もないグラスに注がれたワインを飲み、そのワインについて評価したり、またはそのワインが何なのかを当てるというものです。
さすがに一杯だけ用意して、その一杯を当てることができるかどうかというのもどうかと思います。この世の中のデータはばらつくわけですから、人間だって多少ばらつきます。どんなに頭のいい人だってテストに完全に答えることはできません。
そこで今回はカリフォルニアワインとフレンチワインを5本ずつ用意し、それぞれをラベルも何もないワイングラスに注ぎ、それらをランダムにシャッフルした上でフレデリックの目の前に出し、一つづつカリフォルニアかフレンチかを当ててもらうというものです。

一杯ずつ飲んではどちらの地域のワインだと思うかを発表し、最後の10杯目まで行うわけですが、それぞれのグラスを飲み干す必要はありません。少し口に含む程度の試飲で見極めるので、最後の方になってくると酔っ払って判断力が鈍るということはほぼないというのが前提です。実際にはフレデリックは試飲にしては多い量を飲んでいましたが。
何はともあれ、テストの方はフレデリックが酔っ払って倒れることなく、無事に終わり、答え合わせをしたデータも集まりました。すると以下のようにフレデリックは10杯中7杯で答えが合っていました。
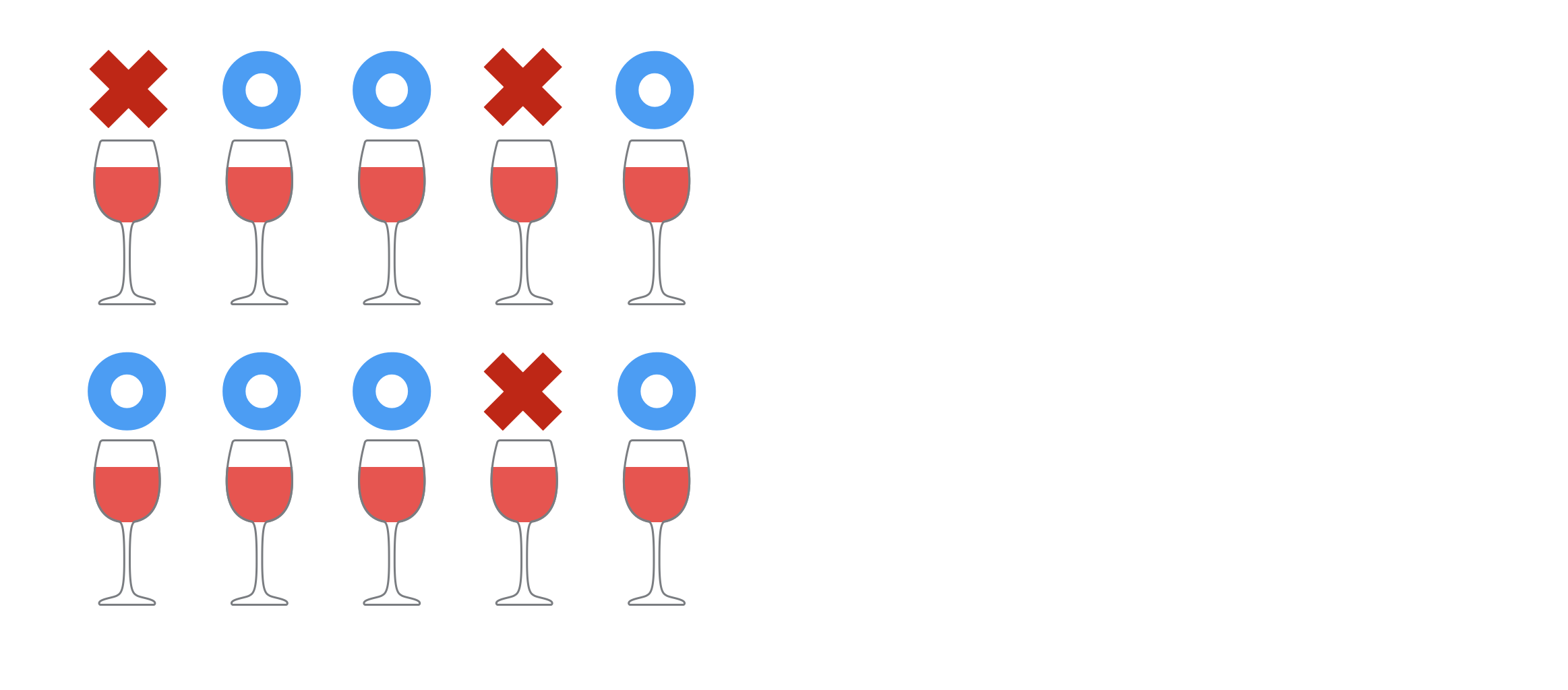
口だけでなく、現実世界で実験をし、データをとったわけですからこれで議論は終結するだろうと思ったところ、ここで新たな議論が「フレデリックはワインの違いがわかる」派と「いや、適当に言っててたまたまあたったんだよ」派に分かれて始まりました。
「ワインの違いがわかる」派は、「間違いもあるけど、7割の答えが合ってたんだから何か知ってるってことでしょう。」と主張します。
それに対して「適当に言ってるんだよ」派は、「ほんとに知ってたらもっと当たってるわずでしょう。7割なんて、100点満点のテストで言えば70点でしょ。そんなんじゃ落第でしょう。」と言い出す始末です。
さて困ってしまいました。せっかく実験をしてデータを集めたにも関わらず、議論は収まるどころか逆に収集がつかなくなってしまいました。
どうすればよいのでしょうか。
反証できる仮説としての帰無仮説
今回は70%の正答率だっため、中途半端な形になりましたが、それでは仮にもっとわかりやすい結果だったらどうでしょうか。
例えば80%、つまり10杯中8杯当たっていたらどうでしょう。
この場合、フレデリックを支持する人たちはほら見たことかと勝ち誇るでしょう。しかし、反対派は2杯も外してしまったことを取り上げて、フレデリックはやっぱりわかってないではないか、適当に言ってるだけだというかもしれません。
逆に今度は10杯中6杯しか当たってなかったらどうでしょうか。反対派は、このときこそフレデリックは適当に言ってるだけで全然わかってないということでしょう。しかし、フレデリック支持派は「半分以上当てることができたんだから彼はやはりワインの違いがわかる人だ」と言うかもしれません。
どんな結果になったとしても「フレデリックはワインの違いがわかる」という説を主張し続けることができます。ここで問題になっているのは、現在持っている仮説は反証が不可能だということです。こういう事実やデータが提示されたら、その仮説が間違っていたと認めようという基準が事前に決められていなかったため、せっかくテストを行ったにも関わらず、さまざまな言い訳、または正当化するための議論が特になんの根拠もなく好き勝手に行われてしまったということです。
これはビジネスの現場でもほんとによくあることです。サインアップ率を上げるために何か新しい施策を行い、そのさいデータを見よう!ということになりデータを集め、サインアップ率が上がったかどうかを見たりするものです。しかし、ここで上がってなかったとしましょう。すると、この施策の責任者は打たなかったらもっと悪かっただろうと言い始めます。逆に、サイト訪問者の数が増えているのだからいいではないか、と言い始める始末です。
このようにデータを使っても、反証できる仮説を定義できてなければ、いつまでたっても意見を変えることができなくなってしまうのです。一般的には、コロコロと意見を変える人を朝令暮改などといって、ネガティブに捉えられがちです。しかし、重要なのは何が真実なのかを見極め、より曇りのない天候の中でターゲットに向けて飛んでいくことです。そのためには、間違った方向に向かって飛んでいたのであれば、さっさと方向転換をしなければいけません。つまり必要であれば意見を変えると言うことです。
もちろん、なんの根拠もなく言われたまま意見を変えるのも問題です。しかしいつまでたっても意見を変えることができないのであれば、それは宗教と変わりません。何があっても信じ続けると言うものです。信仰に関してはそれはそれで重要なのですが、科学の世界は信仰の世界とは違います。これはどちらが正しいとか、良いとか言おうとしているのではありません。これら2つは別のものだということです。
そして統計学とは科学の世界のもので、データサイエンスと言われるものも、もちろん科学(サイエンス)の世界のものです。
それでは反証できる仮説とはどういうことでしょうか。
これは実はシンプルで、元の仮説を反対にして、「違いがわからない」としてしまえばいいのです。というのも、これによって「フレデリックは適当に言っている」と仮定することができます。適当に言っているのだとすると、それはコインを投げて表か裏かを当てるのと同じようなものだと言うことです。つまり確率的に50%で当てることができるだろうと言うことです。
「違いがわかる」という仮説だと、何を元に違いがわかるのかがあいまいでした。90%であればよいのか、70%であればよいのか、基準がありませんでしたし、無理に例えば80%などと基準値を設けようとしても、それ自体がまた新たな議論を巻き起こすことでしょう。
しかし「違いがわからない」としたことによって、当たる確率は50%としてしまえば、この数字に対して異論を差し込む人はいないでしょう。もちろん、確率論の章でも見たように、理論的には50%でも実世界ではばらつきます。そこでこのばらつきも考慮しなくてはいけません。しかし、この理論的には50%だというときの50%という数値はだれもが納得できるもののはずです。
このような「違いがない」といったような関係が無いとするような仮説のことを帰無仮説と呼びます。「無いに帰する」ということで帰無仮説というわけですが、この言葉はこの先も仮説検定をする限りは何回も出てきます。
今回の場合は元々検証したかった仮説は「違いがわかる」でした。しかし、この仮説はこのままでは反証できません。反証するための基準がないからです。そこで反証できるための仮説にするために逆転させ「違いがわからない」としたのでした。これによって明確な基準ができました。
仮説:違いがわからない
予測:5割当てることができるだろう
確率分布
ところが、理論的には50%でも現実世界でそうなるとは限りません。現実世界ではデータはばらつくものです。つまりフレデリックがたとえ適当に言っていたとしても、コイン投げと同じで、10回あれば7回当たることもあれば、9回当たることもあるのです。ただ、確率論のところで話したようで、それでも何回もやっていれば5回当たる確率の方がより高く、その確率は7回よりも高く、7回当たる確率の方が9回よりも高いはずです。
<確立分布>
そこで、例えば7回当たったとした時に、「適当に言ってたとしても7回当たることもある」ではなく、「適当に言ってたとしたら7回当たる確率はX%だ」と話せるようになればいいのではないでしょうか。
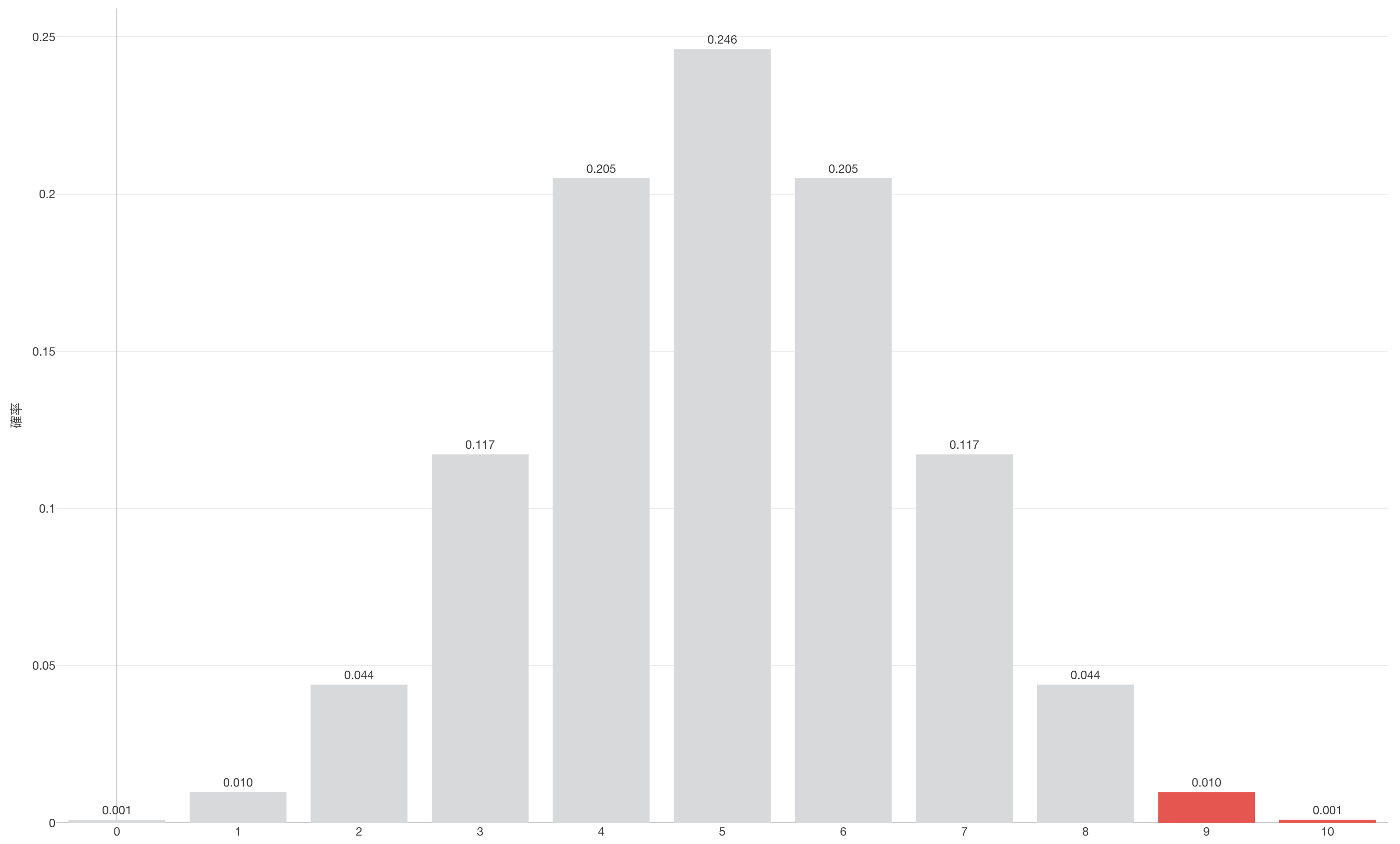
そこで、今回のように「当たる」と「外す」というように2つの結果しか取らないような場合の確立分布ということで、二項分布を使うと、それぞれの当たった回数に対しての確率を出すことができます。
<確立分布>
そこで、例えば9杯当たったとしましょう。すると適当に言っていたとして9杯当たる確率は1%ほど(0.01 + 0.001)です。1%くらいでしか起きないということはほぼ起きえないと言うことですよね。つまり、この「適当に言っている」と言う仮説を前提としたモデルでは、この目の前に起きている現象は想定外ということです。つまりこのモデルでは説明できないと言うことになります。つまり理論的に導き出された世界と、現実の世界では辻褄が合っていないと言うことです。
<モデルとデータの箱と線を描いた絵を描く>
逆に6杯当たったとしましょう。すると適当に言っていたとして6杯以上当たる確率は約38%ほど(0.377)です。約38%の確率で6以上当たるよと言われて、実際に6杯だったのであれば、ここで使っているモデルは信用できそうです。当たったくらいであればよく起きそうです。つまり「適当に言っている」と言う仮説を前提としたモデルでも、この目の前に起きている現象は特に想定外というわけではありません。つまりこのモデルで説明できるということになるのです。つまり理論的に導き出された世界と、現実の世界では辻褄が合っていると言うことです。
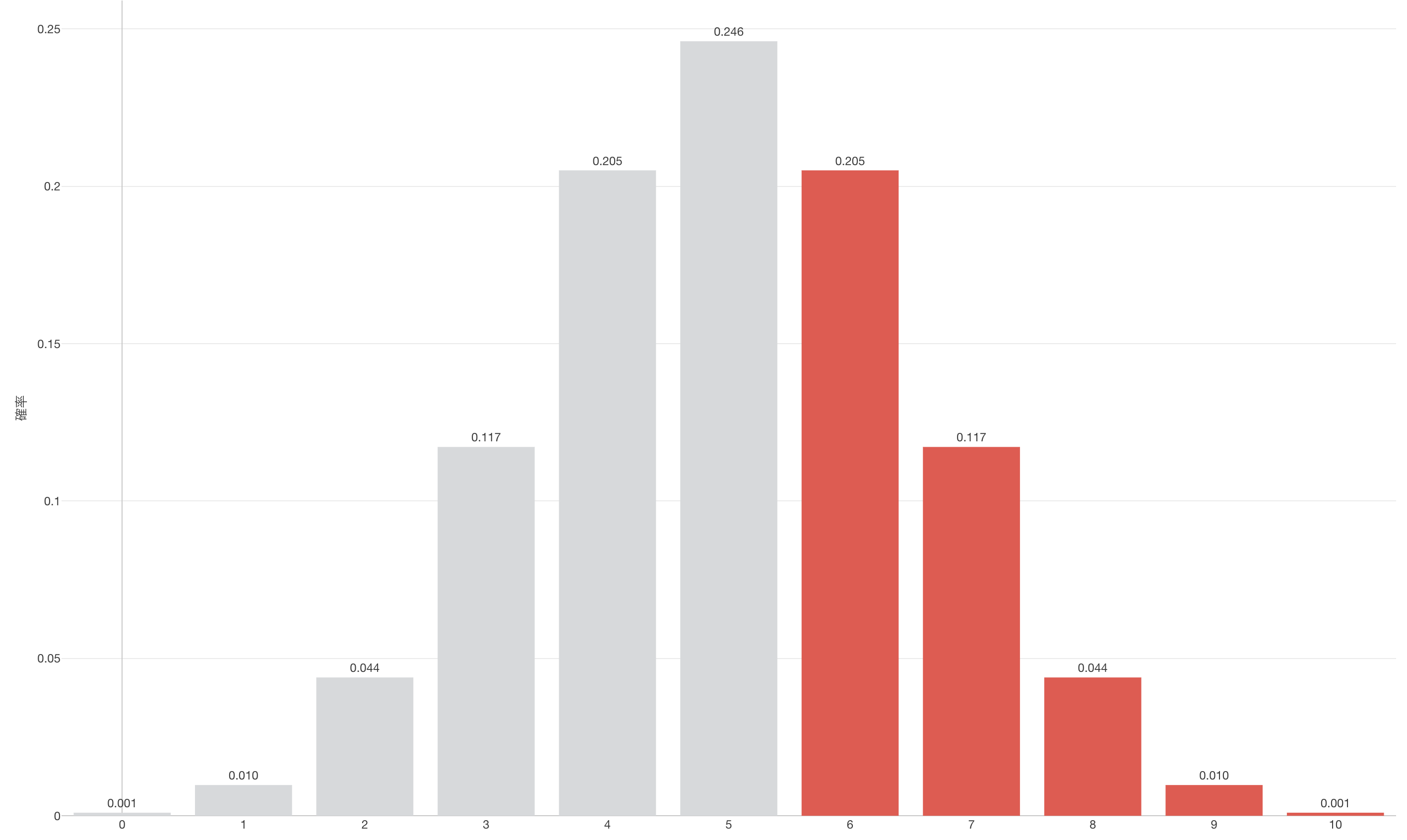
<理論と現実が辻褄が合っている>
P値
もし帰無仮説である「違いがわからないので適当に言っている」が正しいとしたときに、実際に10杯中9杯以上当たる確率は約1%ほどでした。さらに、10杯中6杯以上当たる確率は約38%でした。
実はこうした確率のことを統計学の世界ではP値と呼びます。PはProbabilityの頭文字で、Probabilityは日本語で確率という意味です。ですがこのP値はただの確率ではありません。帰無仮説が正しいと受け入れた場合に、目の前に起きている現象が起きる確率です。今回の実験ではフレデリックにはワインの違いがわからない、つまり適当に言っているというのが帰無仮説です。適当に言っているのであれば理論的には50%の確率、2回に1回、10回に5回当たるということです。それでも現実世界ではデータはばらつくため、10回に9回当たることもあれば、6回当たることもある。じゃあ、そう言った結果が出る確率は?この確率がP値です。
ここで注意が必要なのは、10回中9回当たったとした場合、そこで問題となる確率はちょうど9回当たる確率ではありません。9回以上当たる確率となります。つまり9回当たる確率と10回当たる確立の合計です。もし10回中6回当たった場合、6回以上当たる確率が38%です。
というのも、ここで判断したいのは帰無仮説を前提とした確率分布というモデルの世界ではどれだけ珍しいことが起きているのか、それとも当たり前のことが起きているのかです。ですので10回中9回当たったという場合、9回でも10回でも、9回以上当たると言うことがそもそも珍しいことなのかどうかを判断したいのです。
そして同じように10回中6回当たると言う場合でも、6回でも7回でも8回でも、6回以上当たると言うことがどれくらい珍しいのかと言うことです。
つまりP値とは帰無仮説を前提とした確率分布を使うと、目の前に得られた値かそれよりももっと珍しいであろう結果が起きうる確率ということになります。
さてここで問題です。
もしフレデリックが10回中7回当てていたとするとどうなるでしょうか。その場合のP値は17%ほど(0.172%)です。 7回以上当たる確率ということで、7回、8回、9回、そして10回の確率を足し上げたものです。さて、この17%という数値をどう捉えれば良いでしょうか。これは想定外と呼べるほど珍しいことが起きていることを示しているのでしょうか?それとも起きても別にそんなに不思議でも無いよね、と気にせずにいられるレベルでしょうか?
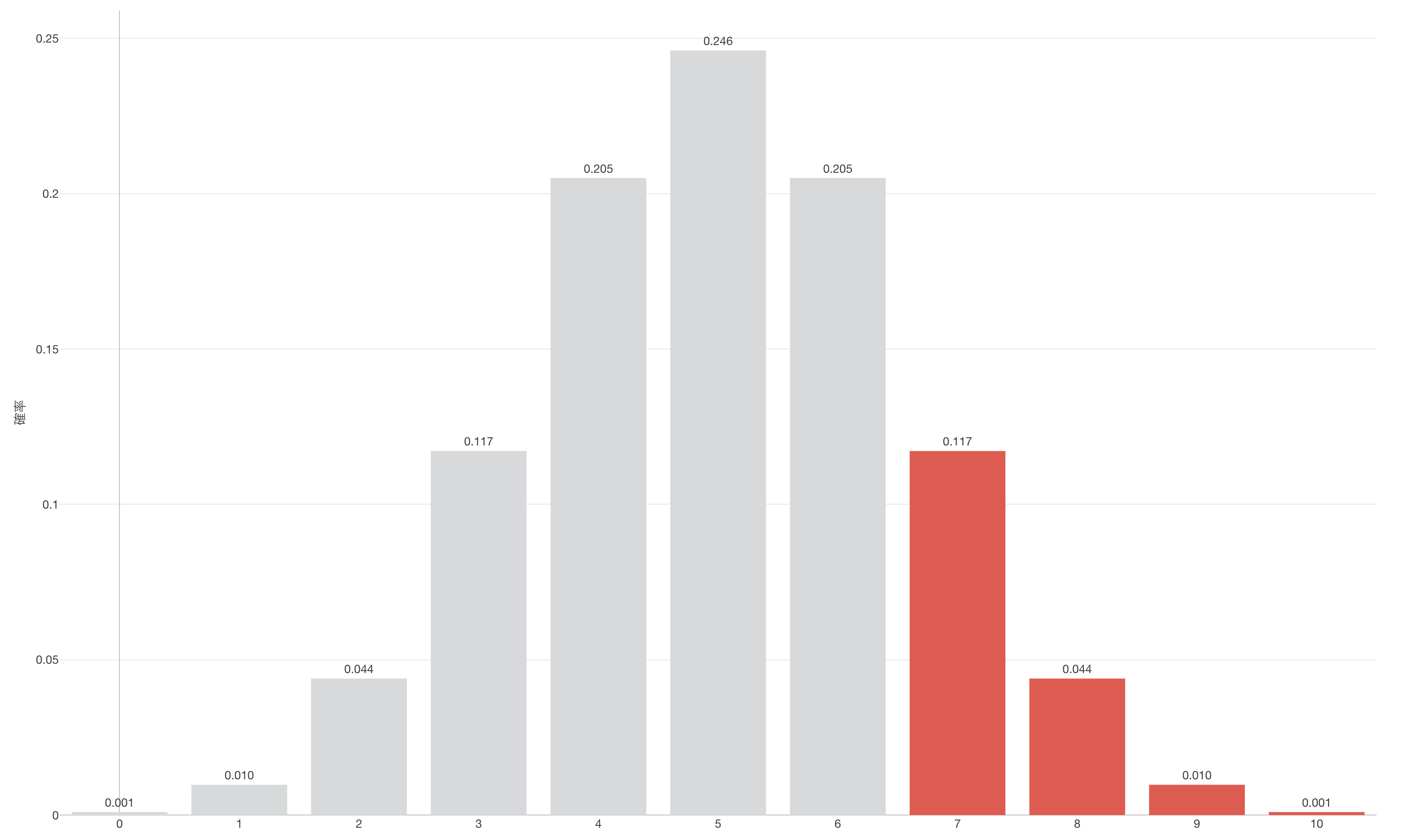
ここで問題となっているのは、何%未満だったら前提としているモデルの世界では「あり得ない」と言えて、逆に何%以上であれば「あり得る」と言えるのかということです。実はこれに関して何か客観的で、誰もが納得するような水準があるというわけではないのです。一般的には、昔からよく5%という数値がよく使われているとしかいいようがない数値しかありません。そして、もしP値が5%未満であれば、それはここでのモデル(この人は適当に言っている、つまり二項分布の確率分布に従う結果を出すというモデル)では想定外のことが起きている、つまり説明できない。なので元となる仮説を棄却するということになります。
逆にもしP値が5%以上なのであれば、このモデルを使っても想定外のことが起きているわけでははい、つまり説明できる現象が起きているということで、モデルの元となる仮説、つまり「適当に言っている」という仮説を支持し続けることとなるのです。
5%がもっとも有名な数値なのですが、他にも1%だったり、0.1%だったりと言った数値が使われることもあります。科学の世界でも分野によってこの水準となる数値に違いがあったり、さらにビジネスの世界でもこの数値はもっと大きく10%、20%なんてこともあります。
ただここで何%であることが最も正しいのかと議論してもあまり意味がありません。というのもここで私たちが知りたいのは、どれだけ珍しいことが起きているのかということです。そしてこの水準とは業界や分野、さらにはデータによって異なってくるものなのです。そこで、最終的には自分たちの観察対象、データによってどれくらいの数値が最適なのかを経験値的に探していくということが求められます。
何を基準に探せば良いのかというと、それは有意であると判断した場合に間違ってなかったかどうかということです。例えば5%という有意水準を採用した場合にP値が3%だった場合、それは有意ということになりますが、その判断を下し何か行動をとってみたが、あとで時間を置いてみると特に違いがあるというわけではなかったのであれば、5%という水準は違いが有意であるというには優しすぎたということかもしれません。そこで、もう少しこの水準値を厳しめに設定してみればよいのです。例えば1%という具合にです。
その逆もそうです。得られたP値が8%だったため有意でないと判断し、特に何も変更せずにビジネスを進めていたのだが、しばらくすると実は違いがあったと観察されたのであれば、5%という水準は厳しすぎたのかもしれません。その場合は例えば10%、15%といった具合に水準値を上げることによって、有意にしやすくしてやればいいのです。
ただそれでも、いきなり仮説検定をやったこともない人に、自分で最適な数値を見つけてくださいといっても混乱するだけです。そこでこの5%といった広く一般的に使われている水準値からスタートしてみるのがいいということです。
ところで、1つ気をつけなければいけないのは、この水準値を決めるのは後出しジャンケンになってしまってはいけないということです。というのは私たち人間は誘惑に弱いですから、結果が出てから水準値を決めることを許してしまうと、自分に都合の良いように決めてしまうことになりがちです。有意としたければ、水準値を上げるだろうし、したくないのであれば水準値を下げるでしょう。
これではさすがに客観性もなければ、他の人が同じような実験をした場合でも同じ結果になることを保証する再現性もなくなり、誰からも信用されないあやしい実験となってしまいます。そこで水準値がなんであれ、その値は実験を行う前、データを見る前に決めておく必要があります。
そこで、この本では5%を仮説検定における水準値として採用します。
先ほどのケースで言えば、もし10杯中9杯当たっていた場合は、その場合のP値は約1.1%、水準値である5%よりも小さい数値なので、起きえないことが起きているということです。つまり、帰無仮説である「適当に言っている」を元にしたモデル(二項分布)のモデルの(理論の世界)と実際に起きている現象(現実の世界)は矛盾しているということですので、帰無仮説である「違いがわからない、適当に言っている」を棄却することになります。
ここで重要なのは、期待、または予測された結果と現実世界での結果が辻褄が合っていないのであれば、その予測を作る元となった仮説を棄却するということです。
しかし、もし10杯中6杯しか当たっていなかった場合は、その場合のP値は約38%、水準値である5%よりも大きい数値なので、起き得ることが起きているということです。つまり、帰無仮説である「適当に言っている」を元にしたモデル(理論の世界)と実際に起きている現象(現実の世界)は辻褄が合っているということですので、帰無仮説である「違いがわからない、適当に言っている」を棄却する必要はありません。むしろ受け入れ続けることになります。
4.2 統計的に「有意」であるということ
統計も占い他のオカルト技法と同じだ。内輪でしか通じない専門用語を意図的に多用し,門外漢にはその方法がよくわからないようになっている。
- G・O・アシュリー
ここで「有意」という言葉について少し考えてみましょう。
統計的有意性の概念は実際にはとても単純なのですが,この名前のせいでよく混乱が生じます。データによって帰無仮説が棄却される場合,私たちは「この結果は統計的に有意だ」と言います。もう少し短く「結果が有意だ」と言うこともあります。
この「有意」英語では「significant」と呼ばれる統計用語はかなり古い歴史を持っています。もともと英語の「significant」は「示された」というような意味を持っているのですが、現在では「重要である」にといった意味で用いられることが多くなっています。
その結果、統計学を学ぶ人々の間で多く混乱が生じることになってしまいました。なぜなら「有意な結果」というとそれがあたかも重要なものであるかのような印象を与えてしまうからです。しかしそのような意味は一切ありません。
「統計的に有意」という言葉は「データによって帰無仮説が棄却される」というだけの意味で、それ以上でもそれ以下でもありません。その結果が現実世界において重要かどうかというのはまったく別の問題で、それを測るためのものではありません。
もう一つのP値の解釈の仕方
極端な値の出現確率
P値の解釈の仕方には実は2つあります。1つはこれまでみてきたものです。
それはある帰無仮説を前提にした時、得られた値かそれよりも起こりにくい値が得られる確率としてのP値でした。そして、もし有意水準を5%と決めていたのであれば、このP値が5%よりも小さければ帰無仮説を棄却することができ、有意である、つまりその値はキム仮説では説明できないほどに大きい、または小さいということにになります。
この考え方はロナルド・フィッシャーによって提示されたためフィッシャー流の解釈と言われるものです。たいていの統計学の教科書ではこの解釈がとられています。
ここではもう1つの解釈の仕方、それはイェジ・ネイマンという統計学者によって提示されたものを紹介します。先に言っておくと、どちらが正しいというわけではなく、どちらも正しいものです。しかしどちらも最初からしっかりと理解できてないといけないわけではありません。まずは自分が解釈しやすい方を使えば良いと思います。
結果の判断に対するより柔軟な考え方
これまでに見てきたフィッシャー流のP値の解釈の仕方に対して1つ問題を挙げるとすれば、「かろうじて有意」な場合と「明らかに有意」な場合の区別がまったくないというものです。たとえば、もう一度ワインテイスティングのテストで10杯中8杯当たっときのことを考えてみましょう。その場合のP値は5.5%となります。
0.044 + 0.01 + 0.001 = 0.055 (5.5%)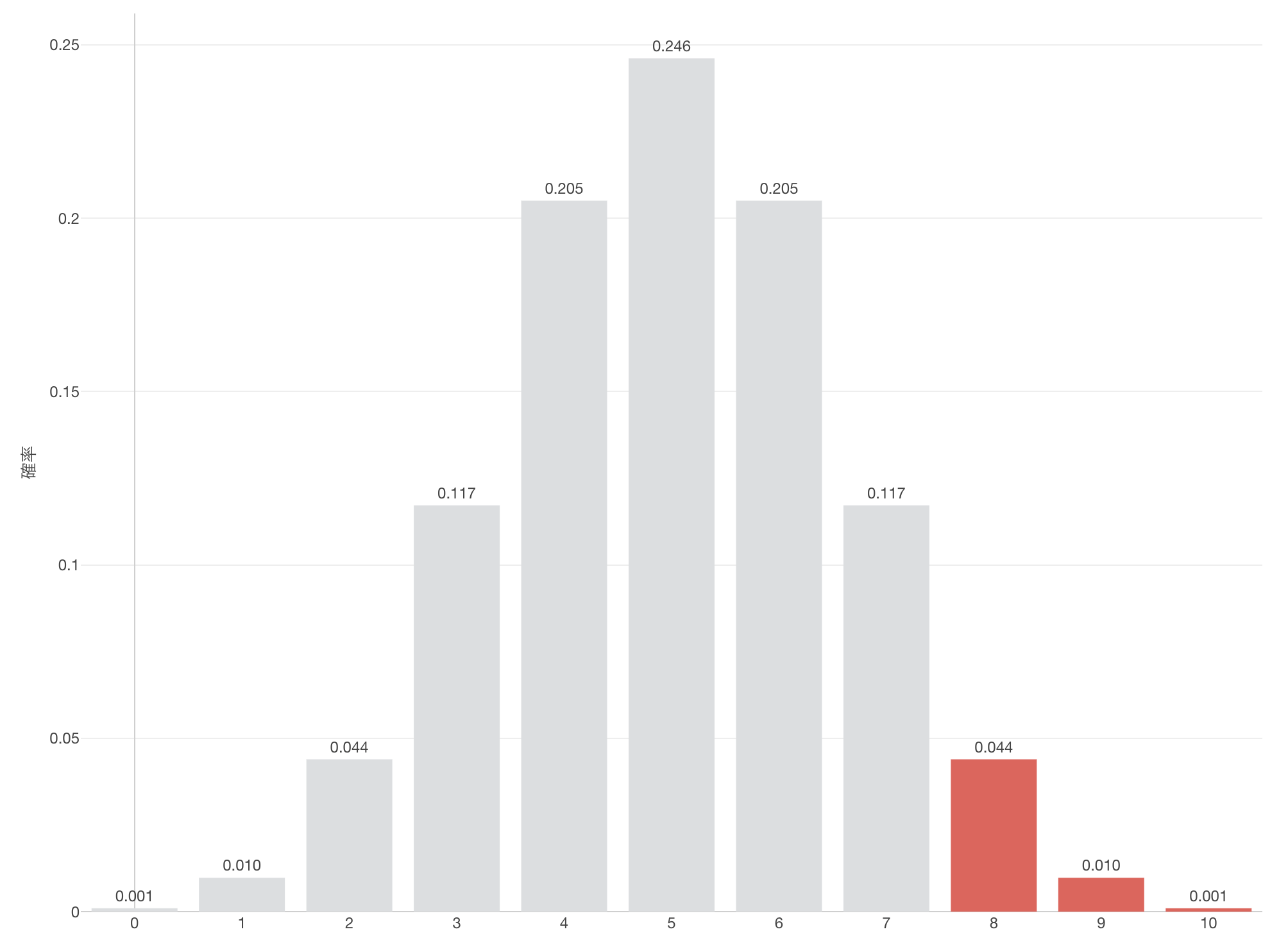
すると有意水準を5%にしていたのであれば、結果は有意でないということになります。つまり5.5%は5%より大きいのですから、帰無仮説を前提としていたとしても、あり得ることが起きているということです。しかし、これはかなりギリギリの範囲です。あと少しP値の値が小さければ、例えば4.9%であれば有意になっていたのです。
逆にもっとP値の値が大きかった場合はどうでしょうか。例えば10杯中6杯当たっていた場合は、P値は38%でした。この場合有意水準である5%に比べて大きいため、有意でないということになるのですが、さきほどの5.5%の場合と比べて起き得る確率はかなり高いと言えるでしょう。
逆に有意であるというケースも考えてみましょう。例えばもしP値が4.7%の場合と0.1%の場合を考えてみましょう。どちらも有意水準である5%に比べて小さいため、有意であるということになりますが、これらの数値には大きな違いがあります。4.7%、つまり約5%ほどであれば人によっては、それは起き得ると捉える人もいるかもしれまえん。しかし、0.1%であれば、ほとんどの人がそれはあり得ない確率だと思うでしょう。
しかし、仮説検定を行い結果を出した際にはどちらのケースも有意となるのです。そこにはなんのニュアンスもありません。ぎりぎり有意となった、余裕で有意だったという差はないのです。
5.5%であれば有意でないという判断をし、4.7%であれば有意であるという判断をするとき、こうした判断というはどれくらい信用できるのでしょうか。そもそもデータはばらつくわけですから、ちょっとでもデータが増えたり減ったりすることによって、これくらいの確率であれば上がったり下がったりすることもあるのではないでしょうか。
そしてそうしたばらつきによって、5.5%というP値が4.9%に変わってしまったり、4.7%が5.1%に変わってしまったりすることもあるのではないでしょうか。つまり、仮設検定をし、有意である、有意でないという判断を下したとき、そうした判断が間違っているという可能性があるのではないかということです。
ここで仮説検定における間違いが起きる可能性について考えてみましょう。
仮説検定における2種類の誤り
仮説検定をしなんらかの判断をした際には2つのタイプの間違いが起きる可能性があります。1つは有意だと判断したが、実は有意でなかった場合です。図にすると以下のようになります。

有意であると判断したが実は有意でないという場合の間違いをタイプ1エラーまたは第一種過誤と呼びます。これはワインテイスティングの例で言うと、フレデリックはワインの違いがわかると判断したのですが、実は彼は違いがわからずただ適当に言っていたと言う場合です。
逆に、有意でないと判断したが実は有意であったと言う場合の間違いをタイプ2エラーばまたは第二種過誤と呼びます。ワインテイスティングの例で言うと、フレデリックはワインの違いがわからないと判断したのですが、実は違いがわかっていたという場合です。違いがわかるのですがたまたま今回のテストではうまく答えられなかったということですね。
実はこのタイプ1エラーが起こり得る確率というのがP値なのです。P値の有意水準の話を思い出してください。有意水準を5%に決めた時、私たちは5%未満であればほぼ起き得ないよね、と暗黙のうちに合意していたことになります。しかし、それは絶対に起き得ないと言っているわけではありません。確率ですから、例えば100回あれば5回は起きることもある、これが5%の確率ということです。ですので、5%を有意水準にするというのは私たちが有意であると判断した時に5%の確率で間違ってるかもしれないということを受け入れているということにもなります。
そこでもし、いや私はそんな高い確率で間違いを受け入れたくないというのであれば、この有意水準を低くすることもできるわけです。例えば1%にしたのであれば、それはもし有意だと判断した場合に1%の確率で間違っているかもしれないがそれくらいであれば受け入れることができるとしたことになります。
そしてこれをさらに発展させると、もしP値が3%の場合に有意だと判断したのであれば、有意水準が5%なのか10%なのかに関わらず、それはこの判断を下した場合に間違っている可能性は3%だが、それを受け入れたということになります。もしこの3%で間違っているかもしれないという事実があなたにとってイコゴチが悪いというのであれば、有意であると判断しなければいいのです。逆にP値が10%で有意だと判断した場合、その判断が間違っている確率が10%であるという事実を受け入れることができるのであれば、それでも構わないということです。
もちろん、何を持って受け入れることが可能なのかどうかは個人にもよりますし、業界や分野によっても違います。そして科学論文の世界では5%を超えるような間違っている確率というのは受け入れらない、逆に5%未満の間違っている確率であれば受け入れられるという暗黙の合意があって、5%が有意水準としてよく使われていると言えるのです。
そしてこれがネイマンによるP値の解釈です。
タイプ1エラーの許容範囲としてP値の有意水準を決めるという話をしてきましたが、タイプ2エラーに関してもその許容範囲を決めたりします。この話は説明しやすくするために、次のt検定の話の後にします。
何が正しいか正しくないかという話はおいておいて、ここで皆さんに理解してほしいのは、こうした統計検定の背景にある考え方です。
どちらの方法も筋は通っているのですが,この両者には仮説検定に対するかなり異なった考え方が反映されています。一般的にはフィッシャー流の考え方がよく使われていますが、帰無仮説検定のロジックがうまく反映されているという点では、ネイマン流の考え方のほうが多くの人にとってわかりやすいかもしれません。
もちろん、どちらがわかりやすいかは人によって違うものです。
P値の間違った解釈
ここまでP値の解釈について話してきましたが、ここでよくあるP値の間違った解釈についても話しておきたいと思います。それは「帰無仮説が正しい確率」または「どれくらい帰無仮説が正しいのか」といった解釈です。直感的にこのように解釈したくなる気持ちは山々なのですが、これは間違った解釈です。
というのも、これは確率論の章でも話しましたがここでの確率とは頻度主義の解釈が取られます。それは何度も繰り返した時に何回起こるかというもので、例えば100回繰り返したらそのうち何回期待した結果が得られるか、といったものです。5%の確率というとき、それはたとえば100回繰り返したら期待した結果が5回得られるという意味です。
このように確率を解釈した上で、得られたP値が有意水準よりも低いか高いかによって帰無仮説を棄却できるかできないか、この2通りの答えしかないのです。もしP値が3%であるならばそれは100回繰り返しても期待した結果が3回しか出ないということであり、有意水準が5%と決められているのであれば有意であるので、帰無仮説を棄却できるということです。
もしネイマン流の解釈を採用したとすると、P値が3%であるということは、有意であると判断した場合に間違ってる確率が3%であり、それは受け入れることができるレベルなのであれば、そのまま有意であると判断し、帰無仮説を棄却することになります。
フィッシャー流でもネイマン流でも、結果は帰無仮説が正しいか(受け入れ続ける)、または間違ってる(棄却する)のどちらか2つしか答えはありません。結果は白黒どちらかないのであり、帰無仮説自身に対してそれが3%くらい正しいといった帰無仮説に対する判断がグレーになることはないのです。
棄却領域
この問題に答えるためには,検定統計量 X の棄却域(危険域)という概念を導入する必要があります。検定の棄却域とは,帰無仮説を棄却すべき X の値を示したものです。この棄却域はどのように求めればよいのでしょうか。
まず,ここまでにわかっていることを整理しましょう。
帰無仮説を棄却するには, X は非常に大きいか非常に小さい必要があります。
帰無仮説が正しいなら, X のサンプル分布は Bin(0.5,N) になります。
もし α=.05 なら,棄却域はこの標本分布の5%の範囲をカバーしなければなりません。
とくに最後の点についてしっかり理解しておいてください。棄却域というのは帰無仮説を棄却する X の値に対応していて,ここで使用している標本分布は,帰無仮説が真である場合に特定の X の値が得られる確率を示しています。ここで,標本分布の20%をカバーするような棄却域を設定したとしましょう。そして帰無仮説が実際に正しかったとします。帰無仮説を誤って棄却する確率はいくつでしょうか。答えはもちろん20%です。この場合, α の水準が 0.2 の検定を行ったことになります。もし α=.05 としたければ,棄却域がカバーすることを許されるのは,検定統計量の標本分布のうち5%だけなのです。
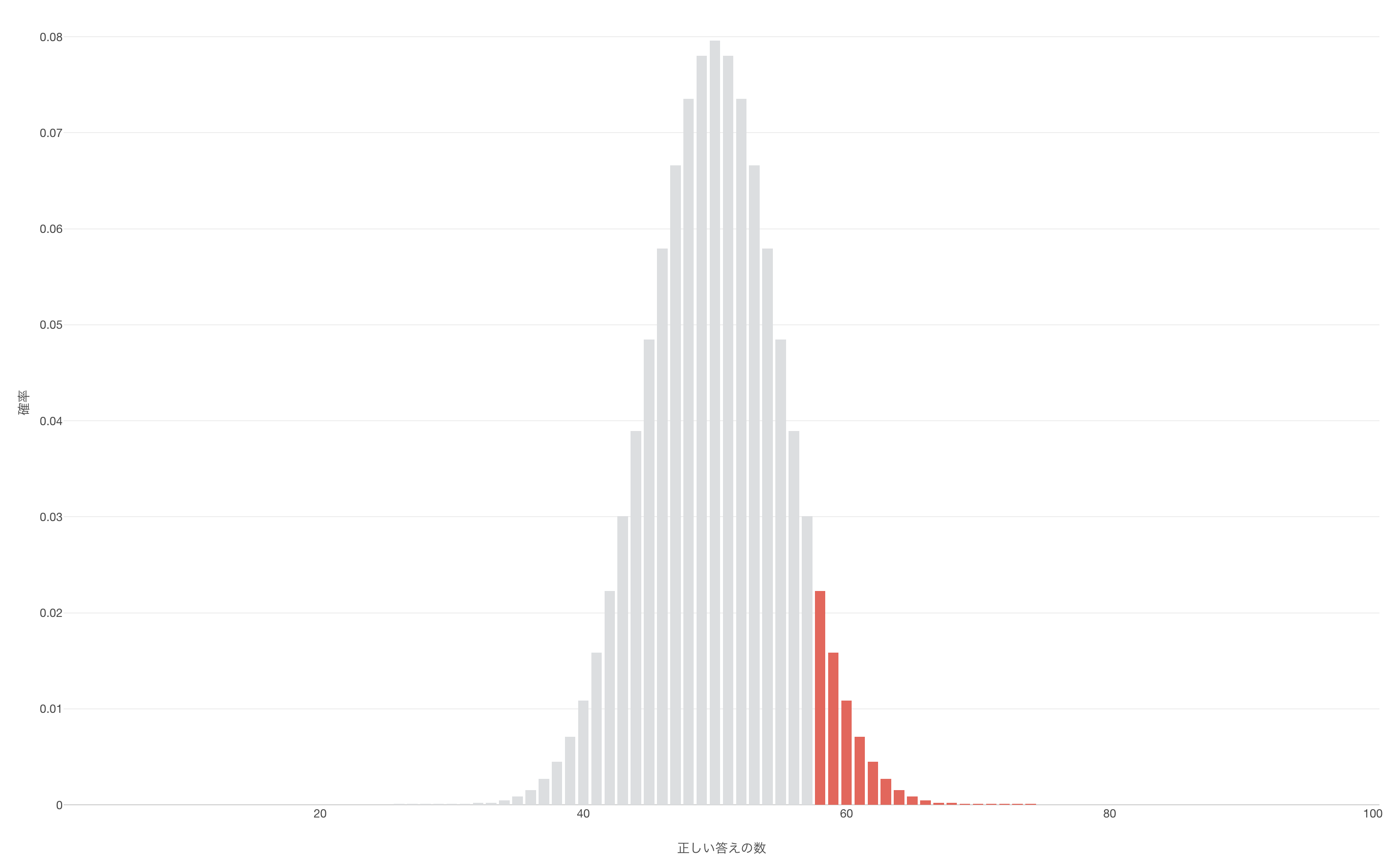
棄却域は非常に極端な値で構成されていて,これは分布の裾と呼ばれます。これを示したのが下の図です。
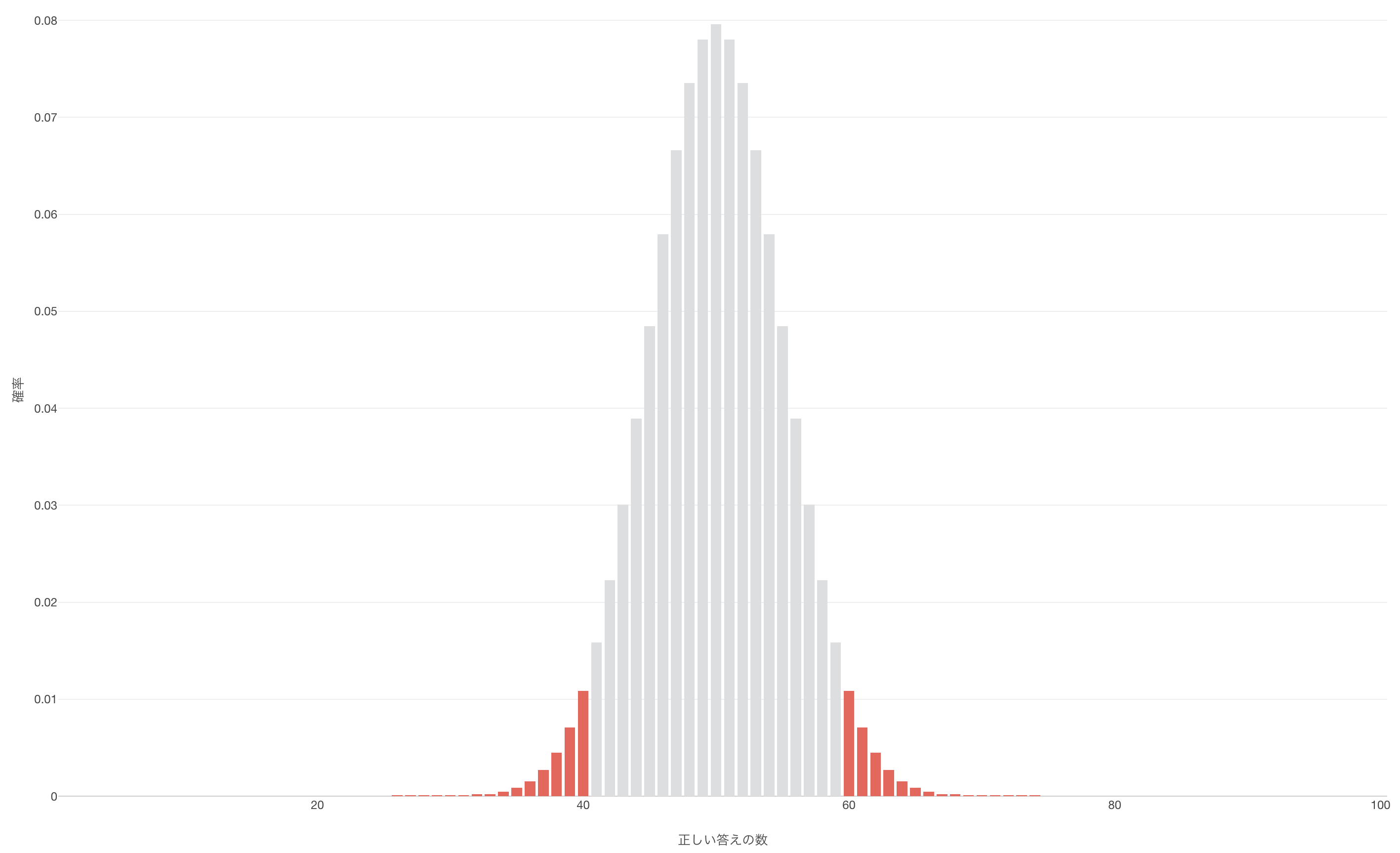
これは上記のチャートと基本的に同じものです。グレーのバーは,帰無仮説を保持するX
の値。青いバーは帰無仮説の棄却域を示します。Xの値が0.5 (50%)
に比べて大きすぎても小さすぎても帰無仮説を棄却するために棄却域は分布の両側の裾となります。もし有意水準を0.05
(5%)
とするのであれば両側のそれぞれの領域は分布全体の2.5%をカバーする必要があります。
この場合、棄却域は Xの値が40以下または60以上となります。つまり,「正答」した回数が41回から59回の間であれば,私たちは帰無仮説を保持すべきということなのです。逆に、もし値が0から40,または60から100ならば,帰無仮説を棄却すべきということになります。なお,この40と60に相当する数値は,棄却域の境目の部分であることから臨界値と呼ばれることもあります。
仮説検定のフレームワーク
- α の水準を選択する(たとえば α=.05 )
- 帰無仮説(H0)と対立仮説(H1)を比較することが可能な何らかの検定統計量を選択する( 10回中何回など)
- 帰無仮説が正しい場合の検定統計量の標本分布を探す(今回の例では二項分布)
- α の水準に適した棄却域を設定する(0-40と60-100)
片側検定と両側検定
これまで見てきたワインテイスティングの例では、帰無仮説はフレデリックは「カリフォルニアとフレンチのワインの違いがわからない」であり、それに対する対立仮説は「カリフォルニアとフレンチのワインの違いがわかる」でした。
この場合私たちはもし帰無仮説が正しいのであれば、10杯中9杯以上当たることはほぼないだろうから、もしフレデリックが9杯当てたのであれば帰無仮説を棄却できるという前提で話を進めてきました。
ここで仮説を整理してみましょう。
私たちの持っている帰無仮説は「違いがわからない」なので、この場合は50%ということが言えます。
そしてその逆の対立仮説は「違いがわかる」なので、私たちはそれは50%以上だろうと想定していたことになります。もちろん現実世界ではばらつきがあるわけですから、帰無仮説が正しければ50%ちょうどになるというわけではありませんし、逆に6回当たったからといって、帰無仮説を棄却できるというわけではありません。棄却できる有意水準を5%としていたのであれば、右側の5%となる領域に入る回数当たっていた時に棄却できるということです。
しかし、もしフレデリックが10杯中1杯しか当てることができなかったとしたらどうでしょうか?
この場合先ほどの確率分を元にした棄却できる領域には入っていないため、有意とはなりません。しかしよく考えてみてください。
もし適当に言っているとして1杯以下、つまり0杯か1杯しか当てることができないというのは、左から見れが、約1%の確率でしか起き得ないことです。
<image>
適当に言っていれば、5杯を前後としてだいたい3杯から7杯くらいの間で当てることができているはずです。それが1杯しか当てられないのだとしたら、それはそれで何か特別な能力があるのかもしれません。もしかしたら、何かの間違いでカリフォルニアとフレンチを言い間違えているだけで、違い自体はわかっているのかもしれません。
ここで問題なのは私たちは帰無仮説を考えるさいに無意識のうちにうまく当てることができるのは50%以下だろうと想定していたということです。そしてそれに伴って対立仮説は50%以上だろうとしていたということです。ですので、この場合当たった回数がどれだけ極端に大きい方の数字が出たのかに注意していました。ですのでこの場合は、たとえ極端な数値だとしてもそれが小さい数値なのであれば、結局違いがわからないという帰無仮説が正しいのだと判断していたことになります。
こういった仮説検定のことを片側検定と呼びます。確率分布の片側だけ、今回であれば大きな数値の方にだけ有意水準をもとにした棄却領域を設定したものです。ですので、もし有意水準が5%なのであれば、右側の極端に大きい数値の方面だけに5%となる領域を設定することになります。
しかし、もしカリフォルニアかフレンチかラベルを当てることはできなかったとしても、コンシステントにふたつのワインの違いを当てることができていたとしても、それをもって帰無仮説である「違いがわからない」を棄却したいのであれば、もし有意水準が5%なのであれば両側を含めた上で全体の5%となるように棄却領域を設定することになります。この場合はそれぞれの側の棄却領域は2.5%となり、足し上げると5%となります。
こうした検定のことを両側検定と呼びます。
目的に応じて片側検定か、両側検定かを使い分けることになるのですが、一般的には両側検定が行われることが多いです。というのも、仮説検定を行う際の主な目的は、手元のデータにおいて見えているものはただのデータのばらつきなのか、そうではないのかを見極めたいことであるからです。もし2つのチームの学校の成績の平均点に違いがあるのであれば、どちらのチームの平均点が大きいかよりも、その違いは十分に大きいと言える違いなのかどうかであるのです。この2つのチームの平均点における違いに関する仮説検定は次のt検定の章で詳しく解説します。
誤りを認めて意見を変える
ここで重要なのは、仮説が間違っているという基準を作ったということです。そして期待、または予測された結果と現実世界での結果が辻褄が合っていないのであれば、その予測を作る元となった仮説を棄却するための基準を作ったということです。
これが仮説検定です。こうして考えると、仮説検定とは意見を変えるための手法とも言えるのでは無いでしょうか。何か自分が思っている、信じていることがあった場合、それは自分の頭の中だけで考えていることかもしれません。または現実世界で観察した結果かもしれませんが、それはたった1人のアメリカ人に出会って、その人が親切だったのでアメリカ人はみんな親切だと思っているのかもしれません。
その頭の中で作り上げた仮説がほんとうに正しいかどうか、現実世界でも十分通用する理論となるのか知りたいですよね。そこでデータを集め、観察もしくは実験をすることになるのですが、その場合にデータのばらつきを考慮した上でもし間違ってたら意見を変えたい、しかし適当には変えたく無い、変えるのであればそれなりの根拠を持って変えたい、そんなときにデータがあれば仮説検定の手法が役に立ちますし、たとえ無かったとしてもこの考え方が自分の仮説がほんとに正しいのか判断し、必要であれば意見を変えることができるようになるのです。
自分の持つ考えや意見を変えるというのは勇気のいるものです。そして謙虚さも必要になります。ビジネスの場面でもそうですが、多くの場合は自分の主張を押し通すことばかりに目が向きがちです。しかし、議論で相手を打ち負かすのはその場は気持ちいいかもしれません。自分が正しかったと思い続けるのは満足のいくものです。
しかし、もし間違っていたとき、それはずっと間違え続けることを意味します。私も自分の会社でみんなを前にして話す時に、昨日まで間違っててもいい、つらいがわかっただけいいではないか。しかし明日からも間違い続けるのはもっとひどい。もし間違いに気づいて、軌道修正することで明日からより良い道を歩いて行けることができるのであれば、明日に希望があるということです。間違っているかもしれないと気づいているが、意見を変えることができなくなって、辻褄を合わせるためにおかしな理論を上塗りしていく、そんな明日は暗いですね。
しかし、これは何も帰納的に考えればそれで十分だというわけではありません。というのも天動説を支持する人たちは、このように反論するかもしれません。
私は毎日太陽の動きを観察しているが、太陽は毎日東から上り、その後空をぐるっと回って最後西に沈む、そしてまた次の朝になると東から上ってくる。私は理論的に言っているわけではなく、観察を元に、つまり帰納的にこういう結論に達したのだ、という具合にです。
この問題はただ観察することから始めた、または太陽が動くという仮説から始めたから問題なのです。もし地球が動くという仮説から始めたらどうでしょうか。その場合、地球が自転しているという仮説から始めるということですが、その場合ただ単に太陽の動きを毎日観察していても始まりません。地球が自転していてもおかしくないという